本文前置知识:
Back to Basics: Let Denoising Generative Models Denoise
- 论文: Back to Basics: Let Denoising Generative Models Denoise.
- 代码: GitHub - LTH14/JiT: PyTorch implementation of JiT https://arxiv.org/abs/2511.13720.
Basic Idea
根据流形假设, 自然图像$\boldsymbol{x}$ 是位于高维空间中的低维流形上, 但是噪声$\boldsymbol{\epsilon}$ 是随机分布的, 不会散落在流形上. 由于速度$\boldsymbol{v}$ 一般由$\boldsymbol{x}$ 和 $\boldsymbol{\epsilon}$ 计算得到, 所以模型预测的$\boldsymbol{v}$ 也是流形外的:
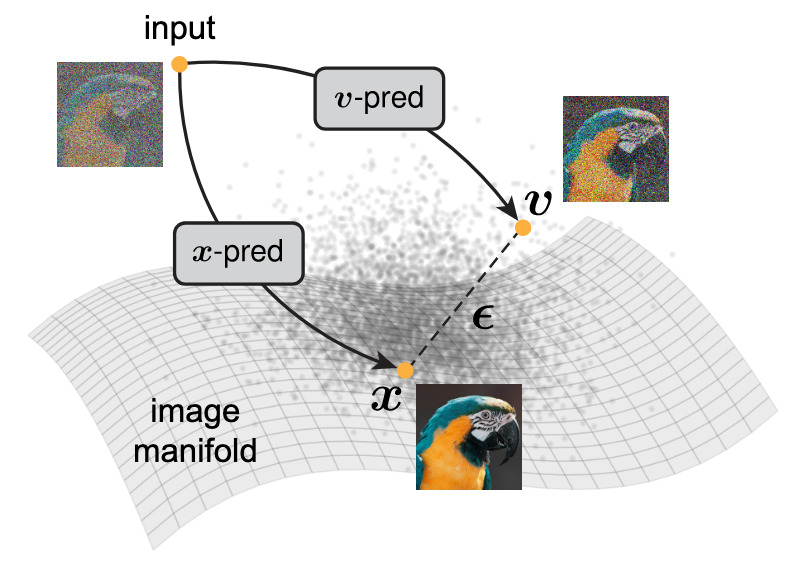
本文JiT(Just image Transformers), 认为直接预测$\boldsymbol{x}$ 比预测$\boldsymbol{v}, \boldsymbol{\epsilon}$ 要好. 基于流形假设, 预测自然图像$\boldsymbol{x}$ 的难度比预测速度$\boldsymbol{v}$ 或者噪声$\boldsymbol{\epsilon}$ 都要低.
之前相当多的工作中探讨过这个问题, 普遍认为$\boldsymbol{x}$ 要更加难以预测. 所以大多数工作才将预测放在Latent Space里面, 做$\boldsymbol{\epsilon}, \boldsymbol{v}$-pred.
On Prediction Outputs of Diffusion Models
Background: Diffusion and Flows
没有基础的可以看Rectified Flow / Flow Matching.
假设数据分布$\boldsymbol{x} \sim p_\text{data}(\boldsymbol{x})$, 噪声分布$\boldsymbol{\epsilon} \sim p_{\text{noise}}(\boldsymbol{\epsilon})$, 为先验分布, 例如$\boldsymbol{\epsilon} \sim \mathcal{N}(0, \boldsymbol{I})$. 训练阶段用线性插值采样一个含噪样本$\boldsymbol{z}_t = a_t \boldsymbol{x} + b_t \boldsymbol{\epsilon}$, 一般直接采用线性调度, $a_t=t, b_t=1-t$, 可得:
$$
\boldsymbol{z}_t=t \boldsymbol{x}+(1-t) \boldsymbol{\epsilon}
$$
当$t=1$ 时有$\boldsymbol{z}_t \sim p_{\text{data}}$. 同时令$\text{logit}(t) \sim \mathcal{N}(\mu, \sigma^2)$.
速度场$\boldsymbol{v}$ 定义为$\boldsymbol{z}$ 的时间导数, 即$\boldsymbol{v}_t = \boldsymbol{z}^\prime_t = a_t^\prime\boldsymbol{x} + b_t^\prime\boldsymbol{\epsilon}$, 根据$\boldsymbol{z}_t$, 有:
$$
\boldsymbol{v}=\boldsymbol{x} - \boldsymbol{\epsilon}
$$
Flow-based方法直接将速度$\boldsymbol{v}_\theta$ 直接由参数化网络$\theta$ 得到, 即$\boldsymbol{v}_\theta=\text{net}_\theta(\boldsymbol{z}_t, t)$, 然后计算网络预测的速度场和真实速度场之间的MSE:
$$
\mathcal{L}=\mathbb{E}_{t, \boldsymbol{x}, \boldsymbol{\epsilon}}\left\Vert\boldsymbol{v}_\theta\left(\boldsymbol{z}_t, t\right)-\boldsymbol{v}\right\Vert^2
$$
因此, 采样可以通过求解ODE完成:
$$
d \boldsymbol{z}_{t} / dt = \boldsymbol{v}_\theta (\boldsymbol{z}_t, t)
$$
从$\boldsymbol{z}_0 \sim p_{\text{noise}}$ 开始, 并从$t=1$ 结束.
Prediction Space and Loss Space
Prediction Space
网络啥都能学, 预测$\boldsymbol{x}, \boldsymbol{v}, \boldsymbol{\epsilon}$ 都可以, 也就是网络的Prediction Space. 对于网络预测的任意一项已知量, 可以通过附加两个额外约束来推导所有的三项未知量. 例如, 当网络预测$\boldsymbol{x}$ 时, 有:
$$
\left\{\begin{array}{l}
\boldsymbol{x}_\theta=\text {net}_\theta \\
\boldsymbol{z}_t=t \boldsymbol{x}_\theta+(1-t) \boldsymbol{\epsilon}_\theta \\
\boldsymbol{v}_\theta=\boldsymbol{x}_\theta-\boldsymbol{\epsilon}_\theta
\end{array}\right.
$$
可以求解得到$\boldsymbol{\epsilon}_\theta=(\boldsymbol{z}_t-t \boldsymbol{x}_\theta) / (1-t), \boldsymbol{v}_\theta=(\boldsymbol{x}_\theta- \boldsymbol{z}_t) / (1-t)$.
Loss Space
由于所有量都可以通过网络预测推导而得, 所以网络即使预测$\boldsymbol{x}$ 也不一定非要计算$\boldsymbol{x}$ 的loss, 比如可以预测$\boldsymbol{x}$ 但是通过推导得到$\boldsymbol{v}$, 然后计算$\boldsymbol{v}$ 的loss, 这就是Loss Space.
综上, 作者对预测什么(Prediction Space), 用什么算Loss(Loss Space)做了个穷举:
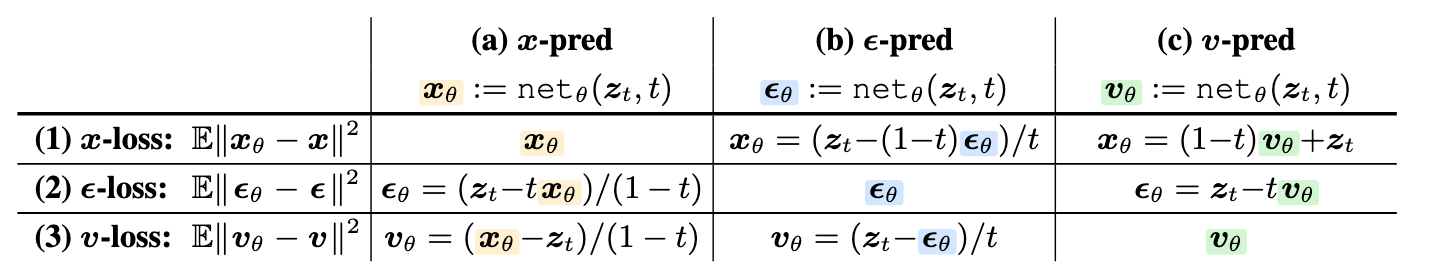
虽然它们从公式上来说是可以互相推出来的, 但是网络每次学起来迭代的时候, 难易程度是不一样的.
主对角线其实代表了三大经典模型:
- $\boldsymbol{x}$-pred & $\boldsymbol{x}$-loss: 早期所有直接预测原图, 并在原图上算Loss的模型(在Diffusion时代之前的模型大多为这种).
- $\boldsymbol{\epsilon}$-pred & $\boldsymbol{\epsilon}$-loss: DDPM这类以预测噪声为目标并优化的模型.
- $\boldsymbol{v}$-pred & $\boldsymbol{v}$-loss: Flow Matching / Rectified Flow这种以学习速度场为目标的生成类模型.
但是不管pred / loss怎么组合, 训练完成后的推理的时候在 $\boldsymbol{x} / \boldsymbol{\epsilon} / \boldsymbol{v}$ 上做都可以, 此时称为Generator Space. 遵循Flow-based Model求解ODE的习俗, 在$\boldsymbol{v}$ 上做推理采样.
Toy Experiment
作者希望在Toy Dataset上验证前文的低维流形假设. 令模型分别生成$\boldsymbol{x}, \boldsymbol{v}, \boldsymbol{\epsilon}$, 观察模型生成哪种量最简单.
具体的, 将低维流形$\hat{\boldsymbol{x}} \in \mathbb{R}^d$ 通过固定随机列正交矩阵$P \in \mathbb{R}^{D \times d}$ 嵌入到更高维的空间$D$ 中, 即将其转换为高维观测数据$\boldsymbol{x} = P \hat{\boldsymbol{x}}$, 然后让模型在未知$P$ 的情况下用$\boldsymbol{x}$ 生成$\hat{\boldsymbol{x}}$.
模型用的是5层ReLU激活的MLP, hidden size为256, 均采用$\boldsymbol{v}$-loss进行训练, 结果如下:
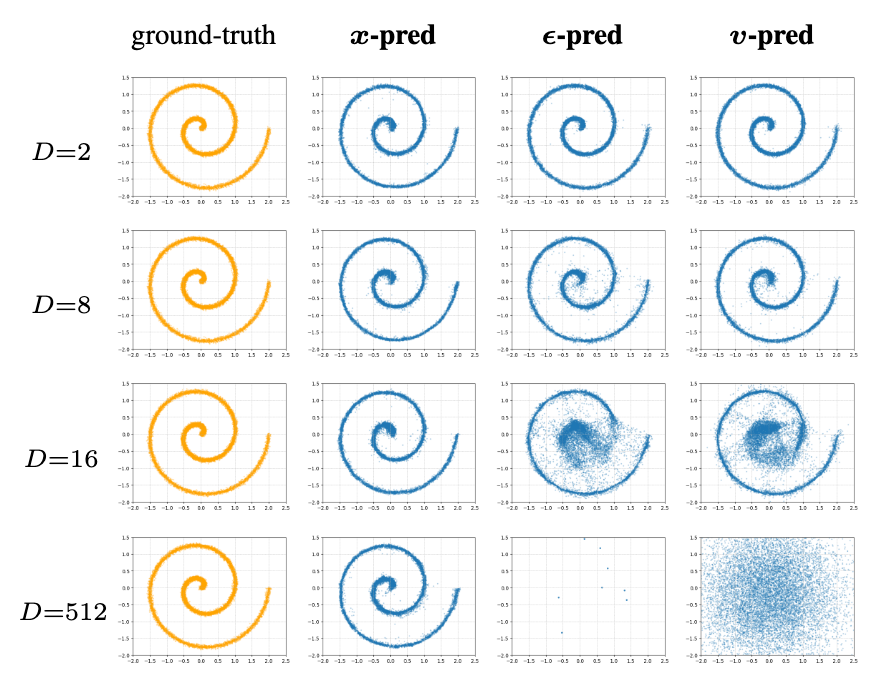
在所有$D$ 的设置下, $\boldsymbol{x}$-pred在降回到二维的时候, 仍然能保持住二维流形结构. 并且当$D=512$ 时(即$D$ 比MLP的hidden size大的时候), 其余两种方法出现了崩溃, 在二维空间中无法还原二维流形. 说明$\boldsymbol{x}$ 确实更有可能位于低维流形上, 因此生成起来要更容易.
这个Toy Experiment说明JiT具有应用到更大Patch, 或者具有更高维数据的潜力.
“Just Image Transformers” for Diffusion
Just Image Transformers
JiT Overview确实就是一个Image Transformer:
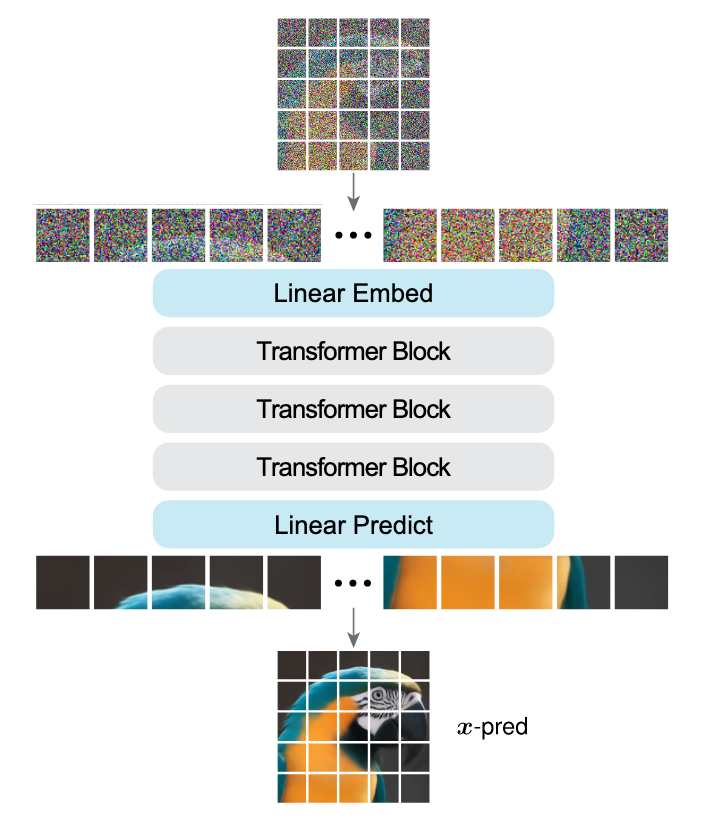
- Linear Embed: 构造一个低维的Bottleneck(例如128, 256, 具体大小视数据集大小而定), 将原始数据直接压缩到一个低维流形中, 然后将低维流形的数据投影到Trm Block(DiT Block)的Hidden Size.
- 将Embedding输入到串行的Trm Block中计算.
- Linear Predict: 只是一层Linear, 直接从Hidden Size投影到像素域.
- 但是和其他生成类模型不同的是, JiT学习到的是预测像素域的值$\boldsymbol{x}$, 而不是噪声$\boldsymbol{\epsilon}$, 也不是速度$\boldsymbol{v}$.
What to Predict by the Network?
x-prediction is critical
作者在九宫格设置上进行了实验, 结果如下, 红色代表崩溃:
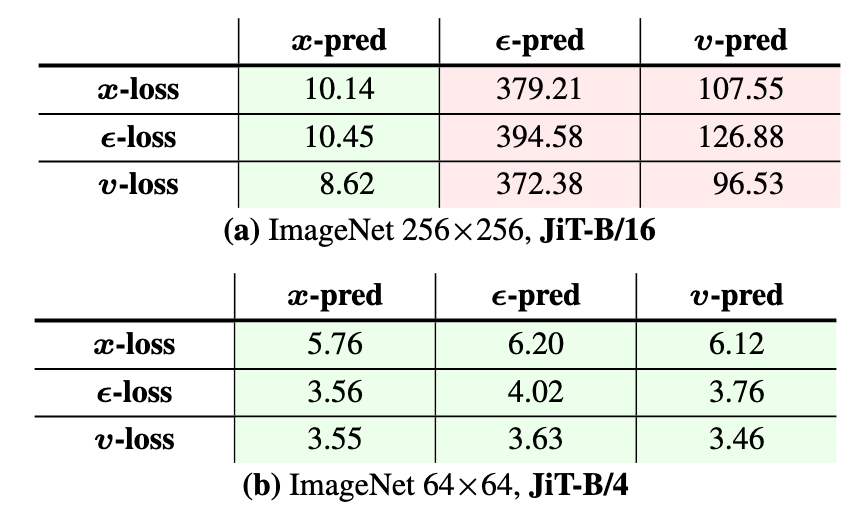
- Patch size为4时: 对应的像素域维度为$4^2\times3=48$, 所有方法都可以在ImageNet 64×64上做Work, 各种方法差距不大. 此时JiT-B的Hidden size远大于像素空间维度.
- Patch size为16时: 只有$\boldsymbol{x}$-pred是可以做Work的. 对应的像素空间维度为$16^2\times3 = 768$, 恰和JiT-B的Hidden size相同. 说明JiT的方法比其他方法有更强面对高维输入的处理能力.
同时, 可以观察到$\boldsymbol{v}$-loss的表现比其他两种要好, 所以可以采用$\boldsymbol{v}$-loss进行训练.
这个结论比较关键, 说明$\boldsymbol{\epsilon}, \boldsymbol{v}$ 在空间中确实不符合流形假设, 相较于$\boldsymbol{x}$ 的建模需要更高的Hidden size.
Noise-level shift is not sufficient
之前有一些方法建议采用Logit-Normal来采样$t$, 通过调整$\mu$ 来调整噪声的水平. 作者探究了不同噪声水平对三种pred方式的影响:
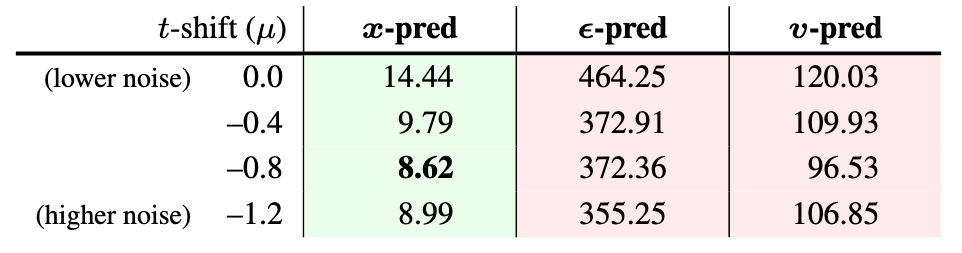
$\boldsymbol{x}$-pred可以从适当增加噪声中受益, 但通过调整噪声水平无法挽救$\boldsymbol{\epsilon}, \boldsymbol{v}$-pred的崩溃问题.
Bottleneck can be beneficial
基于低维流形假设, 作者显式的构造了Bottleneck, 然后进行了不同维度Bottleneck对结果的影响:
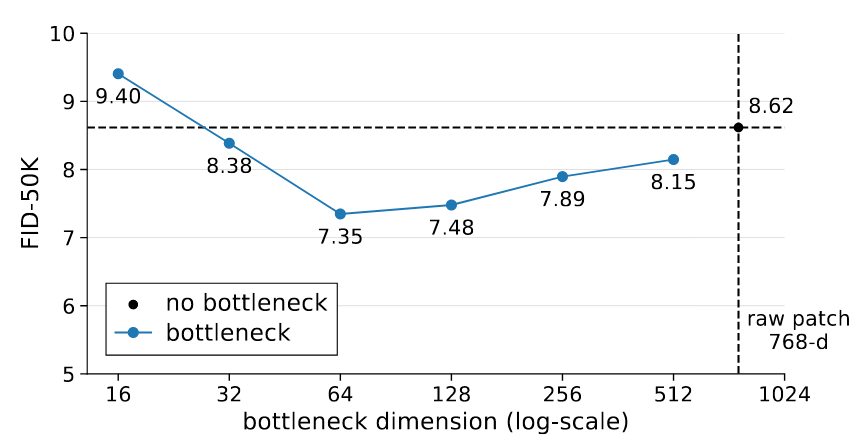
构造Bottleneck有利于提高生成表现, 维度适当的时候, 还可以提升模型性能. 当Bottleneck过小的时候也不会导致模型崩溃.
JiT’s Algorithm
因此, JiT的核心贡献, 就是下面这个由$\boldsymbol{x}$-pred推出来的$\boldsymbol{v}$-loss:
$$
\begin{aligned}
\mathcal{L}&=\mathbb{E}_{t, \boldsymbol{x}, \boldsymbol{\epsilon}}\left\Vert\boldsymbol{v}_\theta\left(\boldsymbol{z}_t, t\right)-\boldsymbol{v}\right\Vert^2 \\
\boldsymbol{v}_\theta\left(\boldsymbol{z}_t, t\right)&=\left(\operatorname{net}_\theta\left(\boldsymbol{z}_t, t\right)-\boldsymbol{z}_t\right) /(1-t)
\end{aligned}
$$
因为计算$\boldsymbol{v}_\theta(\boldsymbol{z}_t, t)$ 需要除$1-t$, 避免零除, 所以将$1-t$ 的最小值裁剪到0.05.
训练 / 采样推理伪代码如下:

- 在Training的时候, 用模型预测
x_pred, 并通过公式计算得到v_pred, 将v_pred用于$\boldsymbol{v}$-loss的计算. - 在Inference的时候, 仍然用
x_pred计算得到v_pred, 完成欧拉采样. JiT在论文中采用的实际上是Heun而不是Euler.
“Just Advanced” Transformers
JiT里也使用了一些其他工作已经验证有效的方法来加速收敛. 例如SwiGLU, RMSNorm, RoPE, QKNorm等. 下面是提升:

Comparisons
下面是一些消融 / 包含比较的实验.
High-resolution generation on pixels
作者在不同分辨率的ImageNet上, 用相同规模的JiT和不同的Patch size进行了实验:

作者发现, JiT的Patch size设置可以随分辨率提升而扩大, 且同时完全不提升Token数量和Backbone参数量. 当Patch size开到32 / 64的时候, 像素空间维度为3072 / 12288, JiT-B仍然能正常工作.
这种特性可以显著节省高分辨率图像生成时候的计算成本.
此外, 从现象可以认为, JiT很大程度上可以与观测维度解耦, 所以JiT架构的Scaling增大模型的Hidden size可能也不是必须的.
Scalability
作者测试了JiT架构的Scaling能力:

除了越大效果越好外, 在JiT-G上的512×512甚至超过了256×256的性能.
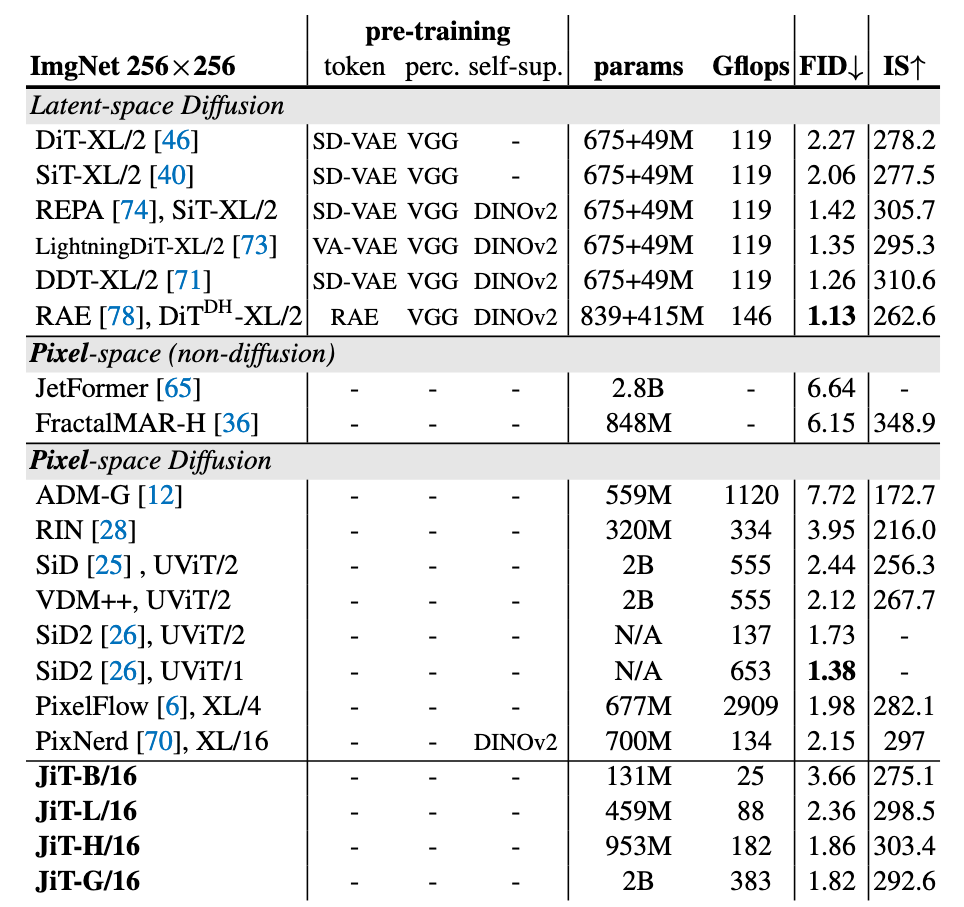
Reference results from previous works
ImageNet 256×256上的结果:
ImageNet 512×512上的结果:
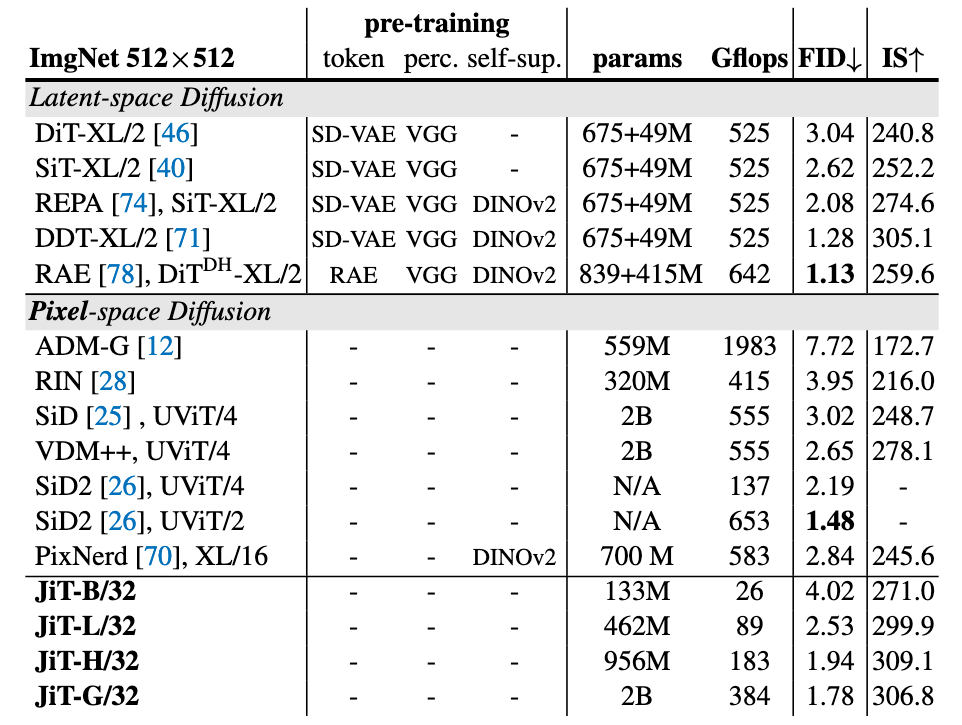
JiT的优势主要体现在计算量上要大大少于先前的模型, 却拥有差不多的生成质量.
Summary
JiT是一篇争议比较大的论文, 自从它挂在Arxiv上, 知乎争论就不断. 因为它重新在Pixel Space上进行学习, 与目前用Pretrained-VAE在Latent Space上做生成的主流认知是相悖的. 能打破大家的思维定式就是一篇好文章, 无关故事讲的好不好.
早期的DiT之类的工作试过在Latent Space上做大Patch Diffusion, 但是失败了. JiT能Work, 可能说明目前模型的生成质量上限受制于VAE-Decoder, 同时也不需要Tokenizer了.
性能角度上来说, JiT取得了和其他$\boldsymbol{\epsilon}, \boldsymbol{v}$-pred的SOTA方法Comparable的结果. 但是它还是一个非常年轻的框架, 所以还有很大的改进空间.
个人比较看好的是, 它具有在大Patch / 高维度数据上建模的潜力, 而且不过多引入额外的计算成本, 包括但不限于各类模态 / 领域数据.
推荐继续阅读:

