RoPE / RoFormer: Enhanced Transformer with Rotary Position Embedding
本文是论文 RoFormer: Enhanced Transformer with Rotary Position Embedding 的阅读笔记和个人理解.
Recommended
与往常不同, 在本文开头先给出推荐.
首先苏神博客看RoPE整个系列的文章(RoPE的论文就是出自这些博客的集成):
- 让研究人员绞尽脑汁的Transformer位置编码 - 科学空间|Scientific Spaces.
- Transformer升级之路:2、博采众长的旋转式位置编码 - 科学空间|Scientific Spaces.
- 标签 rope 下的文章 - 科学空间|Scientific Spaces.
本文中穿插的内容也有少量由苏神博客中延伸.
如果想看比较简单一点的, 强烈推荐直接看抱抱脸推出的Blog设计位置编码, 从一个比较简单易懂的角度解释了RoPE的由来.
代码方面, 也推荐看看LLaMA对RoPE的实现:
如果希望看形象一点的, 有图描述的, 推荐看:
本文是对RoPE论文的记录.
Background and Related Work
位置编码的主要作用是为了保证同样的Token输入到模型中是可以区分的, 从而可以编码它们的位置关系. 一个显然的例子, “我吃饭”和”饭吃我”明显因主宾语的位置不同而具有不同的含义.
熟悉的Position Embedding的本小节可以跳过.
Preliminary
对于长度为$N$ 的句子$\mathbb{S}_N$ , 将其中所有Token组成的Embedding序列$\mathbb{E}_N$, $\boldsymbol{x}_i \in \mathbb{R}^d$ 为$\mathbb{E}_N$ 中第$i$ 个位置上的$d$ 维Embedding.
当Transformer中的Self - Attention在忽略位置信息的情况下, 其Attention Score的计算方式如下:
$$
\begin{aligned}
\boldsymbol{q}_m & =f_q\left(\boldsymbol{x}_m, m\right) \\
\boldsymbol{k}_n & =f_k\left(\boldsymbol{x}_n, n\right) \\
\boldsymbol{v}_n & =f_v\left(\boldsymbol{x}_n, n\right)
\end{aligned}
$$
其中$\boldsymbol{q}_m$, $\boldsymbol{k}_n, \boldsymbol{v}_n$ 分别为第$m, n$ 位置通过$f_q, f_k, f_v$ 获得的Query, Key, Value.
接着计算Scaled Dot-Product Attention:
$$
\begin{aligned}
a_{m, n} & =\frac{\exp \left(\frac{\boldsymbol{q}_m^{\top} \boldsymbol{k}_n}{\sqrt{d}}\right)}{\sum_{j=1}^N \exp \left(\frac{\boldsymbol{q}_m^{\top} \boldsymbol{k}_j}{\sqrt{d}}\right)} \\
\mathbf{o}_m & =\sum_{n=1}^N a_{m, n} \boldsymbol{v}_n
\end{aligned}
$$
$a_{m, n}$ 为$m, n$ Token之间的Attention Score, $\mathbf{o}_m$为第$m$ 个Token的计算完Self - Attention后的表示.
Absolute Position Embedding
最经典的$f_{t: t \in\{q, k, v\}}(\cdot)$ 的方法是直接将Embedding $\boldsymbol{x}_i$ 与位置信息$\boldsymbol{p}_i$ 直接相加, 再通过一个线性投影$\boldsymbol{W}_{t: t \in\{q, k, v\}}$ 直接得到:
$$
f_{t: t \in\{q, k, v\}}\left(\boldsymbol{x}_i, i\right):=\boldsymbol{W}_{t: t \in\{q, k, v\}}\left(\boldsymbol{x}_i+\boldsymbol{p}_i\right)
$$
而在Transformer的原论文中, 作者通过正余弦函数来生成$\boldsymbol{p}_i$:
$$
\begin{cases}\boldsymbol{p}_{i, 2 t} & =\sin \left(k / 10000^{2 t / d}\right) \\\ \boldsymbol{p}_{i, 2 t+1} & =\cos \left(k / 10000^{2 t / d}\right)\end{cases}
$$
$\boldsymbol{p}_{i, 2 t}, \boldsymbol{p}_{i, 2 t+1}$ 分别为$\boldsymbol{p}_i \in \mathbb{R}^d$ 的奇数维和偶数维.
当然, 在BERT, ViT等论文中也有直接使用Learnable的绝对位置编码, 直接将绝对位置设定为一个可学习的参数让网络自己学.
Relative Position Embedding
由于绝对位置编码不能编码两个Token之间的相对位置关系, 一些工作中也通过相对位置的建模, 将相对位置信息作为位置编码:
$$
\begin{aligned}
f_q\left(\boldsymbol{x}_m\right)&:=\boldsymbol{W}_q \boldsymbol{x}_m \\
f_k\left(\boldsymbol{x}_n, n\right)&:=\boldsymbol{W}_k\left(\boldsymbol{x}_n+\tilde{\boldsymbol{p}}_r^k\right) \\
f_v\left(\boldsymbol{x}_n, n\right)&:=\boldsymbol{W}_v\left(\boldsymbol{x}_n+\tilde{\boldsymbol{p}}_r^v\right)
\end{aligned}
$$
$\tilde{\boldsymbol{p}}_r^k, \tilde{\boldsymbol{p}}_r^v \in \mathbb{R}^d$ 为可学习的相对位置编码.
其中, $r$ 为$m, n$ 之间的相对位置, 用$r=\text{clip}(m-n, r_{min}, r_{max})$ 得到. 这假设了超出一定距离限制的位置信息是不太重要的. 此时直接采用最远距离的相对位置编码即可.
一些工作(TransformerXL / XLNet)直接沿用这个形式将它们按项拆分:
$$
\boldsymbol{q}_m^{\top} \boldsymbol{k}_n=\boldsymbol{x}_m^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{x}_n+\boldsymbol{x}_m^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{p}_n+\boldsymbol{p}_m^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{x}_n+\boldsymbol{p}_m^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{p}_n
$$
进一步的, 由于投影矩阵 $\boldsymbol{W}_k$ 有时候会对Content-based Key $\boldsymbol{x}_n$ 做投影, 有时候会对Position-based Key $\boldsymbol{p}_n$ 做投影, 这显然不合理对吧? 所以可以额外加一个矩阵$\widetilde{\boldsymbol{W}}_k$ 让它来编码$\boldsymbol{p}_n$:
$$
\boldsymbol{q}_m^{\top} \boldsymbol{k}_n=\boldsymbol{x}_m^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{x}_n+\boldsymbol{x}_m^{\top} \boldsymbol{W}_q^{\top} \widetilde{\boldsymbol{W}}_k \tilde{\boldsymbol{p}}_{m-n}+\mathbf{u}^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{x}_n+\mathbf{v}^{\top} \boldsymbol{W}_q^{\top} \widetilde{\boldsymbol{W}}_k \tilde{\boldsymbol{p}}_{m-n}
$$
这玩意看起来太麻烦了, 我们要的其实不就是一项位置信息和一项内容信息吗? 于是一些工作(T5)直接将位置信息和内容信息解耦, 直接将相对位置变为一个Learnable bias term $b_{i, j}$:
$$
\boldsymbol{q}_m^{\top} \boldsymbol{k}_n=\boldsymbol{x}_m^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{x}_n+b_{i, j}
$$
用两个Projection进一步分别编码$\boldsymbol{p}_m, \boldsymbol{p}_n$, 即相对位置, 似乎是更合理的:
$$
\boldsymbol{q}_m^{\top} \boldsymbol{k}_n=\boldsymbol{x}_m^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{x}_n+\boldsymbol{p}_m^{\top} \mathbf{U}_q^{\top} \mathbf{U}_k \boldsymbol{p}_n+b_{i, j}
$$
也有一些工作(DeBERTa)基于绝对位置的形式, 认为简单的将绝对位置$\boldsymbol{p}_n, \boldsymbol{p}_m$ 替换为相对位置$\tilde{\boldsymbol{p}}_{m-n}$就可以:
$$
\boldsymbol{q}_m^{\top} \boldsymbol{k}_n=\boldsymbol{x}_m^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{x}_n+\boldsymbol{x}_m^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \tilde{\boldsymbol{p}}_{m-n}+\tilde{\boldsymbol{p}}_{m-n}^{\top} \boldsymbol{W}_q^{\top} \boldsymbol{W}_k \boldsymbol{x}_n
$$
RoPE
用下图可以概括RoPE的核心思想:
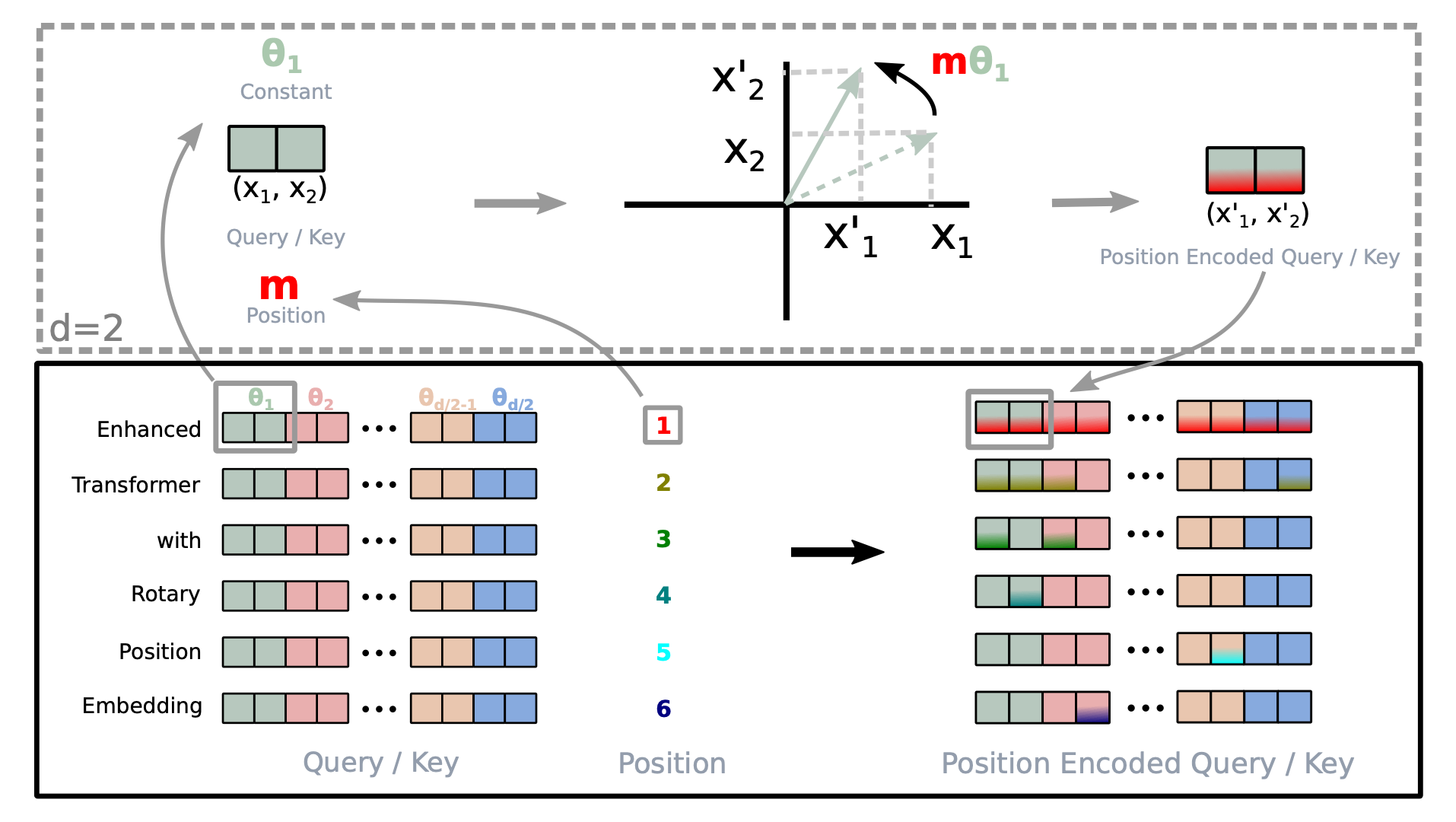
为什么要叫Rotary Position Embedding呢? 正如它的名字一样, 它是通过旋转来区分不同位置的. 上图举了一个$d=2$ 时的简单例子, 对于绝对位置$m$, RoPE将向量在极坐标系中通过旋转能够代表$m$ 的角度来表征它们的位置.
但RoPE是以表征相对位置闻名的, 因为它可以借助一些巧妙的性质, 使得计算Self-Attention的内积时能将相对位置信息注入到其中. 下面就来看看RoPE是怎么做到这一点的.
Formulation
结合前面的分析可知, 想要融入Token之间的相对位置关系, 只需要将$\boldsymbol{q}_m^{\top} \boldsymbol{k}_n$ 建模为能注入相对位置$m-n$ 的函数$g$:
$$
\langle f_q(\boldsymbol{x}_m, m),f_k(\boldsymbol{x}_n, n)\rangle=g(\boldsymbol{x}_m,\boldsymbol{x}_n,m-n)
$$
所以目标就是找到满足$g$ 性质的$f_q(\boldsymbol{x}_m, m),f_k(\boldsymbol{x}_n, n)$.
Rotary Position Embedding
Derivation of RoPE under 2D
在本节中先讨论简单的二维情况.
SDPA(Scaled Dot-Product Attention)是两向量的内积.
如果实数运算规则不好找到函数$g$, 有没有其他的运算规则能帮助我们求解? 比如思考实数内积与复数内积有什么关系吗? 刚刚好, 两向量的内积等于一个复数与另一个复数的共轭的乘积的实部.
例如, 对于任意两个实数向量$\mathbf{a} = (a_1, a_2), \mathbf{b} = (b_1, b_2)$, 它们的内积定义为:
$$
\langle \mathbf{a} \cdot \mathbf{b} \rangle = a_1b_1 + a_2b_2
$$
当我们将$\mathbf{a}, \mathbf{b}$ 看成复数时, 有复数$z_a = a_1 + a_2i$, 其共轭为$z_a^\ast = a_1 - a_2i$, 同理对于复数$z_b = b_1 + b_2i$ 有共轭$z_b^\ast = b_1 - b_2i$. 什么叫”求一个复数与另一个复数的共轭的乘积的实部”? 计算$z_a, z_b^\ast$ 之间的内积:
$$
\begin{aligned}
z_a \cdot z_b^\ast &= (a_1 + a_2i)(b_1 - b_2i) \\
&= a_1b_1 + a_1(-b_2i) + a_2i b_1 + a_2i (-b_2i) \\
&= a_1b_1 + a_2b_2 + i(a_2b_1 - a_1b_2)
\end{aligned}
$$
实部$a_1b_1 + a_2b_2$ 恰好就是$\mathbf{a}, \mathbf{b}$ 在实数域内积的值.
好, 有了上面的性质, 下面开始今天的正题. 先往上小节说的Formulation上靠拢呗.
如果想要表征绝对位置信息, 需要使得$\boldsymbol{q}_m, \boldsymbol{k}_n$ 仅依赖于它们的绝对位置$m, n$:
$$
\begin{aligned}
\boldsymbol{q}_m &= f_q(\boldsymbol{x}_q, m) \\
\boldsymbol{k}_n &= f_k(\boldsymbol{x}_k, n)
\end{aligned}
$$
利用实数内积与复数内积的关联, 我们假设有利用复数运算的函数$g$ 能够在二者做内积的时候编码它们的相对位置关系, 使得其内积依赖于相对位置$m-n$, 以此在内积上表征二者的相对位置信息:
$$
\boldsymbol{q}^\intercal_m\boldsymbol{k}_n = \langle f_q(\boldsymbol{x}_m, m),f_k(\boldsymbol{x}_n, n)\rangle= g(\boldsymbol{x}_m, \boldsymbol{x}_n, n - m)
$$
同时, 这种编码方式还应该保证在初始状态下不编码位置信息:
$$
\begin{aligned}
\boldsymbol{q} &= f_q(\boldsymbol{x}_q, 0) \\
\boldsymbol{k} &= f_k(\boldsymbol{x}_k, 0)
\end{aligned}
$$
首先, 用复数的指数形式(都学过极坐标系中表示复数吧), 将$f_q(\boldsymbol{x}_m, m),f_k(\boldsymbol{x}_n, n)$ 表征为:
$$
\begin{aligned}
f_q(\boldsymbol{x}_q, m) &= R_q(\boldsymbol{x}_q, m)e^{i\Theta_q(\boldsymbol{x}_q, m)} \\
f_k(\boldsymbol{x}_k, n) &= R_k(\boldsymbol{x}_k, n)e^{i\Theta_k(\boldsymbol{x}_k, n)} \\
g(\boldsymbol{x}_q, \boldsymbol{x}_k, n - m) &= R_g(\boldsymbol{x}_q, \boldsymbol{x}_k, n - m)e^{i\Theta_g(\boldsymbol{x}_q, \boldsymbol{x}_k, n - m)}
\end{aligned}
$$
其中, $R_f, R_g, \Theta_f, \Theta_g$ 分别为$f_{\{q, k\}}$ 和$g$ 的幅度(模)和角度. $f$ 的意思是$f_{\{q, k\}}$, 代表$q, k$.
不难发现, 代入到$\boldsymbol{q}_m, \boldsymbol{k}_n$ 中, 当二者做内积时, 得到幅度$R$ 和角度$\Theta$ 之间的关系:
$$
\begin{aligned}
R_q(\boldsymbol{x}_q, m)R_k(\boldsymbol{x}_k, n) &= R_g(\boldsymbol{x}_q, \boldsymbol{x}_k, n - m) \\
\Theta_k(\boldsymbol{x}_k, n) - \Theta_q(\boldsymbol{x}_q, m) &= \Theta_g(\boldsymbol{x}_q, \boldsymbol{x}_k, n - m)
\end{aligned}
$$
此时, 它在初始条件(看成是不表征位置信息)的情况下, 应满足:
$$
\begin{aligned}
\boldsymbol{q} &= \Vert \boldsymbol{q}\Vert e^{i\theta_q} = R_q(\boldsymbol{x}_q, 0)e^{i\Theta_q(\boldsymbol{x}_q, 0)}\\
\boldsymbol{k} & = \Vert \boldsymbol{k}\Vert e^{i\theta_k} = R_k(\boldsymbol{x}_k, 0)e^{i\Theta_k(\boldsymbol{x}_k, 0)}
\end{aligned}
$$
其中, $\Vert q \Vert , \Vert k \Vert$ 和$\theta_q, \theta_k$ 分别为$\boldsymbol{q}, \boldsymbol{k}$ 在二维平面上的幅值(模)和角度.
接着将相同的位置$m=n$ 带入到幅度$R$ 和角度$\Theta$ 的关系式中, 分别得到:
$$
\begin{aligned}
R_q(\boldsymbol{x}_q, m)R_k(\boldsymbol{x}_k, m) &= R_g(\boldsymbol{x}_q, \boldsymbol{x}_k, 0) = R_q(\boldsymbol{x}_q, 0)R_k(\boldsymbol{x}_k, 0) = \Vert \boldsymbol{q}\Vert \Vert \boldsymbol{k}\Vert \\
\Theta_k(\boldsymbol{x}_k, m) - \Theta_q(\boldsymbol{x}_q, m) &= \Theta_g(\boldsymbol{x}_q, \boldsymbol{x}_k, 0) =\Theta_k(\boldsymbol{x}_k, 0) - \Theta_q(\boldsymbol{x}_q, 0) = \theta_k - \theta_q
\end{aligned}
$$
此时, 幅值$R_f$ 的一个显然解为:
$$
\begin{aligned}
R_q(\boldsymbol{x}_q, m) &= R_q(\boldsymbol{x}_q, 0) = \Vert \boldsymbol{q}\Vert \\
R_k(\boldsymbol{x}_k, n) &= R_k(\boldsymbol{x}_k, 0) = \Vert \boldsymbol{k}\Vert \\
R_g(\boldsymbol{x}_q, \boldsymbol{x}_k, n - m) &= R_g(\boldsymbol{x}_q, \boldsymbol{x}_k, 0) = \Vert \boldsymbol{q}\Vert \Vert \boldsymbol{k}\Vert
\end{aligned}
$$
它显然不依赖位置信息, 即满足$\boldsymbol{q} = f_q(\boldsymbol{x}_q, 0), \boldsymbol{k} = f_k(\boldsymbol{x}_k, 0)$.
那么角度$\Theta$ 的解呢?
当位置相同时, 不应该编码任何位置信息. 令$\Theta_f:=\Theta_q=\Theta_k$, 根据$\Theta_q\left(\boldsymbol{x}_q, m\right)-\theta_q=\Theta_k\left(\boldsymbol{x}_k, m\right)-\theta_k$, 此时明显两侧是相同的函数. 由此, 可以推断出$\Theta_f\left(\boldsymbol{x}_{\{q, k\}}, m\right)-\theta_{\{q, k\}}$ 是与位置$m$ 相关, 与Word Embedding $\boldsymbol{x}_{\{q, k\}}$ 无关的函数, 可设$\Theta_f\left(\boldsymbol{x}_{\{q, k\}}, m\right)-\theta_{\{q, k\}}=\phi(m)$, 得到:
$$
\Theta_f(\boldsymbol{x}_{\{q, k\}}, m) = \phi(m) + \theta_{\{q,k\}}
$$
$n=m+1$, 将上式代入到角度关系式当中, 可以得到:
$$
\phi(m + 1) - \phi(m) = \Theta_g(\boldsymbol{x}_q, \boldsymbol{x}_k, 1) + \theta_q - \theta_k
$$
上式中右侧的常数项与绝对位置$m$ 是无关的, 所以令上式右端整体为$\theta$, $\phi(m)$ 就是一个等差数列:
$$
\phi(m) = m\theta + \gamma
$$
其中$\gamma \in \mathbb{R}$ 为常数(首项), $\theta$ 非零, 绝对位置$m$ 在这个式子中也是公差.
通过对幅值$R_f$ 和角度$\Theta_f$ 的求解, 整理一下上面的式子, 可以得到:
$$
\begin{aligned}
f_q(\boldsymbol{x}_q, m) &= \Vert \boldsymbol{q}\Vert e^{i(\theta_q + m\theta + \gamma)} = \boldsymbol{q} e^{i(m\theta + \gamma)} \\
f_k(\boldsymbol{x}_k, n) &= \Vert \boldsymbol{k}\Vert e^{i(\theta_k + n\theta + \gamma)}= \boldsymbol{k} e^{i(n\theta + \gamma)}
\end{aligned}
$$
通常$\boldsymbol{q} = f_q(\boldsymbol{x}_m, 0), \boldsymbol{k} = f_k(\boldsymbol{x}_n, 0)$ 是直接由一层投影得到的:
$$
\begin{aligned}
\boldsymbol{q} = f_q(\boldsymbol{x}_m, 0) &= \boldsymbol{W}_q\boldsymbol{x}_n\\
\boldsymbol{k} = f_k(\boldsymbol{x}_n, 0) &= \boldsymbol{W}_k\boldsymbol{x}_n
\end{aligned}
$$
方便起见, 直接设定$\gamma = 0$, 因此得到最终的RoPE形式:
$$
\begin{aligned}
f_q(\boldsymbol{x}_m, m) &= (\boldsymbol{W}_q\boldsymbol{x}_m)e^{im\theta} \\
f_k(\boldsymbol{x}_n, n) &= (\boldsymbol{W}_k\boldsymbol{x}_n)e^{in\theta}
\end{aligned}
$$
所以, 我们在二维情况下, 最后找到的函数$g$ 为:
$$
g(\boldsymbol{x}_m, \boldsymbol{x}_n, m - n) = \operatorname{Re}[(\boldsymbol{W}_q\boldsymbol{x}_m)(\boldsymbol{W}_k\boldsymbol{x}_n)^{\ast}e^{i(m - n)\theta}]
$$
其中$\text{Re}(\cdot)$ 为取复数的实部, $(\boldsymbol{W}_k\boldsymbol{x}_n)^{\ast}$ 为$(\boldsymbol{W}_k\boldsymbol{x}_n)$ 的共轭复数, $\theta \in \mathbb{R}$ 为预设好的非零常数(基波长, 沿用Transformer的原论文, 经常设为10000, 底数的选择可以参考这里).
进一步写出二维情况下$f_{q, k}$ 的表达式:
$$
\begin{aligned}
f_{\{q, k\}}(\boldsymbol{x}_m, m) &= \left(
\begin{array}{cc}
\cos{m\theta}& -\sin{m\theta} \\
\sin{m\theta}&\cos{m\theta}
\end{array}
\right)
\left(
\begin{array}{cc}
W^{(11)}_{\{q, k\}} & W^{(12)}_{\{q, k\}} \\
W^{(21)}_{\{q, k\}} & W^{(22)}_{\{q, k\}}
\end{array}
\right)
\left(
\begin{array}{cc}
x^{(1)}_m\\
x^{(2)}_m
\end{array}
\right) \\
&=\left(
\begin{array}{cc}
\cos{m\theta}& -\sin{m\theta} \\
\sin{m\theta}&\cos{m\theta}
\end{array}
\right)
\left(
\begin{array}{cc}
\{q, k\}^{(1)}_m\\
\{q, k\}^{(2)}_m
\end{array}
\right)
\end{aligned}
$$
它就是$\{\boldsymbol{q, k}\}_m$ 乘了一个旋转矩阵, 对应着空间中的向量旋转操作, 这才是RoPE(Rotary Position Embedding)名字的由来.
General form
更为普遍的, 将上节得到的二维情况扩展到任意偶数维度$d$. 将RoPE应用于$\boldsymbol{x}_i \in \mathbb{R}^d$:
$$
f_{\{q, k\}}(\boldsymbol{x}_m, m) = \boldsymbol{R}^d_{\Theta, m}\boldsymbol{W}_{\{q, k\}}\boldsymbol{x}_m
$$
非常自然的思路就是将$d$ 维拆成$d/2$ 个的二维子空间, 所以$\boldsymbol{R}^d_{\Theta, m}$ 为:
$$
\boldsymbol{R}_{\Theta, m}^d=\left(\begin{array}{ccccccc}
\cos m \theta_1 & -\sin m \theta_1 & 0 & 0 & \cdots & 0 & 0 \\
\sin m \theta_1 & \cos m \theta_1 & 0 & 0 & \cdots & 0 & 0 \\
0 & 0 & \cos m \theta_2 & -\sin m \theta_2 & \cdots & 0 & 0 \\
0 & 0 & \sin m \theta_2 & \cos m \theta_2 & \cdots & 0 & 0 \\
\vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & 0 & 0 & \cdots & \cos m \theta_{d / 2} & -\sin m \theta_{d / 2} \\
0 & 0 & 0 & 0 & \cdots & \sin m \theta_{d / 2} & \cos m \theta_{d / 2}
\end{array}\right)
$$
其中, $\Theta=\left\{\theta_i=10000^{-2(i-1) / d}, i \in[1,2, \ldots, d / 2]\right\}$. 所以$i$ 越大, $\theta_i$ 越小, 即下标越大的维度旋转速度越慢.
这篇文章提供了一个非常有意思的角度, 不同角速度的维度就像时针分针秒针一样, 通过不同的快慢角速度来组合表征一个位置信息.
将RoPE直接作用于Self-Attention, 可得:
$$
\boldsymbol{q}_m^{\intercal}\boldsymbol{k}_n
=(\boldsymbol{R}^d_{\Theta, m}\boldsymbol{W}_q\boldsymbol{x}_m)^\intercal(\boldsymbol{R}^d_{\Theta, n}\boldsymbol{W}_k\boldsymbol{x}_n) =\boldsymbol{x}^\intercal\boldsymbol{W}_qR^d_{\Theta, n-m}\boldsymbol{W}_k\boldsymbol{x}_n
$$
其中, $\boldsymbol{R}_{\Theta, n-m}^d=\left(\boldsymbol{R}_{\Theta, m}^d\right)^{\top} \boldsymbol{R}_{\Theta, n}^d$. 由于$\boldsymbol{R}_{\Theta}^d$ 是一个正交矩阵, 所以它在编码位置信息的时候是相对稳定的.
RoPE相较于之前位置编码的最大不同, 在于它是乘性的, 而不是加性的, 因此它在编码的相对位置信息可以天然的融入到Self-Attention的内积中.
Properties of RoPE
RoPE有一些优良的性质.
首先, RoPE具有长程衰减, 和最早版本的Transformer一样, RoPE设定$\theta_i=10000^{-2i/d}$, 底数$\theta$ 越大长程衰减越慢.
其次, RoPE在Linear Attention当中可以使得Self-Attention被更一般的形式重写.
例如, 常规的SDPA可以写成:
$$
\operatorname{Attention}(\mathbf{Q},\mathbf{K},\mathbf{V})_m=\frac{\sum_{n=1}^{N}\operatorname{sim}(\boldsymbol{q}_m,\boldsymbol{k}_n)\boldsymbol{v}_n}{\sum_{n=1}^{N}\operatorname{sim}(\boldsymbol{q}_m, \boldsymbol{k}_n)}
$$
Self-Attention中采用的是$\operatorname{sim}\left(\boldsymbol{q}_m, \boldsymbol{k}_n\right)=\exp \left(\boldsymbol{q}_m^{\top} \boldsymbol{k}_n / \sqrt{d}\right)$, 它具有$\mathbb{O}(N^2)$ 的复杂度.
Linear Attention的复杂度是比SDPA更低的线性复杂度, 形式如下:
$$
\operatorname{Attention}(\mathbf{Q},\mathbf{K},\mathbf{V})_m=\frac{\sum_{n=1}^{N}\phi(\boldsymbol{q}_m)^{\intercal}\varphi(\boldsymbol{k}_n)\boldsymbol{v}_n}{\sum_{n=1}^{N}\phi(\boldsymbol{q}_m)^{\intercal}\varphi(\boldsymbol{k}_n)}
$$
其中$\phi(\cdot), \varphi(\cdot)$ 通常是非负函数, 例如$\phi(x)=\varphi(x)=\text{elu}(x)+1$, 或者$\phi\left(\boldsymbol{q}_i\right)=\operatorname{softmax}\left(\boldsymbol{q}_i\right), \varphi\left(\boldsymbol{k}_j\right)=\exp \left(\boldsymbol{k}_j\right)$.
由于RoPE的存在, 可以使得Hidden State的范数不变, 因此可以将RoPE直接乘, 从而无缝集成到Linear Attention中, 从而不增加Linear Attention的复杂度:
$$
\operatorname{Attention}(\mathbf{Q},\mathbf{K},\mathbf{V})_m=\frac{\sum_{n=1}^{N}\big(\boldsymbol{R}^d_{\Theta, m}\phi(\boldsymbol{q}_m)\big)^{\intercal}\big(\boldsymbol{R}^d_{\Theta, n}\varphi(\boldsymbol{k}_n)\big)\boldsymbol{v}_n}{\sum_{n=1}^{N}\phi(\boldsymbol{q}_m)^{\intercal}\varphi(\boldsymbol{k}_n)}
$$
Theoretical Explanation
Computational efficient realization of rotary matrix multiplication
由于$\boldsymbol{R}^d_{\Theta, m}$ 是一个稀疏矩阵, 所以它的计算效率很低. 下式可以化简计算:
$$
\boldsymbol{R}^d_{\Theta, m}\boldsymbol{x} =
\begin{pmatrix}
x_1\\
x_2\\
x_3\\
x_4\\
\vdots\\
x_{d-1}\\
x_d
\end{pmatrix}
\otimes
\begin{pmatrix}
\cos{m\theta_1} \\
\cos{m\theta_1} \\
\cos{m\theta_2} \\
\cos{m\theta_2} \\
\vdots \\
\cos{m\theta_{d/2}} \\
\cos{m\theta_{d/2}}
\end{pmatrix}
+
\begin{pmatrix}
-x_2\\
x_1\\
-x_4\\
x_3\\
\vdots\\
-x_d\\
x_{d-1}
\end{pmatrix}
\otimes
\begin{pmatrix}
\sin{m\theta_1}\\
\sin{m\theta_1}\\
\sin{m\theta_2}\\
\sin{m\theta_2}\\
\vdots\\
\sin{m\theta_{d/2}}\\
\sin{m\theta_{d/2}}
\end{pmatrix}
$$
其中$\otimes$ 为逐元素点乘.
Long-term decay of RoPE
在RoPE的作用下, 将向量$\boldsymbol{q}=\boldsymbol{W}_q\boldsymbol{x}_m, \boldsymbol{k}=\boldsymbol{W}_k\boldsymbol{x}_n$ 两维两维的分组成对, 其内积可以写成:
$$
(\boldsymbol{R}^d_{\Theta, m}\boldsymbol{W}_q\boldsymbol{x}_m)^\intercal(\boldsymbol{R}^d_{\Theta, n}\boldsymbol{W}_k\boldsymbol{x}_n) = \operatorname{Re}\bigg[\sum_{i=0}^{d/2-1}\boldsymbol{q}_{[2i:2i+1]}\boldsymbol{k}_{[2i:2i+1]}^{\ast}e^{i(m-n)\theta_{i}}\bigg]
$$
其中$\boldsymbol{q}_{[2i:2i+1]}$ 代表$\boldsymbol{q}$ 中的第$2i$ 到第$2i+1$ 个元素, $\boldsymbol{k}$ 同理.
令$h_i = \boldsymbol{q}_{[2i:2i+1]}\boldsymbol{k}_{[2i:2i+1]}^\ast, S_j = \sum_{i=0}^{j-1} e^{\text{i}(m-n)\theta_i}$, 同时设$h_{d/2}=0, S_0=0$, 由Abel变换可以得到:
$$
\sum_{i=0}^{d/2-1}\boldsymbol{q}_{[2i:2i+1]}\boldsymbol{k}_{[2i:2i+1]}^{\ast}e^{i(m-n)\theta_{i}}=\sum_{i=0}^{d/2-1}h_i(S_{i+1}-S_{i})=-\sum_{i=0}^{d/2-1}S_{i+1}(h_{i+1}-h_i)
$$
因此有:
$$
\begin{aligned}
\bigg\vert\sum_{i=0}^{d/2-1}\boldsymbol{q}_{[2i:2i+1]}\boldsymbol{k}_{[2i:2i+1]}^{\ast}e^{i(m-n)\theta_{i}}\bigg\vert &= \bigg\vert\sum_{i=0}^{d/2-1}S_{i+1}(h_{i+1}-h_i)\bigg\vert\\
&\leq \sum_{i=0}^{d/2-1}\vert S_{i+1}\vert\vert(h_{i+1}-{h_i})\vert\\
&\leq \big(\max_i\vert h_{i+1}-h_i\vert\big)\sum_{i=0}^{d/2-1}\vert S_{i+1}\vert
\end{aligned}
$$
即当相对位置$m-n$ 增大时, 在$\theta_i=10000^{-2i/d}$的设定下, $\frac{1}{d / 2} \sum_{i=1}^{d / 2}\left|S_i\right|$ 的值是逐渐减小的, 如下图所示:
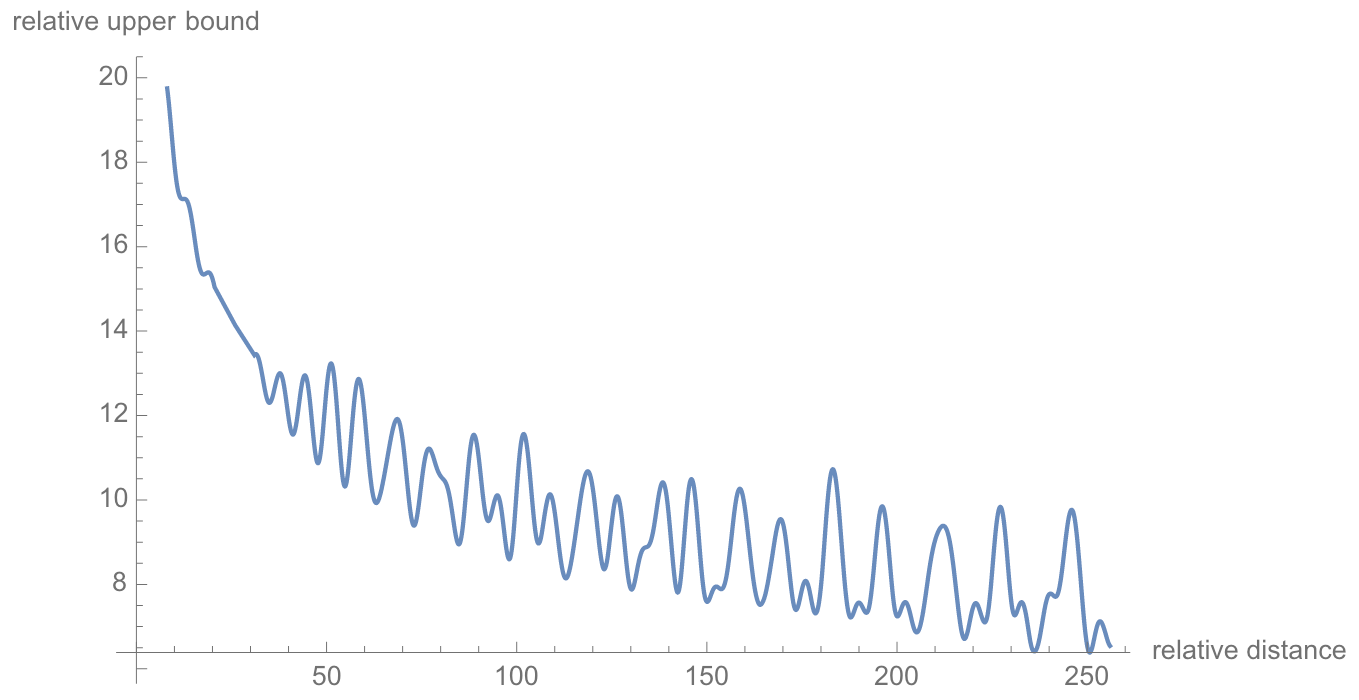
Experiments and Evaluations
详细的实验参数设置和模型参数设置请参考原论文.
Machine Translation
作者将RoFormer与Vallina Transformer在WMT 2014 English-German(450w平行语料)上对比:

RoFormer略高于Vallina Transformer.
Pre-training Language Modeling
接着, 在BookCorpus和Wikipedia这两个常用的语料上做预训练, 与BERT做对比, 结果如下:
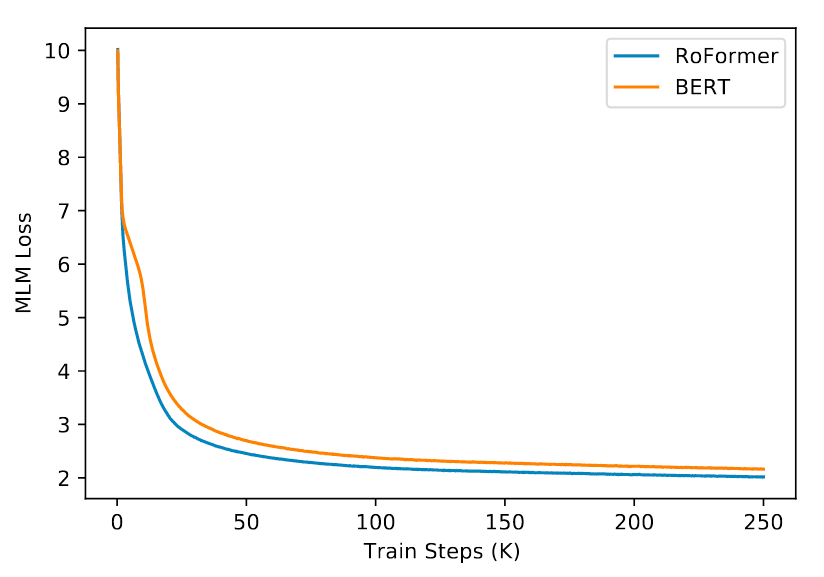
RoFormer明显的比BERT要收敛更快一些, 而且从曲线上来看它的训练看起来更加稳定.
Fine-tuning on GLUE tasks
在GLUE上做Finetune, 继续与BERT对比:

RoFormer在MRPC, STS-B, QQP上有显著优势, 它们都是偏语义类的任务, 在SST-2和QNLI, MNLI中表现弱于BERT.
Performer with RoPE
上文中提到了RoPE在Linear Attention中的优势, 因此测试与使用Linear Attention的Performer做个结合:
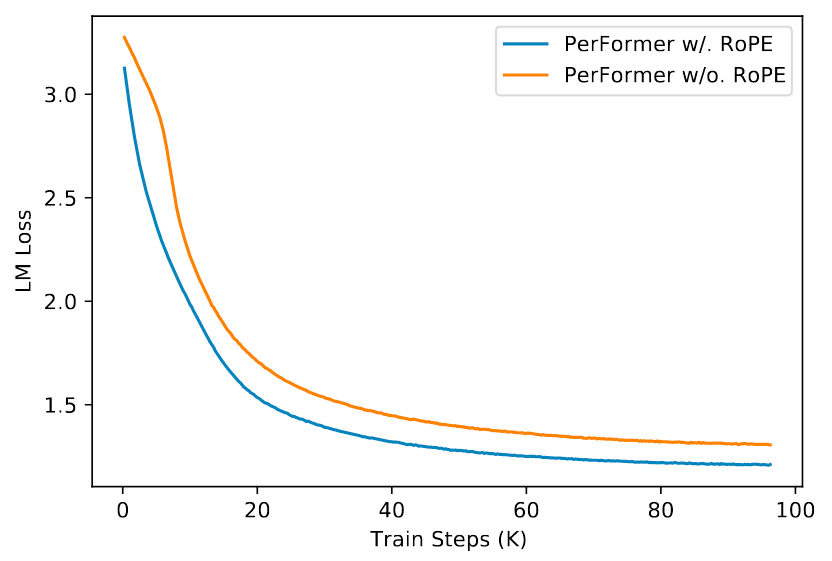
RoPE能够在维持原复杂度不变的条件下加速收敛.
Evaluation on Chinese Data
除了在英文数据上进行评估, 还要在中文数据上进行评估.
在本实验中, 作者将自己提出的WoBERT的绝对位置编码替换为RoPE:

并在34G的语料上进行不同参数的多阶段训练, 以适应不同的输入长度:
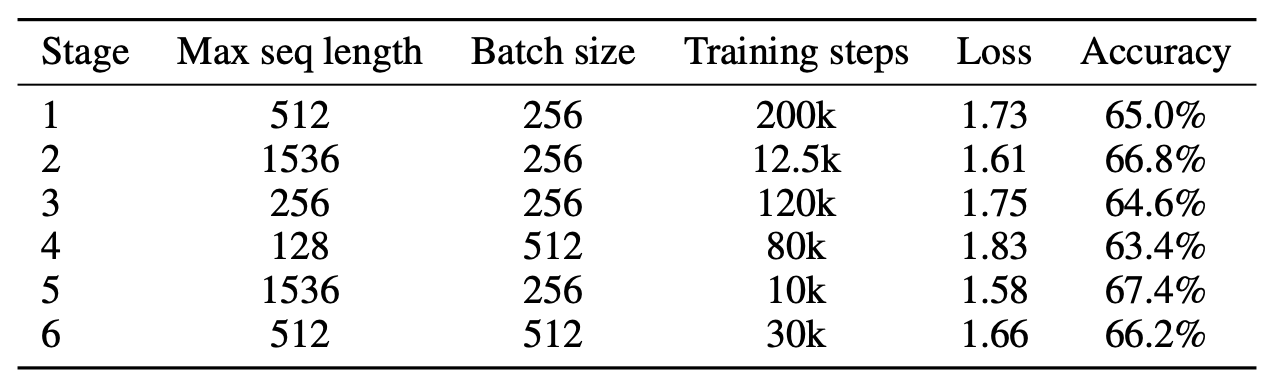
随着序列长度的增加, RoFormer总是能取得更好的性能, 说明RoFormer在长度外推设置下表现较好.
在CAIL2019-SCM(一个语义相似任务)上来测试RoFormer的长文本能力, 表现如下:
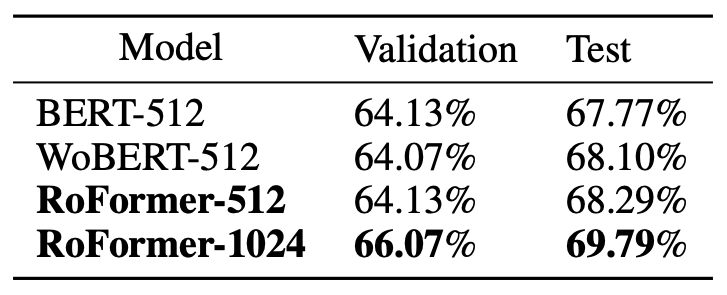
- 当RoFormer输入长为512时, 能够略优于BERT和WoBERT.
- 当RoFormer的最大输入长度扩展到1024的时候, 显著优于BERT和WoBERT.
此外, 还能观察到在中文场景下, 词建模的WoBERT要优于字建模的BERT. 我以前也有类似的观点, 更大的优势是词建模如果用到生成类任务中能带来更快的推理速度.
Summary
与其说RoPE简洁旦优雅, 不如说RoPE简洁甚至优雅. RoPE用绝对位置编码实现了相对位置编码, 并且能够丝滑无缝的融入到Self-Attention当中.
由于我硕士期间是做信息抽取的, 所以我印象中RoPE最早在信息抽取里面运用的非常广泛, 其中可能原因有两个:
- 其一是因为相对位置对信息抽取的Span抽取影响比较大, 因为每个Span的都是通过起止边界位置确定的, 在Universal Information发展后期, 基本都是要带上RoPE.
- 另外可能是因为信息抽取抽取Span的大多都是通过一个乘积计算得到得分, 与内积形式一致, 这与RoPE给Self-Attention设计的形式恰恰好是一致的, 所以RoPE表现好也不奇怪.
RoPE早期在其他领域似乎没有得到特别多的关注. 但是随着PaLM, LLaMA等LLM采用了RoPE, RoPE便渐渐的在LLM里面成为一项标准的配置, 所以RoPE甚至也被人誉为LLM时代的ResNet.
在更长的上下文场景下, RoPE的续作是ReRoPE, 超过了NTK-RoPE, 感兴趣的可以继续深入.
虽然论文本身不是苏神自己写的, 但最后在文末也不得不感叹, 苏神真强啊.

