本文前置知识:
Flow Matching for Generative Modeling
- 论文: Flow Matching for Generative Modeling, Meta AI, ICLR 2023.
- 代码: GitHub - facebookresearch/flow_matching: A PyTorch library for implementing flow matching algorithms, featuring continuous and discrete flow matching implementations. It includes practical examples for both text and image modalities.
同期工作与Flow Matching撞车, 本文中的Flow Matching实际上推导出了一种Diffusion Model的更通用的形式, 它们都是在建立已知的噪声分布到数据分布之间的变换关系.
- 如果对Rectified Flow还不够了解, 还是推荐先看Rectified Flow.
- 如果比较关心的是Flow-based Model在应用 / 实现方面的内容, 其实可以不用看本文, 不然会很痛苦.
Continuous Normalizing Flow
对于某空间中数据分布中的数据点$x=(x^1, \dots, x^d) \in \mathbb{R}^d$, 在这个空间中有如下定义:
- 概率密度路径$p:[0,1] \times \mathbb{R}^d \rightarrow \mathbb{R}_{>0}$ 是一个满足$\int{p_t(x) dx=1}$ 且与时间$t$ 相关的概率密度函数.
- 与时间$t$ 相关的向量场$v:[0,1] \times \mathbb{R}^d \rightarrow \mathbb{R}^d$.
由于二者都是与时间$t$ 相关的, 出于习惯将$t$ 写在下角标.
向量场$v_t$ 中可以构造一个与时间相关的微分同胚映射, 即流(Flow) $\phi: [0, 1] \times \mathbb{R}^d \rightarrow \mathbb{R}^d$, 它可以用常微分方程(ODE)来定义:
$$
\begin{aligned}
\frac{d}{d t} \phi_t(x) & =v_t\left(\phi_t(x)\right) \\
\phi_0(x) & =x
\end{aligned}
$$
因此:
- 流$\phi_t(x)$ 可以理解为获取$t$ 时刻$x$ 在向量场$v_t$ 内的位置的映射, 把它可以想象成一只有目的地的小船.
- 向量场$v_t$ 可以表征流$\phi_t(x)$ 在$t$ 时刻变化的大小与方向, 可以把它想象成承载小船的河流中的水流.
向量场$v_t$ 其实可以用神经网络来拟合, 记为$v_t(x;\theta)$, 其中$\theta$ 为可学习参数. 在这种视角下的$\phi_t$ 也可以看做是一个深度参数化的模型, 可以称之为Continuous Normalizing Flow(CNF).
注: 它们之间关系的本质是流$\phi_t(x)$ 是通过向量场$v_t$ 实现的.
CNF可以将一个相对简单的先验概率密度$p_0$ 转换为(推送到, Push-Forward)一个更复杂的概率密度$p_1$:
$$
p_t=\left[\phi_t\right]_\ast p_0
$$
其中的Push-Forward操作符$\ast$ 含义为:
$$
\left[\phi_t\right]_\ast p_0(x)=p_0\left(\phi_t^{-1}(x)\right) \operatorname{det}\left[\frac{\partial \phi_t^{-1}}{\partial x}(x)\right]
$$
如果一个向量场$v_t$ 的流$\phi_t$ 满足$p_t=\left[\phi_t\right]_\ast p_0$, 则称$v_t$ 在$\phi_t$ 下生成了一条概率密度路径$p_t$.
综上, CNF的目的就是用数据驱动来训练向量场(耗时耗力开凿河道以引导流向和水速), 进而实现初始概率分布$p_0$ 到目的概率分布$p_1$ 的转换(推动小船到达目的地).
训练完成后的向量场$v_t$ 在不同的时间下应该长这个样子:
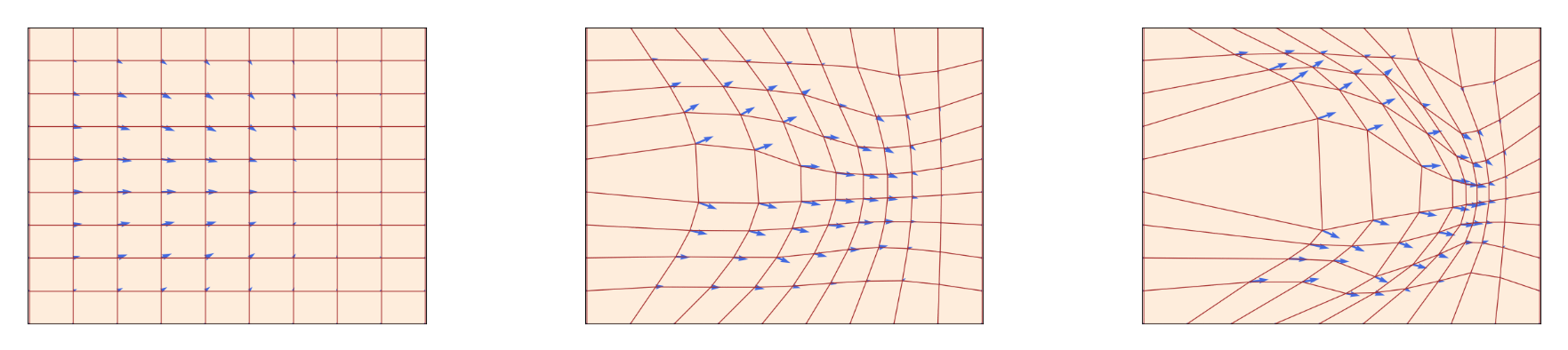
通过向量场, 将分布$p_0$ 转换为$p_1$:
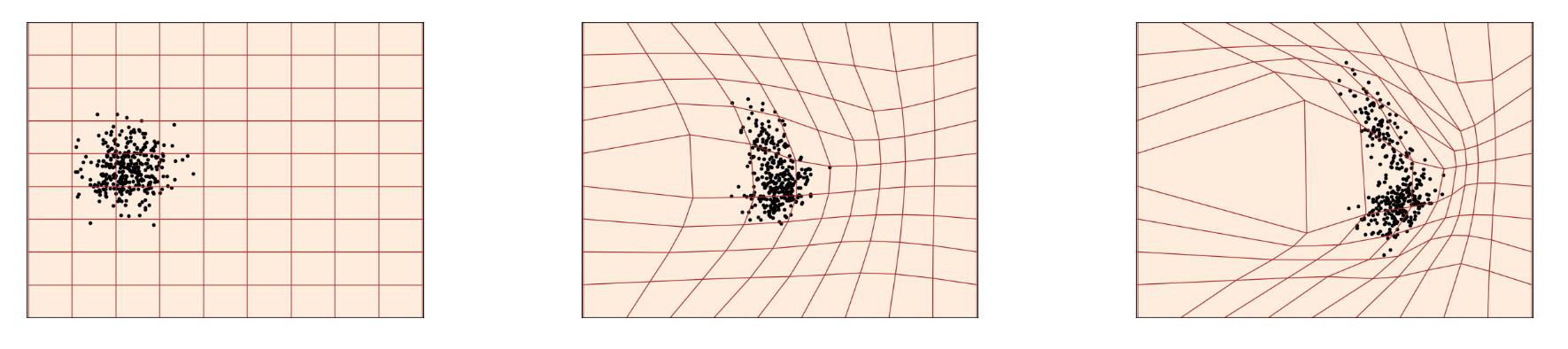
可以用连续性方程(Continuity Equation)来验证场生成概率密度路径的合理性, 即:
$$
\frac{d}{d t} p_t(x)+\operatorname{div}\left(p_t(x) v_t(x)\right)=0
$$
即对于任意时刻$t$, 在场$v_t$ 中概率密度$p_t$ 的变化量$\frac{d}{d t} p_t(x)$ 一定和概率流的净流出量$-\operatorname{div}\left(p_t(x) v_t(x)\right)$ 相等. 在后面的推导中, 它是一个至关重要的约束条件.
Flow Matching
有了CNF的定义, 下面进入正题.
假如有一随机变量$x_1$ 来自于未知的数据分布$q(x_1)$. 我们没法直接访问$q(x_1)$ 的概率密度函数本身, 但是可以访问这个分布中的一些样本.
我们可以构造一个概率路径$p_t$, 其起点$p_0=p$ 为一个已知的简单分布, 比如标准正态分布$p(x)=\mathcal{N}(x \mid 0, I)$, 终点$p_1$ 近似于$q$. Flow Matching可以帮助我们找到这个由$p_0$ 到$p_1$ 的概率路径, 从而建模已知分布$p_0$ 转移到数据分布$p_1$ 的过程:
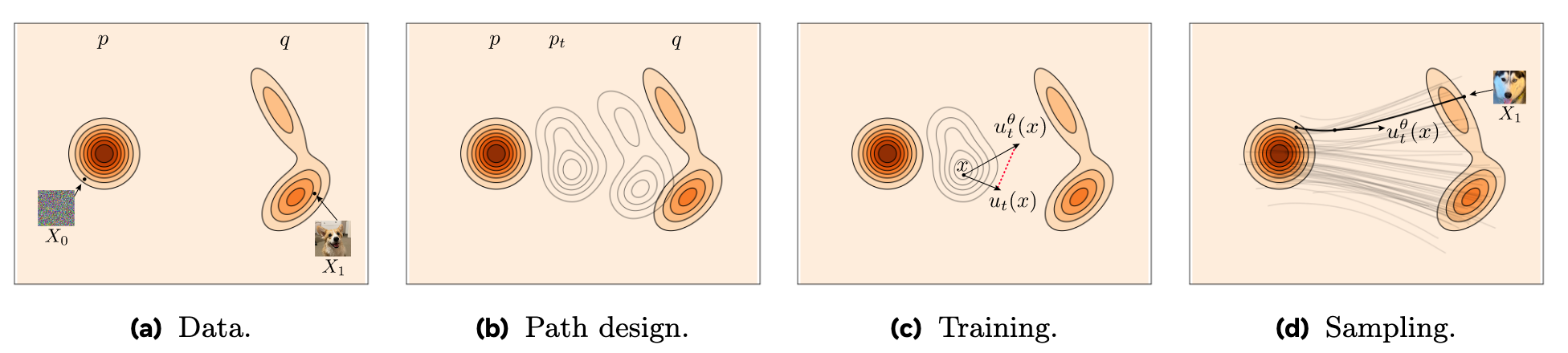
对于要学的目标概率密度路径$p_t(x)$ 和其对应的目标向量场$u_t(x)$, Flow Matching的训练目标为:
$$
\mathcal{L}_{\mathrm{FM}}(\theta)=\mathbb{E}_{t, p_t(x)}\left\Vert v_t(x)-u_t(x)\right\Vert ^2
$$
其中, $\theta$ 为参数化向量场$v_t$ 的可学习参数, $t \sim \mathcal{U}[0, 1]$, $x \sim p_t(x)$. 当Loss接近0的时候, 就可以将$v_t(x;\theta)$ 近似为$u_t(x)$, 以此可以用来生成概率密度路径$p_t(x)$.
然而, 我们对$p_t$ 和$u_t$ 完全未知, 而且会有很多概率路径都能够满足$p_1(x)\approx q(x)$.
Constructing Target from Conditional Probability Paths and Vector Fields
由于没法直接访问$q(x_1)$, 但是可以访问它的样本点. 所以可以考虑将$p_t$ 拆分为多个子问题, 即求解$p_t$ 在各样本点下的条件概率路径的混合.
对于一个给定的样本$x_1$, 将$p_t(x \mid x_1)$ 表示一个条件概率路径, 使$t=0$ 时满足$p_0(x \mid x_1)=p(x)$, 且令$t=1$ 时满足$p_1(x \mid x_1)$ 为集中在$x_1$ 附近的分布, 例如$\mathcal{N}(x \mid x_1, \sigma^2 I)$, 只要满足$x_1$ 为均值和足够小的标准差$\sigma > 0$ 就可以.
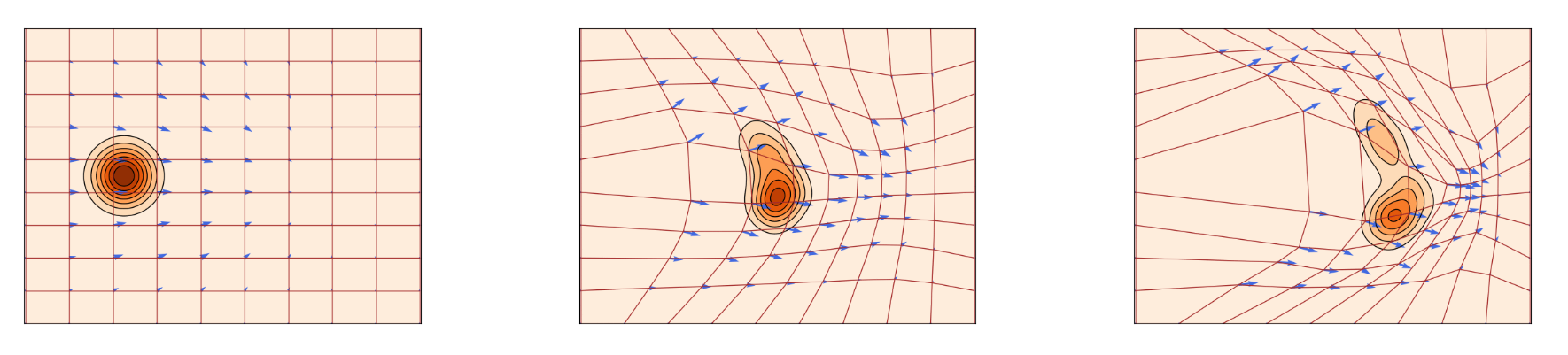
这个概念其实推荐在看完下面的边缘化后, 结合本小节最后的那副图强化一下印象.
因此, 通过对$q(x_1)$ 的边缘化, 得到$t$ 时刻的边缘概率路径$p_t(x)$:
$$
p_t(x)=\int p_t\left(x \mid x_1\right) q\left(x_1\right) d x_1
$$
时间$t=1$ 时, 边缘概率$p_1$ 需要能够近似$q$:
$$
p_1(x)=\int p_1\left(x \mid x_1\right) q\left(x_1\right) d x_1 \approx q(x)
$$
回过头来, 为什么说条件向量场能够表示边缘向量场呢, 这里面有什么根据吗? 根据连续性方程, 可以证明:
$$
\begin{aligned}
\frac{d}{d t} p_t(x) & =\int\left(\frac{d}{d t} p_t\left(x \mid x_1\right)\right) q\left(x_1\right) d x_1=-\int \operatorname{div}\left(u_t\left(x \mid x_1\right) p_t\left(x \mid x_1\right)\right) q\left(x_1\right) d x_1 \\
& =-\operatorname{div}\left(\int u_t\left(x \mid x_1\right) p_t\left(x \mid x_1\right) q\left(x_1\right) d x_1\right)=-\operatorname{div}\left(u_t(x) p_t(x)\right)
\end{aligned}
$$
将边缘概率路径转换为条件概率路径后, 是否也存在对应的边缘向量场转化为条件向量场呢? 其实答案就隐藏在刚才的推导里. 在最后两个等号中, 除去散度符号$\operatorname{div}$, 不难发现有:
$$
u_t(x) p_t(x) = \int u_t\left(x \mid x_1\right) p_t\left(x \mid x_1\right) q\left(x_1\right) d x_1
$$
因此, 便可以给出条件向量场表示的边缘向量场定义(假设$p_t(x)>0$):
$$
u_t(x)=\int u_t\left(x \mid x_1\right) \frac{p_t\left(x \mid x_1\right) q\left(x_1\right)}{p_t(x)} d x_1
$$
其中$u_t(\cdot \mid x_1): \mathbb{R}^d \rightarrow \mathbb{R}^d$ 为生成条件概率路径$p_t(\cdot | x_1)$ 的条件向量场.
因此, 便能够得出一个非常重要的结论: 如果给定的能够生成条件概率路径$p_t(x \mid x_1)$ 的条件向量场$u_t(x \mid x_1)$, 对于任意分布$q(x_1)$, 边缘向量场$u_t$ 都能生成边缘概率路径$p_t$, 且$p_t$, $u_t$ 满足连续性方程.
如果上面看的迷迷糊糊的, 下面这幅图非常清晰的说明了条件概率路径$p_t(x \mid x_1)$, 边缘概率路径$p_t(x)$, 条件速度场$u_t(x \mid x_1)$ 和边缘速度场$u_t(x)$ 的区别:
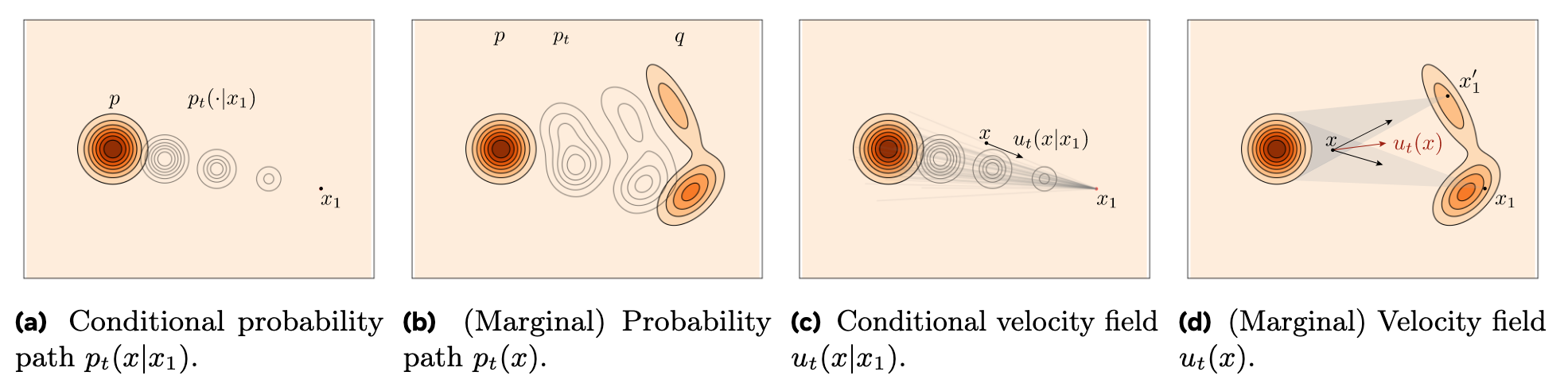
Conditional Flow Matching
即便用条件概率路径$p_t\left(x \mid x_1\right)$, 条件向量场来$u_t\left(x \mid x_1\right)$表示了边缘概率路径$p_t(x)$, 边缘向量场$u_t(x)$, 但是因为它们有积分, 而我们只能访问到实际分布的部分样本, 所以还是难以求解. 对于原来的Flow Matching Objective $\mathcal{L}_{\text {FM}}$ 中, 求解是不太可能的.
直觉上来说, 如果直接学条件向量场有没有可能呢? 对于Conditional Flow Matching, 要学习的是一个条件向量场$u_t\left(x \mid x_1\right)$, 其训练目标为:
$$
\mathcal{L}_{\mathrm{CFM}}(\theta)=\mathbb{E}_{t, q\left(x_1\right), p_t\left(x \mid x_1\right)}\left\Vert v_t(x)-u_t\left(x \mid x_1\right)\right\Vert ^2
$$
其中$t \sim \mathcal{U}[0,1]$, $x_1 \sim q(x_1)$, $x \sim p_t(x \mid x_1)$. 此时的$p_t(x \mid x_1)$, $u_t(x \mid x_1)$ 只依赖于单个样本, 所以可以从$q(x_1)$ 中随便采样$x_1$ 来计算$p_t(x \mid x_1)$, $u_t(x \mid x_1)$.
所以这个Loss其实和Rectified Flow的训练目标是一样的.
这俩目标函数有什么区别? 观察一下:
$$
\begin{equation}
\begin{aligned}
\mathcal{L}_{\text{FM}}=\left\Vert v_t(x)-u_t(x)\right\Vert ^2 & =\left\Vert v_t(x)\right\Vert ^2-2\left\langle v_t(x), u_t(x)\right\rangle+\left\Vert u_t(x)\right\Vert ^2 \\
\mathcal{L}_{\text{CFM}}=\left\Vert v_t(x)-u_t\left(x \mid x_1\right)\right\Vert ^2 & =\left\Vert v_t(x)\right\Vert ^2-2\left\langle v_t(x), u_t\left(x \mid x_1\right)\right\rangle+\left\Vert u_t\left(x \mid x_1\right)\right\Vert ^2
\end{aligned}
\end{equation}
$$
最后一项$\left\Vert u_t(x)\right\Vert ^2$, $\left\Vert u_t\left(x \mid x_1\right)\right\Vert ^2$ 是Ground Truth, 所以它与参数$\theta$ 的优化显然无关.
两个式子中的第一项$\left\Vert v_t(x)\right\Vert ^2$ 外面挂的期望不一样, 事实证明它们是相等的:
$$
\begin{equation}
\begin{aligned}
\mathbb{E}_{p_t(x)}\left\Vert v_t(x)\right\Vert ^2 & =\int\left\Vert v_t(x)\right\Vert ^2 p_t(x) d x=\int\left\Vert v_t(x)\right\Vert ^2 p_t\left(x \mid x_1\right) q\left(x_1\right) d x_1 d x \\
& =\mathbb{E}_{q\left(x_1\right), p_t\left(x \mid x_1\right)}\left\Vert v_t(x)\right\Vert ^2
\end{aligned}
\end{equation}
$$
第二项也是相等的:
$$
\begin{equation}
\begin{aligned}
\mathbb{E}_{p_t(x)}\left\langle v_t(x), u_t(x)\right\rangle & =\int\left\langle v_t(x), \frac{\int u_t\left(x \mid x_1\right) p_t\left(x \mid x_1\right) q\left(x_1\right) d x_1}{p_t(x)}\right\rangle p_t(x) d x \\
& =\int\left\langle v_t(x), \int u_t\left(x \mid x_1\right) p_t\left(x \mid x_1\right) q\left(x_1\right) d x_1\right\rangle d x \\
& =\int\left\langle v_t(x), u_t\left(x \mid x_1\right)\right\rangle p_t\left(x \mid x_1\right) q\left(x_1\right) d x_1 d x \\
& =\mathbb{E}_{q\left(x_1\right), p_t\left(x \mid x_1\right)}\left\langle v_t(x), u_t\left(x \mid x_1\right)\right\rangle,
\end{aligned}
\end{equation}
$$
所以经过上面一通折腾, 得到一个结论:
假设$p_t(x) > 0$, 在独立于参数$\theta$ 的常数意义下, 有$\mathcal{L}_{\text {FM}}$ 与$\mathcal{L}_{\text {CFM}}$ 等价, 且$\nabla_\theta \mathcal{L}_{\text{FM}}(\theta)=\nabla_\theta \mathcal{L}_{\text {CFM}}(\theta)$.
因此, 可以通过直接学习Conditional Flow Matching来获得一个等价于Flow Matching得到的向量场, Conditional Flow Matching可以作为Flow Matching的代理目标.
Conditional Probability Paths and Vector Fields
现在已知通过Conditional Flow Matching能完成Flow Matching的训练, 接下来该着手$p_t(x \mid x_1)$ 与$u_t(x \mid x_1)$ 的构造了.
一般的, 可以考虑高斯条件概率路径$p_t\left(x \mid x_1\right)$:
$$
p_t\left(x \mid x_1\right)=\mathcal{N}\left(x \mid \mu_t\left(x_1\right), \sigma_t\left(x_1\right)^2 I\right)
$$
其中$\mu : [0, 1] \times \mathbb{R}^d \rightarrow \mathbb{R}^d$ 为与时间相关的高斯分布均值, $\sigma :[0, 1] \times \mathbb{R}^d \rightarrow \mathbb{R}_{>0}$ 为与时间相关的标准差.
简单的令$\mu_0(x_1)=0, \sigma_0(x_1)=1$, $t=0$ 时就有$p(x)=\mathcal{N}(x \mid 0, I)$. 继续令$\mu_1(x_1)=x_1, \sigma_1(x_1)=\sigma_{\min}$, $t=1$ 时$p_1(x \mid x_1)$ 为集中在$x_1$ 附近的高斯分布.
有无数中方法都能生成满足条件的概率路径, 我们可以简单点, 直接将Flow建模为高斯分布:
$$
\psi_t(x)=\sigma_t\left(x_1\right) x+\mu_t\left(x_1\right)
$$
$x$ 服从标准高斯分布, $\psi_t(x)$ 为一个仿射变换, 将$x$ 映射为均值$\mu_t(x_1)$, 标准差$\sigma_t(x_1)$ 的正态分布变量.
这个形式就和Diffusion Model的建模形式一样了, 为噪声$x$ 和目标样本$x_1$ 之间的线性组合.
而流$\psi_t(x)$ 可以将噪声分布$p_0(x \mid x_1)=p(x)$ 推到$p_t(x \mid x_1)$:
$$
\left[\psi_t\right]_\ast p(x)=p_t\left(x \mid x_1\right)
$$
流$\psi_t$ 提供了如下生成条件概率路径的条件向量场$u_t$:
$$
\frac{d}{d t} \psi_t(x)=u_t\left(\psi_t(x) \mid x_1\right)
$$
对$p_t(x \mid x_1)$ 做仅关于$x_0$ 的重参数, 代入到CFM的目标$\mathcal{L}_{\text{CFM}}$ 中有:
$$
\mathcal{L}_{\text {CFM }}(\theta)=\mathbb{E}_{t, q\left(x_1\right), p\left(x_0\right)}\left\Vert v_t\left(\psi_t\left(x_0\right)\right)-\frac{d}{d t} \psi_t\left(x_0\right)\right\Vert ^2
$$
$\psi_t$ 为简单的可逆仿射映射, 且它的唯一向量场具有如下形式:
$$
u_t\left(x \mid x_1\right)=\frac{\sigma_t^{\prime}\left(x_1\right)}{\sigma_t\left(x_1\right)}\left(x-\mu_t\left(x_1\right)\right)+\mu_t^{\prime}\left(x_1\right)
$$
$u_t\left(x \mid x_1\right)$ 就可以生成高斯路径$p_t\left(x \mid x_1\right)$. 至此, 我们就完成了条件向量场$u_t\left(x \mid x_1\right)$ 形式的构造.
不过$u_t\left(x \mid x_1\right)$ 是怎么推导得到的?
令条件向量场$u_t(x \mid x_1)=w_t(x)$, 结合Flow $\psi_t$ 有:
$$
\frac{d}{d t} \psi_t(x)= w_t\left(\psi_t(x)\right)
$$
由于$\psi_t$ 可逆, 令$x=\psi_t^{-1}(y)$, 有:
$$
\psi_t^\prime(\psi^{-1}_{t}(y))=w_t(y)
$$
需要计算$\psi_t$ 对时间的导数. 别忘了前面定义过, $\psi_t$ 为一个高斯路径流, $x$ 为与时间无关的常数, 所以其对时间$t$ 的导数为:
$$
\psi_t^\prime(x) = \sigma^\prime_t(x_1) x + \mu_t^\prime(x_1)
$$
根据$\psi_t(x)$, 写出$x$ 的表达式:
$$
x = \frac{\psi_t(x) - \mu_t(x_1)}{\sigma_t(x_1)} = \frac{y - \mu_t(x_1)}{\sigma_t(x_1)}
$$
将$x$ 代入$\psi_t^\prime(x)$ 当中可得:
$$
\psi_t^\prime(x) = \frac{\sigma_t^{\prime}\left(x_1\right)}{\sigma_t\left(x_1\right)}\left(y-\mu_t\left(x_1\right)\right)+\mu_t^{\prime}\left(x_1\right)
$$
$\psi_t^\prime(\psi^{-1}_{t}(y))= \psi_t^\prime(x)=w_t(y)$, 有:
$$
w_t\left(y\right)=\frac{\sigma_t^{\prime}\left(x_1\right)}{\sigma_t\left(x_1\right)}\left(y-\mu_t\left(x_1\right)\right)+\mu_t^{\prime}\left(x_1\right)
$$
得证. 且该式子对于任意的$\mu_t(x_1), \sigma_t(x_1)$ 都是可用的.
Special Instances of Gaussian Conditional Probability Paths
Diffusion Conditional VFs
Diffusion Model的Forward Process本身就是将目标样本$x_1$ 不断加噪, 然后得到纯噪声$x_0$ 的过程, 所以它可以被看做是一个随机过程.
对于Diffusion Model来说, 有两种Reverse Process可选.
一种是Variance Exploding(VE)方差爆炸型, 其概率路径$p_t\left(x \mid x_1\right)$ 形式为:
$$
p_t\left(x \mid x_1\right)=\mathcal{N}\left(x \mid x_1, \sigma_{1-t}^2 I\right)
$$
其中$\sigma_t$ 为递增函数, $\sigma_0 =0, \sigma_1 \gg 1$, 所以$t=1$ 时, $\sigma_0=0$, 集中在目标数据分布旁, $t=0$ $\sigma_1 \gg 1$, 接近纯噪声. 但是由于没有对$x_1$ 前面加调整的系数, 所以会导致整体的方差非常大.
在上式中, $p_t\left(x \mid x_1\right)$ 的$\mu_t(x_1) = x_1$, $\sigma_t(x_1) = \sigma_{1-t}$, 代入$u_t\left(x \mid x_1\right)$ 中可得:
$$
u_t\left(x \mid x_1\right)=-\frac{\sigma_{1-t}^{\prime}}{\sigma_{1-t}}\left(x-x_1\right)
$$
另一种为Variance Preserving(VP)方差保持型, 其概率路径$p_t\left(x \mid x_1\right)$ 形式为:
$$
p_t\left(x \mid x_1\right)=\mathcal{N}\left(x \mid \alpha_{1-t} x_1,\left(1-\alpha_{1-t}^2\right) I\right), \text { where } \alpha_t=e^{-\frac{1}{2} T(t)}, T(t)=\int_0^t \beta(s) d s
$$
其中, $\beta$ 为噪声缩放函数. 当$t=1$ 时, $a_0=1$ 接近目标数据分布, $t=0$ 时, $a_1 \approx 0$, 接近于纯噪声.
$p_t\left(x \mid x_1\right)$ 的$\mu_t(x_1) = \alpha_{1-t}x_1, \sigma_t(x_1) = \sqrt{1-\alpha_{1-t}^2}$, 代入$u_t\left(x \mid x_1\right)$ 中可得:
$$
u_t\left(x \mid x_1\right)=\frac{\alpha_{1-t}^{\prime}}{1-\alpha_{1-t}^2}\left(\alpha_{1-t} x-x_1\right)=-\frac{T^{\prime}(1-t)}{2}\left[\frac{e^{-T(1-t)} x-e^{-\frac{1}{2} T(1-t)} x_1}{1-e^{-T(1-t)}}\right]
$$
感兴趣的可以自行查阅下DDIM的附录, 上面的情况对应的向量场$u_t(x \mid x_1)$ 与DDIM里的向量场实际上是一样的. 因此, 我们沿着Flow Matching的思路就推出了经典的Diffusion Model 方法DDIM.
Optimal Transport Conditional VFs
感觉沿着Diffusion的思路构造条件向量场还是有点复杂了些. 在条件概率路径中, 一个更直接更简单方法是直接让均值$\mu_t(x)$ 和标准差$\sigma_t(x)$ 都随时间线性变化, 即希望这条路径为一条空间中的直线:
$$
\begin{gathered}
\mu_t(x)=tx_1 \\
\sigma_t(x)=1-(1-\sigma_{\text{min}})t
\end{gathered}
$$
在这种设定下, 代入$u_t\left(x \mid x_1\right)$ 中可得:
$$
u_t\left(x \mid x_1\right)=\frac{x_1-\left(1-\sigma_{\min }\right) x}{1-\left(1-\sigma_{\min }\right) t}
$$
则对于$t \in [0, 1]$, 与$u_t\left(x \mid x_1\right)$ 对应的条件流(Conditional Flow)被定义为:
$$
\psi_t\left(x\right)=(1-(1-\sigma_{\text{min}})t)x + tx_1
$$
看起来这个就像对$x$ 和$x_1$ 的线性插值.
接着带入到$\mathcal{L}_{\mathrm{CFM}}(\theta)$ 中, 最终化简后可得:
$$
\mathcal{L}_{\mathrm{CFM}}(\theta)=\mathbb{E}_{t, q\left(x_1\right), p\left(x_0\right)}\left\Vert v_t\left(\psi_t\left(x_0\right)\right)-\left(x_1-\left(1-\sigma_{\min }\right) x_0\right)\right\Vert ^2
$$
当$\sigma_{\min} \rightarrow 0$ 的时候, 似乎有$u_t(x \mid x_1) = x_1 - x_0$, 嗯… 这个结果似乎也有一些眼熟… 这不是Rectified Flow的向量场形式吗?
此时, 条件流$\psi_t$ 实际上是$p_0(x \mid x_1), p_1(x \mid x_1)$ 之间最优传输的位移映射. 在这种视角下, OT Path对应的粒子运动轨迹始终沿直线:
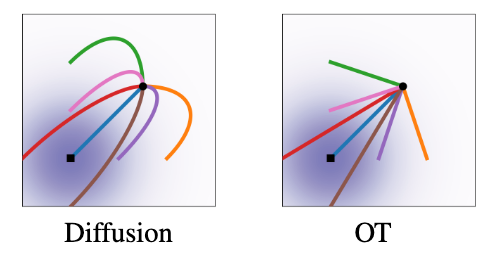
Diffusion Path对应的粒子运动轨迹则有可能冲过最终样本, 但是OT的则不会. Flow Matching和Rectified Flow得出了相同的结论.
对Diffusion Patch对应的Conditional Score Function($\nabla \log{p_t(x \mid x_1)}$)和OT Path的Conditional VF进行可视化:

蓝色代表大的值, 红色代表小的值. 可以发现:
- Diffusion Path: 速度场分布, 方向都随时间改变. 所以粒子运动服轨迹应该呈曲线.
- OT Path: 速度场方向恒定, 都指向终点, 只是不同的时刻对应的速度场大小不同. 所以粒子运动轨迹应该呈直线.
因此相较于Diffusion Path, OT Path具有更稳定的方向与更高效的向量场, OT Path是更容易训练的.
注意, 上述直线只是理想情况下训练出来的速度场对应的粒子运动轨迹!!! 实际学习到的路径并不是始终是直线!!!
下面选了几个ImageNet-64的Case:
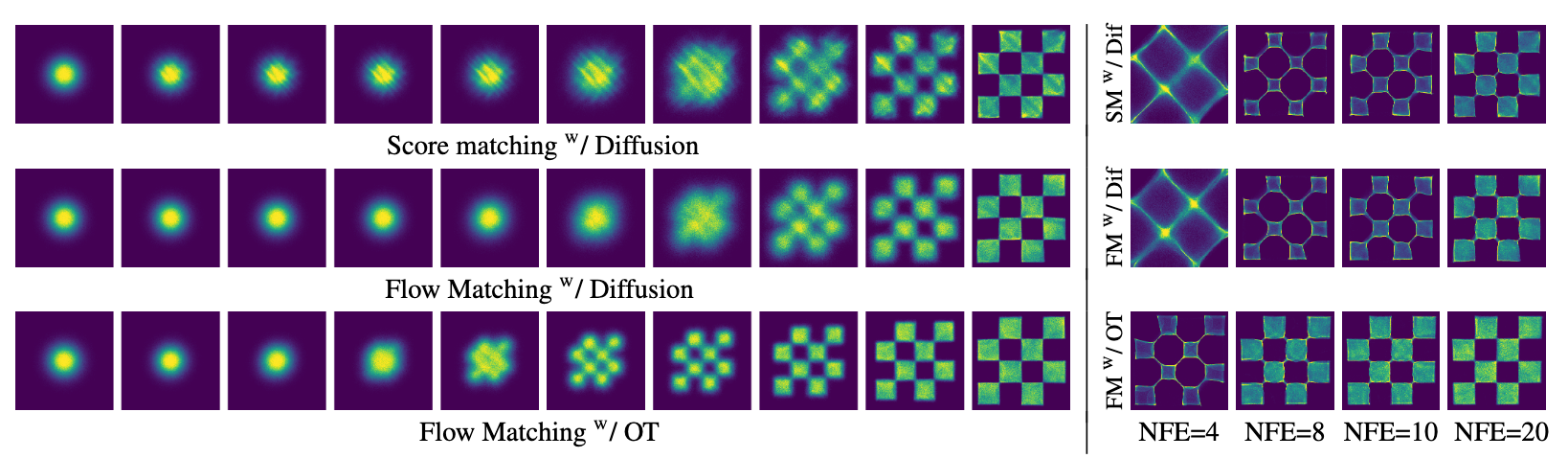
发现OT Path比其他的方法更早生成能看得过去的样本(左图), 并且在推理次数比较少的情况下能获得更好的质量(右图).
Recommended
- 强烈推荐看一下: 零推导理解Diffusion和Flow Matching - 王峰的文章 - 知乎, 这篇文章用几何的方式直接推导出了DDPM, DDIM, Flow Matching的形式, 并直观体现出它们的核心差异.
- Meta出的官方解读: Flow Matching Guide and Code, 论文里的一些图对于理解Flow Matching中提到的概念有很大帮助.
- 抽象文章名系列:
- 关于Loss: 扩散模型中,Flow Matching的训练方式相比于 DDPM 训练方法有何优势? - CW不要無聊的風格的回答 - 知乎.
- B站UP童发发:
Summary
总结感觉该写的在Rectified Flow里都写的差不多了, 这里就少写点.
DDIM, EDM都可以看做是Flow Matching框架下的一种特殊形式.
与同期工作Rectified Flow撞车也是一件非常有意思的事. 如果只是考虑工程上的话, 有了Flow Matching以后, 感觉可以绕过之前Diffusion Model的学习老路, 直接来学Flow Matching了.
