Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow
- 论文: Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow, ICLR 2023.
- 代码: GitHub - gnobitab/RectifiedFlow: Official Implementation of Rectified Flow (ICLR2023 Spotlight).
- 知乎讲解(一作): [ICLR2023] 扩散生成模型新方法:极度简化,一步生成 - XCLiu的文章 - 知乎.
Rectified Flow
Learning Transport Mapping
对于很多的无监督任务, 都可以被统一为建模两个分布之间的运输过程:
- 如GAN / VAE等生成类模型中建模的, 往往是建模一个简单的已知的分布到一个复杂的原始数据分布之间的关系.
- 所有的Domain Transfer Method, 例如Image-to-Image Translation, Style Transfer, Domain Adaption等任务, 都是在建模两个分布之间的转移关系.
因此, 将上述任务统一建模两个分布之间的运输过程. 形式化定义如下.
对于观测到的两个分布$\pi_0, \pi_1 \in \mathbb{R}^d$ , 需要找到一个运输映射$T: \mathbb{R}^d \rightarrow \mathbb{R}^d$, 能够使得在数据接近无限的情况下, 当$Z_0 \sim \pi_0$时, 有$Z_1 :=T(Z_0) \sim \pi_1$.
Rectified Flow将$X_0$ 转换为$X_1$ 的过程建模为一个定义在时间$t \in [0, 1]$ 上的常微分方程(ODE):
$$
\mathrm{d} Z_t=v\left(Z_t, t\right) \mathrm{d} t
$$
该过程将$Z_0 \sim \pi_0$ 转换为$Z_1 \sim \pi_1$. 对于这个转换过程, $X_0$ 为起点, $X_1$ 为终点. 转换过程中对应的向量场 $v: \mathbb{R}^d \rightarrow \mathbb{R}^d$ 被作者设置为使$X_0$ 遵循$X_1 - X_0$ 的方向尽可能沿直线移动的向量场.
这个向量场$v$ 就像河流中的水流一样, 可以将任意$X_t$ 位置的小船随着河流推至目的地$X_1$.
上述目标通过一个简单的MSE Loss来学习到:
$$
\min _v \int_0^1 \mathbb{E}\left[\left\Vert\left(X_1-X_0\right)-v\left(X_t, t\right)\right\Vert^2\right] \mathrm{d} t, \quad \text { with } \quad X_t=t X_1+(1-t) X_0
$$
其中$X_t$ 为$X_0, X_1$ 之间的线性插值, 它会遵循ODE $\mathrm{d}X_t = (X_1 - X_0) \mathrm{d}t$. 需要注意的是, 它是Non-Causal的, 即$X_t$ 需要依赖终点$X_1$ 才可得知, 但是$X_1$ 在推理时又是未知的. 不过它可以通过用$X_1 - X_0$ 训练向量场$v$, 可以在不知道$X_1$ 的情况下将$X_t$ 推至$X_1 - X_0$ 的插值路径上, 从而实现把这个过程变成Causal的.
在实际推理时, $X_0 \sim \pi_0$ 往往是咱们已知的简单分布, 进一步用欧拉法采样就可以得到需要的$X_1$ 了. 或者再更换一些其他的高阶采样方法也是可以的, 只不过会引入更多的计算量. 假设步长为$\frac{1}{N}$, 则有:
$$
\hat{Z}_{t+\frac{1}{N}} = \hat{Z}_t + v(\hat{Z}_t, t) \cdot \frac{1}{N}
$$
特别的, 对于一种特殊的单步情况, 有$z_1 = z_0 + v(z_0, 0)$.
对, 如果只谈方法的话就这么简单, Rectified Flow介绍完了. 本文到此结束(×).
Flows Avoid Crossing
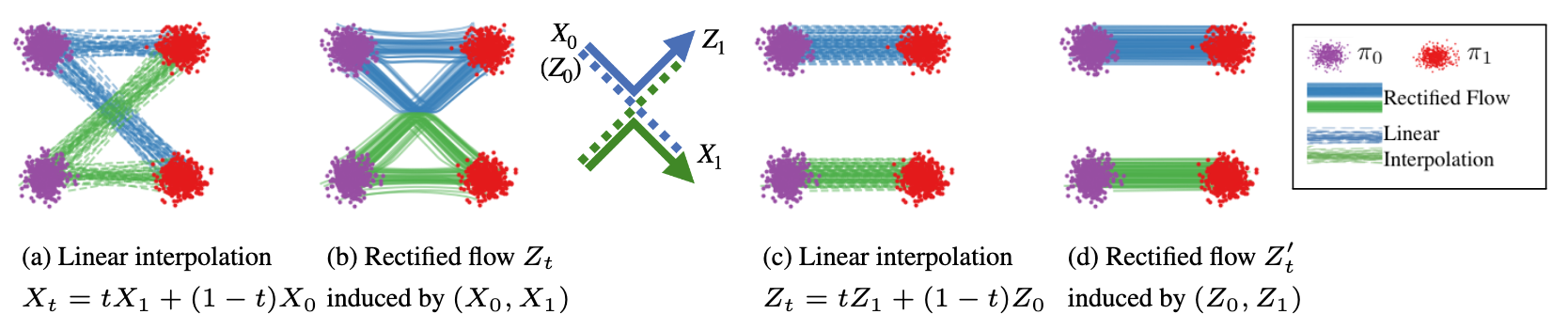
Rectified Flow核心在于, 对于定义好的ODE $\mathrm{d} Z_t=v\left(Z_t, t\right) \mathrm{d} t$, 应该是解存在且唯一的, 且对于时间$t \in [0, 1)$ 在场内的两条轨迹都不能交叉. 即不存在位置$z \in \mathbb{R}^d$ 和时间$t \in [0, 1)$ 使得两条路径能在同一时刻$t$ 以不同方向穿过位置$z$, 如果出现了, 则ODE的解就不是唯一的了.
换句话说, 在向量场$v$ 中, 对于任意初始点$(z_0, t_0)$, 存在轨迹$z(t)$, 该轨迹在任意时刻$t$ 的位置是确定且唯一的, 并且取决于初始信息$(z_0, t_0)$.
对于$X_0 \sim \pi_0, X_1 \sim \pi_1$, 当对$X_1, X_0$ 进行线性插值时, 其插值$X_t$ 可能导致出现轨迹的交叉, 从而导致它的Non-Causal, 如上图 (a). 即依赖于未来的关系, 已知$(X_0, X_1)$ 的全局配对关系才能确定轨迹, 否则会出现 (a) 中的$X_0$ 与上面和下面的$X_1$ 匹配都可以的情况.
因此, Rectified Flow通过对ODE的建模, 利用ODE唯一解的性质, 来避免了这种交叉轨迹的情况, 如上图 (b). 可以将线性插值$X_t$ 视为是连接$\pi_0, \pi_1$ 之间的公路, 而Rectified Flow的学习到的向量场$v$ 在无需依赖未来信息的条件下迫使$X_0$ 的点按照向量场中确定路径移动到$X_1$, 从而得到一组确定的匹配关系$(Z_0, Z_1)$. 因此向量场$v$ 更像是在引导车辆沿哪条路走的交通拥堵情况. 并且$v$ 在学习的时候, 并不关心$(X_0, X_1)$ 全局上是如何配对的, 它只关心局部角度学到的向量场是什么样的, 所以它是Causal的.
在进行过一次Rectified Flow后, 得到的新的匹配对$(Z_0, Z_1)$ 已经是两两匹配的, 如图 (c), (d)所示. 该性质在下个小节会提到.
Straight Line Flows Yield Fast Simulation
通过对上面的内容观察发现, 虽然定义了Rectified Flow, 但是它的向量场引导的粒子轨迹仍然不是一条直线.
再回顾下之前的Non-Causal. 如果知道了$X_0, X_1$ 之间的配对关系, 是不是就能通过一步采样, 让模型走直线, 直接通过$X_0$ 找到对应的$X_1$? 当时的问题在于, 它是Non-Causal的. 我们需要的是Causal的向量场, 所以这时的向量场$v$ 只能基于$X_0, X_1$ 之间构造的随机两两匹配对进行训练.
但是, 我们在进行过一次Rectified Flow后, $X_0, X_1$ 之间的配对关系在第一次的Rectified Flow作用下, 已经能够拿到有先验的匹配对了, 即每个$X_0$ 已经有了确定匹配的$X_1$ 作为目标! 有了基于1-ReFlow的新匹配对$(Z_0^1, Z_1^1)$, 再次进行Rectified Flow, $Z_0^1$ 会沿着更”直”的轨迹运动到$Z_1^1$! 所以作者提出了ReFlow.
如果$\boldsymbol{Z}=\operatorname{RectFlow}\left(\left(X_0, X_1\right)\right)$ 代表从$(X_0, X_1)$ 得到的Rectified Flow, 对每次ReFlow的结果可以进行叠叠乐, 递归调用得到:
$$
\boldsymbol{Z}^{k+1}=\operatorname{RectFlow}\left(\left(Z_0^k, Z_1^k\right)\right)
$$
其中$(Z_0^0, Z_1^0) = (X_0, X_1)$, $\boldsymbol{Z}^{k}$ 为第$k$ 个Rectified Flow.
多次ReFlow后的效果:
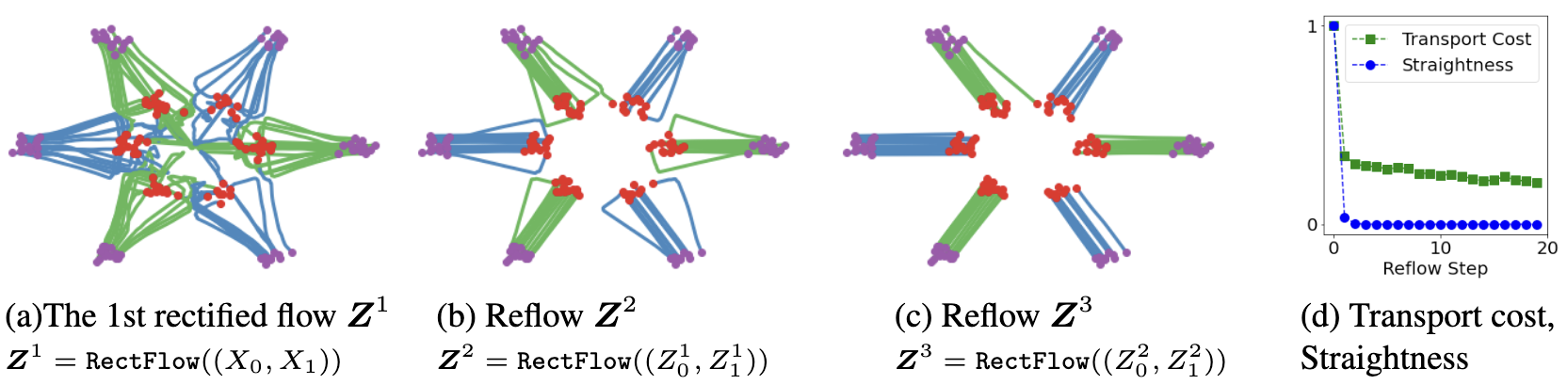
这种ReFlow不但降低了Transport Cost, 还对ReFlow中的路径进行了”拉直”, 越多次的ReFlow, 粒子的轨迹就越”直”. 不负责任的说, 如果你想要4-ReFlow, 5-ReFlow… 甚至你可以一直ReFlow下去…
我看论文的时候就感觉, 实际应用过程中$v$ 不可能学的非常理想, 所以每次获得的$Z_1^k$ 通常与希望得到的$X_1$ 是有偏差的, 这就导致ReFlow多次会产生误差累计, 这个问题作者本人也提到了, 所以不建议进行过多的ReFlow堆叠.
Distillation
经过$k$ 次Rectified Flow $\boldsymbol{Z}^{k}$ 后, 可以直接将多次ReFlow后得到的$(Z_0^k, Z_1^k)$ 的匹配关系蒸馏到NN $\hat{T}$ 中, 从而实现一步生成的$\hat{T}(z_0) \approx z_0 + v(z_0, 0)$.
在蒸馏的时候, 只需要将ReFlow的训练目标中的$t$ 设置为0, 即如下Loss来训练$\hat{T}$:
$$
\mathcal{L} = \mathbb{E}\left[\left\Vert\left(Z_1^k-Z_0^k\right)-v\left(Z_0^k, 0\right)\right\Vert^2\right]
$$
但是注意, ReFlow和Distillation是完全不同的, 因为Distillation只学习$(Z_0^k, Z_1^k)$ 之间的映射关系(即$t=0, t=1$), 而ReFlow则在优化$Z_0^k \rightarrow Z_1^k$ 之间的整个过程(即$t \in [0, 1)$ 之间).
综上, Rectified Flow的算法流程伪代码如下:

Notebook Tutorial
由于作者提供了Notebook方便大家了解Rectified Flow的匹配过程, 所以咱们也瞅瞅Rectified Flow是怎么实现的, 超级简单(这也是为什么很多生成类模型想换Rectified Flow, 因为它工程上便于实现):
如果你不能科学上网, 应该看不到Open in Colab的图标.
如果想看作者在论文中的例子(就是两个类的例子), 可以将Notebook中第一个codeblock中的代码做如下改动(直接复制粘贴就行, 只更改了数据的初始化方式):
import torch
import numpy as np
import torch.nn as nn
from torch.distributions import Normal, Categorical
from torch.distributions.multivariate_normal import MultivariateNormal
from torch.distributions.mixture_same_family import MixtureSameFamily
import matplotlib.pyplot as plt
import torch.nn.functional as F
D = 10.
M = D+5
VAR = 0.3
DOT_SIZE = 4
COMP = 2
initial_mix = Categorical(torch.tensor([1/COMP for i in range(COMP)]))
initial_comp = MultivariateNormal(torch.tensor([[-D * np.sqrt(3) / 2., -D / 2.], [-D * np.sqrt(3) / 2., D / 2.]]).float(), VAR * torch.stack([torch.eye(2) for i in range(COMP)]))
initial_model = MixtureSameFamily(initial_mix, initial_comp)
samples_0 = initial_model.sample([10000])
target_mix = Categorical(torch.tensor([1/COMP for i in range(COMP)]))
target_comp = MultivariateNormal(torch.tensor([[D * np.sqrt(3) / 2., - D / 2.], [D * np.sqrt(3) / 2., D / 2.]]).float(), VAR * torch.stack([torch.eye(2) for i in range(COMP)]))
target_model = MixtureSameFamily(target_mix, target_comp)
samples_1 = target_model.sample([10000])
print('Shape of the samples:', samples_0.shape, samples_1.shape)
plt.figure(figsize=(4,4))
plt.xlim(-M,M)
plt.ylim(-M,M)
plt.title(r'Samples from $\pi_0$ and $\pi_1$')
plt.scatter(samples_0[:, 0].cpu().numpy(), samples_0[:, 1].cpu().numpy(), alpha=0.1, label=r'$\pi_0$')
plt.scatter(samples_1[:, 0].cpu().numpy(), samples_1[:, 1].cpu().numpy(), alpha=0.1, label=r'$\pi_1$')
plt.legend()
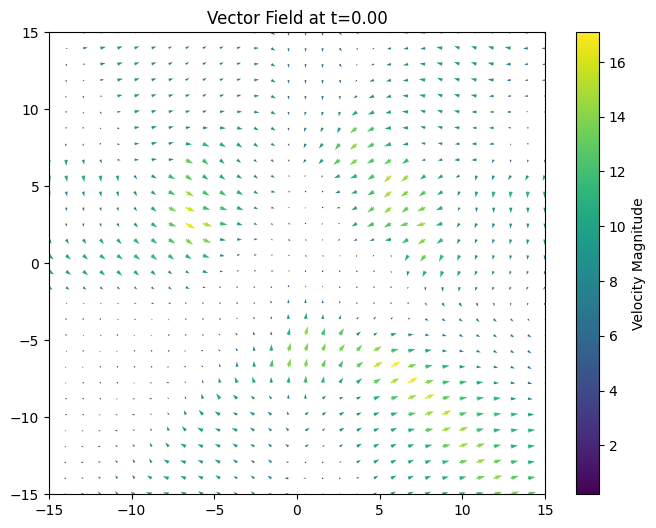
plt.tight_layout()如果对学习到的ODE(向量场)长什么样感到好奇, 可以用如下代码可以做出向量场:
The following code is supported by DeepSeek.
def plot_vector_field(rectified_flow, t=0.0, n_grid=30):
"""绘制指定时间t的二维向量场"""
# 生成网格点
x = np.linspace(-15, 15, n_grid)
y = np.linspace(-15, 15, n_grid)
X, Y = np.meshgrid(x, y)
# 转换为PyTorch张量
grid_points = torch.tensor(np.stack([X.ravel(), Y.ravel()], axis=1), dtype=torch.float32)
time_points = torch.ones((grid_points.shape[0], 1)) * t
# 模型预测向量场
with torch.no_grad():
vectors = rectified_flow.model(grid_points, time_points).numpy()
# 转换为绘图格式
U = vectors[:, 0].reshape(n_grid, n_grid)
V = vectors[:, 1].reshape(n_grid, n_grid)
# 绘制向量场
plt.figure(figsize=(8, 6))
plt.quiver(X, Y, U, V,
np.sqrt(U**2 + V**2), # 用颜色表示速度大小
cmap='viridis',
angles='xy',
scale_units='xy',
scale=25, # 调整箭头密度
width=0.003)
plt.colorbar(label='Velocity Magnitude')
plt.title(f'Vector Field at t={t:.2f}')
plt.xlim(-15, 15)
plt.ylim(-15, 15)
plt.show()下面放一些作者Notebook中的模型训练得到的向量场, t=0.0:
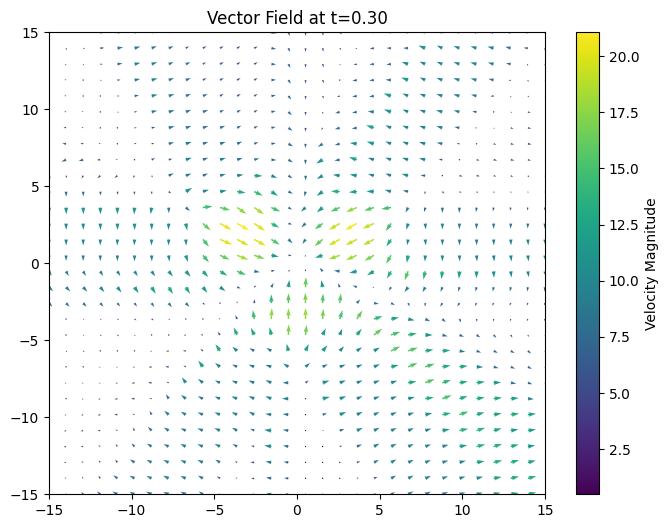
t=0.3:
t=0.8:
这里留个课后作业, 感兴趣的话还可以画下Notebook里面2-ReFlow的向量场, 应该是个比较直的.
Summary
Optimal Transport和Diffusion Model其实有千丝万缕的联系. Flow-based Model在建模时都是从最优传输视角出发的.
而Rectified Flow作为Flow-based Generative Model, 通过NN学习一个ODE, 能更快完成生成类任务. 工程实现简单, 受到了大家的青睐, 例如Stable Diffusion 3中就采用了Rectified Flow作为架构. 生成类模型想绕开Rectified Flow几乎是不太可能的. 不得不说, 虽然这些简洁的工作背后隐藏着更深的理论支撑就是了, 但是在大家的眼里总是便于理解, 简单且有效.
非常有趣的是, 同期的另一篇工作Flow Matching和Rectified Flow思路是一样的, 笔记我写的差不多了, 回头咱们再讲.
话说回来, 这么一看感觉DDIM显得像个小丑… 太复杂了, 甚至还不如ReFlow直接用Euler Sampling来的实在.
当然, 我数学功底不太好, 所以也省略了原文中诸多细节, 尤其是ReFlow的一些性质和推导过程, 我都略过了.
最后, 需要纠正一个误区. Rectified Flow并非整条粒子的轨迹都是直线. 因为向量场$v$ 肯定不会学的很理想嘛, 所以不可能向量场的每处对$X_1$ 的估计都是准确的, 不可能让向量场的所有处都能使粒子准确的推向$X_1$. 在实际推理采样的时候, 运用欧拉法采样的Step大于1时, 得到的轨迹实际上是多次折现近似的曲线, 这篇ICLR 2025的文章也能佐证这一观点.

