本文前置知识:
OneRel: Joint Entity and Relation Extraction with One Module in One Step
本文是论文OneRel:Joint Entity and Relation Extraction with One Module in One Step的阅读笔记和个人理解, 论文来自AAAI 2022.
Basic Idea
现有的RTE方法经常将其分解为几个步骤, 使得其比较好抽取. 然而, 这种分解常常忽视了三元组是互相关联的整体, 当前方法常存在误差累计和信息冗余的问题. 例如:
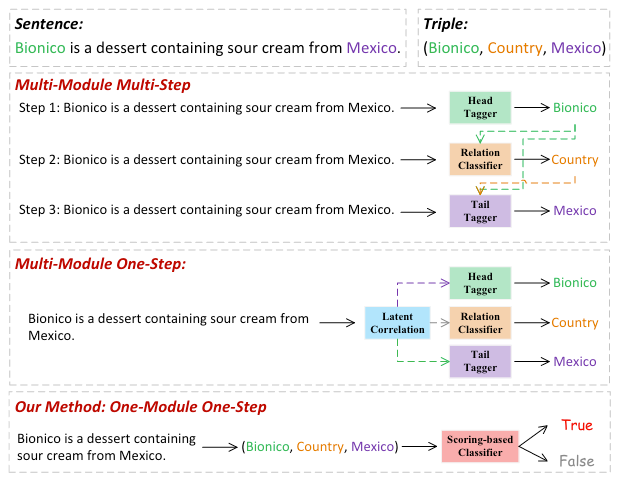
它们分别对应着:
在本文中, 作者希望将三元组抽取视为一种细粒度三元组分类任务, 用单模单步的方式解决上述问题.
OneRel
Task Definition
对于给定的$L$ 个Token的句子$\mathcal{S}=\set{w_1, w_2, \dots, w_l}$ 以及$K$ 个已经定义好的关系$\mathcal{R}=\set{r_1, r_2, \cdots, r_K}$, RTE的目标为识别出句子$\mathcal{S}$ 中的所有$N$ 个三元组$\mathcal{T}=\left\{\left(h_{i}, r_{i}, t_{i}\right)\right\}_{i=1}^{N}$, $h_{i}, t_i$ 分别为由连续Tokens构成的Span而组成的头实体和尾实体.
Relation Specific Horns Tagging
作者设计了一个分类器, 来对$(w_{i,}r_{k,}w_j)$ 所有可能的组合来做分类, 也就是维护一张$\boldsymbol{M}^{L \times K \times L}$ 的三维表存储分类结果.
Tagging
作者设计标签时, 以BIE(Begin, Inside, End)为出发点.
如果将头实体和尾实体的BIE组合则需要9种标签, 实际上不需要这么多.
作者使用3种有效标签, 来标注头尾实体并建立二者的关联:
- HB - TB: 标注头实体的头和尾实体的头.
- HB - TE: 标注头实体的头和尾实体的尾.
- HE - TE: 标注头实体的尾和尾实体的尾.
- NULL: 啥也不是.
例如:
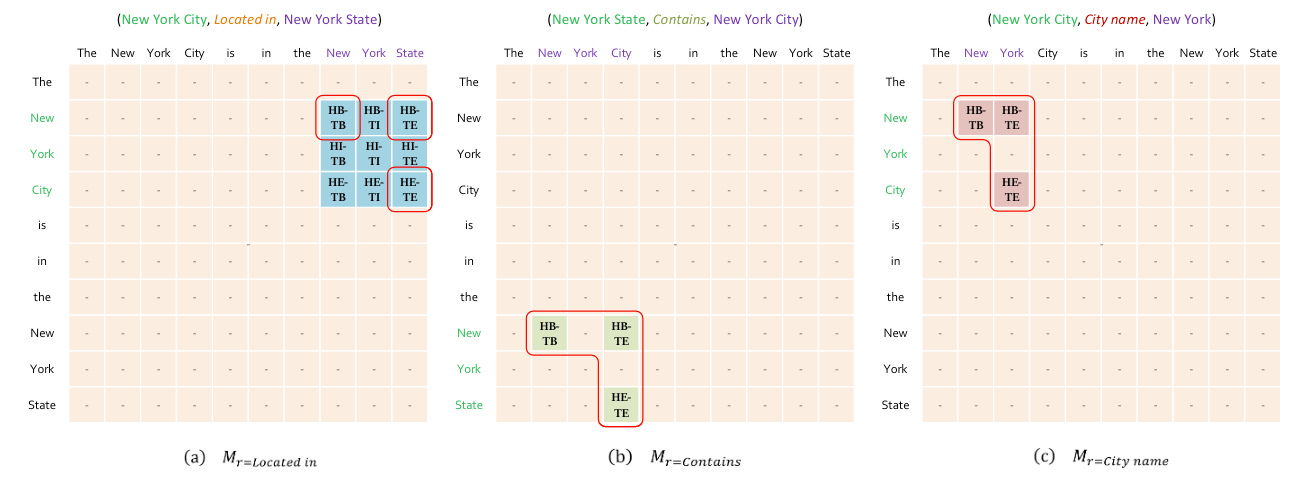
由于它构成三元组的形状只需要三个支点, 因此也被作者称为关系特化的山羊角标注法(Rel - Spec Horns Tagging).
作者认为这种标注策略有三好:
- 用3种标签而不是9种缩小了搜索空间.
- 稀疏的表$\boldsymbol{M}$ 有大量的负样本.
- $\boldsymbol{M}$ 的稀疏性保证了解码速度.
Decoding
解码的判定逻辑就是按照顺序往下找:
- 找HB - TB.
- 如果同一行的下一个标签是HB -TE, 就向下找.
- 找到HE - TE, 形成一对三元组.
Scoring - based Classifier
首先Encoder的特征抽取部分大家都是老生常谈了, 每个Token$d$ 维的Token Embedding$\boldsymbol{e}_{i}$ 可以由BERT得到:
$$
\left\{\boldsymbol{e}_{1}, \boldsymbol{e}_{2}, \ldots, \boldsymbol{e}_{L}\right\}=B E R T\left(\left\{\boldsymbol{x}_{1}, \boldsymbol{x}_{2}, \ldots, \boldsymbol{x}_{L}\right\}\right)
$$
$\boldsymbol{x}_{i}$ 为每个Token的输入表示.
接着, 作者按照作者的原思路, 继续穷举所有句子中可能的$\left(\boldsymbol{e}_{i}, \boldsymbol{r}_{k}, \boldsymbol{e}_{j}\right)$ 组合($\boldsymbol{r}_{k}$ 为随机初始化的关系Embedding), 用神经网络弄一个三元组打分分类器, 判定$\left(\boldsymbol{e}_{i}, \boldsymbol{r}_{k}, \boldsymbol{e}_{j}\right)$ 是否成立就好. 但是作者认为这样有两个缺陷:
- 简单的分类器不能充分使得实体和关系间的交互, 且难以建模三元组的结构化信息.
- 做$L \times K \times L$ 次分类很耗时.
所以作者提出了另一种思路, 受启发于KGE里的HOLE的打分函数:
$$
f_{r}(h, t)=\boldsymbol{r}^{T}(\boldsymbol{h} \star \boldsymbol{t})
$$
其中$\boldsymbol{h}, \boldsymbol{t}$ 分别为头尾实体的表示, $\star$ 为循环卷积操作. HOLE挖掘了两实体间的关联. 在作者的模型中, 将$\star$ 重定义为拼接后非线性投影:
$$
\boldsymbol{h} \star \boldsymbol{t}=\phi\left(\boldsymbol{W}[\boldsymbol{h} ; \boldsymbol{t}]^{T}+\boldsymbol{b}\right)
$$
其中$\boldsymbol{W} \in \mathbb{R}^{d_{e} \times 2d}$, $\boldsymbol{b}$ 为可训练参数, $d_e$ 代表头尾实体对表示的维度, $[;]$ 为拼接操作, $\phi(\cdot)$ 为ReLU激活函数. 作者认为这样有三好:
- 新设计的打分函数可以和Encoder无缝衔接.
- 从实体特征到实体对特征维度可以由$\boldsymbol{W}$ 改变.
- 非对称性, 即$[\boldsymbol{h} ; \boldsymbol{t}] \neq[\boldsymbol{t} ; \boldsymbol{h}]$.
然后用所有关系表示$\boldsymbol{R} \in \mathbb{R}^{d_{e}\times 4K}$ 同时计算所有Token对$(w_i, w_j)$ 所对应的$(w_{i,}r_{k,}w_j)_{k=1}^K$, $4$ 为分类标签, 所以作者的方法最后归结为:
$$
\boldsymbol{v}_{\left(w_{i}, r_{k}, w_{j}\right)_{k=1}^{K}}=\boldsymbol{R}^{T} \phi\left(\operatorname{drop}\left(\boldsymbol{W}\left[\boldsymbol{e}_{i} ; \boldsymbol{e}_{j}\right]^{T}+\boldsymbol{b}\right)\right)
$$
其中$\boldsymbol{v}$ 为得分向量, $\operatorname{drop}(\cdot)$ 为Dropout.
尽管计算方式不怎么稀奇, 但是从KGE和三元组分类这个角度出发来解释倒是有点新颖.
作者认为, 由于把表分类矩阵设为$\boldsymbol{R} \in \mathbb{R}^{d_{e}\times 4K}$, 一次性可以处理所有关系, 所以处理步数实际上为$L \times 1 \times L$, 要强于TPLinker.
这个地方我也不是太确定, 对于作者的说法, 我寻思这不还是$L \times K \times L$ 的填表分类么?
TPLinker使用$2|R|+1$的表来标注(EH-ET只使用了一张), 而OneRel使用$|R|$ 的表来标注, 因为OneRel在标签设计上规避了不同类型标签重叠的可能性. 我认为这种说法要更具有说服力.
最后把得分向量做个Softmax:
$$
P\left(\mathrm{y}_{\left(w_{i}, r_{k}, w_{j}\right)} \mid \mathcal{S}\right)=\operatorname{Softmax}\left(\boldsymbol{v}_{\left(w_{i}, r_{k}, w_{j}\right)}\right)
$$
训练损失函数为多分类交叉熵:
$$
\mathcal{L}_{\text {triple }}=-\frac{1}{L \times K \times L} \times \sum_{i=1}^{L} \sum_{k=1}^{K} \sum_{j=1}^{L} \log P\left(\mathrm{y}_{\left(w_{i}, r_{k}, w_{j}\right)}=g_{\left(w_{i}, r_{k}, w_{j}\right)} \mid \mathcal{S}\right)
$$
其中$g_{(w_{i,}r_{k}, w_{j})}$ 为Golden Label.
Experiments
仍然是NYT, NYT*, WebNLG, WebNLG* 四个数据集, 统计信息如下:
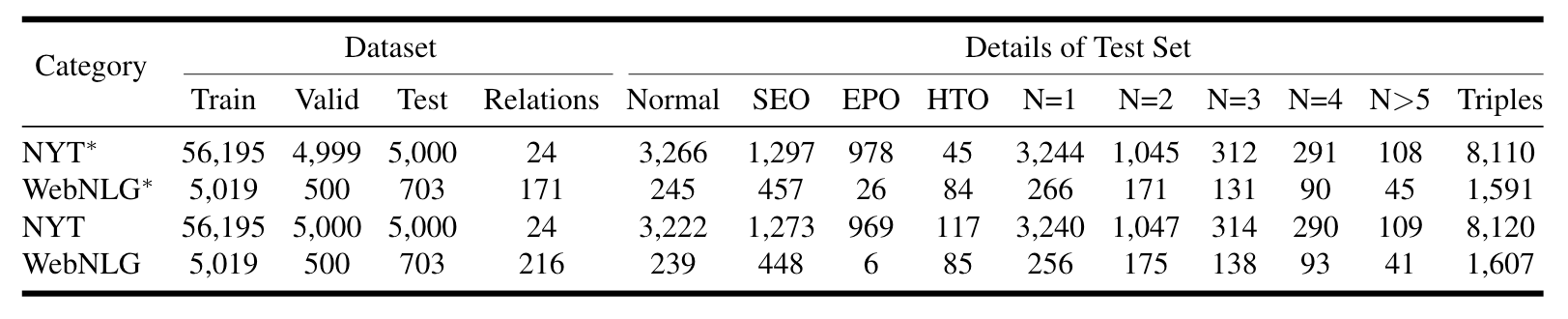
Main Results
OneRel在四个数据集上的部分匹配和精准匹配结果如下:
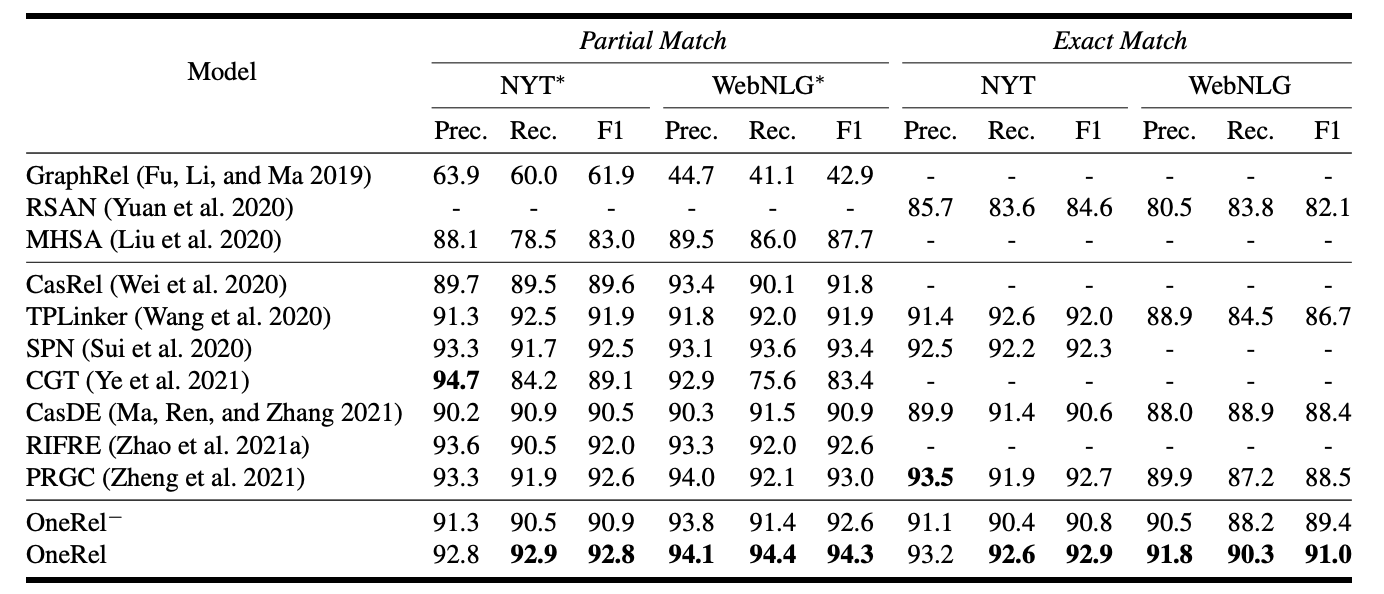
OneRel - 指的是将分类器替换成$\boldsymbol{W}[\boldsymbol{e_i};\boldsymbol{r_{k}};\boldsymbol{e_j}]+\boldsymbol{b}$, 也就是使用简单的线性分类器. OneRel完全体达到了现在的SOTA, 看起来OneRel - 和完全体还是有一定差距.
Detailed Results on Complex Scenarios
OneRel在不同类型三元组的表现如下:
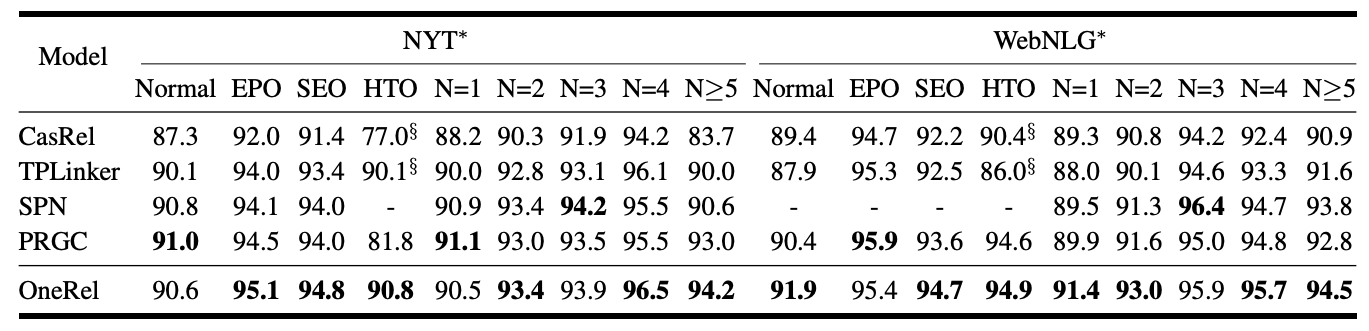
OneRel在大多数情况下表现良好.
Results on Different Sub - tasks
按照预测三元组的不同部分区分, 结果如下:
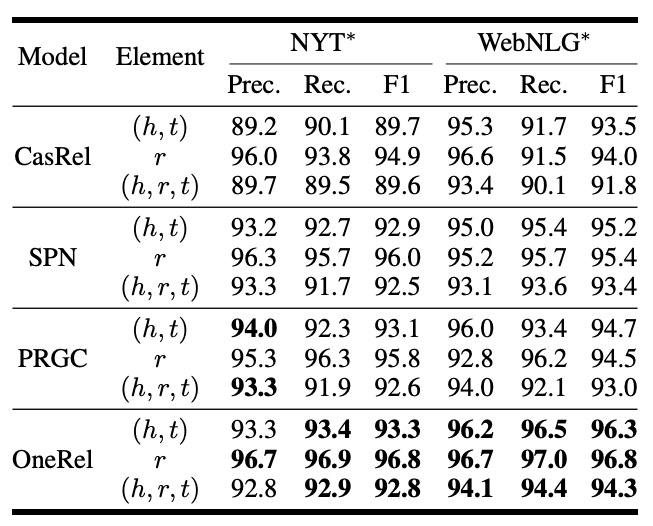
OneRel在关系预测上比之前的模型都要强挺多, 实体预测也不弱, 在NYT*上的实体预测能力和SPN相当.
Model Efficiency
论文在前面说了OneRel的速度比TPLinker快, 在这里作者做了个实验证明下:
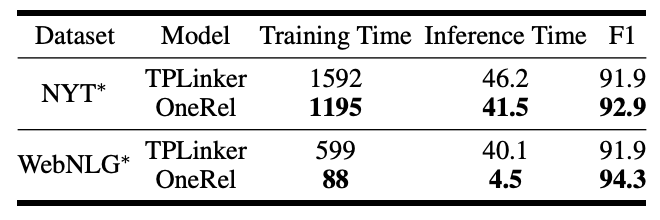
WebNLG*上差距挺明显的, NYT*上差距并不是特别大.
我猜这里实现差异因素占了一大部分, 当时TPLinker跑关系是用的循环然后再运算的, 而OneRel直接做的并行张量运算. NYT*的关系数量比WebNLG*少得多, 所以二者相差也不大. 我更倾向于OneRel的效率高原因是因为用的表少.
Topology Structure of Relations
既然往KGE靠边了, 使用了关系Embedding, 自然而然就能想到对它做可视化来证明模型有效. 下面是NYT上24中关系在T - SNE下的降维可视化图:
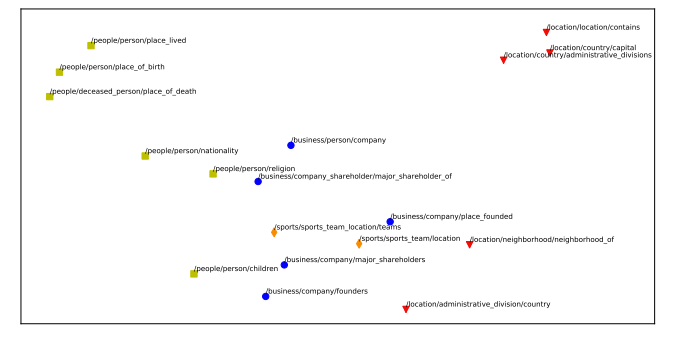
从图上来看确实语义相似的Embedding靠的比较近. 不过这种可视化图也只能从直觉上显示性能, 并不是绝对的.
Summary
总体来说, OneRel其实没有什么亮点, 实质上属于一种填表式RTE模型, 文章中所称的单模单步有点牵强. 这回OneRel了, 但是没有很OneRel.
一般来说, Table - Filling based model的Decoder部分会设计的比较简单, 真正发挥作用的是如何建立表标签.
OneRel相较于TPLinker来说, 相差并不大. 不用建立多张表, 使用了更精炼的标注策略, 当然也付出了相应的代价.
事实上, 需要在每个token后多添加一个
[unused1]来避免单个token的实体抽取问题. 这点作者在文章中未提起过.

