A Novel Cascade Binary Tagging Framework for Relational Triple Extraction
本文是论文A Novel Cascade Binary Tagging Framework for Relational Triple Extraction的阅读笔记和个人理解, 论文来自ACL 2020.
Basic Idea
在面向三元组抽取设计的模型中, 少有模型能够解决多重关系三元组重叠问题, 这类三元组往往是共享实体的. 例如:
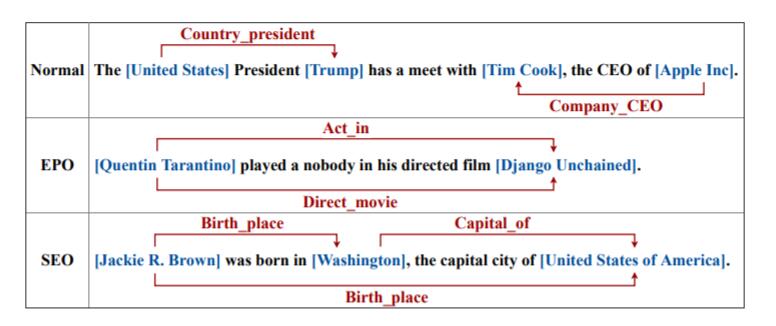
作者认为有两种三元组重叠现象发生:
- EPO(Entity Pair Overlap): 实体对重叠是指实体对之间具有多种关系, 这些三元组共享相同的实体.
- SEO(Single Entity Overlap): 单实体重叠是指有单个实体被多个三元组共享, 如例子中的
Washington.
基于重叠问题, 作者提出将关系视为句间实体的映射, 以此解决重叠问题.
CasRel
CasRel与先前的模型不同, 它希望将目标函数指定在Triple Level, 而非像先前的做法将三元组抽取的过程拆开, 并分别设立目标函数.
在数据集$D$ 中已标注的句子$x_i$ 中, 对于给定的三元组$T_j = \set{(s,r,o)}$, 作者希望最大化三元组在给定句子下的概率:
$$
\begin{aligned}
& \prod_{j=1}^{|D|}\left[\prod_{(s, r, o) \in T_{j}} p\left((s, r, o) \mid x_{j}\right)\right] \\
=& \prod_{j=1}^{|D|}\left[\prod_{s \in T_{j}} p\left(s \mid x_{j}\right) \prod_{(r, o) \in T_{j} \mid s} p\left((r, o) \mid s, x_{j}\right)\right] \\
=& \prod_{j=1}^{|D|}\left[\prod_{s \in T_{j}} p\left(s \mid x_{j}\right) \prod_{r \in T_{j} \mid s} p_{r}\left(o \mid s, x_{j}\right) \prod_{r \in R \backslash T_{j} \mid s} p_{r}\left(o_{\varnothing} \mid s, x_{j}\right)\right]
\end{aligned}
$$
第一步到第二步是条件概率, 第二步到第三步将$r$ 分为$s$ 应该有的关系 $r \in T_{j} \mid s$ 和$s$ 一定不会存在的关系$r \in R \backslash T_{j} \mid s$ 来考虑.
所有与$s$ 可能发生的关系, 都应该在句子中找到与之对应的$o$ , 如果$s$ 不可能存在$r$, 那么必然找不到对应的$o$, 因此就要有$o_{\varnothing}$ 存在, 即”Null” Object.
这样, 如果三元组存在, 就应该可以通过Subject在Relation下找到相应的Object, 也就是所谓的”映射关系“.
作者认为这样有三点好处:
- Triple Level的目标函数建立与最终评估方式是相符的.
- Triple Level的建模直接规避了实体如何被共享的问题.
- 第三步的拆解启发了模型的结构设计. 通过最大化$p\left(s \mid x_{j}\right)$训练Subject Tagger, 再在已知Subject的条件下最大化给定关系$r$ 的$p_{r}\left(o \mid s, x_{j}\right)$ 来训练Object Tagger, 关系便自然成为实体之间的映射函数.
BERT Encoder
对于句子$x_j$, BERT抽取它的特征. 令$\operatorname{Trans}(\mathbf{x})$ 为Transfomer Encoder Bolck, 将$N$ 层堆叠, 得到特征$\mathbf{h}_\alpha$:
$$
\begin{aligned}
\mathbf{h}_{0} &=\mathbf{S} \mathbf{W}_{s}+\mathbf{W}_{p} \\
\mathbf{h}_{\alpha} &=\operatorname{Trans}\left(\mathbf{h}_{\alpha-1}\right), \alpha \in[1, N]
\end{aligned}
$$
$\mathbf{S}$ 为句子的One Hot向量, $\mathbf{W}_s$ 为Subword的Embedding矩阵, $\mathbf{W}_p$ 为位置编码矩阵.
根据任务, 作者在这里只使用单句, 而非像BERT原文使用句子对.
Cascade Decoder
作者希望分两步抽取三元组:
- 首先从句子中抽取Subject.
- 然后在所有可能的关系$r$ 的条件下, 看是否有与Subject相对应的Object.
因此作者也设计了两相对应的模块.
Subject Tagger
简单的使用两个二分类器分别识别Subject的起始和结束位置, 对每个Token的对应位置都是两个二分类问题, 这个位置是不是起始位置? 是不是结束位置?
描述如下:
$$
\begin{array}{r}
p_{i}^{\text {start_s }}=\sigma\left(\mathbf{W}_{\text {start }} \mathbf{x}_{i}+\mathbf{b}_{\text {start }}\right) \\
p_{i}^{\text {end_s }}=\sigma\left(\mathbf{W}_{\text {end }} \mathbf{x}_{i}+\mathbf{b}_{\text {end }}\right)
\end{array}
$$
$p_{i}^{\text {start_s }}, p_{i}^{\text {end_s }}$ 分别为输入句子的第$i$ 个Token是否为Subject起始位置的概率和结束位置的概率.
其中$\mathbf{W}_{\text{start}}, \mathbf{W}_{\text{end}}$ 为权重矩阵, $\mathbf{b}_{\text {start }}, \mathbf{b}_{\text {end }}$ 为偏置, $\sigma$ 为Sigmoid函数.
得出的概率超过先设定好的阈值时, 便标记为1, 否则为0.
对于Subject $s$, 我们最大化如下概率:
$$
p_{\theta}(s \mid \mathbf{x})
=\prod_{t \in\{\text { start_s }, \text { end_s }\}} \prod_{i=1}^{L}\left(p_{i}^{t}\right)^{\mathbf{I}\left\{y_{i}^{t}=1\right\}}\left(1-p_{i}^{t}\right)^{\mathbf{I}\left\{y_{i}^{t}=0\right\}}
$$
$L$ 为句长, $\mathbf{I}\set{z} = 1$ 表示如果$z$ 为真则为1, 否则为0. $y_i^{\text {start_s }}, y_i^{\text {end_s }}$ 分别为Subject的起始结束位置二值化的Tag. $\theta$ 就是前面提到的Subject Tagger的参数.
由于一定会检测到多个Subject的Start和End, 作者遵循最近匹配原则, 即将最近的Start和End做匹配, 在区间内的Token标识为一个实体.
Subject Tagger如下图所示:
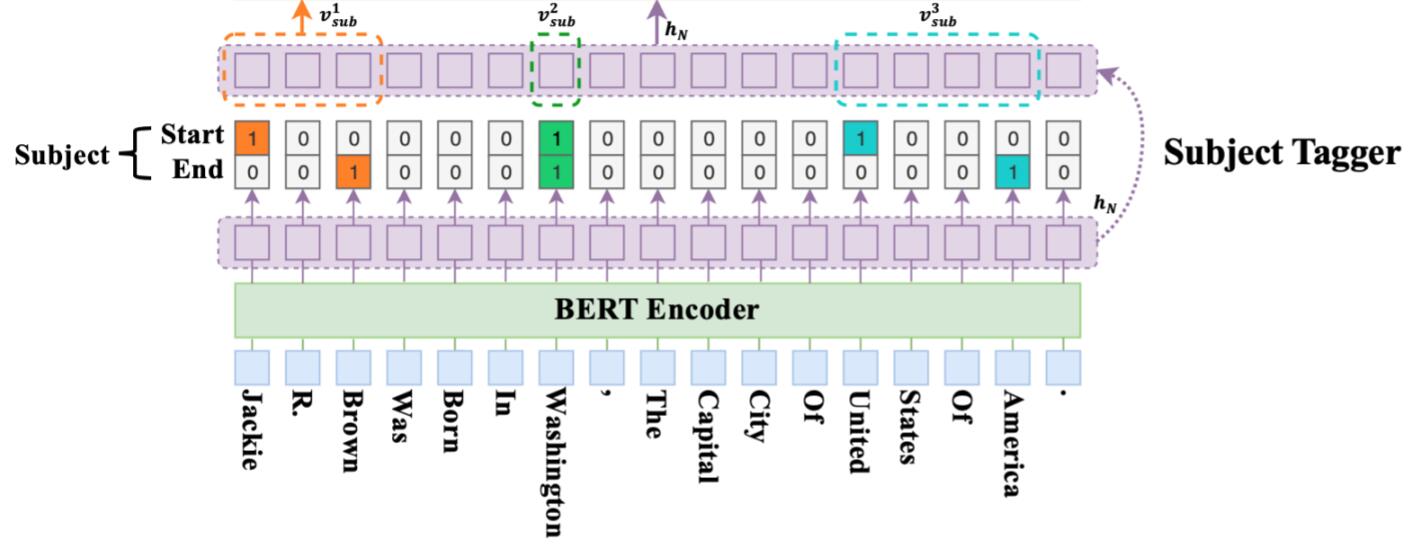
句子中的Token被BERT编码后, Subject Tagger能从中预测每个Token所对应的位置是否为Subject的起始位置, 结束位置. 在获取所有的起始结束位置后, 遵循最近匹配原则, 将最近的Start和最近的End匹配到一起, 区间内被视为一个Subject.
如图中以Jackle为起始, Brown为结束, Jackle R. Brown就被标识为一个Subject. Washington的起始和结束时同一个位置.
Relation - specific Object Taggers
关系特化的Object Tagger是一种比Subject Tagger更高阶的模块, 因为它是建立在Subject Tagger抽取出的Subject的基础之上的, 它的结构与Subject Tagger基本相同, 只是对关系做了特化处理, 即对每个关系都做给定Subject的Object抽取.
具体形式如下:
$$
\begin{array}{r}
p_{i}^{\text {start_o }}=\sigma\left(\mathbf{W}_{\text {start }}^{r}\left(\mathbf{x}_{i}+\mathbf{v}_{\text {sub }}^{k}\right)+\mathbf{b}_{\text {start }}^{r}\right) \\
p_{i}^{\text {end_o }}=\sigma\left(\mathbf{W}_{\text {end }}^{r}\left(\mathbf{x}_{i}+\mathbf{v}_{s u b}^{k}\right)+\mathbf{b}_{\text {end }}^{r}\right)
\end{array}
$$
$p_{i}^{\text {start_o }}, p_{i}^{\text {end_o }}$ 分别为输入句子的第$i$ 个Token是否为Object起始位置的概率和结束位置的概率. 这里作者简单的取了第$k$ 个Subject所有Token的平均$\mathbf{v}^k_{sub}$ 作为Subject传递的信息.
其中$\mathbf{W}^r_{\text{start}}, \mathbf{W}^r_{\text{end}}$ 为关系$r$ 对应的权重参数, $\mathbf{b}^r_{\text {start }}, \mathbf{b}^r_{\text {end }}$ 为关系$r$ 对应的偏置.
接着对如下概率做极大似然:
$$
p_{\phi_{r}}(o \mid s, \mathbf{x})
=\prod_{t \in\{\text { start_o, end_o }\}} \prod_{i=1}^{L}\left(p_{i}^{t}\right)^{\mathbf{I}\left\{y_{i}^{t}=1\right\}}\left(1-p_{i}^{t}\right) ^\mathbf{\mathbf { I } \{ y _ { i } ^ { t } = 0 \}}
$$
$y_i^{\text {start_o }}, y_i^{\text {end_o }}$ 分别为Object的起始结束位置二值化的Tag. $\phi_r$ 为关系特化的Object Tagger的参数.
对于”Null” Object $o_{\varnothing}$, 所有的$y_i^{start\_o_{\varnothing}}, y_i^{end\_o_{\varnothing}}$ 全部为0.
Relation - specific Object Taggers如下图所示:
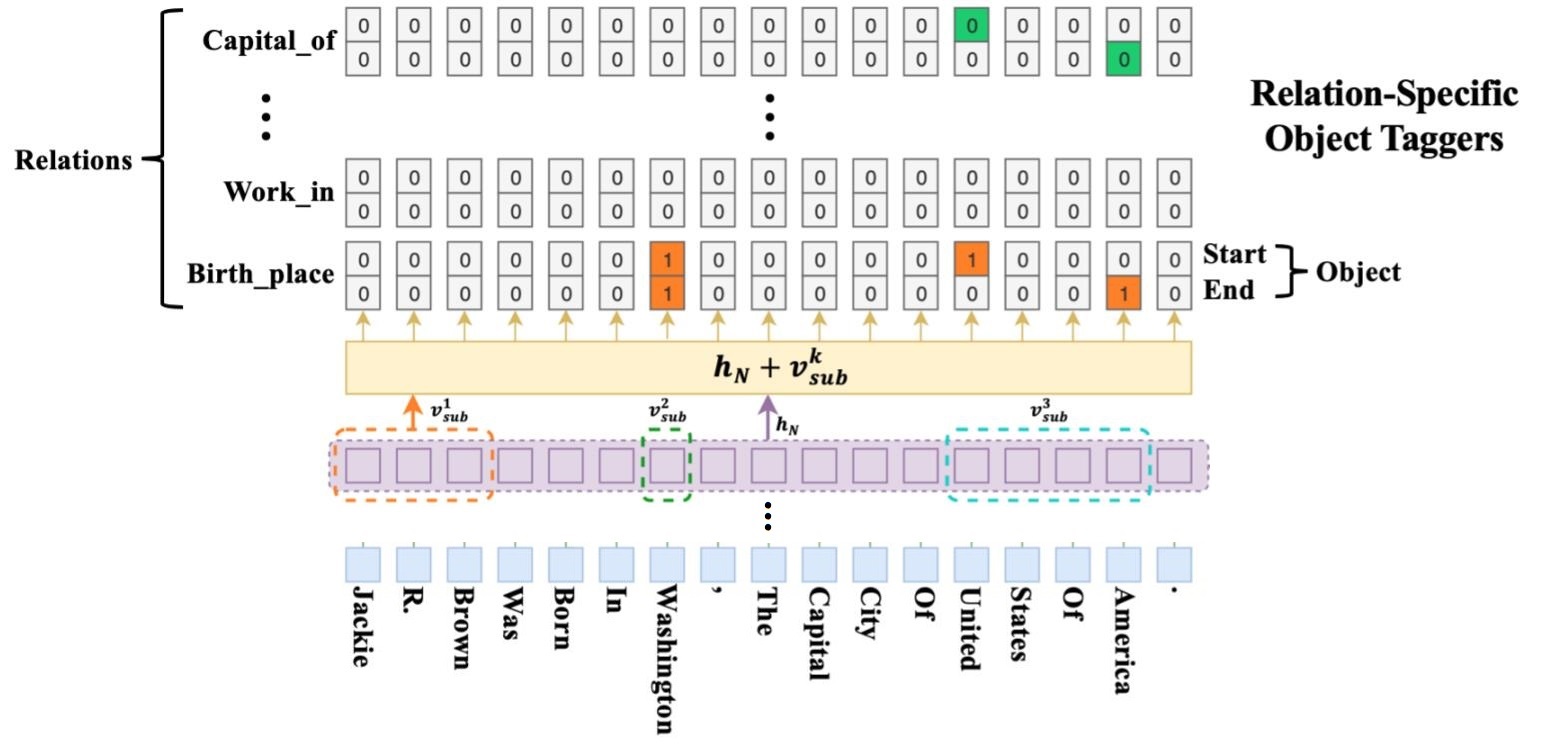
CasRel会在不同的Subject之间迭代. 从Subject Tagger获取了指定的实体后, 简单的将第$k$ 个实体所在区域的Token取平均得到$\mathbf{v}^k_{sub}$, 与BERT抽取出的$\mathbf{h}_N$ 相加, 以此判断句子中所有位置是否有可能含有给定关系$r$ 的Object, 并用起始位置和结束位置来标识Object.
在图中, 假设此时$k=1$, 所选定的Subject为Jackle R. Brown 其可能的关系Birth_place中, 探测到的Object是 Washington 和United States Of America. 故抽取出三元组(Jackle R. Brown, Birth_place, Washington) 及(Jackle R. Brown, Birth_place, United States Of America).
当$k=2$ 时, 绿色的Subject Washington 可能的关系Capital_of中, 探测到的Object为 United States Of America, 图中绿色的位置将会从0变为1, 以此抽取到三元组(Washington, Capital_of, United States Of America).
Data Log-likelihood Objective
根据最前面的推导, 目标函数$J(\Theta)$ 为:
$$
J(\Theta) = \sum_{j=1}^{|D|}\left[\sum_{s \in T_{j}} \log p_{\theta}\left(s \mid \mathbf{x}_{j}\right)+\sum_{r \in T_{j} \mid s} \log p_{\phi_{r}}\left(o \mid s, \mathbf{x}_{j}\right)+\sum_{r \in R \backslash T_{j} \mid s} \log p_{\phi_{r}}\left(o_{\varnothing} \mid s, \mathbf{x}_{j}\right)\right]
$$
使用极大似然优化即可.
总览图如下:

因为对于每种关系都分别检测相应的Object, 感觉就像是一堆指针堆叠起来, 所以也被称为层叠式指针标注.
Experiments
详细的实验参数请参照原论文.
注: 接下来的实验中BERT是没有经过预训练的, 这展示了CasRel强大的潜力.
作者在NYL和WebNLG这两个数据集上做了实验, 数据集的详细信息如下:
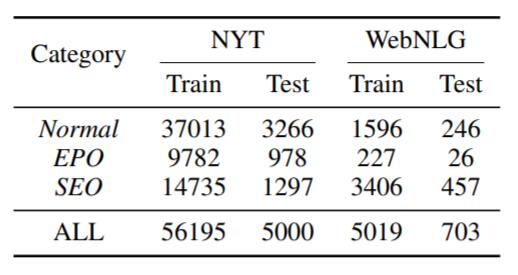
其中NYT规模较大, WebNLG规模较小. 它们都包含有大量的EPO和SEO三元组.
Main Results
在这两个数据集上的结果如下:
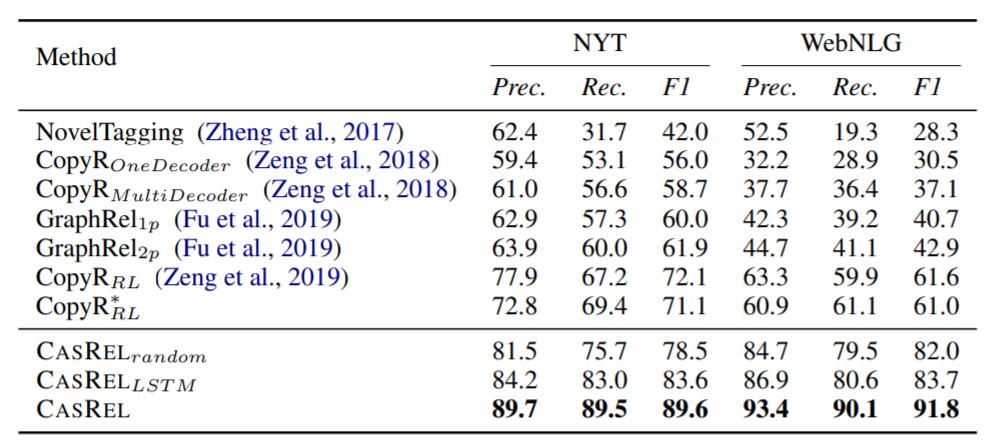
无论是Tagging类的方法, 还是基于图的方法, 基于Copy生成式的方法, 都比CasRel差一大截. 尤其是在重叠三元组很多的WebNLG上, CasRel展示出强大的性能.
Detail Results
面对不同类型的三元组, 各个Baseline在NYT, WebNLG的F1结果如下:
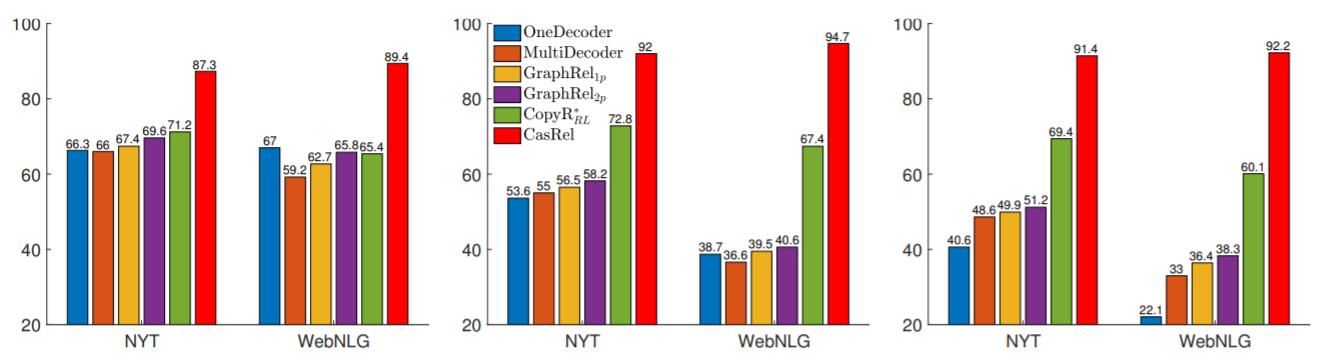
左, 中, 右分别为Normal Class, EPO Class, SEO Class的F1. CasRel在面对重叠三元组时, 比Baseline领先的更多. 这证明了CasRel能较好的解决SEO和EPO问题.
作者还测试了句子中三元组个数不同时, 模型预测它们时的F1, 结果如下:
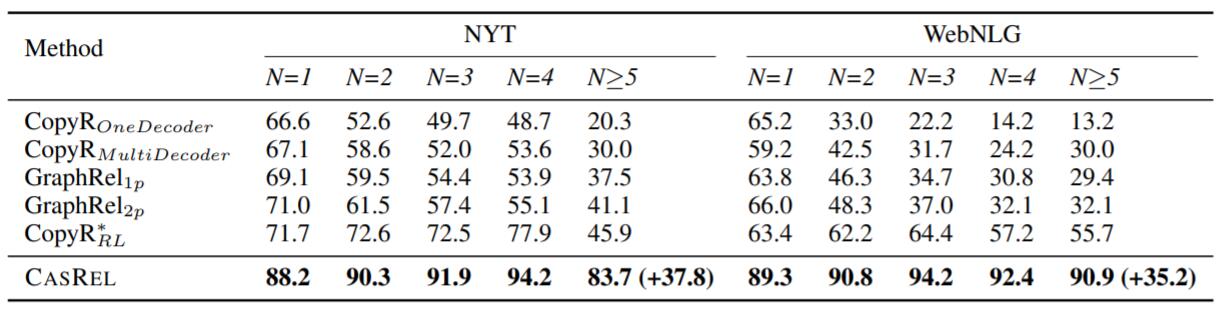
即使是面对句子中5个以上的三元组, 相较于Baseline, CasRel仍然能保证不受过大的影响, 这表明它有更强的鲁棒性和抽取多三元组的能力.
Summary
在本文中, 作者将目光聚焦到三元组重叠问题上, 并提出将关系视为句间实体的映射的思想, 并通过层叠式指针标注的方法, 巧妙的解决了三元组重叠问题.
这是一篇非常有开创性意义的文章, 模型效果相较于之前的Baseline有巨大涨幅.
更为细致的考量, 可以在苏神的文章基于DGCNN和概率图的轻量级信息抽取模型中看到, CasRel仅仅只是把文中的DGCNN换成了BERT, 阅读起来应该不会有问题.

