本文前置知识:
- Depthwise Convolution: 详见深度可分离卷积与分组卷积.
- Attention: 详见Seq2Seq和Attention.
- Transformer: 详见Transformer精讲.
本文是论文PAY LESS ATTENTION WITH LIGHTWEIGHT AND DYNAMIC CONVOLUTIONS的阅读笔记和个人理解. 因为本文的图片均来自于原论文或Reference中的文章, 我觉得列出的几篇文章都很好, 图片特别有助于讲解. 论文中还有大量我不了解的知识, 再有相关的东西再进行补充.
Basic Idea
Self - Attention虽然解决了长距离依赖问题, 但因为计算量大, 必须对文本长度进行限制. 牵扯到计算效率的问题, 自然而然的就想到高效而体积小的卷积. 作者希望用轻量级卷积实现类似Self - Attention的效果.

左侧为Self - Attention的权重生成方式, 右侧为Dynamic Convolution的权重生成方式.
作者希望能通过仅通过每个时刻的输入就能生成注意力权重, 而非像Self - Attention一样依赖全局输入生成.
Depthwise Convolution and Convolution 1D
Lightweight Convolution的核心是单个维度上的深度卷积(Depthwise Convolution).
Convolution in 1 Dimension
无论在多少Dimension的卷积中, Channel维对应的是输入数据相独立的”厚度“这个维度, 它必须能保留输入单元的原始信息, 以保证不同输入元素之间的交互.
例如Conv2d在CV中, 为了保留二维图片的平面位置信息, Channel维对应的是Depth维, 而Conv1d在NLP中, 为了保留一维序列的先后顺序信息, Channel维所对应的是词向量的Hidden维. 这里先入为主,
我开始是Channel维没找对, 卡了很长时间, 希望大家在看的时候从这个角度先入为主.
Depthwise Convolution
深度卷积是一种对每个Channel分别卷积的卷积方式:
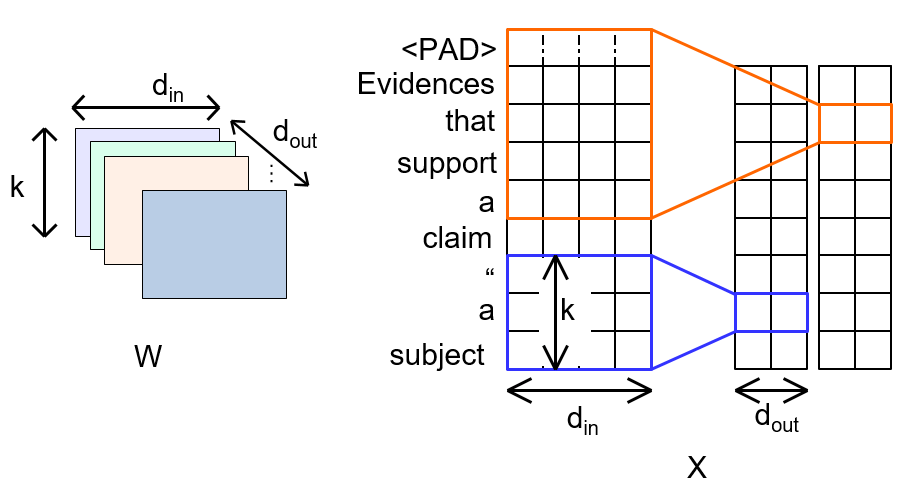
假设你已经具备了深度卷积的基础, 其数学表达如下:
$$
O_{i, c}=\operatorname{DepthwiseConv}\left(X, W_{c,:}, i, c\right)=\sum_{j=1}^{k} W_{c, j} \cdot X_{\left(i+j-\left\lceil\frac{k+1}{2}\right\rceil\right), c}
$$
其中$c$ 代表Channel, $k$ 为卷积核宽度, $i$ 为特征图中Token的位置. 那么$W_{c, :}$ 就代表指定Channel $c$ 的卷积核权重.
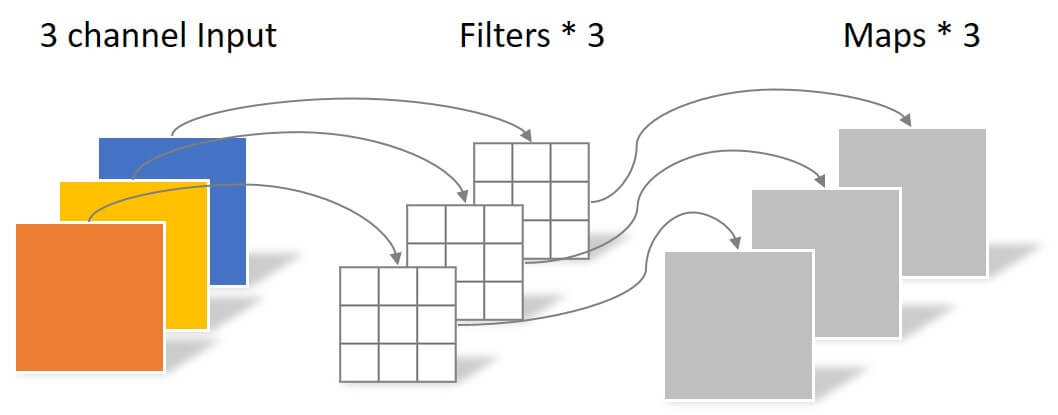
现在我们对已经嵌入好的序列输入做卷积. 如果我们使用的是标准卷积, 那么每次卷积的部分都必须贯穿Channel维, 即对每个Channel使用不同的参数:
因为不同Channel上不共享相同的权重, 所以此时卷积核的参数量为$d_{in} \cdot d_{out} \cdot k$.
如果使用深度卷积, 那么每次卷积就只在每个Channel上单独进行:
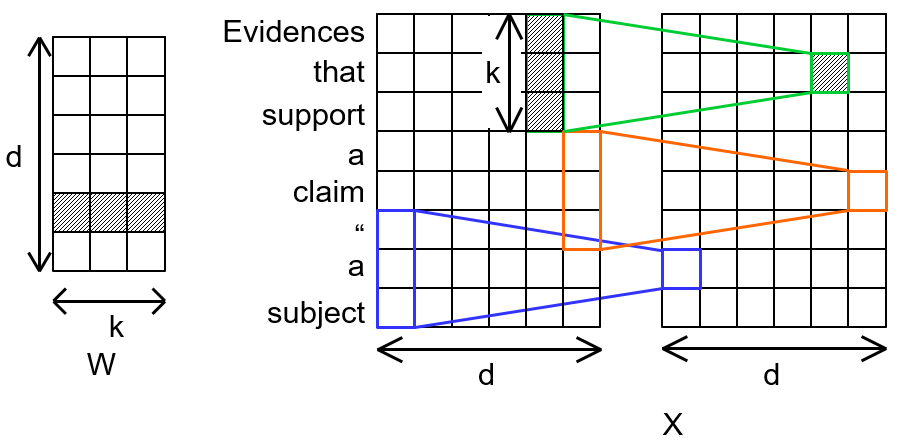
如果$d_{in} = d_{out}=d$, 即维持卷积前后的Channel数不变, 这样参数一下就从$d^2k$ 降到了$dk$, 因为我们不用再做贯穿整个Channel的运算了.
如果我们拿深度卷积的式子举个例子, 当$i=2, c=5, k=3$ 时(即图中所对应的绿色卷积过程), 那么在特征图上第2行第5列的输出$O_{2, 5}$ 则为$O_{2, 5} =W_{5, 1:3}X_{1:3, 5}$.
我开始不能理解为什么参数能下降$d$ 倍, 后来发现我一直都忽视了”代替Self - Attention“这个目的, 在Self - Attention前后, Channel是不变的, 即$d_{in}=d_{out}$. 因此作者说法无误.
Lightweight Convolution
轻量级卷积在深度卷积的基础上进一步改进, 它引入了多头共享权重机制, 使得参数进一步减少.
Weight sharing
为了进一步减少参数量, 作者将Channel维拆成$H$ 个头, 在同一个头覆盖的区域内仅使用一个头(或者说在同一个头内的每个Channel维上的卷积核参数相同):
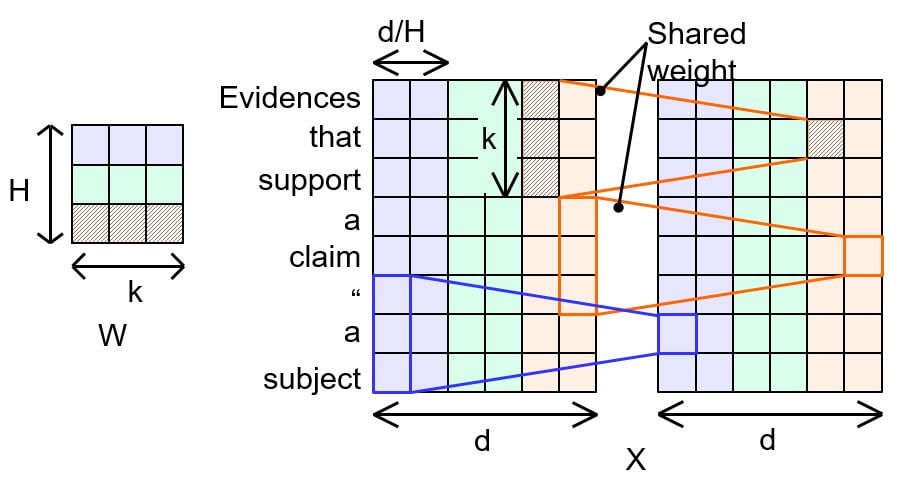
例如上图中, 橙色区域的两个Channel共享同一个卷积核.
经过权重共享, 每个头所占有的Channel数为$\frac{d}{H}$, 这样参数量就缩小为了原来的$\frac{d}{H}$ 倍. 若有$H$ 个头, 参数量进一步从$d \cdot k$ 缩减到$H \cdot k$.
轻量级卷积的数学表达如下:
$$
\operatorname{LightConv}\left(X, W_{\lceil\frac{c H}{d}\rceil,:}, i, c\right)=\operatorname{ DepthwiseConv }\left(X, \operatorname{softmax}\left(W_{\lceil\frac{c H}{d}\rceil,:}\right), i, c\right)
$$
其中$\lceil\frac{c H}{d}\rceil$ 指的是$c$ 属于哪个头, $\frac{c}{d}$ 指的是Channel $c$ 在Channel维总深度$d$ 中所处的位置百分比. 因为一共就有$H$ 个头, 所以每个头占总Channel的$\frac{1}{H}$. 那么$\lceil\frac{c}{d} \div \frac{1}{H}\rceil$ 就能算出$c$ 的位置前面到底有几个头, 向上取整就是$c$ 所属的头位置.
输入时对卷积核Softmax归一化详见下一小节.
Softmax Normalization
我们最初的目标是通过卷积来代替自注意力机制, 所以仅仅通过卷积得到还不足够, 我们必须将其归一化形成权重, 才能够符合注意力权重的标准. 由于权重是对不同时间步分配的, 所以在卷积核大小$k$ 对卷积核内部进行权重归一化:
$$
\operatorname{softmax}(W)_{h, j}=\frac{\exp W_{h, j}}{\sum_{j^{\prime}=1}^{k} \exp W_{h, j^{\prime}}}
$$
其中$W \in \mathbb{R}^{H \times k}$, 为多头卷积核的权重矩阵. 通过Softmax归一化, 同一个卷积核中的参数只能得到固定的注意力权重, 因为我们目前仅仅是对卷积核权重这个固定参数上归一化, 而没有结合当前时刻的输入信息.
Gated Linear Units
GLU是一种应用在CNN上的一种门控机制, 于Language Modeling with Gated Convolutional Networks中提出, 该结构能够提升CNN抽取高层抽象特征的能力, 其核心思想如下:
$$
h_{l}(\mathbf{X})=(\mathbf{X} \ast \mathbf{W}+\mathbf{b}) \otimes \sigma(\mathbf{X} \ast \mathbf{V}+\mathbf{c})
$$
其中$\ast$ 代表卷积操作, $\mathbf{X}$ 代表输入矩阵, $\mathbf{W}, \mathbf{V}$ 代表两卷积核, $\mathbf{b}, \mathbf{c}$ 代表两卷积偏置, $\otimes$ 代表逐元素点乘.
在GLU中, 最基本的Block被定义为:
$$
\operatorname{GLU}(X) = X + \operatorname{CNN}(X) \otimes \operatorname{CNN}(X)
$$
残差连接和门控CNN就组成了最小的GLU单元.
Module
轻量级卷积模块由Linear, GLU, LConv, Linear依次组成. 第一个Linear先将Token的Embedding维度从$d$ 投影映射到$2d$, 接着通过一个门控来调控输入的信息量, 再通过轻量级卷积, 最后再接一个Linear将维度调整回$d$:
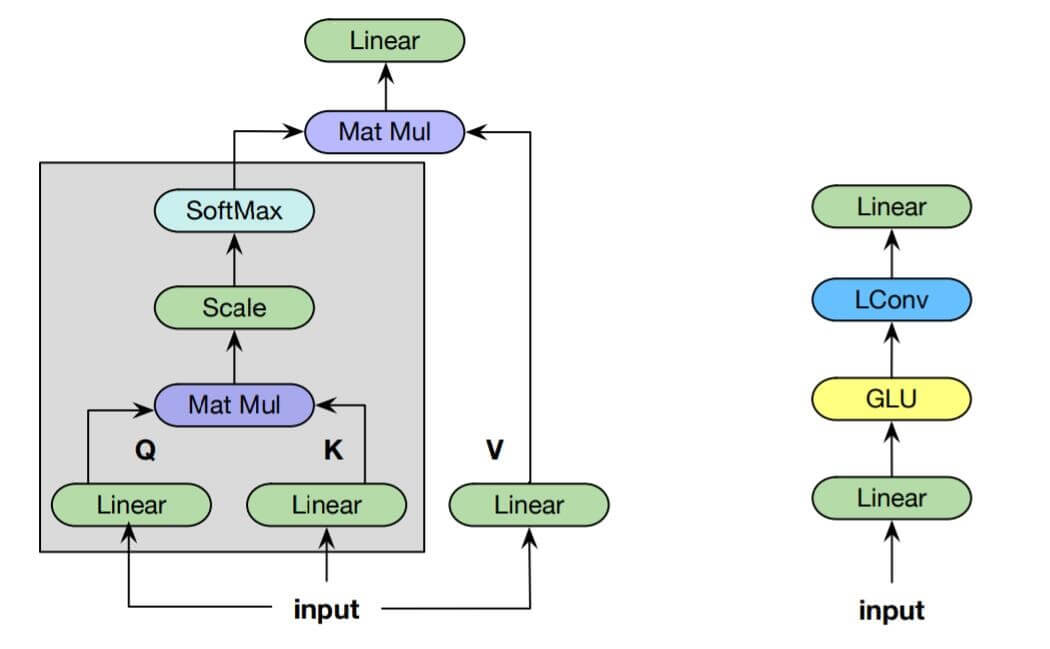
左图为Transformer中使用的点击缩放注意力, 右图为作者目前提出的轻量级卷积模块, 输入维度和输出维度是一致的.
Dynamic Convolution
目前的轻量级卷积在不同时间步的权重都是固定的, 根本没有达到动态生成权重的效果, 基于轻量级卷积, 作者进一步提出动态卷积, 动态卷积对每个位置的权重都是动态的.
$$
\begin{aligned}
\operatorname{DynamicConv}(X, i, c)&=\operatorname{LightConv}\left(X, f(X_{i})_{h,:}, i, c\right) \\
&=\operatorname{ DepthwiseConv }\left(X, \operatorname{softmax}\left(f(X_{i})_{h,:}\right), i, c\right)
\end{aligned}
$$
其中$f$ 是一个简单的可学习的线性变换$W^Q$, 例如$f(X_{i})=\sum_{c=1}^{d} W_{h, j, c}^{Q} X_{i, c}$. 它能将当前时刻的$d$ 维的输入转化成$H\times k$ 维的注意力权重.
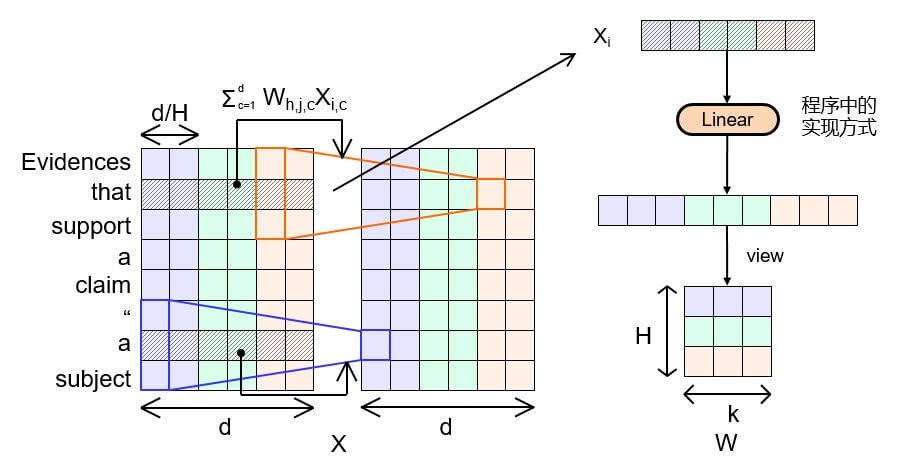
简而言之, 就是利用某个时刻(实际上是Token)的全部Channel信息为当前时刻窗口内所有头的卷积核参数赋予权重, 而当前时刻Token的内容就相当于Self - Attention中的Query.
注意力权重的生成只取决于当前时刻的输入, 而与前时刻和后时刻输入无关, 这是一个严重缺陷.
下图依次为点积缩放注意力, 轻量级卷积模块, 动态卷积模块.
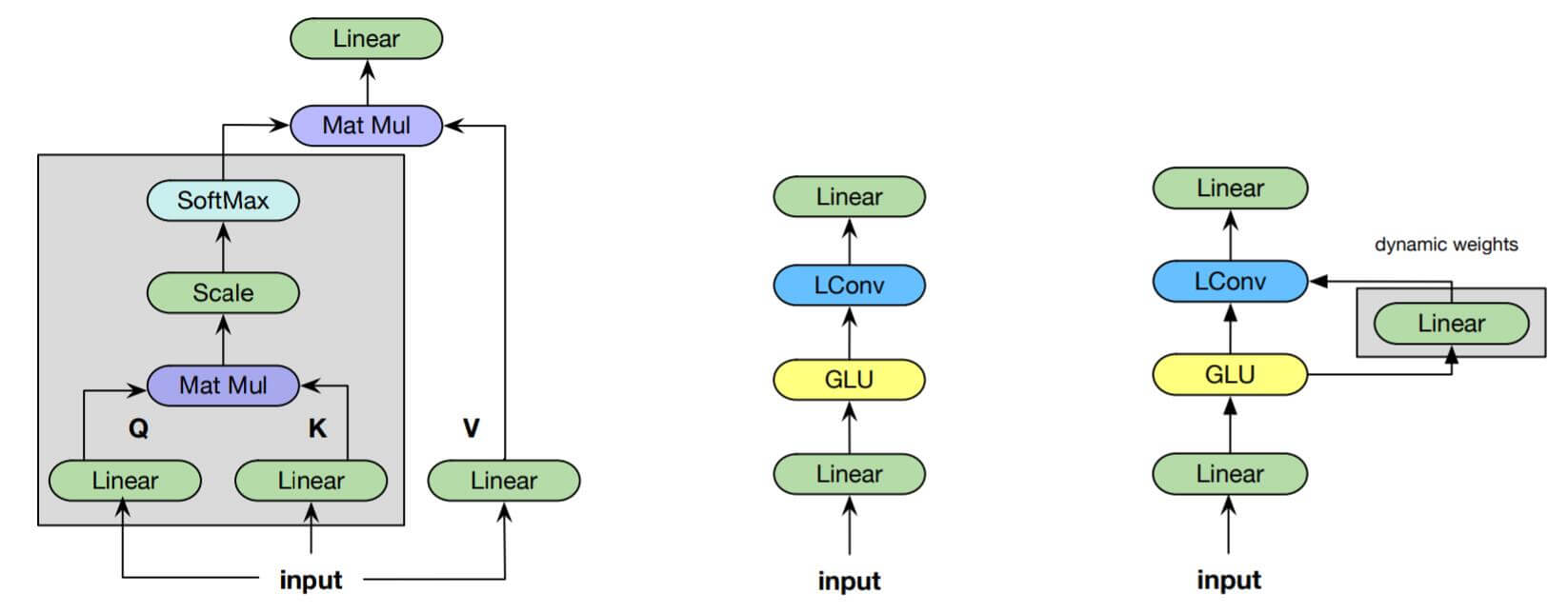
动态卷积模块与轻量级卷积相比, 只是多增加了一个动态分配权重的Linear层.
Experiments
作者在机器翻译, 语言建模, 文本摘要任务上将Transformer中的自注意力机制换成轻量级卷积或动态卷积测试本方法的性能. 在Encoder中, 将自注意力模块替换, 在Decoder中将Masked自注意力模块替换.
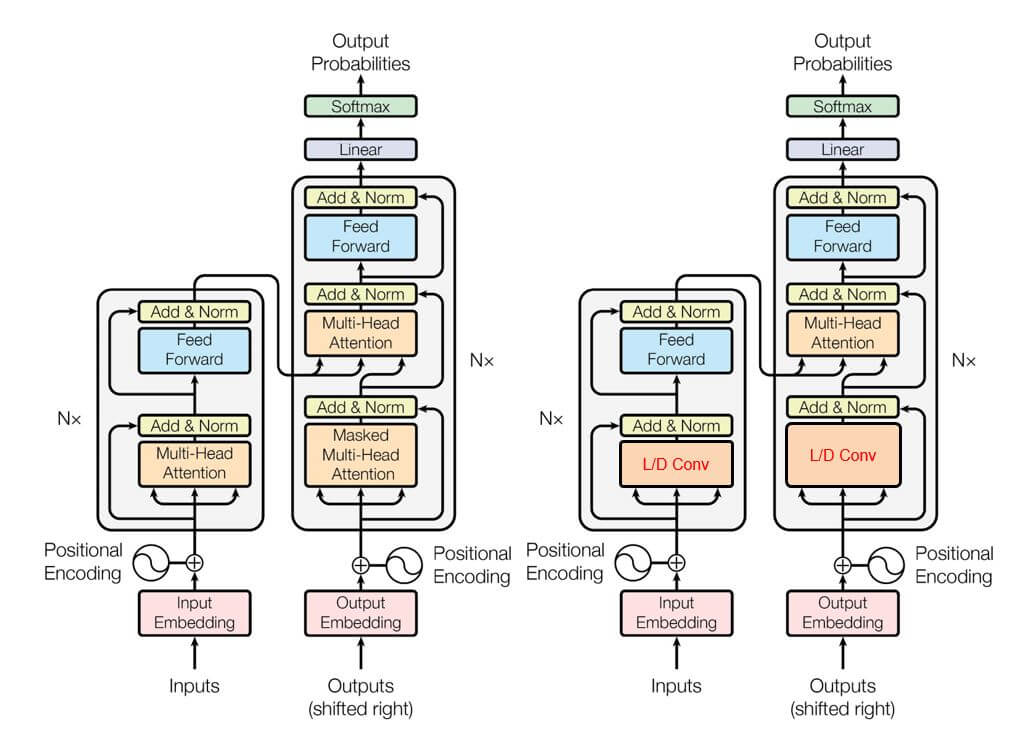
针对具体任务作者进行了不同的调整, 详细配置请参照原论文.
作者提出, 参数量近似的情况下对比性能. 所以并没有采用6层的Block堆叠, 而是使用了7层. 这七层中, 卷积核大小依次为3, 7, 15, 31, 31, 31, 31.
高层卷积核窗口设置的比较大, 我猜还是因为高层特征抽取中卷积的局部性限制问题. 在BERT的Attention可视化对高层能观察到, 除了一些特定层能很明显的体现出注意力差异, 其他高层基本上是均摊注意力权重, 所以卷积核需要更大范围的捕捉上下文特征相关性.
Machine Translation
作者分别在newstest2014上测试了BLEU准确率:
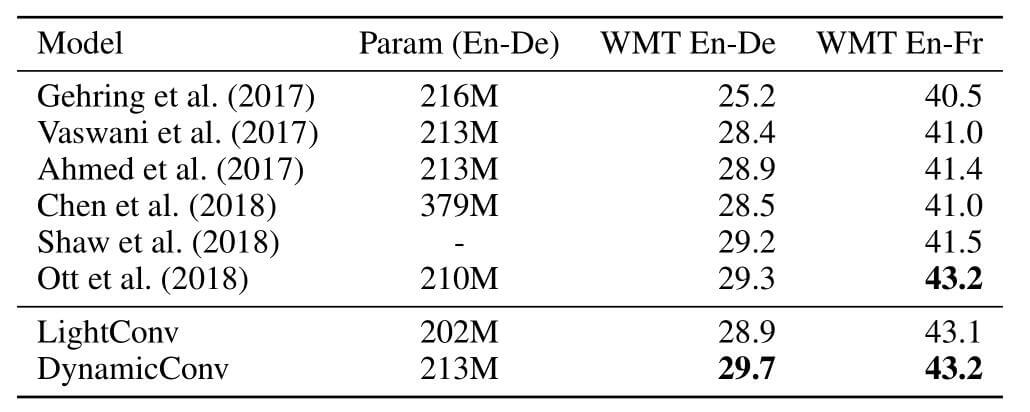
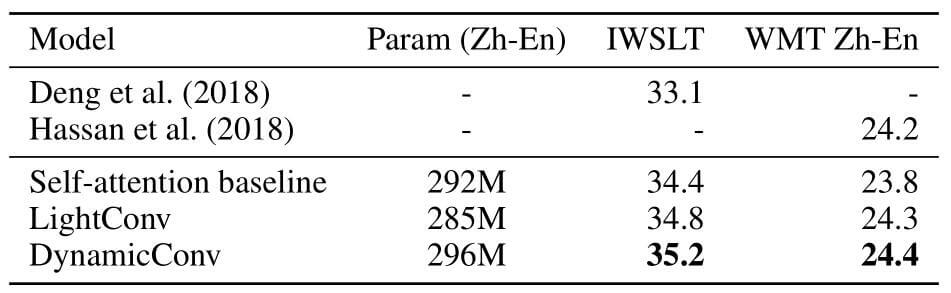
动态卷积与原生Transformer在参数量相同的情况下有较大提升.
Model Ablation
消融实验结果如下:
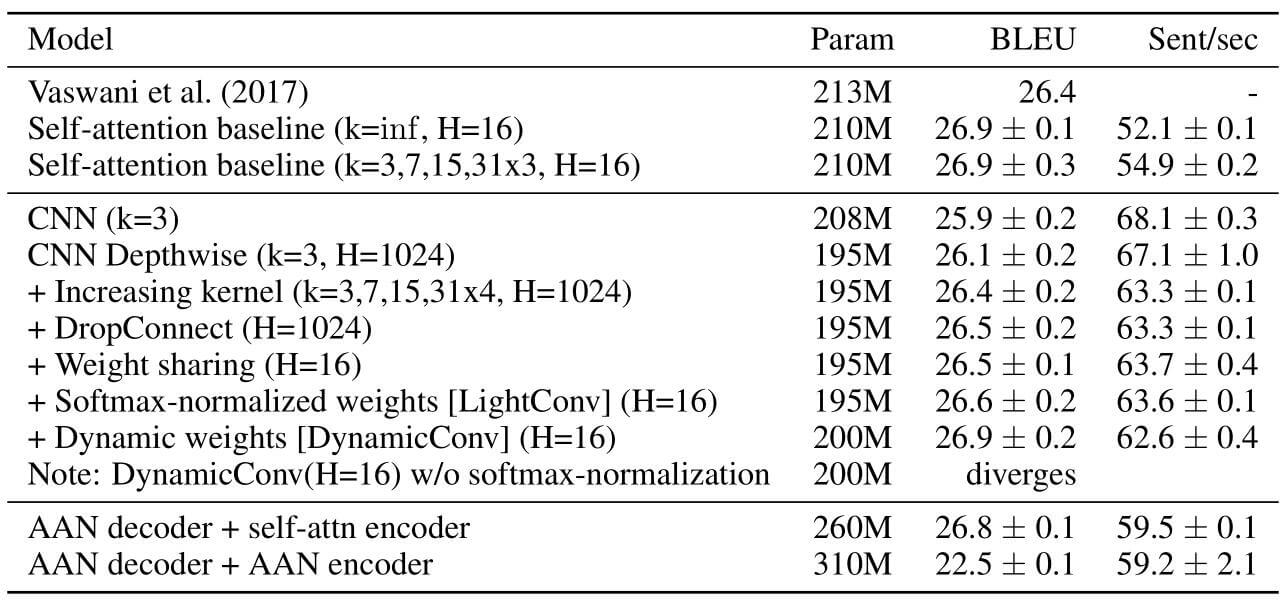
感觉小Trick颇多, 权重共享在提高句子推断速度上有较大贡献. 在性能提升上每种Trick的贡献都差不多.
Language Modeling
在Google Billion Word上以困惑度为指标结果如下:

动态卷积的参数比自注意力还稍多, 在测试集上取得了略胜自注意力一丢丢的成绩…
Abstractive Summarization
作者在CNN - DailyMail中的文本摘要实验结果:
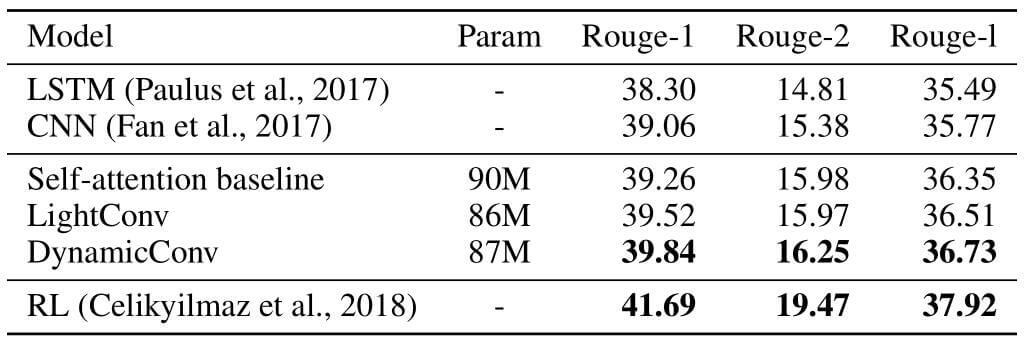
轻量级卷积略胜一筹, 但其实也还是没节省多少参数.
从实验结果来看, 轻量级卷积在相同参数的情况下给出了一定的性能提升, 但并没有比较更少参数和其他模型的对比. 此外, 实验中的结果跟具体任务下的参数微调绝对是分不开的.

