2020.09.25: 本质部分的猜想被证实.
2020.09.21: 更新Attention的本质.
2020.09.19: 在接触了更多NLP内容后, 发现Attention是一个有特殊表征意义的结构, 以后会加入更深的理解.
Seq2Seq和Attention
Seq2Seq和Attention被广泛的应用于RNN中, 当然现在不单单只是在NLP中使用, CV领域也有很多应用.
RNN回顾
在之前的循环神经网络小结中对RNN进行了介绍. 在此简单回顾一下.
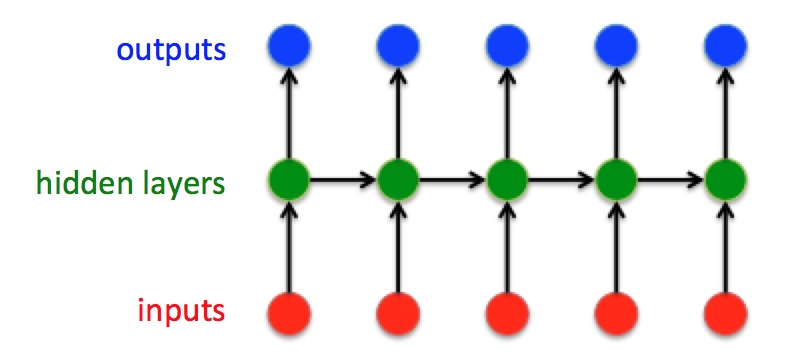
RNN是针对时序序列数据而诞生的神经网络, 其输入是时序数据, 每个时刻$t$ 都会有一个相应的输出和隐藏状态. 对于$t \in T$, 有输入$[x_{1}, x_{2}, \ldots, x_{t}, \ldots, x_{T}]$ 和输出$[y_{1}, y_{2}, \ldots, y_{t}, \ldots, y_{T}]$ . 在经典RNN结构中给出的输入和输出是相同大小的.
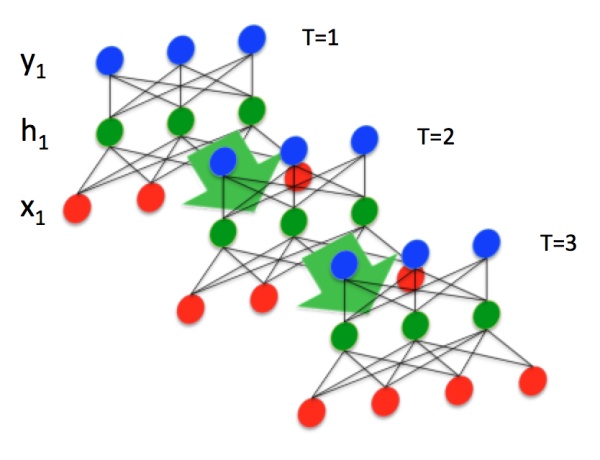
当前时刻隐藏状态$h_t$ 随着下个时刻$t+1$ 的输出$x_{t+1}$一起被共同作为下个时刻的输入.
Sequence to Sequence(Encoder-Decoder)
Seq2Seq作为一种不限制输入和输出的序列长度的结构, 被广泛应用于机器翻译, 文本摘要, 阅读理解, 语音识别等任务中. 在Seq2Seq结构中, 编码器Encoder把所有的输入序列都编码成一个统一的语义向量, 保存在hidden state中, 然后再由解码器Decoder解码. 这种结构其实在介绍RNN结构时提到过. Seq2Seq和Encoder-Decoder描述的是同一种结构.
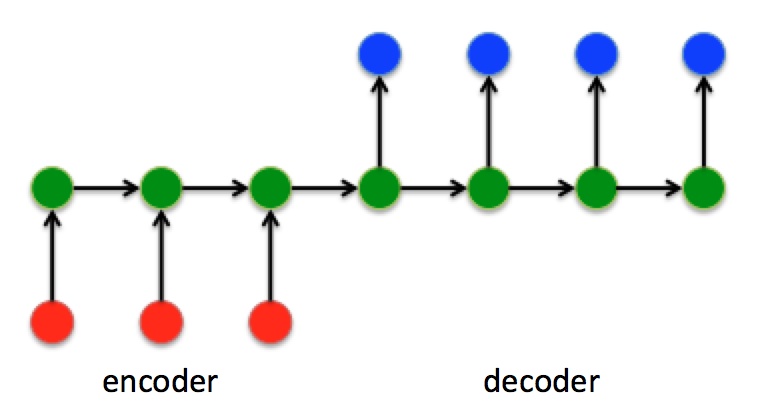
这种结构使得输入和输出与经典的RNN结构不同, 输入和输出的数据维度可以不同. 在解码器Decoder解码的过程中, 反复将上一个时刻$t-1$ 的输出作为当前时刻$t$ 的输入, 循环解码, 直到输出停止字符才停止.
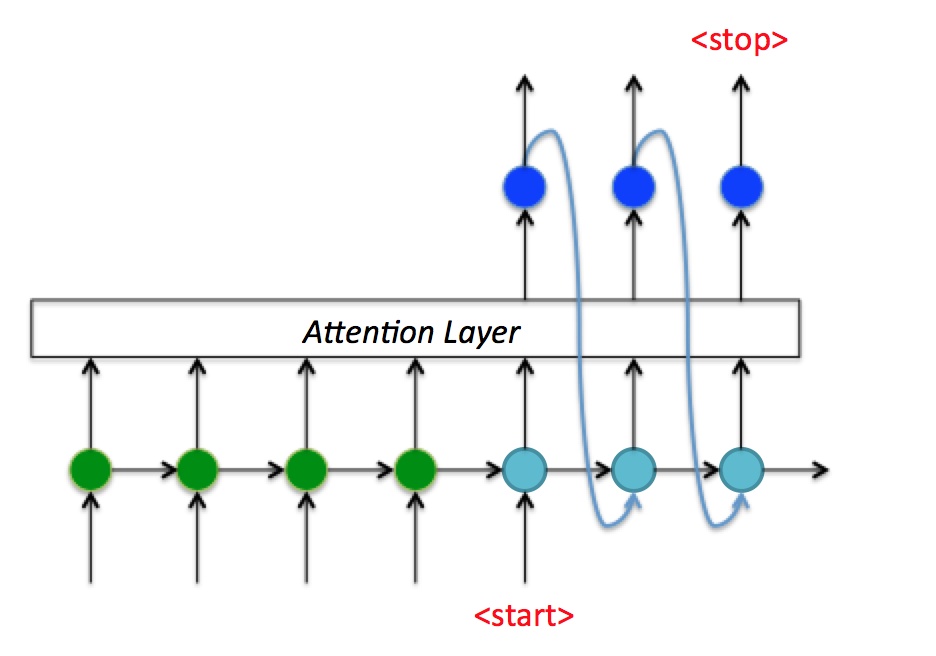
下面以机器翻译为例, 来看一种Seq2Seq结构的一种经典实现方式. 将中文的”早上好”通过seq2seq转换成英文的”Good morning”.
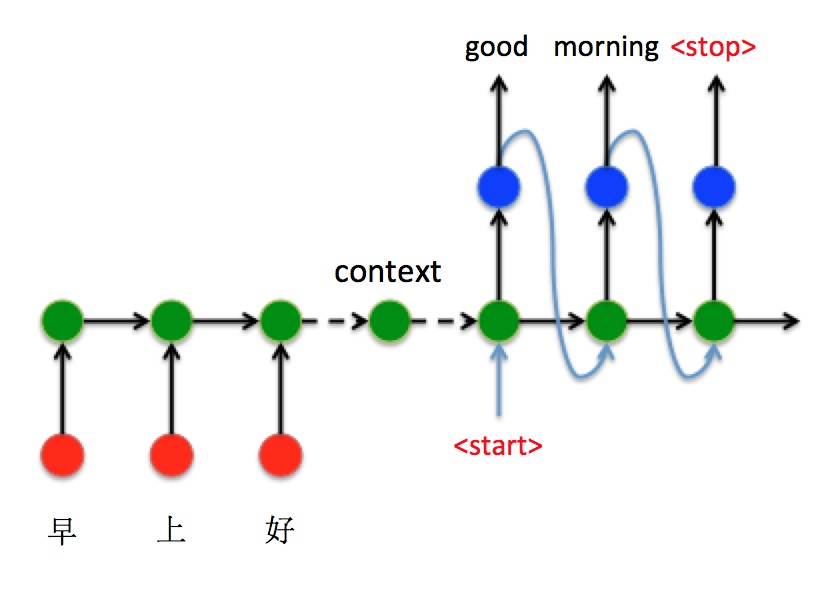
- 将”早上好”通过Encoder编码, 从$t=1$ 时刻到$t=3$ 时刻通过RNN反复完成语义向量的编码, 将$t=3$ 时刻最终的隐藏状态$h_3$ 作为语义向量.
- $h_3$ 作为Decoder的初始隐藏状态$h_0$, 并在$t=1$ 时刻输入标识开始解码的特殊标识符
<start>, 开始解码. 不断的将上一时刻输出作为当前时刻输入进行解码, 最终输出停止字符<stop>时, 预测解码停止.
$t$ 时刻时, Decoder中的数据流流向如下所示:
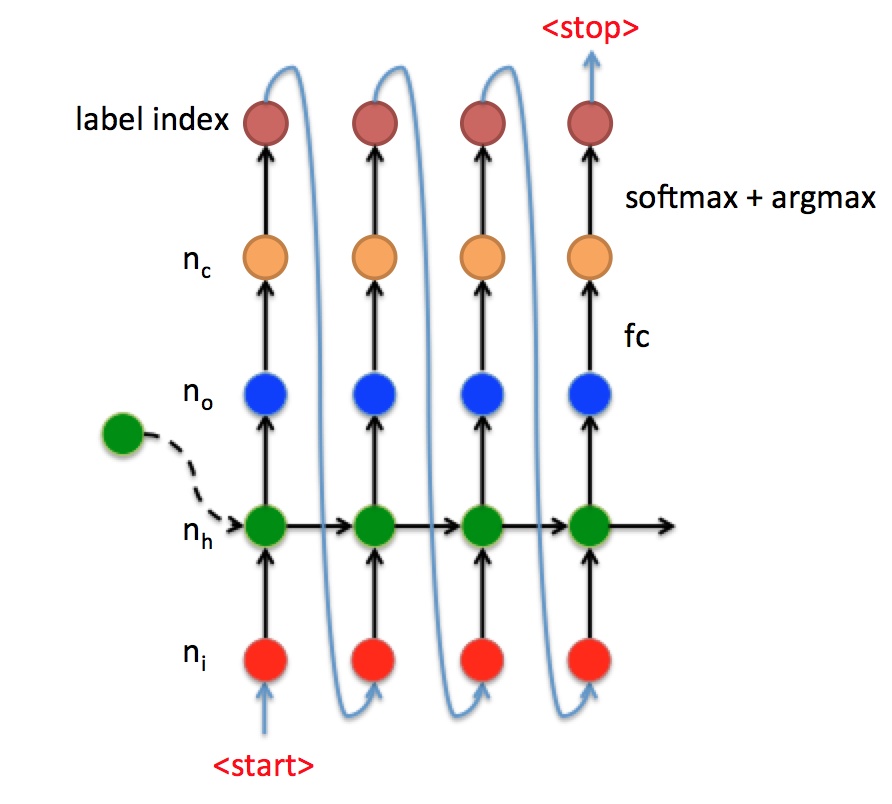
- RNN先被输入大小为$[n_i, 1]$ 的向量$x_t$, 即红点.
- 结合传过来的语义向量, 加上这个时刻的输入, 经过RNN后输出大小为$[n_o, 1]$ 的向量$y_t$, 即蓝点.
- 在获取了输出向量后, 获取输出向量所对应的字符, 这就需要结合一层全连接层和激活函数(主要是Softmax), 将输出向量变为$y_t’$, 大小为$[n_c, 1]$, 即图中的黄点. $n_c$代表字典中的总字符数. 从$y_t’$ 中找到概率最大的字符index, 即图中橘红色点.
- 将分类后获取的字符index做一次Embedding(之前的NLP相关那篇文章中有提到过Word2vec), 输入给下个时刻, 如此循环.
当然也有人将语义向量作为Decoder的输入, 而非隐藏状态提供给Decoder. Seq2Seq只是代表一种结构, 而非某种具体的实现方法.
但是Seq2Seq有许多的缺点:
- 最大的局限性: 编码和解码之间的唯一联系是固定长度的语义向量.
- 编码要把整个序列的信息压缩进一个固定长度的语义向量.
- 语义向量无法完全表达整个序列的信息.
- 先输入的内容携带的信息, 会被后输入的信息稀释掉, 或者被覆盖掉. 信息的量越大, 损失就越大.
- 输入序列越长, 这样的现象越严重, 这样使得在Decoder解码时一开始就没有获得足够的输入序列信息, 解码效果会打折扣.
Attention机制
这里说的Attention都是软注意力机制.
正是为了弥补基础的Encoder-Decoder的局限性, 提出了Attention. 因为语义向量表达信息的缺失性, 遗忘性, 以及向量长度的不可变性, Attention想要利用Encoder的隐藏状态$h_t$ 来解决语义向量存在的弊病. 当然, Attention不单单广泛的应用在NLP领域, 在CV领域也常有应用.
Attention结构
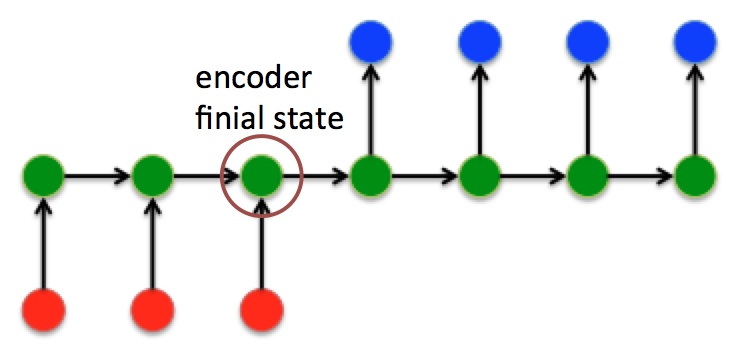
Attention的实质就是在Decoder的输入端, 将Encoder的隐藏状态加权信息, 也作为输入的一部分, 提供给Decoder. 换句话说, Encoder不再传递最后一个时间步的隐藏状态, 而是将所有时间步的隐藏状态加权提供给Decoder.
假设Encoder经过了3个时间步, 对应的隐藏状态分别是$h_1, h_2, h_3$, 分别的输入是”早”, “上”, “好”, 那么Decoder在$t=1$ 时刻通过三个不同的权重$w_{11}, w_{12}, w_{13}$ 能加权计算出一个向量$c_1$.
$$
c_{1}=h_{1} \cdot w_{11}+h_{2} \cdot w_{12}+h_{3} \cdot w_{13}
$$
将$c_1$ 和上一个状态拼接在一起形成一个新的向量, 一起输入到Decoder中, 计算结果:
$$
\bar{h}_{0} \leftarrow \operatorname{concat}\left(\bar{h}_{0}, c_{1}\right)=\operatorname{concat}\left(h_{3}, c_{1}\right)
$$
这样, 在Decoder的$t=1$ 时刻, 就应该根据之前Encoder的隐藏状态加权得到一个新的向量$c_2$, 和Decoder的上一个隐藏状态一起输入得到计算结果:
$$
\begin{array}{c}
c_{2}=h_{1} \cdot w_{21}+h_{2} \cdot w_{22}+h_{3} \cdot w_{23} \\
\bar{h}_{1} \leftarrow \operatorname{concat}\left(\bar{h}_{1}, c_{2}\right)
\end{array}
$$
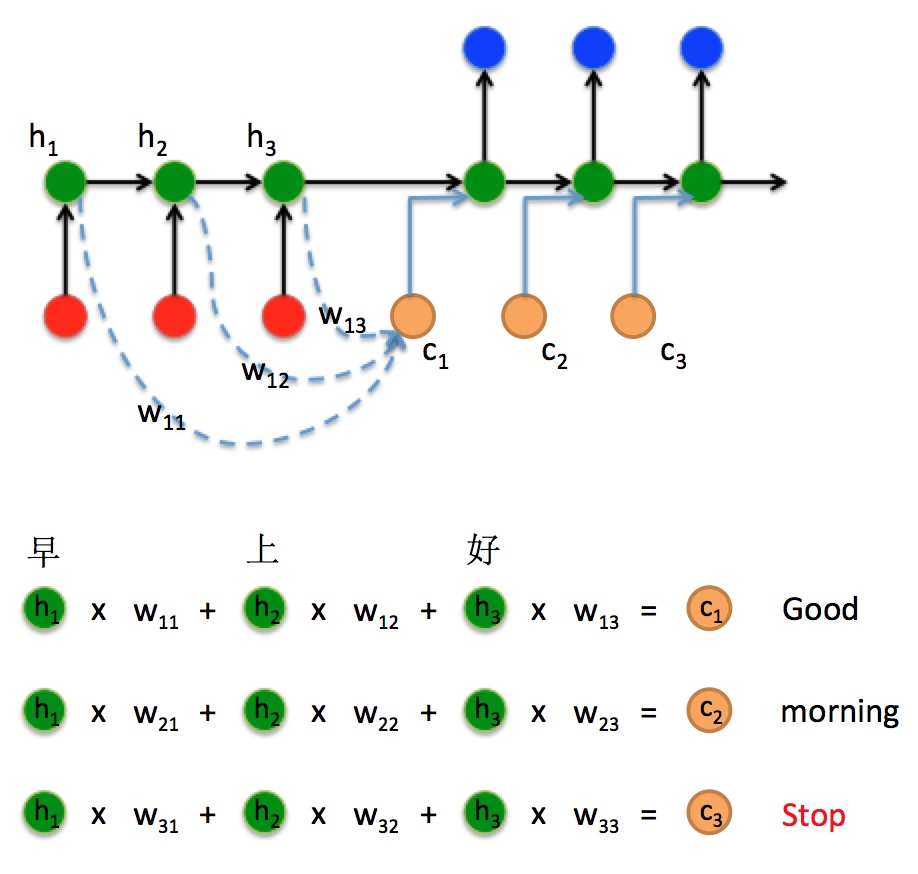
在Decoder的$t=2$ 和$t=3$ 时刻同理, 由于权重不同, 所以Decoder在解码时对隐藏状态关注的部分就不同, 权重越大注意力越强. 比如, 在翻译”好”时, 关注点应该在$h_3$ 上, 所以对应的$w_{13}$ 就应该比$w_{11}$ 和$w_{12}$ 大得多.
如果把隐藏状态和权重视为一层神经层, 那么就可以看做Encoder和Decoder之间引入了一层跨越时间步的神经层.
Attention又有 Bahdanau Attention 和LuongAttention 等多种实现. 这里说一下LuongAttention.
LuongAttention
重新定义符号, 用$\bar{h}_{s}$ 代表Encoder的隐藏状态, $h_t$ 代表Decoder的隐藏状态, $\tilde{h}_{t}$代表Attention Layer输出的最终Decoder状态.
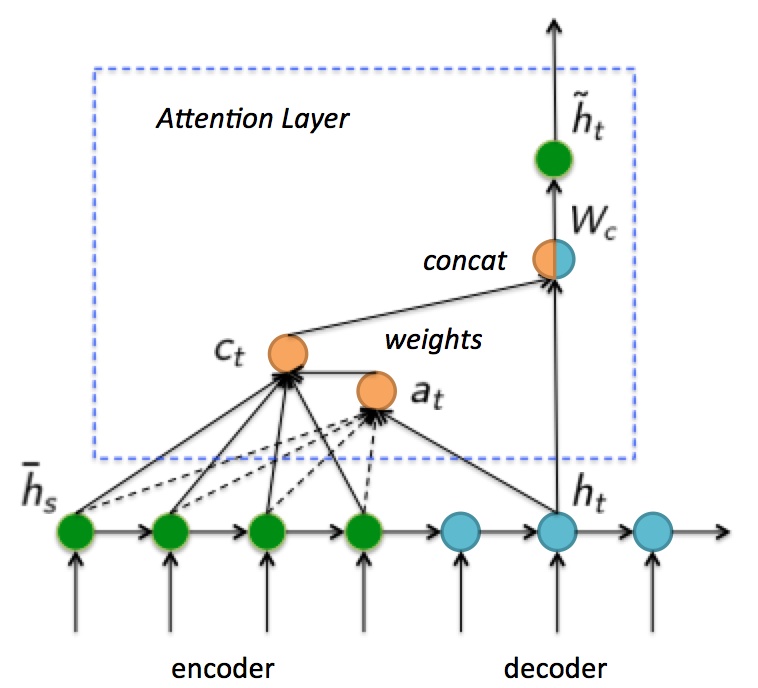
首先要计算权重. 如果Decoder在$t$ 时刻的隐藏状态为$h_t$, Encoder每一个隐藏状态$\bar{h}_{s}$ 的权重为$a_{t}$, 则权重是由规则$\mathrm {score}$ 经过$\mathrm {Softmax}$ 函数后得出的:
$$
a_{t}(s)=\frac{\exp \left(\operatorname{score}\left(h_{t}, \bar{h}_{s}\right)\right)}{\sum_{s^{\prime}} \exp \left(\operatorname{score}\left(h_{t}, \bar{h}_{s^{\prime}}\right)\right)}
$$
在luong Attention中, $\mathrm {score}$ 可以通过多种方式来计算:
$$
\operatorname{score}\left(h_{t}, \bar{h}_{s}\right)=\left\{\begin{array}{ll}
h_{t}^{T} \bar{h}_{s} & \text { Dot } \\
h_{t}^{T} W_{a} \bar{h}_{s} & \text { General } \\
v_{a}^{T} \tanh \left(W_{a} \cdot \operatorname{concat}\left(h_{t}, \bar{h}_{s}\right)\right) & \text { Concat }
\end{array}\right.
$$
$\mathrm {Dot}$ 指的是向量内积, $\mathrm {General}$ 是再通过乘以权重矩阵$W_a$ 进行计算. 一般情况下来说$\mathrm {General}$ 要好于$\mathrm {Dot}$.
然后将计算得来的权重与Encoder的隐藏状态进行加权求和, 生成新的向量$c_t$.
$$
c_{t}=\sum_{s} a_{t}(s) \cdot \bar{h}_{s}
$$
接着将加权后的向量$c_t$ 与原始Decoder的隐藏状态$h_t$ 拼接在一起.
$$
\tilde{h}_{t}=\tanh \left(W_{c} \cdot \operatorname{concat}\left(c_{t}, h_{t}\right)\right)=\tanh \left(W_{c} \cdot\left[c_{t} ; h_{t}\right]\right)
$$
因为是拼接, 所以向量$c_t$ 和$h_t$ 拼接后的大小一定会发生变化. 如果想恢复成原来的形状则需要再乘一个恢复矩阵$W_c$ (也是用来重置大小的全连接层), 当然也可以不恢复, 只是会导致Decoder 的每个Cell大小逐渐变大.
最后, 对引入注意力的Decoder的 $\tilde{h}_{t}$ 经过一次线性运算后得到输出.
$$
y_{t}=W_{h o} \tilde{h}_{t}+b_{h o}
$$
也可以根据需要将新生成的状态$\tilde{h}_{t}$ 送入RNN继续学习. 上述过程提到的矩阵$W_a$, $W_c$, $W_{ho}$ 均通过学习得来.
Attention的真正本质
该部分为Transformer的前置知识.
图和部分内容出自浅谈Attention机制的理解.
虽然在Seq2Seq中, Attention可以看做是跨越时间步的神经层, 但只有抛弃掉开始接触的RNN和Seq2Seq, 才能看到Attention本身, 目前我们对Attention的理解是基于RNN和Seq2Seq的, 对这两种结构做了捆绑后并不能很好的看清它. 在抛弃了Seq2Seq后, 我们仍然说Attention的本质是对某些数据分配某些权重参数, 然后再对它们进行合并.
比较广泛的一个说法是, Attention的本质是一个查询(Query)到一系列键值对(<Key - Value>)的映射. 有些人将它比作软寻址的过程, 也是一样的道理, 当有Query = key的查询时, 根据内容的重要性, 从每个Value中都取出所需要的内容, 再通过某种方式合成起来形成输出.
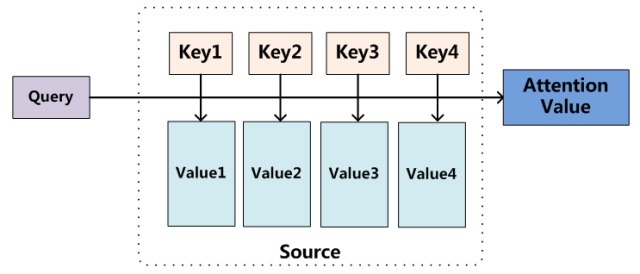
假设Key和Value是不同语言中一一对应的单词, 如果根据Key能够产生一个与Value有关的概率分布, 不难发现, 这个过程和传统机器翻译中做的短语对齐起到的功能是类似的.
如果在目标中进行某数据的查找, 对于一个Query, 通过计算Query与所有Key之间的相似度或相关性, 再通过归一化得到与Value对应的概率分布(权重), 将其与对应的Value加权求和就得到了输出.
如果Key = Value 则被称为普通模式, Key != Value 被称为键值对模式. 目前在大多数NLP研究中, Key和Value是相同的.
这个结论我看很多人提到过, 我表示不理解, 想了很久目前也只有一个猜测, 我个人认为与应用领域有关.
重点在于, 之所以有Key-Value的映射结构, 很有可能在某些领域中Key的信息和对应的Value信息不是完全相同的, 这就意味着Key只用来生成权重系数, 而Value作为与Key不相同的语义信息可能有其他含义.
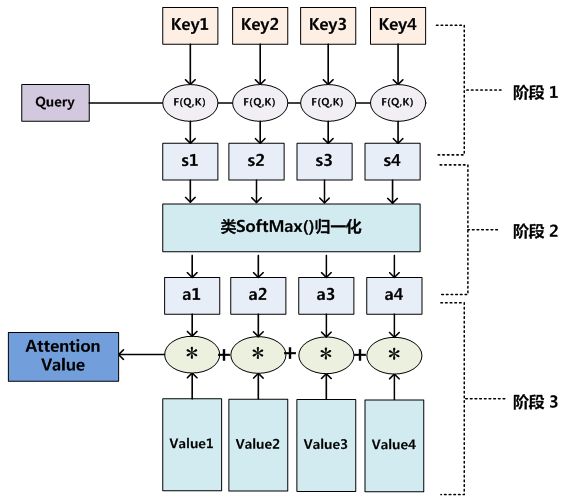
可能上面写的比较散, 做个小总结, 工作机制有三步:
- 计算Query与Key的相似度, 得到权值, 常用的相似度函数有点积,拼接,感知机等, 当然也可以不是相似度, 是其他的打分函数.
- 对权值进行各种Softmax归一化.
- 用归一化得来的权值与Value加权求和.
因此, 有Attention:
$$
\begin{aligned}
& \alpha _i = \operatorname {softmax}(\operatorname {similarity}(QK^T)) \\
& attention((K, V), Q) = \sum_{i=1}^N \alpha_i v_i \quad(v_i \in V)
\end{aligned}
$$
注: 该公式在Transformer中还会再次出现.
如果把<Key - Value>这个映射称为字典, 那么Attention能够根据之前形成的字典轻松捕捉局部和长期依赖. 另外, Attention也可以看做是一种基于全连接的图模型, 只是连接权重是动态生成的.

总结
下面来总结一下, 图片出自Visualizing A Neural Machine Translation Model.
在Encoder如何获取经过Attention加权后的向量:
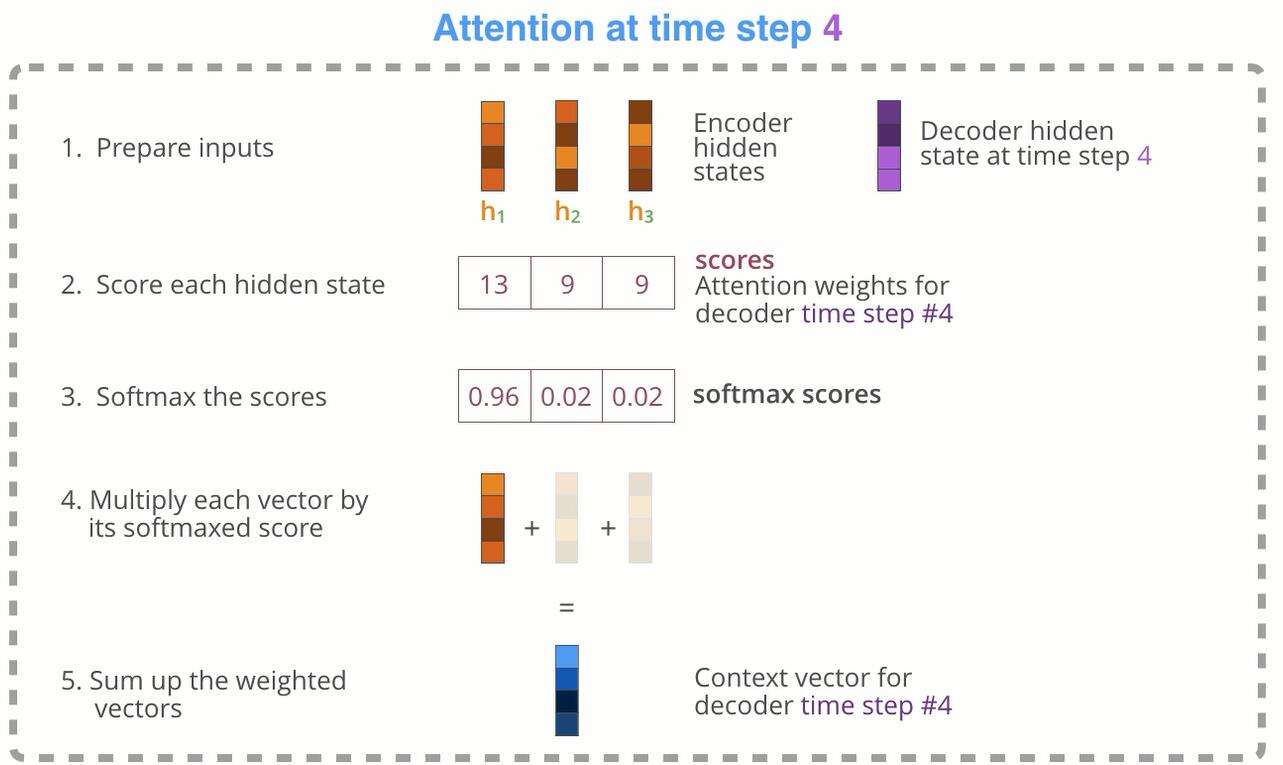
从Decoder得到输出的计算过程:
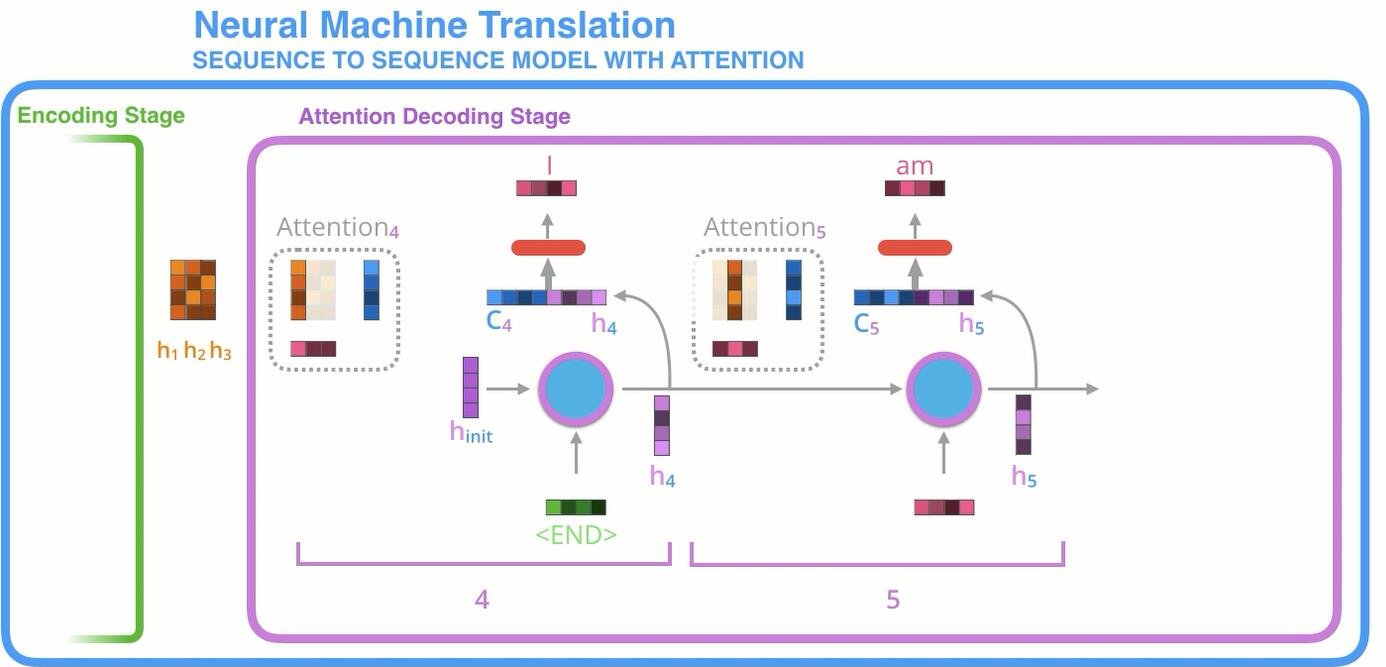
优缺点分析
Attention优点:
- 在机器翻译时, 让生词不只是关注全局的语义向量, 增加了”注意力范围“. 表示接下来输出的词要重点关注输入序列种的哪些部分. 根据关注的区域来产生下一个输出.
- 不要求Encoder将所有信息全输入在一个固定长度的向量中.
- 将输入编码成一个向量的序列, 解码时, 每一步选择性的从序列中挑一个子集进行处理.
- 在每一个输出时, 能够充分利用输入携带的信息, 每个语义向量不一样, 注意力焦点不一样.
Attention缺点:
- 需要为每个输入输出组合分别计算Attention, 50个单词的输出输出序列需要计算2500个attention.
- attention在决定专注于某个方面之前, 需要遍历一遍记忆再决定下一个输出是以什么.
- 纯粹的Attention机制并不能提供时序数据之间的位置信息, Transformer就是一个很好的例子.
可视化分析
如果将上述输入$x_t$ 对输出$y_t$ 的权重$a_{t}(s)$ 做一张热力图, 就能看出当预测某个单词时, 对句子其他部分的侧重程度, 也就是注意力:
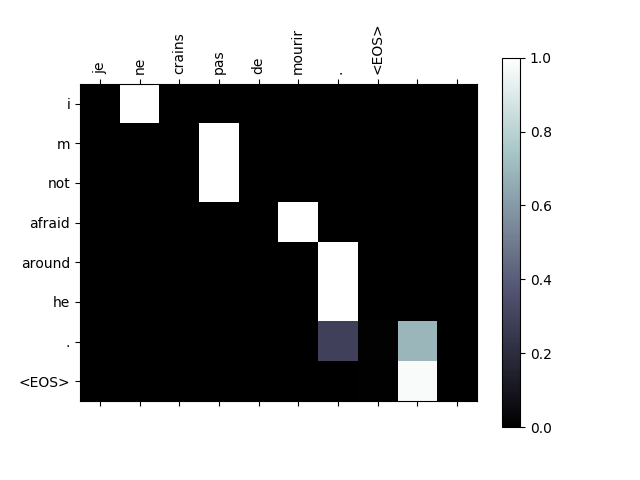
能很明显的看出, 当翻译某个词时, 不考虑语态的情况下, 翻译和它邻近的几个词有强大的联系, 这也就是Attention的最直观体现.
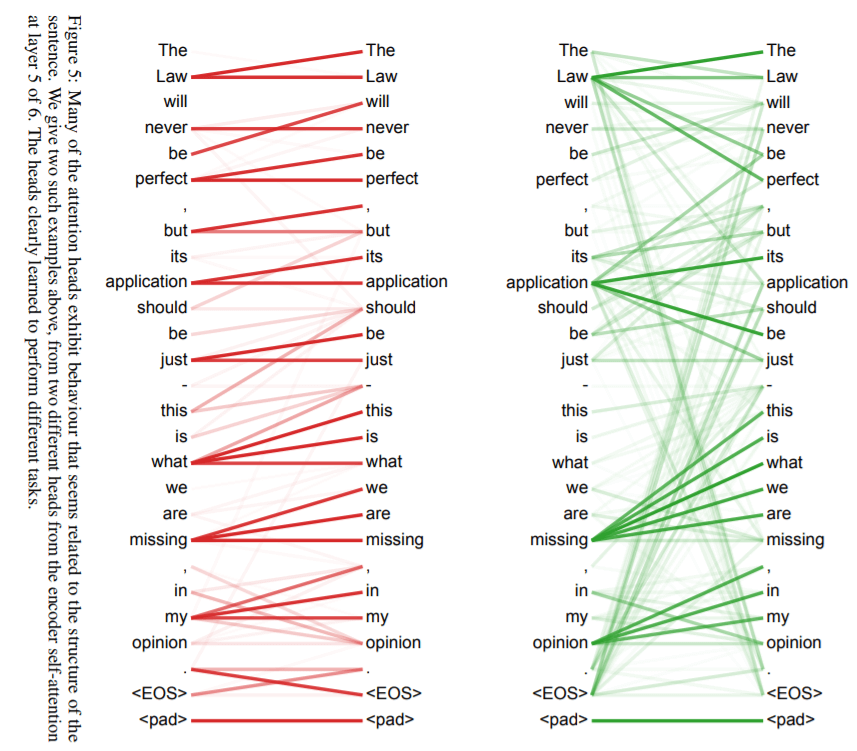
下图揭露了句子中前后单词之间的联系, 颜色深浅表示联系的强弱, 并且对于不同的任务, Attention能够学习到不同的注意力结构. 图片出自Attention Is All You Need(也是Transformer的论文).
在CV中, Attention同样有它的作用, 图片出自Show, Attend and Tell.

向RNN加入额外信息
Attention机制其实就是将的Encoder的隐藏层状态加权后获得权重向量$c_t$, 额外加入到Decoder中, 从而使得网络有更完整的信息流.
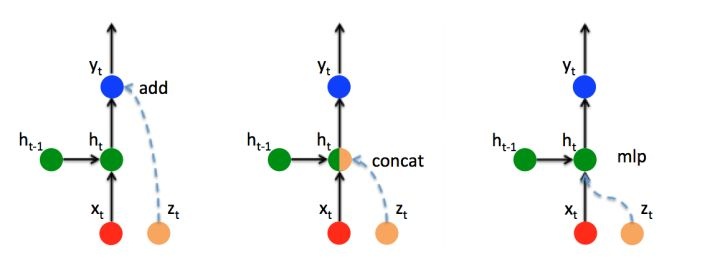
如果有额外信息$z_t$ 想要添加到Decoder中, 那么主要有以下三种方式:
Add: 直接将额外信息$z_t$ 叠加在输出$y_t$ 上.
$$
y_{t} \leftarrow y_{t}+z_{t}
$$Concat: 将额外信息$z_t$ 拼接在隐藏层的隐藏装填$h_t$, 然后通过全连接恢复维度, luong attention中就是用的这种方法.
$$
h_{t} \leftarrow W_{c} \cdot \operatorname{concat}\left(h_{t}, z_{t}\right)
$$Mlp: 直接添加一个对额外信息$z$ 的神经层.
$$
\begin{array}{l}
h_{t}^{z h}=W_{z h} \cdot z_{t}+b_{z h} \\
h_{t} \leftarrow \tanh \left(h_{t}^{i h}+h_{t}^{h h}+h_{t}^{z t}\right) \\
\quad=\tanh \left(\left(W_{i h} \cdot x_{t}+b_{i h}\right)+\left(W_{h h} \cdot h_{t-1}+b_{h h}\right)+\left(W_{z h} \cdot z_{t}+b_{z h}\right)\right)
\end{array}
$$

