发布日期: 2020-12-10

更新日期: 2022-03-27

文章字数: 2.6k

阅读时长: 10 分

本文前置知识:
Self - Attention: 详见Transformer精讲.
2020.12.14: 修正错误.

A Relational Memory-based Embedding Model for Triple Classification and Search Personalization

本文是论文A Relational Memory-based Embedding Model for Triple Classification and Search Personalization的阅读笔记和个人理解.

Basic Idea

作者认为, 现在的KGE方法普遍在记忆有效的三元组问题上受限, 并不能有效的捕捉三元组之间的潜在依赖关系.

现在的KGE普遍都用Link Prediction评估模型的性能, 但在实际应用中, 经常以三元组分类和个性化搜索为主要目标. 所以作者希望通过记忆提升这两个场景中的KGE性能, 关系记忆能够编码关系三元组之间的潜在依赖关系.

作者给出以下问题的定义:
三元组分类: 判断给定的三元组是否有效.
个性化搜索: 针对用户给出的请求, 对系统给出的搜索结果进行重排.

R - MeN

在R - MeN中, 作者考虑将三元组视为一个长度为3的时序序列看待, 通过Self - Attention对记忆循环交互.

整体流程是Embedding -> Memory Attention interact -> CNN decode:

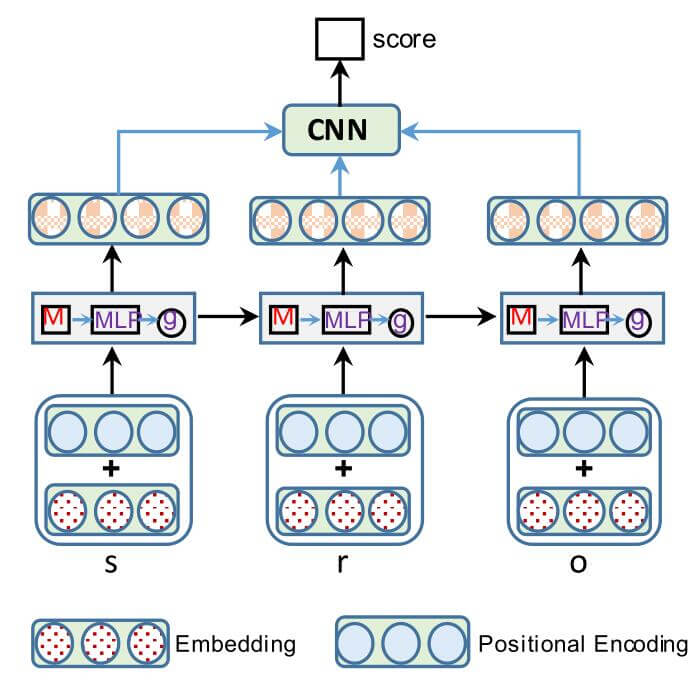
Positional Encoding

作者假设三元组$(s, r, o)$ 的相对位置关系对于推断三元组是否有效是十分必要的, 因此需要在三元组输入之前对它们都加以位置编码, 用$\mathbf{v}_{s}, \mathbf{v}_{r}, \mathbf{v}_{o} \in \mathbb{R}^{d}$ 分别代表$s,r,o$ 的嵌入, 加上位置编码后, 再经过一次线性变换的三元组向量$\left\{\mathbf{x}_{1}, \mathbf{x}_{2}, \mathbf{x}_{3}\right\}$ 为:
$$
\begin{aligned}
\mathbf{x}_{1} &=\mathbf{W}\left(\mathbf{v}_{s}+\mathbf{p}_{1}\right)+\mathbf{b} \\
\mathbf{x}_{2} &=\mathbf{W}\left(\mathbf{v}_{r}+\mathbf{p}_{2}\right)+\mathbf{b} \\
\mathbf{x}_{3} &=\mathbf{W}\left(\mathbf{v}_{o}+\mathbf{p}_{3}\right)+\mathbf{b}
\end{aligned}
$$
其中$\mathbf{W} \in \mathbb{R}^{k\times d}$ 为权重矩阵, $\mathbf{p}_{1}, \mathbf{p}_{2} \mathbf{p}_{3} \in \mathbb{R}^{d}$ 分别它们的位置编码, 其中的$k$ 代表每个Memory Slot的维度大小(下文会提到). 在文中, 并没有提及位置编码的实现方式.

Memory

作者假设有一个记忆$M \in \mathbb{R}^{N \times k}$, 它是由$N$ 行Memory Slot组成的, 每个Slot的大小为$k$. 用$M^{(t)}$ 代表$t$ 时刻的$M$ 矩阵, 那么$M_{i,:}^{(t)} \in \mathbb{R}^{k}$ 就代表其中第$i$ 个Memory Slot在$t$ 时刻存储的所有Memory.

那么每个Memory Slot中的记忆就一定会根据在$t$ 时刻的新输入$\mathbf{x}_t$ 来更新当前时刻的记忆$\hat{M}_{i,:}^{(t+1)}$.

如果使用跟Transformer中的多头类似的机制, 对每个Slot中的Memory进行分割:
$$
\hat{M}_{i,:}^{(t+1)}=\left[\hat{M}_{i,:}^{(t+1), 1} \oplus \hat{M}_{i,:}^{(t+1), 2} \oplus\right.\left.\ldots \oplus \hat{M}_{i,:}^{(t+1), H}\right]
$$
其中$\oplus$ 代表Concat操作, $H$ 代表总头数.

每个头的记忆$\hat{M}_{i,:}^{(t+1), h}$ 使用Self - Attention将过去时刻的记忆与当前时刻输入加权交互:
$$
\hat{M}_{i,:}^{(t+1), h}=\alpha_{i, N+1, h}\left(\mathbf{W}^{h, V} \mathbf{x}_{t}\right)+\sum_{j=1}^{N} \alpha_{i, j, h}\left(\mathbf{W}^{h, V} M_{j,:}^{(t)}\right)
$$
其中$\mathbf{W}^{h, V} \in \mathbb{R}^{n \times k}$ 是Value的投影矩阵, $n$ 是每个头的大小, 满足$k = nH$, 这样能保证Concat后的记忆矩阵中每个Slot的大小仍然是$k$ 维. $\left\{\alpha_{i, j, h}\right\}_{j=1}^{N}, \alpha_{i, N+1, h}$ 是注意力权重. 具体细节在下一小节介绍.

三元组中的三个元素被分别输入后, 记忆将被清除.

Self - Attention Interaction

与Self - Attention大同小异, 但在记忆存储机制的影响下, 归一化一定要包含过去记忆和当前时刻新输入两个部分:
$$
\begin{aligned}
\alpha_{i, j, h} &=\frac{\exp \left(\beta_{i, j, h}\right)}{\sum_{m=1}^{N+1} \exp \left(\beta_{i, m, h}\right)} \\
\alpha_{i, N+1, h} &=\frac{\exp \left(\beta_{i, N+1, h}\right)}{\sum_{m=1}^{N+1} \exp \left(\beta_{i, m, h}\right)}
\end{aligned}
$$
$\beta_{i, j, h}$ 是Attention得分, 也分别对应着过去记忆和当前时刻新输入两部分:
$$
\begin{aligned}
\beta_{i, j, h} &=\frac{\left(\mathbf{W}^{h, Q} M_{i,:}^{(t)}\right)^{\top}\left(\mathbf{W}^{h, K} M_{j,:}^{(t)}\right)}{\sqrt{n}} \\
\beta_{i, N+1, h} &=\frac{\left(\mathbf{W}^{h, Q} M_{i,:}^{(t)}\right)^{\top}\left(\mathbf{W}^{h, K} \mathbf{x}_{t}\right)}{\sqrt{n}}
\end{aligned}
$$
其中$\mathbf{W}^{h, Q} \in \mathbb{R}^{n \times k}$ , $\mathbf{W}^{h, K} \in \mathbb{R}^{n \times k}$ 分别是Query和Key的投影矩阵. 此外, 还在$\mathbf{x}_{t}$ 和$\hat{M}_{i,:}^{(t+1), h}$ 之间添加了Residual Connection和MLP, Gating, 具体添加方式作者未说明, 应该和关系记忆网络一致:

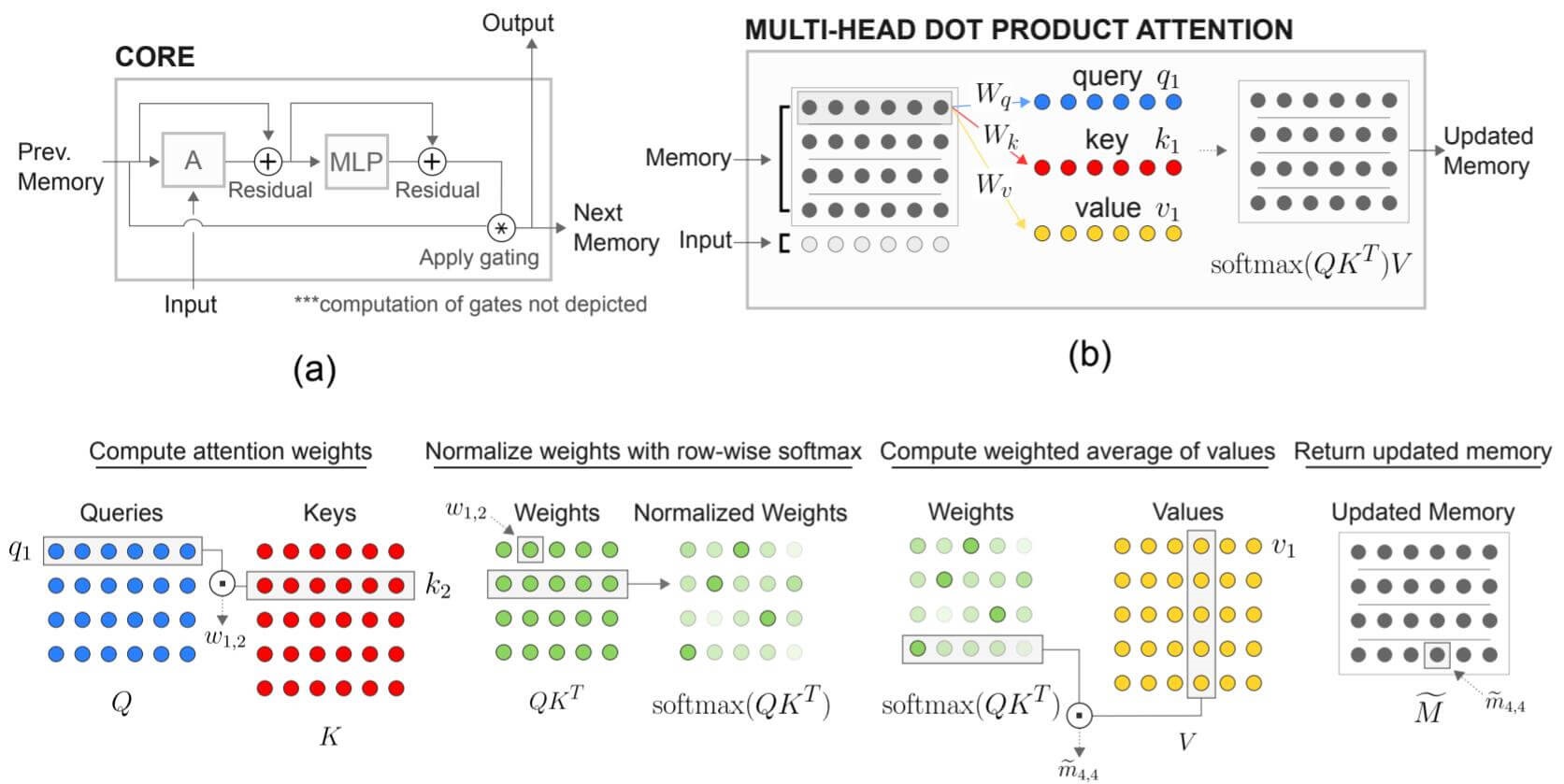
图片来自于关系记忆网络的论文Relational recurrent neural networks.

对于输入$\mathbf{x}_t$ 的最后编码产生的结果记为$\mathbf{y}_t \in \mathbb{R}^k$.

Score Function

将之前得出的$\left\{\mathbf{y}_{1}, \mathbf{y}_{2}, \mathbf{y}_{3}\right\}$ Concat起来, 接着用一个基于CNN的Decoder来解码:
$$
f(s, r, o)=\max \left(\operatorname{ReLU}\left(\left[\mathbf{y}_{1}, \mathbf{y}_{2}, \mathbf{y}_{3}\right] \ast \mathbf{\Omega}\right)\right)^{\top} \mathbf{w}
$$
$\left[\mathbf{y}_{1}, \mathbf{y}_{2}, \mathbf{y}_{3}\right] \in \mathbb{R} ^ {k \times 3}$, $\Omega$ 代表大小为$\mathbb{R} ^ {m \times 3}$ 的卷积核集合, 其中$m$ 为卷积核的窗口大小, $\ast$ 代表卷积操作. $\mathbf{w} \in \mathbb{R}^{\left| \Omega \right|}$ 是一个权重向量, 能将所有卷积核卷积得到的结果变成标量(其实就是得分). $\operatorname{max}$ 在这里代表最大池化. 作者认为这样能捕捉Feature map中的最重要特征, 并减小参数量.

Loss Function

采用Adam优化, 损失函数如下:
$$
\mathcal{L}=\sum_{(s, r, o) \in\left\{\mathcal{G} \cup \mathcal{G}^{\prime}\right\}} \log \left(1+\exp \left(-t_{(s, r, o)} \cdot f(s, r, o)\right)\right)
$$
其中$t_{(s, r, o)}$ 是一个符号函数:
$$
t_{(s, r, o)}=\left\{\begin{array}{l}
1 \text { for }(s, r, o) \in \mathcal{G} \
-1 \text { for }(s, r, o) \in \mathcal{G}^{\prime}
\end{array}\right.
$$
其中$\mathcal{G}$ 代表正确的知识图谱, $\mathcal{G}^{\prime}$ 代表被替换后污染的知识图谱(负例的知识图谱, 其中包含负例三元组).

Experiments

作者主要面向实际应用中比较多的三元组分类和个性化搜索两个任务进行实验. 详细的模型参数设置请参考原论文.

Triple Classification

三元组分类的问题是给定一个三元组, 通过模型来判断它们是否有效. 作者在WN11和FB13数据集上测试了R - MeN的三元组分类性能. 结果取决于一个阈值$\theta_r$, 如果高于阈值则视为三元组有效, 否则无效.

虽然前面介绍的Memory可以包含多个Slots, 但通过实验后, 作者发现对于所有的数据集, Memory Slot为1的时候效果都是最好的. 所以在之后的实验中只考虑使用单一的Memory Slot.

如果Memory Slot = 1, 关系记忆网络应该类似于GRU, 感觉有点退化的意思. 我始终没有想明白Single slot能work的理由.

实验结果如下:

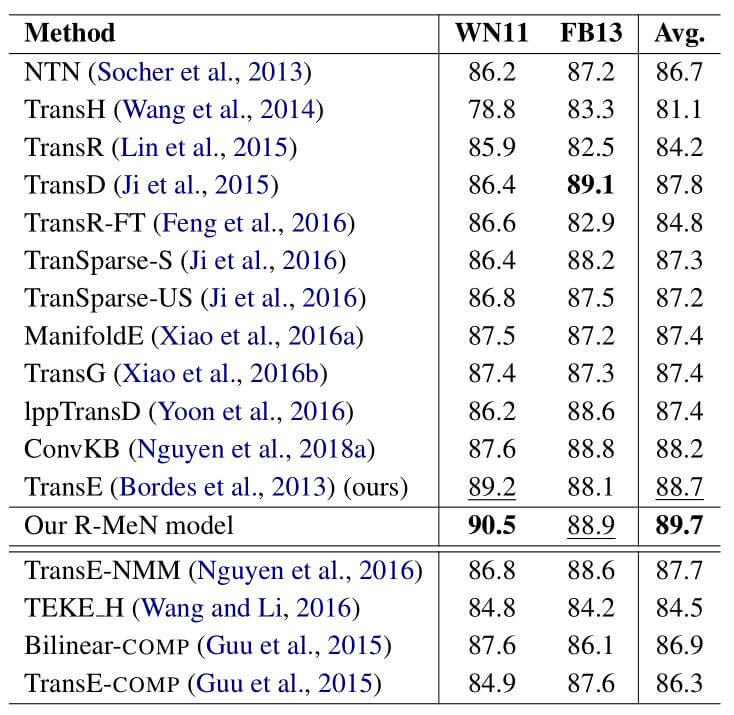
其中下划线代表效果次高的模型, 最下面一栏是借助了关系路径推理的模型.

R - MeN在这两个数据集上平均表现最好, 并且比TransE要好许多.

作者将TransE和R - MeN在WN11和FB13上针对关系的准确率进行了对比:

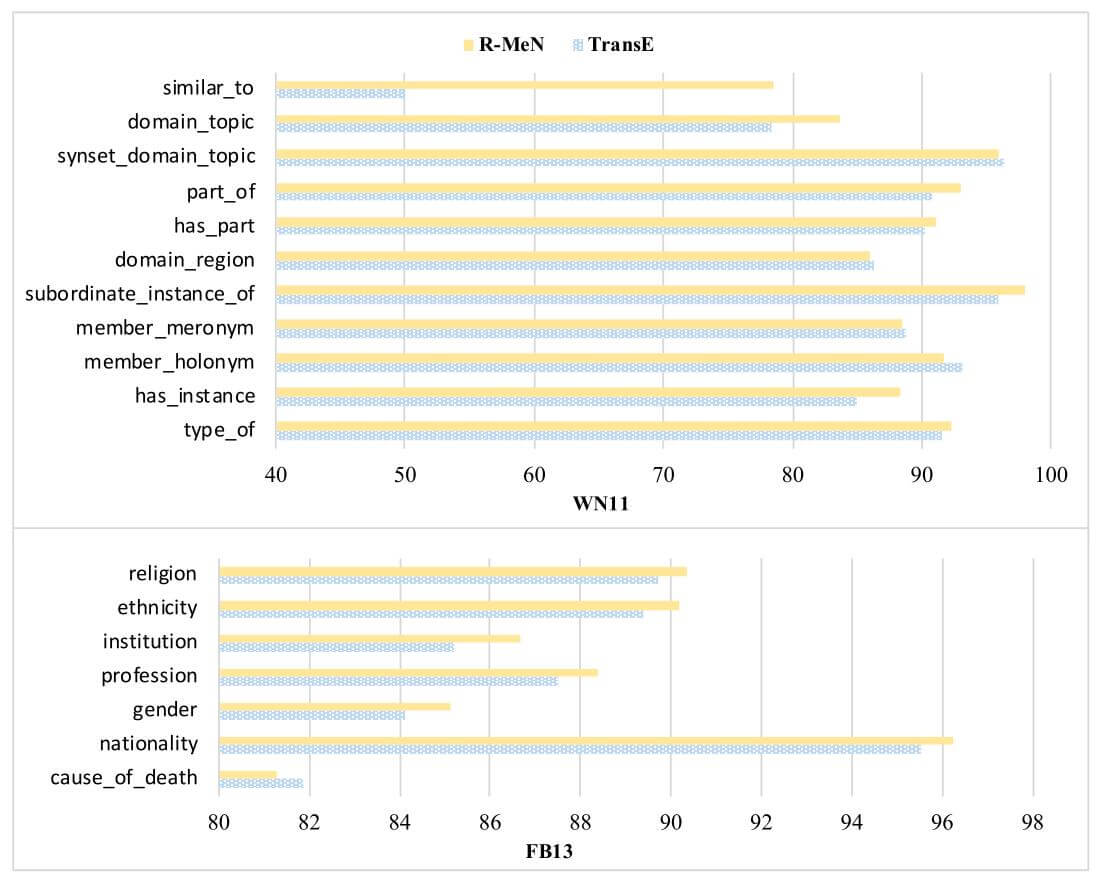
在WN11中, 对于一对一的关系similar_to, R - MeN比TransE有非常强的学习能力. 在作者给出的FB13关系准确率中, R - MeN比TransE要好.

Search Personalization

个性化搜索的问题被定义为根据用户给出的搜索请求, 目标是根据搜索系统给出的搜索结果进行重排. 这个搜索场景能被视为是三元组$(query, user, document)$, 所以R - MeN也能用于个性化搜索任务上.
作者在SEARCH17数据集上进行了实验, 结果如下:

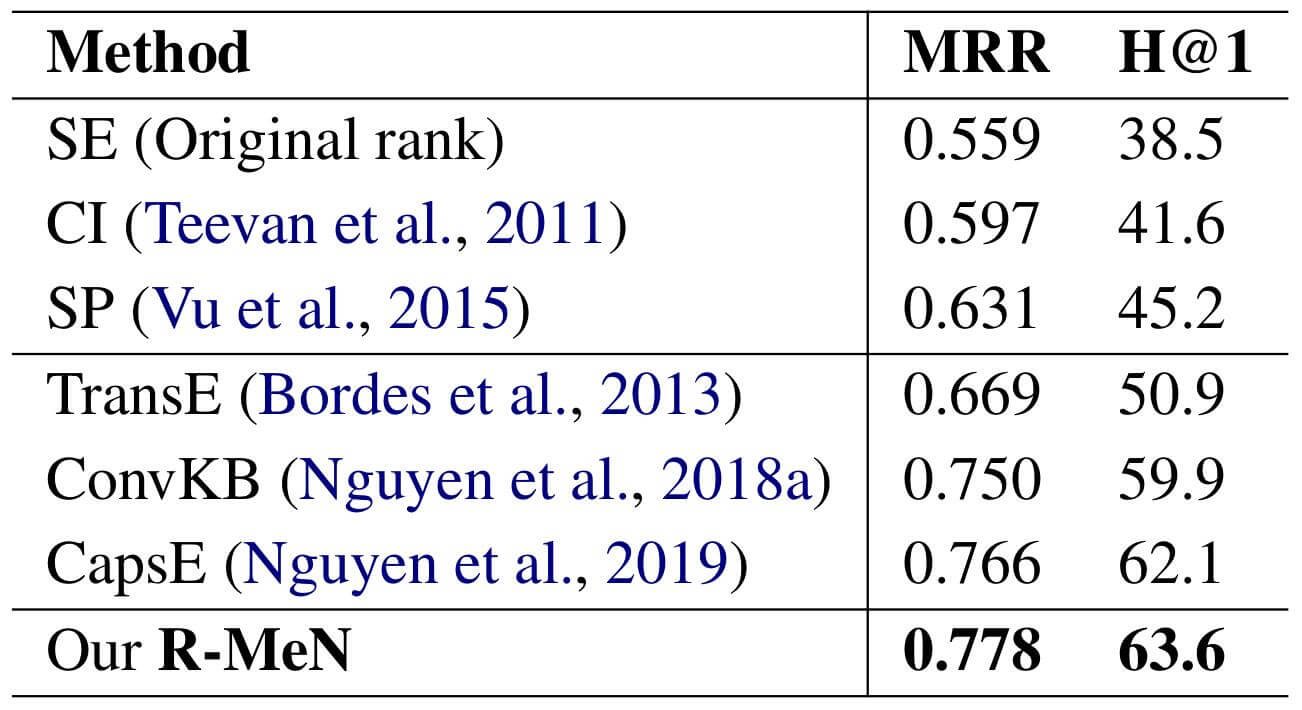
KGE方法在个性化搜索任务上比传统方法要好一些, R - MeN显示出更好的性能.

Effects of Hyper-Parameters

作者将多头的头大小$n$, 头的个数$H$ 在各个数据集上的性能进行对比:

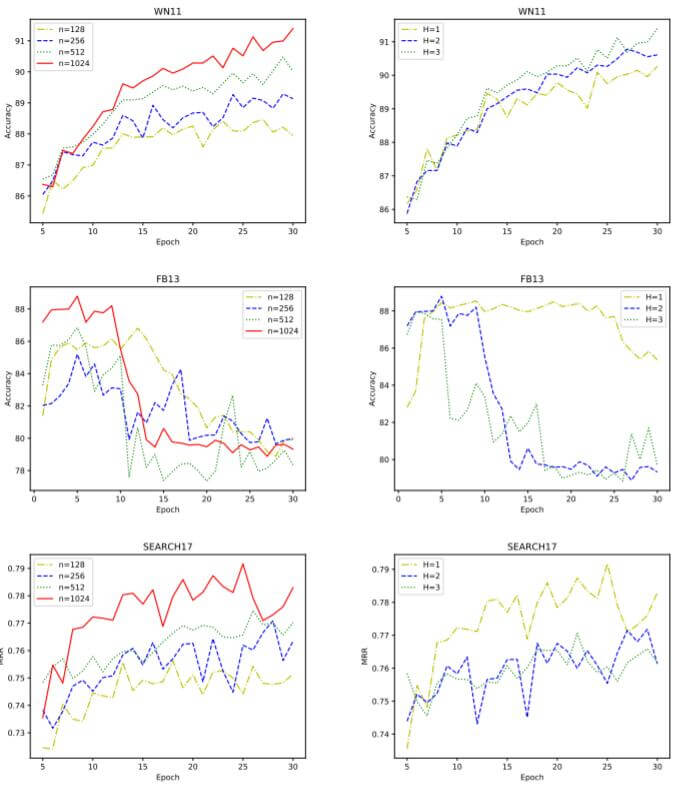
在三个数据集上, 使用更大的头有利于性能提升. 而在头的个数上, WN11和FB13中使用多头效果要更好, 在SEARCH17中单头效果更好, 作者认为SEARCH17是单意图的, 所以通常用1个头的效果会比较好. 因为头越多, 注意力就越分散, 就越容易Over Fitting.

Ablation Analysis

在消融实验中, 作者尝试去掉R - MeN的位置编码, 不使用关系记忆网络:

在不使用关系记忆网络时, 打分函数直接就变为了接收最原始的实体和关系Embedding $\mathbf{v}_{s}, \mathbf{v}_{r}, \mathbf{v}_{o}$ 作为输入:
$$
f(s, r, o)=\max \left(\operatorname{ReLU}\left(\left[\mathbf{v}_{s}, \mathbf{v}_{r}, \mathbf{v}_{o}\right] \ast \mathbf{\Omega}\right)\right)^{\top} \mathbf{w}
$$
去掉位置编码后, 在SEARCH17上的表现退化比较大, WN11没有变化, FB13有一点点下降. 在不使用关系记忆网络时, 所有性能都有退化, 关系记忆网络体现出比较大的作用.