本文前置知识:
- CNN: 详见卷积神经网络小结.
本文着重介绍深度可分离卷积和分组卷积两种操作.
深度可分离卷积
深度可分离卷积(Depthwise Separable Convolution)应用在MobileNet和Xception中. 似乎这二者的实现略有不同, 但二者的出发点都是通过深度可分离卷积来减少参数量.
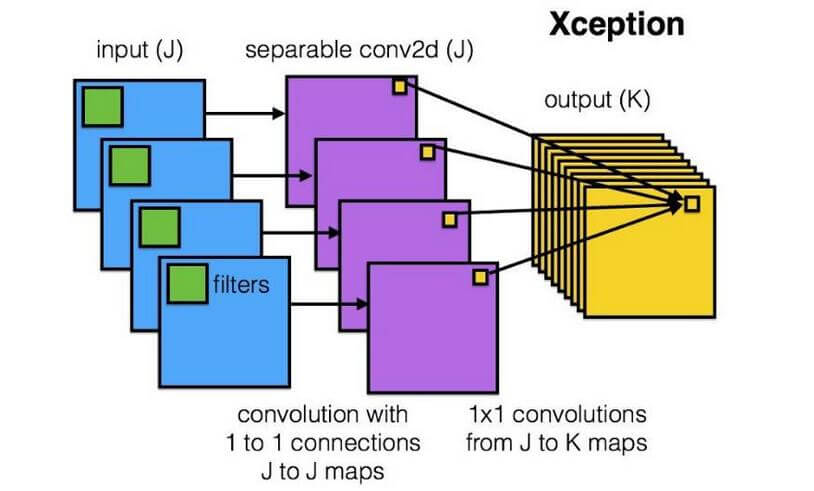
该图片出自zhihu(找不到最开始的原出处了).
我们来举一个例子说明深度可分离卷积是怎样运算的.
如果我们使用四个标准的卷积对下面的RGB三通道图像数据$C \times H \times W$ 进行卷积操作, 卷积后的通道数(或者说特征图个数)取决于卷积核的个数, 在这里生成了四张特征图.
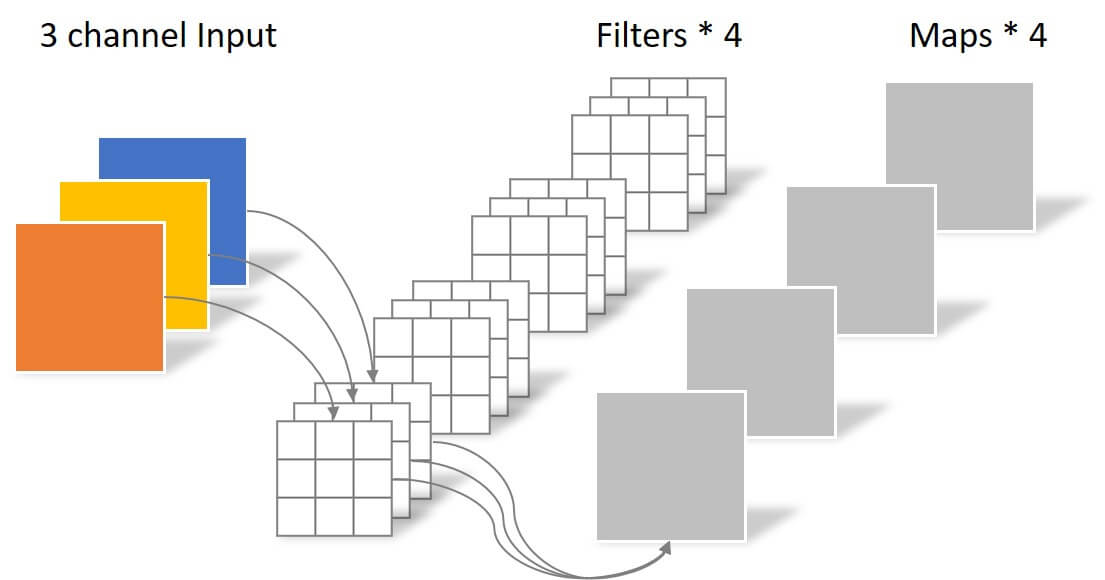
本小节其余图片出自卷积神经网络中的Separable Convolution.
卷积核在不同的通道上使用了不同的权重, 卷积核的大小可以看成是三维的$d_c \times k_h \times k_w$. 还有没有其他方法能达到等效或近似的效果呢? 在VGG中出现过类似的方法, 一个大卷积核可以被多个小卷积核近似表达.
$1\times 1$ 卷积能不改变特征图的大小, 利用这个特性, 深度可分离卷积将卷积拆成两步来做, 分别是深度卷积和分离卷积. 即使拆成两步, 最后能拿到的特征图大小也与标准卷积相同.
深度卷积
深度卷积(Depthwise Convolution)也可以称为逐通道卷积. 假设用$3\times 3 $ 大小的卷积核去卷积, 我们只对每个通道分别进行卷积, 而不是一起进行卷积:
逐通道卷积这一步中, 每个卷积核只有二维参数, 即$k_h \times k_w$ 个参数. 生成并能生成$C$ 张宽高变化后的特征图. 深度卷积只是单纯的分别运用了每个平面空间上的信息, 还没有将它们整合到一起, 即没有进行Channel维运算.
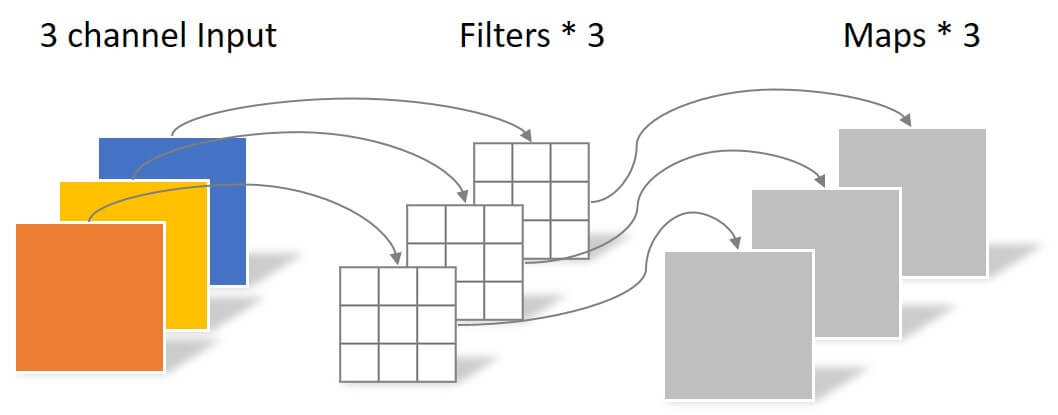
分离卷积
分离卷积(Separable Convolution)也称为逐点卷积. 其核心就是利用$1\times 1$卷积在不改变特征图大小情况下任意更改Channel数量的特性, 对Channel信息进行整合. $1\times1$ 卷积核有多少个, 就有多少特征图产生. 假设有$M$ 个$1\times1$ 卷积核, 就能生成$M$ 张宽高不变的特征图:

此时的$1 \times 1$ 卷积与标准卷积无异, 将贯穿于每一个Channel, 这样就完成了Channel维度上的信息整合. 经过深度卷积和分离卷积两步后, 其产生的特征图大小和使用四个$3\times3\times3$ 大小的标准卷积产生的结果无异.
参数量分析
更一般的, 假设图像大小为$C \times H \times W$, 使用$N$ 个$K \times K$ 的卷积核. 那么标准卷积所使用的参数量$P_{std}$ 为:
$$
P_{std} = K \times K \times C \times N = K^2\times C \times N
$$
而深度可分离卷积的参数量$P_{ds}$ 由两部分组成:
- Depthwise Convolution: 由于卷积核没有在Channel上的维度, 所以只使用了$K \times K \times N$ 个参数.
- Separable Convolution: 该部分是$1\times1$ 卷积的参数, 使用了$1\times1\times C \times N$ 个参数.
综上, 深度可分离卷积参数量为:
$$
P_{ds} = K \times K \times N + 1\times1\times C \times N = (K^2+C) \times N
$$
故深度可分离卷积与标准卷积的参数比为:
$$
\frac{P_{ds}}{P_{std}} = \frac{(K^2+C)\times N}{K^2 \times C \times N} = \frac{1}{C} + \frac{1}{K^2}
$$
参数量大量的减少了, 效率也提高了(详见Mobilenet).
分组卷积
分组卷积(Group Convolution)早在AlexNet中就出现了, AlexNet当时受算力的限制, 不能将整张图片直接读入GPU中, 所以对一张图片分割处理, 最后再整合起来:
假设我们要使用$c_2$ 个卷积核对$c_1\times H \times W$ 的图片进行卷积.
对于标准卷积, 使用的卷积核大小为$c_1\times h_1 \times w_1$:
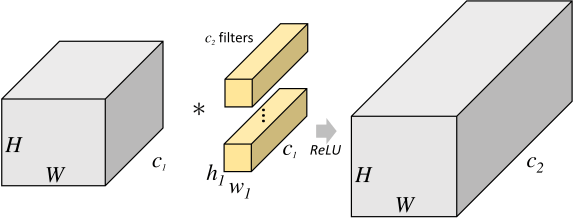
所产生的总参数量为$ c_1 \times h_1 \times w_1 \times c_2$.
如果将图片在Channel上分为$g$ 组, 分别只在$g$ 组上使用深度更小的卷积核分别进行卷积, 最后拼凑起来, 就称为了分组卷积:
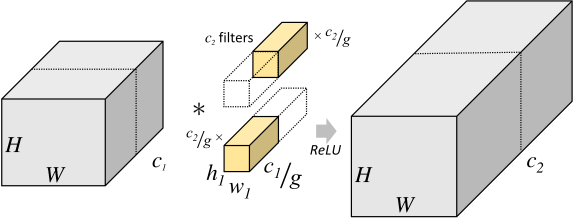
如图所示, 分组卷积所产生的总参数量为$g \times h_1 \times w_1 \times \frac{c_1}{g} \times \frac{c_2}{g}$, 即分组卷积产生的参数量为标准卷积参数量的$\frac{1}{g}$ 倍.
当分组数量$g$ 与Channel数相同, 即$g = c_1$ 时, 分组卷积就等价于前面说过的深度卷积(Depthwise Convolution). 因为只是最后将Channel维上的特征图Concat起来, 而没有进行交互, 所以在不同的Group之间, Channel维上的信息是没有得到整合的. 如果分组卷积只作为CNN的中间部件, 在后续的结构中可以使用其他整合的方式.

