发布日期: 2022-09-22

更新日期: 2023-11-05

文章字数: 4.4k

阅读时长: 17 分

UniRE: A Unified Label Space for Entity Relation Extraction

本文是论文UniRE: A Unified Label Space for Entity Relation Extraction 的阅读笔记和个人理解, 论文来自ACL 2021.

Basic Idea

作者认为现有的ERE模型经常将标签空间分为实体检测和关系分类两个子空间, 这样做会缺失实体和关系的交互. 作者希望使用一个统一的标签空间来消除两个子空间之间的差别对待, 并通过填表法来在统一空间中将实体和关系同时抽取出来.

UniRE

Task Definition

对于给定的句子$s=x_1, x_2, \ldots, x_{|s|}$, ERE的目标是抽取出所有的实体$\mathcal{E}$ 和实体之间存在的关系$\mathcal{R}$.

每个实体$e$ 对应着一种预定义好的实体类型$e.\text{type} \in \mathcal{Y}_e$, 例如PER, GPE 等, 由单个或多个连续Token构成.

每种关系是一个由两个实体$e_{1,}e_{2}$ 和预定义好的关系$l \in \mathcal{Y}_r$ 构成的三元组$(e_{1,}e_{2,} l)$,

作者将ERE视为一个表填充问题. 对于句子$s$, 作者尝试维护一个表$T^{|s| \times |s|}$, 在表$T$ 中的每个单元格$(i, j)$ 都应该被打上一个标签$y_{i, j} \in \mathcal{Y}$, $\mathcal{Y}=\mathcal{Y}_e \cup \mathcal{Y}_r \cup\{\perp\}$, $\perp$ 代表没有关系存在.

对于每个实体$e$, 它在表上对应的单元格$y_{i, j}\left(x_i \in e.\text{span}, x_{j \in} e.\text{span} \right)$ 都应该被填上它的实体类型$e.\text{type}$.

对于实体之间的每种关系$r=(e_{1,}e_{2,}l)$, 它们之间对应的单元格$y_{i, j}\left(x_i \in e.\text{span}, x_{j \in} e.\text{span} \right)$ 应该被填充上关系$l$. 其他的所有单元格应该被填上$\perp$.

上述标注策略如下所示:

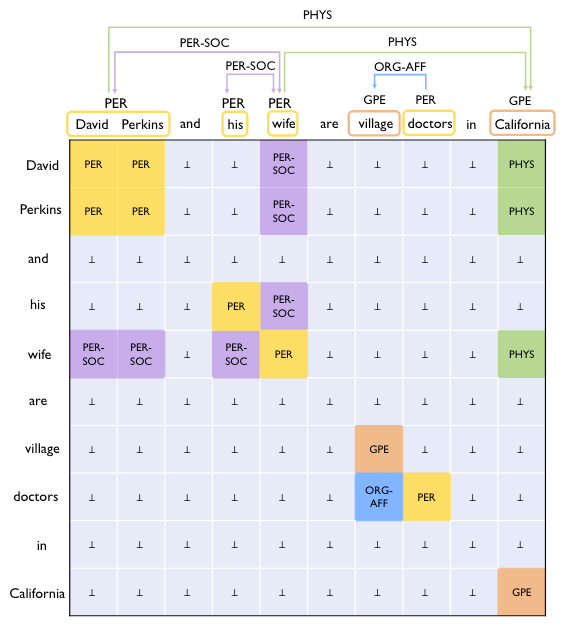
每个单元格都对应着一对Word. 作者注意到, 每个实体的标签都散落在对角线上, 并且是一个正方形, 关系是散落在对角线两侧的长方形.

在例子中, PER-SOC 是无向关系, PHYS 和ORG-AFF 都是有向关系, 这意味着它们在表上的标签是反对称的. 同时, 由于表实质是Word Pair的优势, 存在关系重叠也可以轻松地解决(RTE之前的挑战主要就是解决重叠问题). 如例子中David Perkins 被PHYS 和PER-SOC 所共享(在RTE里叫Single Entity Overlap), 但是仍然可以通过同行的不同列将这两种关系标注出来.

在测试阶段, 对实体关系的解码就变成了一个寻找长方形问题.

作者在这里简单的假设不存在重叠实体.

Biaffine Model

对于给定的输入句子$s$, 用BERT作为预训练语言模型PLM获得每个词的上下文表示$\mathbf{h}_i$, 那么句子中所有的Word表示为:

$$
\left\{\mathbf{h}_1, \ldots, \mathbf{h}_{|s|}\right\}=\operatorname{PLM}\left(\left\{\mathbf{x}_1, \ldots, \mathbf{x}_{|s|}\right\}\right)
$$

其中$\mathbf{x}_i$ 为每个Token$x_i$ 的输入表示(Embedding).

$\mathbf{h_i}$ 为文中每个词WordPiece后的首个Token的表示, 代替了每个词的表示作为Entity的分割边界, 这样可以减少不必要的输入和计算.

接着, 使用两个MLP对头尾角色(也就是表的行和列)做区分:

$$
\begin{aligned}
\mathbf{h}_i^{\text {head }}&=\operatorname{MLP}_{\text {head }}\left(\mathbf{h}_i\right)
\\
\quad \mathbf{h}_i^{\text {tail }}&=\operatorname{MLP}_{\text {tail }}\left(\mathbf{h}_i\right)
\end{aligned}
$$

其中$\mathbf{h}_i^{\text {head }} \in \mathbb{R}^{d,}\mathbf{h}_i^{\text {tail }} \in \mathbb{R}^d$ 分别为头尾的投影表示.

接着, 使用双仿射来计算表中每个单元格(Word Pair)的得分$\mathbf{g}_{i, j} \in \mathbb{R}^{|\mathcal{Y}|}$:

$$
\begin{aligned}
\mathbf{g}_{i, j} &=\operatorname{Biaff}\left(\mathbf{h}_i^{\text {head }}, \mathbf{h}_j^{\text {tail }}\right) \\
\operatorname{Biaff}\left(\mathbf{h}_1, \mathbf{h}_{\mathbf{2}}\right) &=\mathbf{h}_1^T \mathbf{U}_1 \mathbf{h}_2+\mathbf{U}_2\left(\mathbf{h}_1 \oplus \mathbf{h}_2\right)+\mathbf{b}
\end{aligned}
$$

其中$\mathbf{U}_{1}\in {|\mathcal{Y}| \times d \times d}, \mathbf{U}_{2}\in \mathbb{R}^{|\mathcal{Y} \times 2d|}, \mathbf{b} \in \mathbb{R}^{|\mathcal{Y}|}$ 为可训练参数, $\oplus$ 为拼接操作.

双仿射被认为是最深层次的Token Pair间交互方式, 最早用在依存分析里面, 现在基本上是NER SOTA的标配了.
虽然双仿射同时包含了加性和乘性, 但在Pytorch里仍然可以用torch.einsum 很简洁的实现, 如下:

class Biaffine(nn.Module):  
    def __init__(self, in_size, out_size, bias_x=True, bias_y=True):  
        super().__init__()  
        self.in_size = in_size  
        self.out_size = out_size  
        self.bias_x = bias_x  
        self.bias_y = bias_y  

        weight = torch.zeros((in_size + int(bias_x), out_size, in_size + int(bias_y)))  
        nn.init.xavier_normal_(weight)  
        self.weight = nn.Parameter(weight)  

    def forward(self, x, y):  
        if self.bias_x:  
            x = torch.cat([x, torch.ones_like(x[..., :1])], dim=-1)  
        if self.bias_y:  
            y = torch.cat((y, torch.ones_like(y[..., :1])), dim=-1)  
        hidden = torch.einsum("bxi,ioj,byj->bxyo", x, self.weight, y)  
        return hidden

关于该代码的推导可以参照这里:

Biaffine for NER：Named Entity Recognition as Dependency Parsing - 知乎

Table Filling

在有了表内单元格的打分$\mathbf{g}_{i, j}$ 后, 直接使用Softmax对单元格做多分类, 获得单元格内标签的概率$P\left(\mathbf{y}_{i, j} \mid s\right)$:

$$
P\left(\mathbf{y}_{i, j} \mid s\right)=\operatorname{Softmax}\left(\mathrm{dropout}\left(\mathbf{g}_{i, j}\right)\right)
$$

作者提到, 这里在Logits之前使用Dropout的技巧为模型性能带来了一点提升. 这种Trick称为Logits Dropout. 默认设为0.2.

然后使用多分类交叉熵优化:

$$
\mathcal{L}_{\text {entry }}=-\frac{1}{|s|^2} \sum_{i=1}^{|s|} \sum_{j=1}^{|s|} \log P\left(\mathbf{y}_{i, j}=y_{i, j} \mid s\right)
$$

其中$y_{i, j}$ 为表内的Golden Label.

Constraints

作者观察到, 表内的单元格并不是互相独立的, 上述分类器直接用上去就忽视了表内标签位置上的关联. 比如实体和无向关系在表内的标签总是正方形和长方形, 根据这个特性就令$\mathcal{P} \in \mathbb{R}^{|s| \times|s| \times|\mathcal{Y}|}$ 为表内所有单元格对应的标签概率的堆叠, 结合直观上的特性, 作者很直觉上的为模型加了两个约束Loss来帮助模型学习.

Symmetry

表内的实体标签和对称关系标签总是对称的. 所以对它们来说, 表格上的对称位置应该具有相同的标签概率分布. 添加一个表内的对称Loss$\mathcal{L}_{\mathrm{sym}}$:

$$
\mathcal{L}_{\mathrm{sym}}=\frac{1}{|s|^{2}} \sum_{i=1}^{|s|} \sum_{j=1}^{|s|} \sum_{t \in \mathcal{Y}_{\mathrm{sym}}}\mid \mathcal{P}_{i, j, t}-\mathcal{P}_{j, i, t}\mid
$$

$\mathcal{Y}_\text{sym}$ 代表对称的标签, 也就是实体类型标签和对称关系类型的集合.

在数据集中包含的对称标签如下:

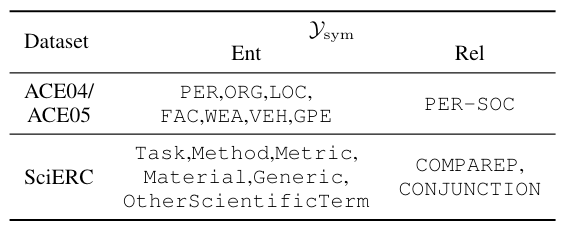
包含了所有的实体标签, 以及部分对称关系.

Implication

因为关系是基于实体的, 所以作者认为关系存在的概率不应该比实体存在的概率更大.

更直观点, 因为第$i$ 行和第$i$ 列对应的是某个Word和其他Word之间存在的关系, 该Word对应的所有关系标签$l$ 的概率$\mathcal{P}_{i,:, l}, \mathcal{P}_{:, i, l}$ 都不应该大于它自身(位于主对角线上)实体标签$t$ 的概率$\mathcal{P}_{i, i, t}$, 因此添加下述辅助Loss:

$$
\mathcal{L}_{\mathrm{imp}}=\frac{1}{|s|} \sum_{i=1}^{|s|}\left[\max _{l \in \mathcal{Y}_r}\left\{\mathcal{P}_{i,:, l}, \mathcal{P}_{:, i, l}\right\}-\max _{t \in \mathcal{Y}_e}\left\{\mathcal{P}_{i, i, t}\right\}\right]_\ast
$$

其中$[u]_{\ast}= \max(u, 0)$ 为Hinge Loss, 由于概率之间的差值本身就比较小, 所以也就不用添加Margin了.

Hinge Loss可以最大化这两类概率之间的差值, 也就是让关系的概率更小些, 实体类型的概率更大些.

最后简单的将主Loss和两个约束Loss相加即可:

$$
\mathcal{L}=\mathcal{L}_{\text {entry }}+\mathcal{L}_{\text {sym }}+\mathcal{L}_{\mathrm{imp}}
$$

至此, 模型的大致运行过程可以由下图概括:

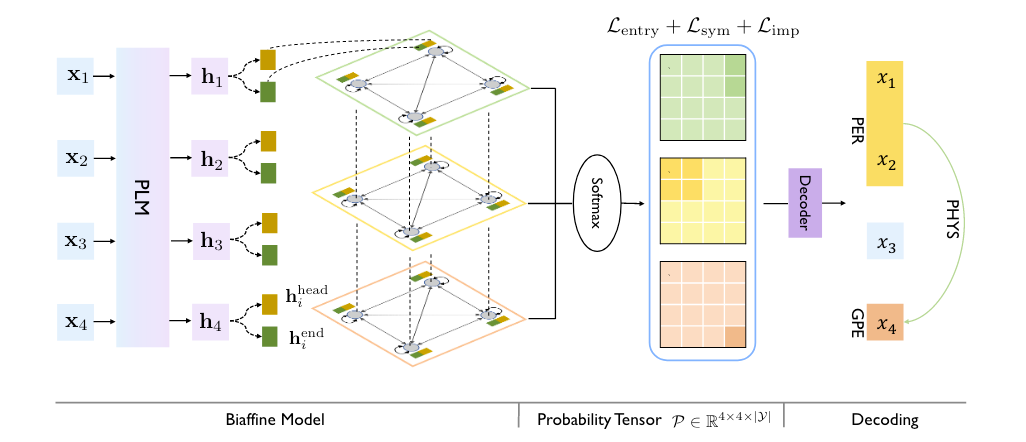
由PLM先抽取特征, 然后用双仿射得到一张将实体关系统一在同一空间下的表, 同时使用一个主Loss和两个辅助约束Loss对模型进行优化, 再由一种解码算法得到实体和关系.

Decoding

测试阶段需要根据$\mathcal{P} \in \mathbb{R}^{|s| \times|s| \times|\mathcal{Y}|}$ 进行解码, 作者希望这个解码算法能够做到又快又强.

作者使用了一种三步解码算法:

解码Span以识别实体边界.
解码实体的实体类型.
解码实体对的关系类型.

Span Decoding

作者观察到, 任何一个实体, 它所对应的行之间或列之间是完全一致的.

因为同一个实体所对应的多个行或多个列仍然归属于该实体本身, 所以它们对应的关系和实体标签是一致的.

因此, 当相邻行或相邻列不同时, 一定意味着有实体边界的产生.

基于上述观察, 作者将$\mathcal{P} \in \mathbb{R}^{|s| \times|s| \times|\mathcal{Y}|}$ 从行视角展平为二维矩阵$\mathcal{P}^\text{row} \in \mathbb{R}^{|s| \times (|s| \times|\mathcal{Y}|)}$, 计算相邻行之间的欧氏距离. 与行相对应的, 从列视角展平为二维矩阵$\mathcal{P}^\text{col} \in \mathbb{R}^{(|s| \times |\mathcal{Y}| ) \times |s| }$, 计算相邻列之间的欧氏距离. 最后将二个距离求平均, 作为最终距离, 当最终距离大于一个阈值$\alpha$ 的时候, 则判定该位置为切割点.

结合作者给出的示意图很好理解找实体边界(切割点)的思想:

这种对概率分布差求平均的解码方式很新颖啊, 也很取巧, 估计阈值$\alpha$ 的调整会对结果产生很大的影响(见后文实验).

作者通过这种方式将解码时间复杂度缩减到了$\mathcal{O}(|s|)$.

作者在脚注里偷偷写到, 在Inference阶段, 对于对称的标签$t \in \mathcal{Y}_{\text{sym}}$, 作者设置$\mathcal{P}_{i, j, t} = \mathcal{P}_{j, i, t} = (\mathcal{P}_{i, j, t} + \mathcal{P}_{j, i, t}) / 2$. 我认为这样做可以增大对称标签所对应的实体类型或关系类型的正确率, 对称关系或标签总是成对出现, 结合这种分割实体边界的分块思想, 更容易将块内实体或关系分类正确.

Entity Type Decoding

对于由Span Decoding给出的Span$(i, j)$, 实体类型$\hat{t}$ 由对角线上的对称的正方形中最大的实体类型概率得到:

$$
\hat{t}=\arg \max _{t \in \mathcal{Y}_e \cup\{\perp\}} \operatorname{Avg}\left(\mathcal{P}_{i: j, i: j, t}\right)
$$

若$\hat{t} \in \mathcal{Y}_e$, 则解码出实体, 若$\hat{t}=\perp$ 则认为Span$(i, j)$ 不是实体.

Relation Type Decoding

类似于实体类型的得出, 在得到Span$(i,j)$ 存在的实体$e_1$ 和Span$(m, n)$ 存在的实体$e_2$ 后, 关系类型$\hat{l}$ 也由相应的实体构成的长方形得到:

$$
\hat{l}=\arg \max _{l \in \mathcal{Y}_r \cup\{\perp\}} \operatorname{Avg}\left(\mathcal{P}_{i: j, m: n, l}\right)
$$

若$\hat{t} \in \mathcal{Y}_r$, 则解码出关系三元组$(e1, e2, \hat{l})$, 若$\hat{t}=\perp$ 则认为$e_{1,}e_2$ 间没有关系.

上述三步解码可以归结为下图:

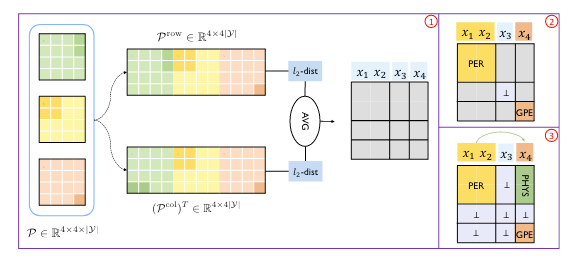
Experiments

详细的实验设置请参照原论文.

Datasets

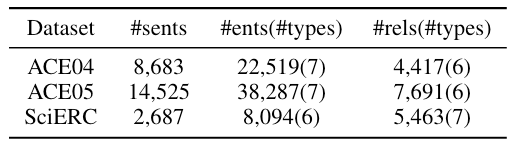
数据集是NER上常用的三个数据及ACE04 / 05和SciERC, 统计信息如下:

Performance Comparison

在这里关系预测使用的是严格评估, 也就是实体的边界, 类型, 以及它们之间的关系都正确时才算正确. 结果如下:

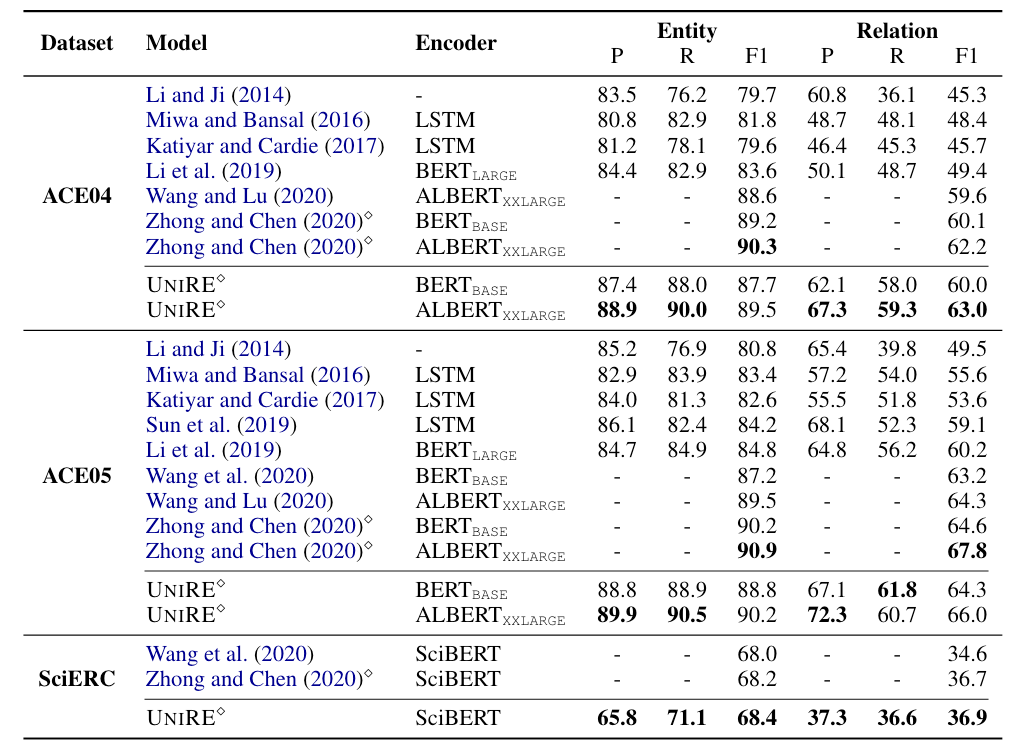
Wang et al.和Zhong and Chen分别对应着20年ERE方法TSE和PURE. UniRE在ACE05上的表现并没有PURE好, 但在更困难的SciERC上效果略好于PURE. 在ACE04上的表现比Baseline好得多.

由于关系预测使用的是严格标准, 所以关系预测任务难度要大得多, 整个ERE任务性能好不好应该看关系预测效果, 而不是实体抽取效果.

当使用BERT - base做PLM的时候, 在所有数据集上UniRE都是略差于PURE的, 有些小尴尬. 我认为这可能证明了在困难任务上, Joint Model需要更大的PLM底层的知识作为驱动.

Ablation Study

在ACE05和SciERC上的消融实验结果如下:

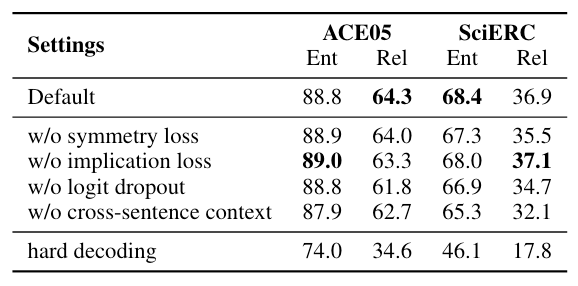
在没有辅助Loss约束的情况下, 其实UniRE已经可以作为一个比较好的Baseline了.

影响如下:

Symmetry Loss: 在ACE05上实体识别稍微掉了一点, 但是在SciERC上有明显涨点. 它对实体分类有效, 在两个数据集上似乎对关系分类也很有帮助的.
Implication Loss: 在ACE05上移除会有害于关系预测, 发挥了不小作用, SciERC上则是稍稍一点副作用.
Logit Dropout: 在两个数据集上, 使用Logit Dropout带来了两个点的提升.
Cross - Sentence Context: 像PURE里面一样, 也使用一个跨句的窗口来捕捉长距离依赖. 使用更大的上下文有益于任务.
Hard Decoding: 直接使用概率分布硬解码, 而不使用作者提出的解码算法. 对于正方形 / 长方形, 对应的实体类型 / 关系类型均取最高频次者. 如果直接硬解码, 效果会非常差, 证明了作者的解码方法有效.

Inference Speed

作者比较了UniRE与PURE在两个数据集上的性能和推理速度, 以及参数:

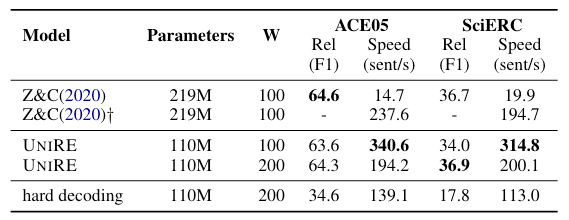
PURE因为采用了两个独立的Encoder所以参数量是UniRE的两倍. 从结果中可以看出, UniRE比PURE的近似模型推理速度快不少. 性能上不相上下.

Impact of Different Threshold α

在前文中提到过, 基于阈值的解码方法会因阈值大小而产生很大影响. 关于阈值的选取, 作者分析了ACE05验证集上的行距离分布, 如下:

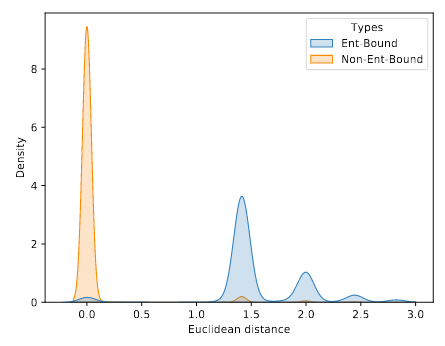
作者发现不是实体边界的地方几乎都集中在0附近, 也就是归于同一实体的不同行得到的概率分布是十分相似的, 而位于实体边界的行之间的欧氏距离位于1.4到1.5左右较多. 这大致可以说明作者的直觉是正确的.

光有直观的感觉还不太够, 还要具体的实验数据来论证, 在ACE05验证集上Span F1, Entity F1, Relation F1随阈值的变化如下:

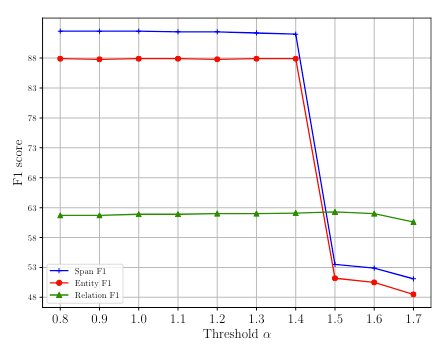
能够看到, 在阈值设定为1.4之前模型一直都有很稳定的表现, 而且表现得不错, 在将阈值设置为1.5时, Span F1和Entity F1直接有一个断崖式的下降. 也就是说当阈值大于1.5时边界将变得不再那么容易区分, 很多可以区分的实体都集中在1.4到1.5之间. Relation F1却下降的没有那么厉害, 作者认为是由于关系比较稀疏, 许多实体之间不存在关系, 所以关系受到的影响较小.

Context Window and Logit Dropout Rate

作者探究了不同的上下文滑窗大小和Logits Dropout Rate对性能的影响:

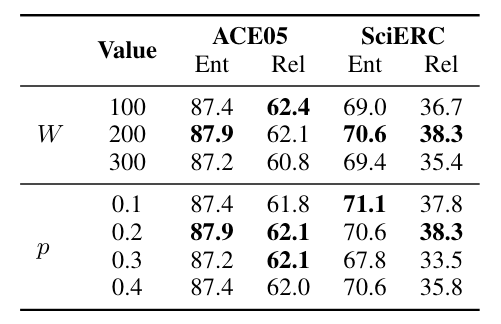
Logits Dropout对UniRE有一定帮助, 在Dropout概率为0.2时比较好.

Error Analysis

作者对预测结果做了错误分析, 将其分为五类错误:

Span Splitting Error(SSE): Span划分错误.
Entity not Found(ENF): 实体没预测出来.
Entity Type Error(ETE): 实体预测出来了, 但是实体类型找错了.
Relation not Found(RNF): 关系没有预测出来.
Relation Type Error(RTE): 关系预测出来了, 但是关系类型找错了.

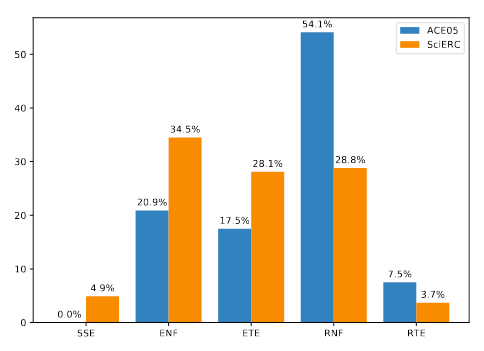
能从图中看到, SSE占得比例其实比较小, 说明作者的Span解码算法是很有效的. 实体和关系没找到的比例远远比类型预测错误要多, 作者认为是因为表中的类别不平衡问题仍然存在(毕竟表内大多的地方的标签都为$\perp$).

在文章最后, 作者给出了两个关于解码算法鲁棒性的例子:

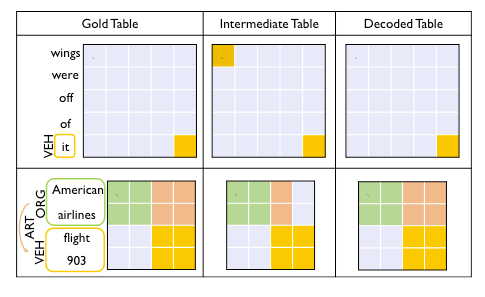
即使双仿射得出的模型预测Intermediate Table是有一部分错误的, 作者所提出的解码算法仍然能够抽取出正确的实体和关系.

第一个例子没太懂是怎么消除掉的, 第二个例子中, Intermediate Table的橘色部分虽然列视角第三列和第四列差异足够大, 但在行视角中四三行和第四行并没有差别, 所以没有被切割开, 因此解码后和Golden Label一致.

Summary

非常扎实而且有意思的一篇论文.

UniRE用一种统一标签, 尝试将ERE任务在一张实体关系统一表上用填表法解决, 理论上消除了实体空间和关系空间的偏差.

我认为无论是从表标签设计, 解码设计, 还是最后文中作者对模型中的阈值选取的分析等, 都是很有深度的.

尤为亮眼的是Span解码的方式设计, 使用了一种非常新颖的, 基于概率分布差再求平均的方式判断实体边界, 因为将实体和关系杂糅在一张表中, 所以本身UniRE的表内解码是非常容易出错的. 甚至可以说这个解码算法是驱动UniRE能做Work的源头.
作者在文末还展示出解码算法的鲁棒性打消读者的疑虑, 可以说是考虑的面面俱到了.

DaNing

https://ADAning.github.io/posts/8137.html