Two are Better than One: Joint Entity and Relation Extraction with Table - Sequence Encoders
本文是论文Two are Better than One: Joint Entity and Relation Extraction with Table-Sequence Encoders的阅读笔记和个人理解. 论文来自EMNLP 2020. 本文为RTE问题中, 探讨NER和RE任务间关系的系列三部曲中的第一篇.
Basic Idea
NER和RE是两个NLP里的基础任务, 最近联合学习的算法尝试把NER和RE同时解决, 很多算法都尝试用填表式一次性完成. 但是现有的算法大多采用的是单个Encoder, 把NER和RE放在同一个Encoder提供的空间捕获信息.
作者举了一个非常简单的例子:
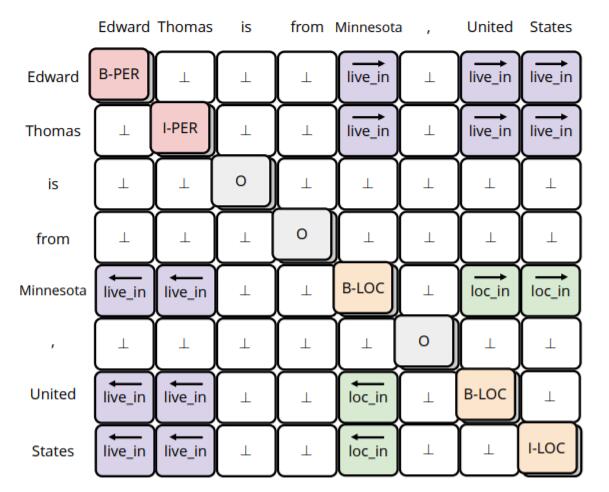
上图中, NER和RE在一张表中被一次性解决:
- 在主对角线中, 实体被BIO标注法标出, NER被完成.
- 在对角线两侧, 不同的颜色代表不同的关系, 而方向标明了该实体是Subject还是Object, RE被完成.
作者认为, 这样的设计是不符合联合学习的设计思想的, 必然会限制联合算法的效果:
- 存在特征困惑问题, 即One Feature for Two Task, NER和RE本来是两个不同的任务, 单个Encoder会在学习过程中产生困惑, 不能学习到同时解决NER和RE任务的特征.
- 没有充分使用表结构信息, 大多数的Joint Extraction论文确实构造了表结构, 但是却最后把Table Filling问题转化为一个Sequence Labeling问题去解决.
基于上述问题, 作者尝试在模型底层构建两个单独学习特征的Encoder, 分别学习NER和RE的特征.
TSE
TSE(Table - Sequence Encoders)是我自己给模型起的名字. 相较于后续其他论文起的Table - Sequence, 我还是认为简写更好.
作者眼中的NER和RE任务形式为:
- NER: NER被建模为一个序列标注问题, 其Label $\boldsymbol{y}^{\text {NER}}$ 为标准的BIO标注.
- RE: RE被建模为一个填表问题, 对于给出的句子$\boldsymbol{x}=\left[x_{i}\right]_{1 \leq i \leq N}$, 在标注表中标注出$\boldsymbol{y}^{\mathrm{RE}}=\left[y_{i, j}^{\mathrm{RE}}\right]_{1 \leq i, j \leq N}$. 实体$x_{i^{b}}, \ldots, x_{i^{e}}$ 与实体$x_{j^{b}}, . ., x_{j^{e}}$ 之间的关系定义为$y_{i, j}^{\mathrm{RE}}=\overrightarrow{r}$, 当两实体调换位置时, 记为$y_{j, i}^{\mathrm{RE}}=\overleftarrow{r}$. $\perp$ 代表不存在关系.
TSE主要由三个部分组成: 基础表示Text Embedder, 表表示Table Encoder, 序列表示Sequence Encoder:
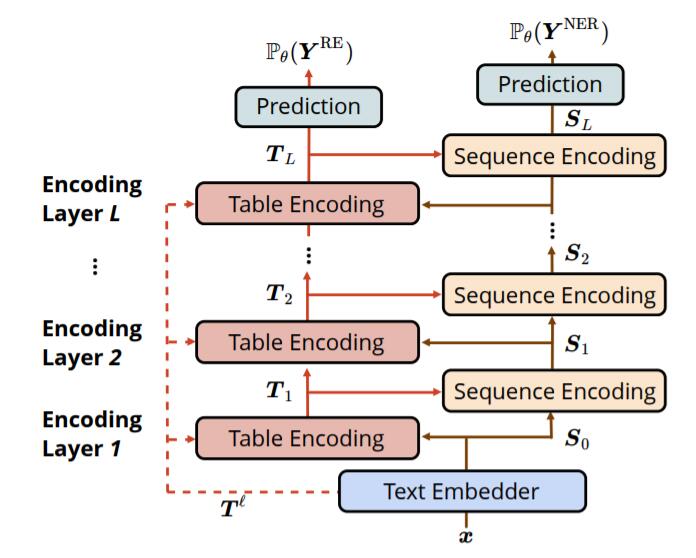
Text Embedder
句子中含有$N$ 个单词$\boldsymbol{x}=\left[x_{i}\right]_{1 \leq i \leq N}$, 句子中的Token表示分别由三类Embedding组成, 分别是Word Embedding, LSTM提取的Character Embedding, 以及BERT抽取的上下文相关的Contextualized Word Embedding.
句子级别的Token表示分别为$\boldsymbol{x}^w$, $\boldsymbol{x}^c$, $\boldsymbol{x}^l$. 句子表示$\boldsymbol{S}_0$如下:
$$
\boldsymbol{S}_{0}=\operatorname{Linear}\left(\left[\boldsymbol{x}^{c} ; \boldsymbol{x}^{w} ; \boldsymbol{x}^{\ell}\right]\right)
$$
即将三个Embedding拼接后直接变换, $\boldsymbol{S}_0 \in \mathbb{R}^{N \times H}$.
Table Encoder
Table Encoder专门学习表表示.
首先, 由Sequence表示构造表结构, 刚开始表是表内上下文无关的, 从第$l-1$ 层Sequence Encoder得到的Sequence表示中获取表第$i$ 行第$j$ 列所需的信息, 简单的用$\operatorname{Linear}$ 展开成一个表:
$$
X_{l, i, j}=\operatorname{ReLU}\left(\operatorname{Linear}\left(\left[S_{l-1, i} ; S_{l-1, j}\right]\right)\right)
$$
第$l$ 层Table Encoder有$\boldsymbol{X}_l \in \mathbb{R} ^{N \times N \times H}$.
接着, 采用多维RNN(MD - RNN)去迭代的融合表间信息, 也就是表内上下文相关的信息:
$$
T_{l, i, j}=\operatorname{GRU}\left(X_{l, i, j}, T_{l-1, i, j}, T_{l, i-1, j}, T_{l, i, j-1}\right)
$$
$\operatorname{GRU}$ 跨越了三个维度, 除了表的行$i$, 列$j$, 还有跨越不同Table Encoder层的$l$.
第$l$ 个Table Encoder的表中的第$i$ 行, 第$j$ 列的信息$T_{l, i, j}$ 由多个GRU捕获, 每个GRU可以捕获到不同信息:
$$
\begin{aligned}
&T_{l, i, j}^{(a)}=\operatorname{GRU}^{(a)}\left(X_{l, i, j}, T_{l-1, i, j}^{(a)}, T_{l, i-1, j}^{(a)}, T_{l, i, j-1}^{(a)}\right) \\
&T_{l, i, j}^{(c)}=\operatorname{GRU}^{(c)}\left(X_{l, i, j}, T_{l-1, i, j}^{(c)}, T_{l, i+1, j}^{(c)}, T_{l, i, j+1}^{(c)}\right) \\
&T_{l, i, j}=\left[T_{l, i, j}^{(a)} ; T_{l, i, j}^{(c)}\right]
\end{aligned}
$$
在表结构中, RNN可以选择递归方向, 对于式子中出现的$a, b, c, d$ 分别代表作者所尝试的方向, 示意图如下:
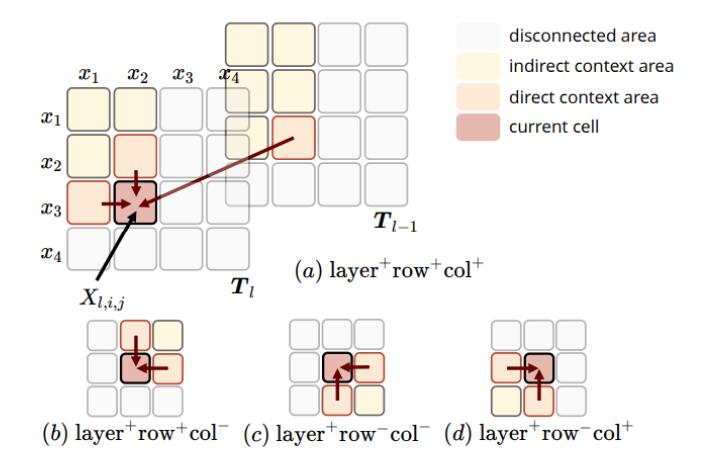
作者尝试了a, c组合和a, b, c, d组合两种设置, 后来发现前后二者差别不大, 所以采用简单的前者.
个人猜测应该是b, d信息冗余. 从a触发, 代表表行和列的顺向, 从c出发代表表行和列的逆向. 而b代表行的顺向, 列的逆向, d代表行的逆向, 列的顺向.
在我们所习惯的双向RNN中扩展到表结构上, 就是a, c的组合, 无需再重复添加b, d.
Sequence Encoder
Sequence Encoder专门学习序列表示.
作者认为单纯的缩放点积注意力在本模型中不够好, 于是提出了Table - Guided Attention, 用表信息指导Sequence中的Attention.
对于给定的$\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V}$, 一般的注意力可被下述式子概括:
$$
f\left(Q_{i}, K_{j}\right)=U \cdot g\left(Q_{i}, K_{j}\right)
$$
$f$ 能返回$Q_i$ 下$V_i$ 的权重. 其中$U$ 为可学习参数, $g$ 为计算$Q, K$ 间相关性的函数.
如下图所示:
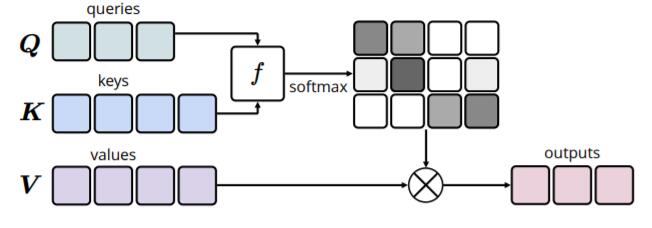
在本模型中, 恰好$\boldsymbol{Q}= \boldsymbol{K} =\boldsymbol{V}=\boldsymbol{S}_{l-1}$, 而$\boldsymbol{T}_l$ 是由$\boldsymbol{S}_{l-1}$ 得到的, 可以视为$T_{l, i, j} = g(S_{l-1, i}, S_{l-1, j}) = g(Q_i, K_j)$. 因此有:
$$
f\left(Q_{i}, K_{j}\right)=U \cdot T_{l, i, j}
$$
作者认为这种Attention有三个好处:
- 不用算$g(\cdot)$, 直接从Table Encoder里拿$\boldsymbol{T}_l$ 就行.
- 因为$\boldsymbol{T}_l$ 是表内上下文相关的, 所以更能捕捉词间不同相关性.
- 使得Table Encoder能参与到Sequence Encoder的学习过程中, 从而提升两个Encoder间的交互性.
其余的内容和Self - Attention一样:
$$
\begin{aligned}
\tilde{\boldsymbol{S}}_{l} &=\operatorname{LayerNorm}\left(\boldsymbol{S}_{l-1}+\operatorname{SelfAttn}\left(\boldsymbol{S}_{l-1}\right)\right) \\
\boldsymbol{S}_{l} &=\operatorname{LayerNorm}\left(\tilde{\boldsymbol{S}}_{l}+\operatorname{FFNN}\left(\tilde{\boldsymbol{S}}_{l}\right)\right)
\end{aligned}
$$
我再回来看一眼Table Encoder和Sequence Encoder之间迭代提升的过程:

注意, 在这个图左侧是有虚线的! 它的作用将在下一小节说明.
Exploit Pre - trained Attention Weights
作者认为, BERT的潜力没有被充分发掘, 因为BERT能很好的把握住词和词之间的关系, 所以Attention Weights最好被显式的加进来, 预训练模型的潜力就被更进一步的挖掘了.
作者把所有层的所有头的Attention Weights全部堆叠起来, 记为$\boldsymbol{T}^{l} \in \mathbb{R}^{N \times N \times (L^\ell \times A^\ell)}$, $L^{\ell}$ 为Transformer堆叠的层数, $A^\ell$ 为注意力头数.
接着只要把前面Sequence Encoder公式替换即可:
$$
\displaylines{X_{l, i, j}=\operatorname{ReLU}\left(\operatorname{Linear}\left(\left[S_{l-1, i} ; S_{l-1, j}\right]\right)\right)
\\
\downarrow
\\
X_{l, i, j}=\operatorname{ReLU}\left(\operatorname{Linear}\left(\left[S_{l-1, i} ; S_{l-1, j} ; T_{i, j}^{\ell}\right]\right)\right)}
$$
在每层生成Table表示的时候, 就必须考虑第$i$ 个词和第$j$ 个词之间的Attention Score $T_{i, j}^\ell$.
其余部分完全不用变, 就可以直接把预训练的BERT拿过来用.
再来回顾一下模型的整个流程:
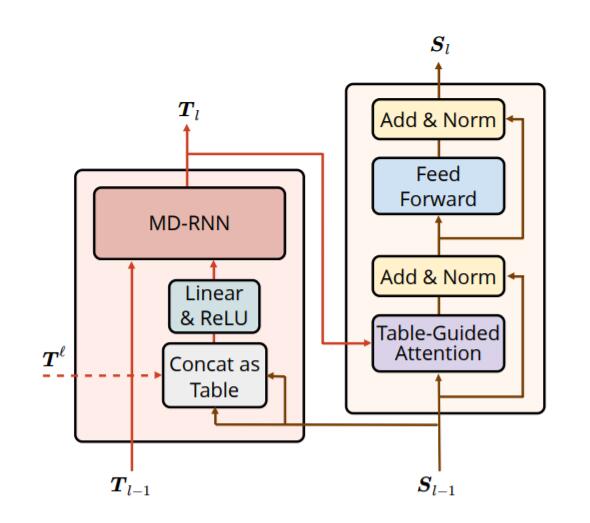
- 由Sequence Encoding和预训练模型的Attention Score一起得到最初的Table Encoding.
- Table Encoding内部用MD - RNN做表间和跨层的交互.
- Table信息通过Table - Guided Attention反作用于Sequence Encoder的训练.
总体来看设计还是挺精妙的.
Training and Evaluation
因为作者假定NER为序列标注问题, RE为填表问题, 所以直接拿Sequence的结果$\boldsymbol{S}_L$ 来标注NER, 填表$\boldsymbol{T}_L$ 的结果来标注RE:
$$
\begin{aligned}
P_{\theta}\left(\boldsymbol{Y}^{\mathrm{NER}}\right) &=\operatorname{softmax}\left(\operatorname{Linear}\left(\boldsymbol{S}_{L}\right)\right) \\
P_{\theta}\left(\boldsymbol{Y}^{\mathrm{RE}}\right) &=\operatorname{softmax}\left(\operatorname{Linear}\left(\boldsymbol{T}_{L}\right)\right)
\end{aligned}
$$
这二者都是分类问题, 直接用交叉熵优化:
$$
\begin{aligned}
\mathcal{L}^{\mathrm{NER}} &=\sum_{i \in[1, N]}-\log P_{\theta}\left(Y_{i}^{\mathrm{NER}}=y_{i}^{\mathrm{NER}}\right) \\
\mathcal{L}^{\mathrm{RE}} &=\sum_{i, j \in[1, N] ; i \neq j}-\log P_{\theta}\left(Y_{i, j}^{\mathrm{RE}}=y_{i, j}^{\mathrm{RE}}\right)
\end{aligned}
$$
最终目标就是联合优化二者, 即最小化$\mathcal{L}^{\text{NER}} + \mathcal{L}^{\text{RE}}$.
在推断时, 还是把NER和RE作为两个任务分别处理.
对于NER任务, 简单的有:
$$
\underset{e}{\operatorname{argmax}} P_{\theta}\left(Y_{i}^{\mathrm{NER}}=e\right)
$$
对于RE任务, 需要区分开关系所对应的Subject和Object. 对于NER抽取到的两实体的Span$\left(i^{b}, i^{e}\right), \left(j^{b}, j^{e}\right)$, 关系由下式得来:
$$
\underset{\vec{r}}{\operatorname{argmax}} \sum_{i \in\left[i^{b}, i^{e}\right], j \in\left[j^{b}, j^{e}\right]} P_{\theta}\left(Y_{i, j}^{\mathrm{RE}}=\overrightarrow{r}\right)+P_{\theta}\left(Y_{j, i}^{\mathrm{RE}}=\overleftarrow{r}\right)
$$
$\perp$ 代表不存在关系, 它是不存在方向的.
Experiments
详细的参数设置请参照原论文. BTW, 附录里面还有作者很多小想法和实验结果, 建议阅读.
作者采用了ACE04, ACE05, CoNLL04, ADE这几个数据集.
下文中, 作者所采用的指标为F1 Score, NER仅当实体类型和边界均匹配时才算正确, RE当实体边界和关系类型匹配时才算正确.
Comparison with Other Models
作者将本文方法与诸多模型做对比, 结果如下:

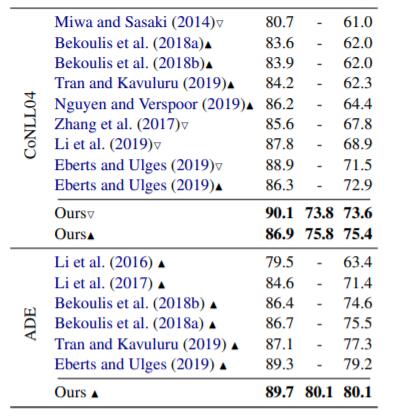
RE + 代表实体边界, 以及实体类型, 关系类型, 三者均匹配时才算正确, 比传统的RE任务要更加严格, 还包含了实体类型.
模型在上述数据集上均达到SOTA.
Comparison of Pre - trained Models
作者通过比较不同预训练之间的差距, 来间接凸显自己方法的有效性. 在ACE05上的结果如下:
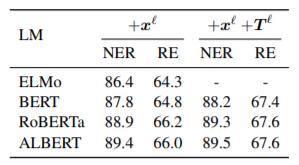
$+\boldsymbol{x}^\ell$ 代表使用了上下文相关的Word Embedding, $+\boldsymbol{T}^\ell$ 代表使用了Attention Weights.
即使是使用了不是真正上下文相关的ELMo, 性能依然能够与一些最好的模型媲美. 引入预训训练后, 性能进一步上涨, 在引入Attention Weights后涨幅比较大.
这证明了利用Attention Weight的重要性, 对NER和RE都有增益.
Ablation Study
Bidirectional Interaction
作者研究了NER和RE这两个任务之间的交互对性能的影响:
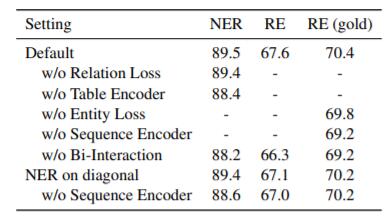
RE(gold) 代表在做RE时候直接使用Golden Entity.
结论如下:
- 不使用NER Loss或者不使用RE Loss, 都会降低性能, NER和RE彼此间确实存在关联, 且有相互促进作用.
- 不使用Table Encoder或不使用Sequence Encoder都会对性能产生负面影响, 如果切断两个Encoder之间的交互, 效果会更差.
- 如果直接把Table Representation的主对角线用来做NER任务, 也就是把NER和RE统一在一个空间中解决, 效果也不错, 但达不到作者的设置. 作者认为这是因为NER和RE仍然存在潜在差异, 不能直接用RE任务的Feature来做NER. 在该基础上, 继续去掉Sequence Encoder, 效果会变差, 这表明了Sequence信息对NER的作用.
Encoding Layers
作者探究了Encoder层数对性能的影响, ACE05上结果如下:
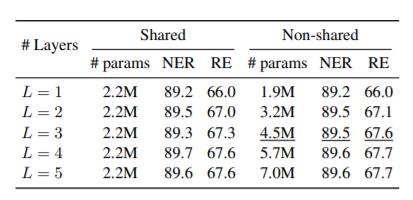
堆到3层的时候性能就没有明显提升了, 如果每层的参数共享, 层数越多越好.
Settings of MD - RNN
作者还对不同MD - RNN设定做了探究, 在ACE05上部分结果如下:

就如在前文中提到的, 四方向的效果并不比双向好太多. 且融入跨层信息后对RE提升比较大.
Attention Visualization
作者还模型做了Attention可视化:

相较于ALBERT下的Attention, 本文提出的Table - Guided Attention要更像人类的Ground Truth一些, 可视化一定程度上说明了改进的有效性.
Probing Intermediate States
在ACE05中作者挑了一个Case, 然后把训练好的Linear层放在每层Encoder后面检测结果:
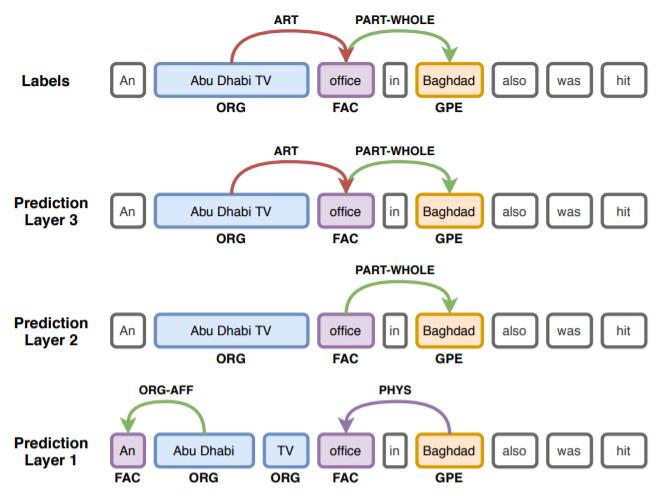
从下到上层数依次变深, 能看到模型逐渐对结果做修正, 作者认为更多地允许层间交互有助于捕捉困难实体和关系.
Probing在这里起作用的原因是作者引入了跨Encoder层信息.
Summary
在当时, 填表类的联合抽取模型已经有几年没有被提起, 此篇论文算是重新将填表式的方法抬上了桌面.
作者注意到了联合模型中存在的任务特征学习冲突问题, 并设计了一种两个独立Encoder的迭代式交互提升模型. 实验做的非常全面, 还用到了Probing等手段, 最后得到了”Two are better than One“的结论.
非常巧合的是, 本文同期与另一篇论述Pipeline模型不一定弱于Joint模型的文章A Frustratingly Easy Approach for Entity and Relation Extraction得到了相似的结论, 这篇文章打算下次更新, 算作三部曲中的第二部.

