本文前置知识:
End-to-end Structure-Aware Convolutional Networks for Knowledge Base Completion
本文是论文End-to-end Structure-Aware Convolutional Networks for Knowledge Base Completion的阅读笔记和个人理解.
Basic Idea
作者注意到ConvE中存在如下不足:
- ConvE中没有融入太多的结构信息(特指图结构信息和节点属性信息).
- ConvE没有像TransE一样保留平移的特性, 即$e_s + e_r \approx e_o$.
基于上述两点不足, 作者希望能够在ConvE架构下融入图中的结构信息, 并保留类似平移的特性.
作者观察到, ConvKB中存在类似保留平移特性的方法, 它与ConvE有几点不同:
- ConvKB只使用了1D卷积, 而ConvE使用了2D卷积.
- ConvKB使用了Stack, ConvE使用的是Reshape.
- 损失函数不同.
同时, ConvKB的作者也指出, 在特殊情况下ConvKB可以退化成TransE, 即能够保留平移特性. 受到ConvKB的启发, 作者提出了结构感知的Conv系列方法.
SACN
SACN(end-to-end Structure - Aware Convolutional Network)将融入结构信息的过程设计为Encoder - Decoder架构. 通过Encoder捕获图结构信息, 然后用Decoder从编码中解码出尾实体Embedding.
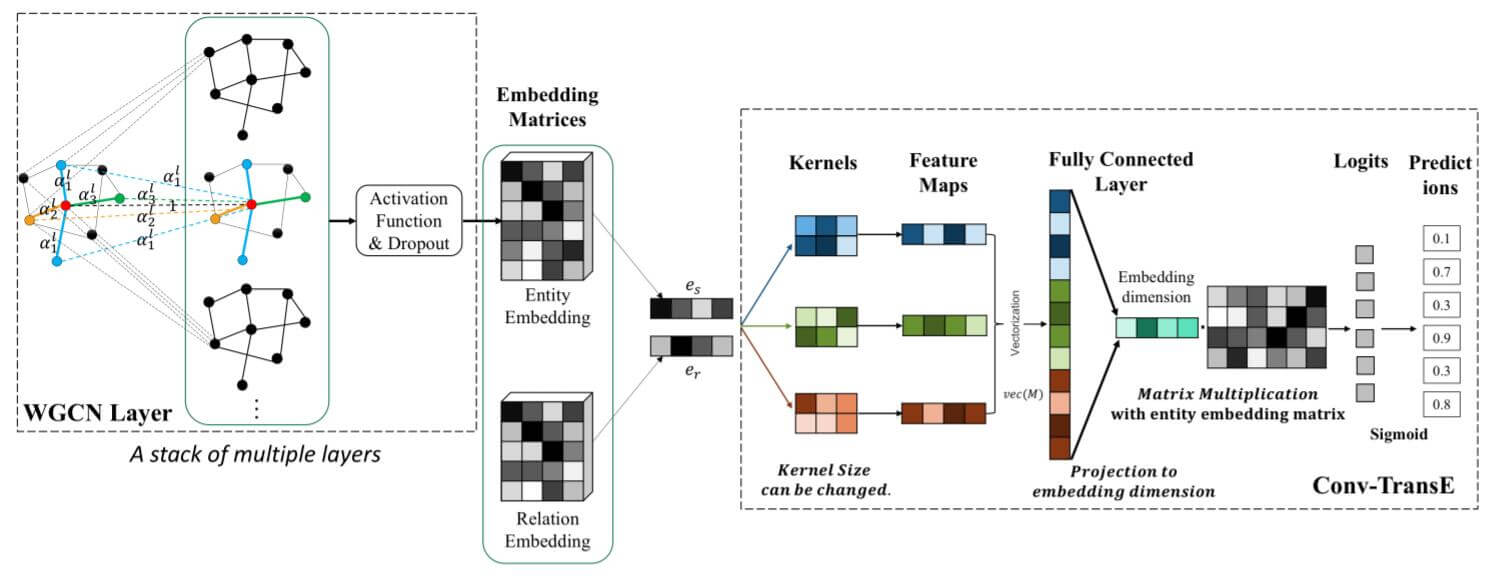
Weighted Graph Convolutional Layer
Weighted Graph Convolutional Network(WGCN)是GCN的一种扩展类型, 它将多关系图看做是多个单关系的子图. 因此对于每种不同的关系, WGCN都能决定子图中的节点以多少权重被集成, 即给予图结构多种不同的关系以不同的权重. 在SACN中, 它充当Encoder, 用于提取图结构信息.
其隐态更新方程如下:
$$
h_{i}^{l+1}=\sigma\left(\sum_{j \in \mathbf{N}_{\mathbf{i}}} \alpha_{t}^{l} g\left(h_{i}^{l}, h_{j}^{l}\right)\right)
$$
其中, $\alpha_t$ 为关系特化的权重. $T$ 为关系的总数, $t \in [1, T]$. $g$ 为聚合方式.
如下图所示, 红色的中心节点周围有4个相邻节点, 但只有3种不同的关系, 它们以3种不同的权重被聚合.
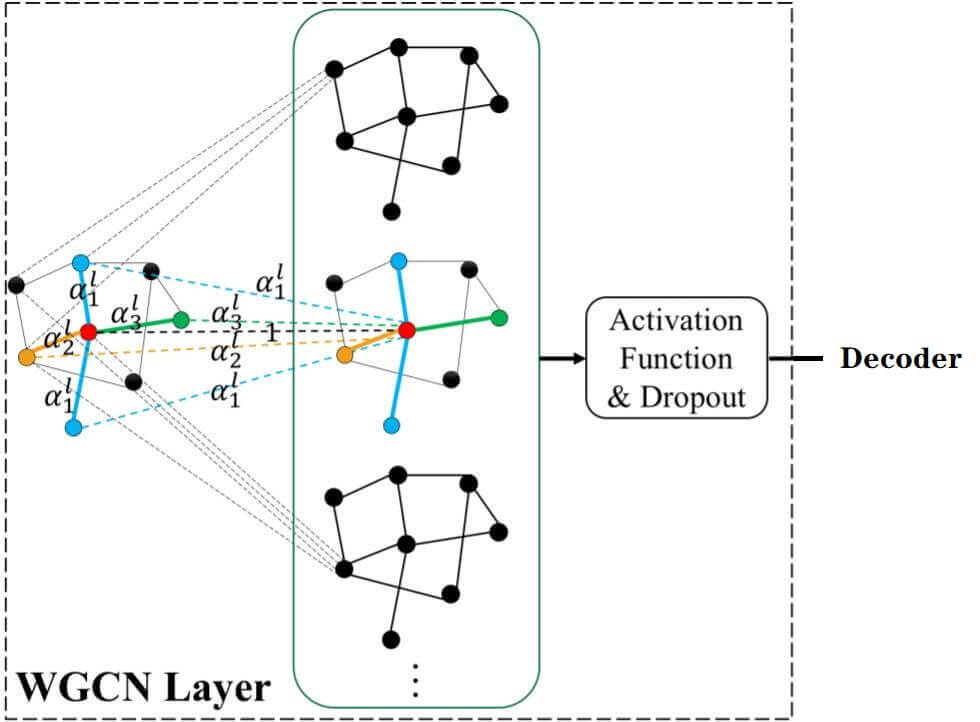
在WGCN中, 聚合方式采用了最简单的线性变换:
$$
g\left(h_{i}^{l}, h_{j}^{l}\right)=h_{j}^{l} W^{l}
$$
$W^l$ 为第$l$ 层的线性变换矩阵.
因为在考虑中心节点$i$ 的邻居节点$\mathbf{N_i}$ 时没有考虑节点自身到自身的闭环, 所以还是将闭环添加进来:
$$
h_{i}^{l+1}=\sigma\left(\sum_{j \in \mathbf{N}_{\mathbf{i}}} \alpha_{t}^{l} h_{j}^{l} W^{l}+h_{i}^{l} W^{l}\right)
$$
相当于给闭环分配了一种特殊的关系$\text{self-loop}$, 且权重$\alpha _{\text{self-loop}}=1$.
公式中的闭环是可以进行合并的:
$$
\begin{aligned}
h_{i}^{l+1}&=\sigma\left(\sum_{j \in \mathbf{N}_{\mathbf{i}}} \alpha_{t}^{l} h_{j}^{l} W^{l}+h_{i}^{l} W^{l}\right) \\
&=\sigma\left[\left(\sum_{i \in \mathbf{N}_i} \alpha_t^l h_j^l + h_i^l\right) W^l \right]
\end{aligned}
$$
在计算时, 将每种关系的邻接矩阵$A_t$ 分别乘以它们对应的权重$\alpha_t$, 视为第$l$ 层整张图的邻接矩阵$A^l$, 能一次性更新所有不同关系的节点隐态, 整个过程写成矩阵形式如下:
$$
\begin{aligned}
H^{l+1} &= \sigma \left[ \left( \sum_{t=1}^T \left(\alpha_t^l A_t \right) + I \right) H^l W^l \right] \\\
&=\sigma\left(A^{l} H^{l} W^{l}\right)
\end{aligned}
$$
计算流程如下图所示:
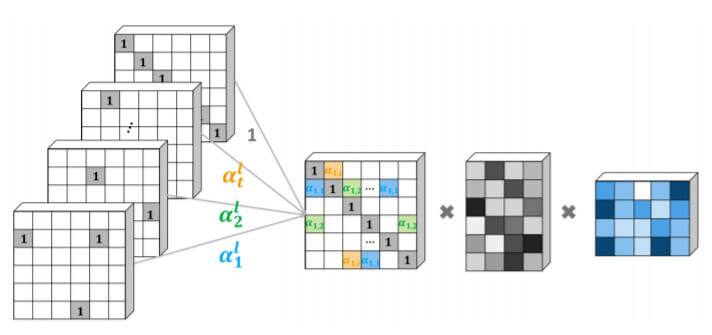
最左侧的一堆矩阵表示闭环的单位矩阵$I$ 和代表不同关系的邻接矩阵$A_t$, 第二个矩阵代表它们在不同关系$t$ 下与对应权重$\alpha_t$ 的加权和$A^l$. 第三个矩阵为$H^l$, 第四个为$W^l$.
但WGCN没有像经典GCN一样将度的信息集成进来.
Node Attributes
作者提到, 在当前KG中有一部分属性三元组, 即(entity, relation, attribute), 例如(Tom, people.person.gender, male).
这种属性三元组建模会带来两种潜在问题:
- 属性与一般节点不同, 它不能再延伸出其他的节点, 会导致属性特征非常稀疏.
- 由于其稀疏性, 属性特征中的0值可能会产生歧义, 可能是节点没有特殊的属性, 也可能是节点丢失了属性. 会影响KGE准确率.
如果需要减少过多的属性节点, 作者提出一种方法, 每一种属性将作为一个单独的属性节点.
这里有很大疑问, 作者的回复也比较模糊. 建议自行阅读原论文. 关于这块的吐槽在后面构建FB15k - 237 - Attr时我会详细说.
WGCN同时使用了图结构信息和属性信息, 这也就是”Structure Awared“的来源.
Conv - TransE
Conv - TransE在SACN中扮演Decoder的角色. 它能像TransE一样保留平移特性. 它仍然沿用ConvE的架构, 但它的核心点在于: 不进行Reshape.
作者认为正是ConvE中的Reshape操作将头实体嵌入$e_o$ 和关系嵌入$e_r$ 转化为2D向量才使得平移特性不能保存. ConvKB中的Stack操作却没有破坏原本的$e_o, e_r$形状.
因此, 从Encoder(WGCN) 中得到实体嵌入$e_o$后, 与关系嵌入$e_r$ 一起Stack起来, 不经过Reshape, 直接用宽度为2的2D卷积抽取得到Feature map.
WGCN只训练了Entity Embedding, Relation Embedding此时还是刚初始化的状态.
后面的流程和ConvE一样, 将Feature map打平, 再用投影层投回Embedding的维度, 和整个Embedding矩阵相乘得到Logits. 最后用Sigmoid得到概率, BCE计算损失:
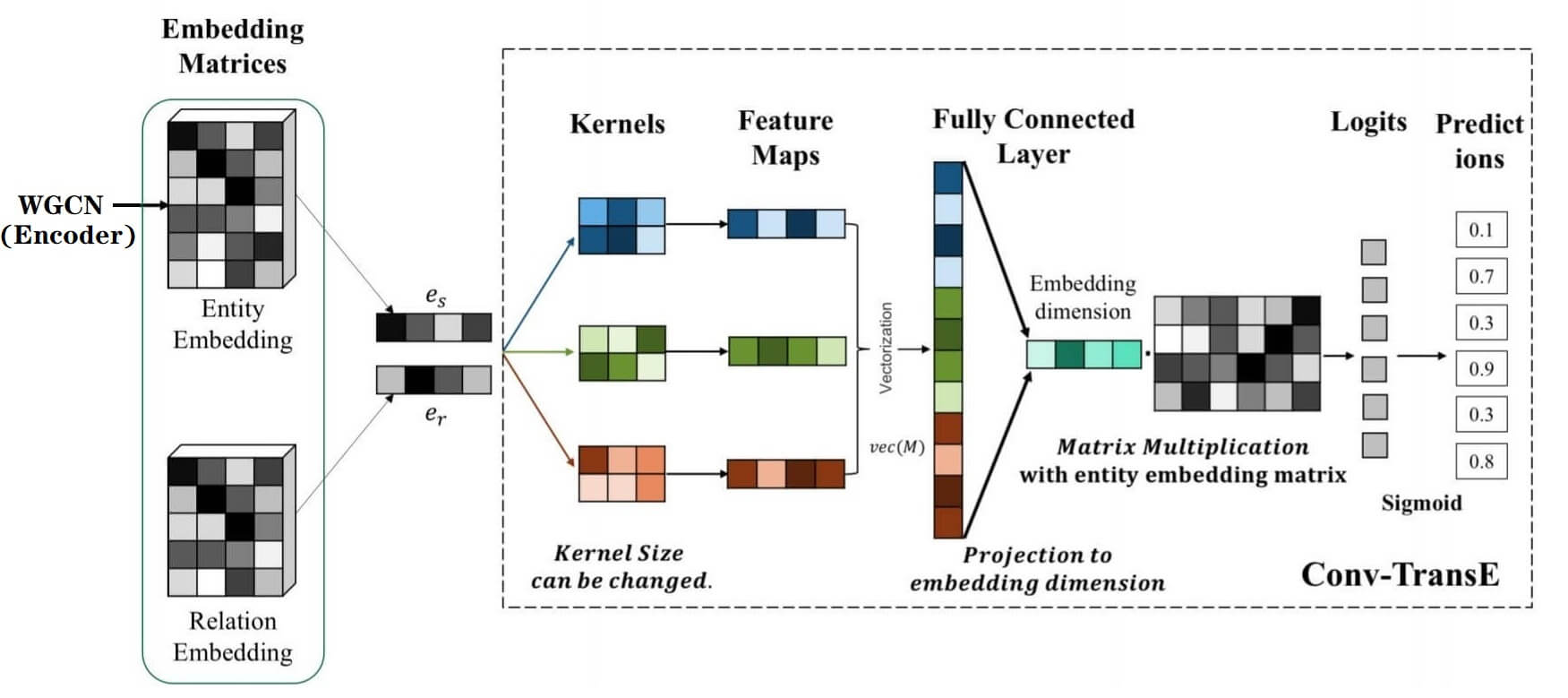
ConvKB采用的是宽度为1的2D卷积, 所以作者将ConvKB视为Conv - TransE的一种特殊情况.
卷积运算的数学描述如下:
$$
\begin{aligned}
m_{c}\left(e_{s}, e_{r}, n\right)&= \sum_{\tau=0}^{K-1} \omega_{c}(\tau, 0) \hat{e}_{s}(n+\tau)+\omega_{c}(\tau, 1) \hat{e}_{r}(n+\tau) \\
M_c(e_s, e_r) &= \left[ m_c(e_s, e_r, 0), \dots, m_c(e_s, e_r, F^L - 1)\right]
\end{aligned}
$$
其中$K$ 为卷积核宽度, $\omega_{c}$ 为卷积核权重.
卷积核能够分别对$e_s, e_r$ 加权, 并将二者相加, 作者认为这样保留了基于平移的性质.
我个人认为后面的投影层可能会破坏这种性质.
打分函数如下:
$$
\psi\left(e_{s}, e_{o}\right)=f\left(\operatorname{vec}\left(\mathbf{M}\left(e_{s}, e_{r}\right)\right) W\right) e_{o}
$$
其中$\mathbf{M}$ 为在WGCN上编码后的卷积操作, $\operatorname{vec}(\cdot)$ 为Flatten操作. $W$ 为投影层的投影矩阵, $f$ 为非线性激活函数. $e_o$ 为尾实体的Embedding.
与ConvE相同, 得到得分后再用对数几率函数得到概率:
$$
p\left(e_{s}, e_{r}, e_{o}\right)=\sigma\left(\psi\left(e_{s}, e_{o}\right)\right)
$$
得到概率后用BCE做损失函数优化.
SACN的打分函数整体形式与ConvE相同:

Experiments
详细的实验参数请参照原论文.
Dataset
除了两个Benchmark数据集FB15k - 237和WN18RR, 作者还利用实体的属性特征构建了一个新的数据集FB15k - 237 - Attr. 它是作者从FB24k抽取了FB15k - 237中的所有实体属性所构建的数据集. 它具有14541个节点, 203种属性, 484种关系. 共计78334个属性三元组, 这将近8w个三元组被作者全部并入训练集中.
花了很久看这里, 也不知道作者到底是如何具体构建的.
在实际的FB15k - 237 - Attr中, 作者直接将所有FB24k中同实体的属性三元组拿了过来. 但有些相同含义的三元组在FB15k - 237中是已经存在的, 这些已经存在的三元组没有被删除. 这样一来, 这些属性不单以”关系”的身份存在, 也以”属性”的身份存在, 而且在属性三元组中, 有些属性节点得到了合并, 但有些又没有, 感觉有点奇怪.
单纯从后续的实验结果来看, 使用该数据集是会涨点的.
作者将SACN在FB15k - 237和WN18RR上做了Link Prediction:
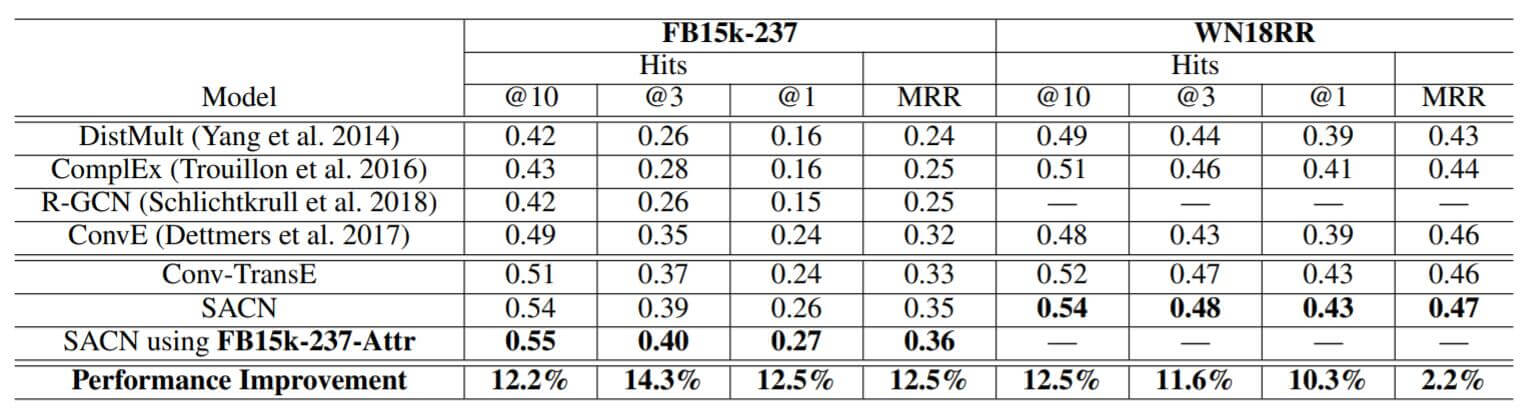
Conv - TransE相比较于ConvE有一定提升, 在引入WGCN后的SACN又有一定提升, 如果让SACN使用属性信息还会有一点点提升.
Convergence Analysis
作者分析了SACN + Attr(绿), SACN(红), Conv - TransE(黄)在Hits@1和MRR上的收敛性:
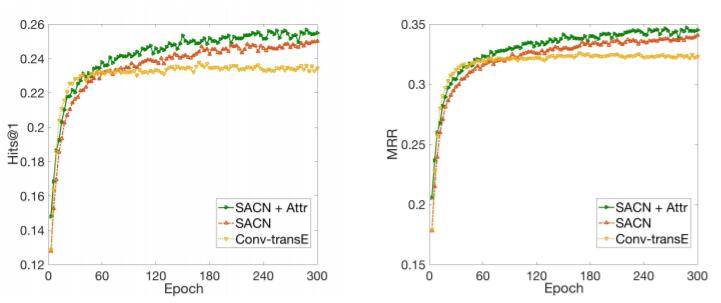
Conv - TransE在Epoch较少时性能是比SACN要好的, 随着轮数的增加, SACN性能反超了Conv - TransE.
而加入属性信息后, SACN性能得到了完全的提升.
Kernel Size Analysis
作者分析了不同卷积核大小对性能的影响:
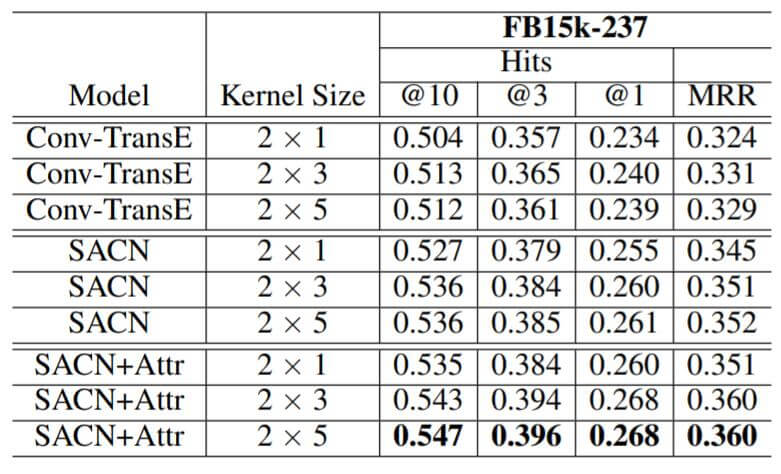
增大卷积核的大小会获得一点性能上的提升, 对于不同的数据集有不同的最优超参数设置.
Node Indegree Analysis
作者分析了节点入度对结果的影响:
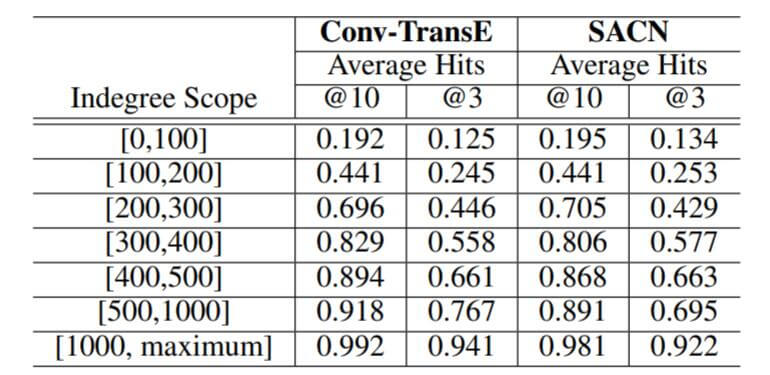
在度不够高时, SACN要略好于Conv - TransE, 在度比较大时, Conv - TransE会好于SACN. 作者解释为高入度导致SACN学到的邻居特征被平滑了.
Summary
SACN是一种基于Encoder - Decoder架构的卷积KGE方法, 保留了TransE基于平移的特性, 并集成了图结构和属性信息. WGCN也是一种GCN的扩展形式, 可以单独针对多关系作为基本的GNN组件存在.
WGCN抽取Entity Embedding的同时没有对Relation Embedding做更新, 或许可以利用图中的边对Relation Embedding增益, 例如尝试用Entity Embedding和Relation Embedding的联合训练.
关于属性节点的部分没太搞懂, 感觉比较模糊.

