本文前置知识:
- 图结构基础知识(数据结构相关内容, 自行查阅).
2021.04.06: 更新GraphSAGE的理解.
Introduction: Graph Neural Network
本文介绍的是GNN方面入门级别的知识, 其实这坑早就挖下了, 但是一直都没有机会补. 部分内容出自飞桨图神经网络7日打卡营, 训练营的切入的角度避开了复杂的数学推导, 方便GNN入门.
关于实现, 现在还没有统一的比较成熟的图学习框架, 无论是PyTorch还是TF, 都需要自己手动实现.
有两个图学习框架PyG 和DGL是大家用的比较多的, 但是都有一些问题, 目前来看PyG的人气比DGL要高得多. 还有百度飞桨的框架PGL, 感谢飞桨PGL在图学习开源上做出的贡献.
文中所涉及的所有论文和图片出处在结尾都会提供.
Graph and Graph Learning
诸如图的有向, 无向, 邻接矩阵, 矩阵的度之类的基本概念就不再赘述, 如果你对图结构本身还不太熟悉的话, 去重温一下数据结构就好.
在现实生活中, 图结构有多种很相关的实例. 例如分子结构, 交通流量, 社交网络, 知识图谱等… 非常多的复杂问题都能够被图所表示, 因为图本来就是一种表示能力极强的结构, 这使得许多利用简单结构不能被表示的问题得以表示. 也正是因为欧式数据和非欧数据在处理问题上的差异, 导致我们需要探索一种在非欧数据问题上生效的方法.
如果从图本身的角度来看, 单张图本身可以看做是茫茫众多图中的一个, 如果完成任务需要依赖于不同的图, 可以被称为是图级别任务,
如果从图结构的角度来看, 每张图中的节点和边都能够用作在不同的任务中. 节点或许可以代表问题中的某个实物, 边可以表示不同节点(实物)和节点之间的联系. 使用它们两个也就照应着节点级任务和边级别任务.
按照飞桨训练营中对图学习的划分, 图学习算法可以分为三大类:
- 图游走类算法(图嵌入算法): DeepWalk, Node2Vec等.
- 图神经网络算法: GCN, GAT, GraphLSTM等.
- 知识图谱嵌入算法: TransE, TransR, RotatE等.
现在主流的知识图谱嵌入和图嵌入有一些区别, 所以单独列了一类. 因为现在的Knowledge Embedding方法大多采用三元组的形式来获取嵌入表示. 当然也有结合图的算法, 例如R - GCN等.
图嵌入和图神经网络互有交集, 但图嵌入更侧重于只得到节点的低维表示, 而图神经网络侧重于将任务端到端的解决:
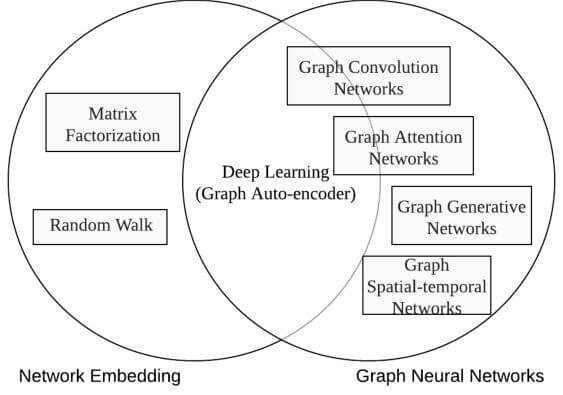
关于GNN发展过程中在频域, 空域上的一些内容在入门阶段很晦涩, 涉及到相当多的数学推导, 由于个人的基础不扎实在这里就不做误导了. 如果只是使用它, 不推荐关心这部分内容.
但如果是专门做GNN的研究, 这方面知识是非常有必要的. 并且需要掌握所涉及的推导过程.
给几个关于这方面的补充资料吧:
Graph Walking
图游走算法可以说是为图嵌入所服务的, 就好像Word Embedding对于NLP的地位一样, 为下游任务服务. 图嵌入可以得到一个节点在图中的表示(向量). 图游走就是通过某种游走算法将图转化为序列, 再使用类似NLP获取词嵌入的方式得到节点表示的方法.
Word2Vec
最早的游走思路是借鉴了NLP在处理词嵌入时所采用的Word2Vec, 在Word2Vec中, 中心词语义可以由周围邻近的词语义来”决定”, Skip - Gram便是一种根据中心词预测上下文来获取中心词嵌入表示的方法:
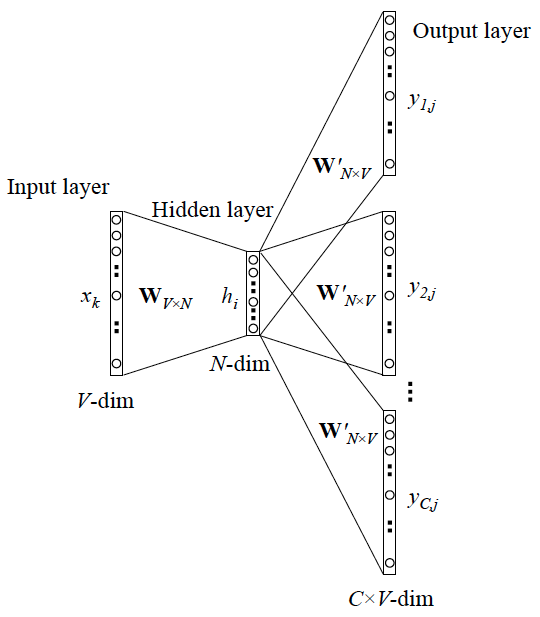
人们观察到, 社交网络中的用户行为经常会受到邻近用户的行为影响. 在图结构中, 只需要将中心思想变为中心节点含义由周围的节点决定, 本质上还是不变的. 所以就有可能将Word2Vec迁移到图领域用于获取节点嵌入表示.
DeepWalk
DeepWalk非常简单的在图中做随机游走, 即在当前节点的邻近节点(包括自身)随机游走, 当游走到最大长度时停止. 所以它是一个可以重复遍历的DFS.
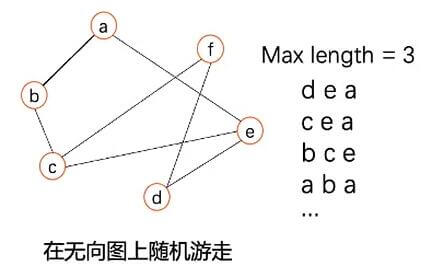
在这里定义一般的随机游走公式, 在节点$v$ 处游走到下一个节点$x$ 的概率为:
$$
{P}\left(c_{i}=x \mid c_{i-1}=v\right)=\left\{\begin{array}{cc}
\frac{\pi_{vx}}{Z}, & \text { if }(v, x) \in E \\
0, & \text { otherwise }
\end{array}\right.
$$
其中$Z$ 为归一化因子, $\pi_{vx}$ 是在被归一化之前算法得出的关于$v$ 游走到$x$ 的某个依据值.
对于DeepWalk来说, 只要与节点$v$ 相邻的节点概率是相等的, 所以有:
$$
P\left(c_{i}=x \mid c_{i-1}=v\right)=\left\{\begin{array}{cc}
\frac{1}{|N(v)|}, & \text { if }(v, x) \in E \\
0, & \text { otherwise }
\end{array}\right.
$$
拿到了这个图的遍历序列, 就能将它作为一个序列输入到Word2Vec中, 就得到了节点的表示.
Node2Vec
对于DeepWalk来说, 随机游走显得有些过于漫无目的, 没有偏好. 而且在DeepWalk中, 只考虑了使用DFS游走的方式. 而在数据结构中可知, 图的游走方式是有DFS和BFS两种的:
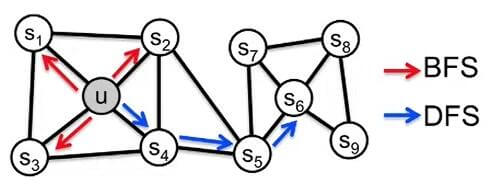
在Node2Vec中, 考虑了上述问题, 希望能够让游走的方式更加丰富一点. 只需要将图游走的一般公式做如下替换:
$$
\pi_{vx} =\alpha_{pq}(t, x) \cdot w_{vx}
$$
$v$为当前节点, $t$ 为上一个节点, $w_{vx}$为$v$ 和$x$ 之间的权值, 其中$\alpha_{pq}(t, x)$ 为:
$$
\alpha_{p q}(t, x)=\left\{\begin{array}{ll}
\frac{1}{p}, & \text { if } d_{t x}=0 \\
1, & \text { if } d_{t x}=1 \\
\frac{1}{q}, & \text { if } d_{t x}=2
\end{array}\right.
$$
$d_{tx}$ 代表节点$t$ 到$x$ 的距离, 即当前节点$v$ 的一阶邻居. 而$p, q$ 则是两个参数, 它们能控制如何游走:
- $p$ 能控制有多大的概率”回头”, 即从当前节点$v$ 重新回到前一节点$t$, 如下图$v\rightarrow t$).
- $q$ 控制游走策略倾向于DFS或是BFS:
- $q>1$ 时倾向于BFS, 如下图$v\rightarrow x_1$.
- $q<1$ 时倾向于DFS, 如下图$v\rightarrow x_2$.
- $p=q=1$ 时, $\pi_{vx}=w_{vx}$.
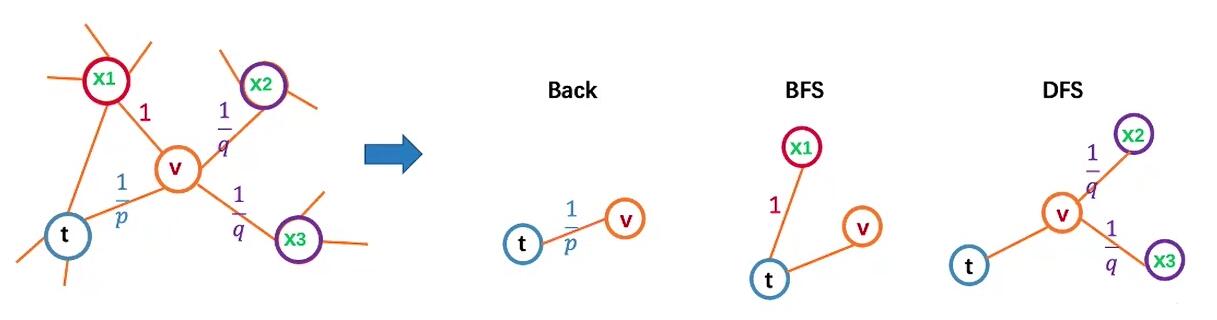
这样游走有如下好处:
- 结合了图的权重对游走的影响.
- 能够让模型自己学习如何游走合适(不是仅仅执行DFS, 也在某些时候BFS).
Graph Neural Network
Graph Convolutional Network
图卷积网络(Graph Convolutional Network, GCN)才彻彻底底的将卷积的概念从谱域扩展到了空域上. GCN将欧式结构上的卷积扩展到非欧结构上的卷积.
在CV中的卷积被定义为: 将某个像素点周围的像素以不同权重叠加起来. 那么扩展到图结构中这种非欧结构中, 对应的像素应该变为节点, 即将某个节点周围的邻居以不同权重叠加起来, 如下所示:

就像普通的CNN一样, GCN也是以若干层堆叠提取特征的方式发挥作用:
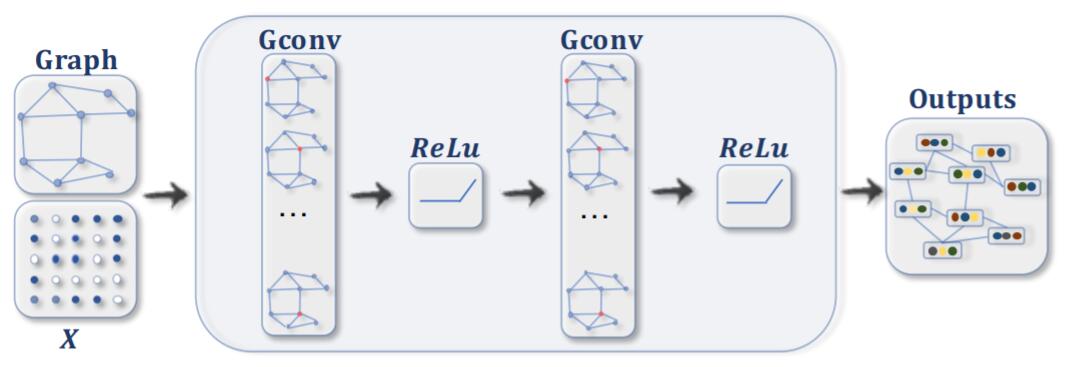
或是加上图池化与读出层做分类任务:
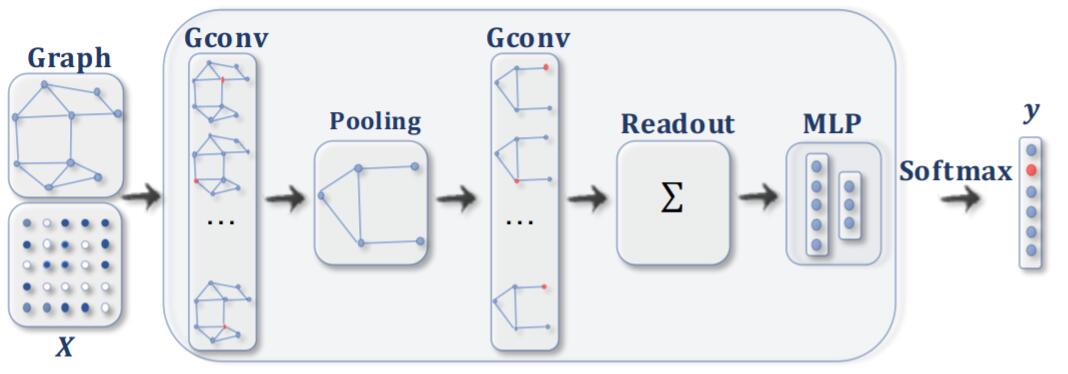
其中, 每一层GCN所对应节点隐态的更新方式为:
$$
H^{(l+1)}=\sigma(\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}H^{(l)}W^{(l)})
$$
其中$\hat{A}$ 为图的自邻接矩阵(有节点自身的闭环, 即$\tilde{A} = A + I$), $D$ 为度矩阵, $H^{(l)}$ 为第$l$ 层GCN的节点表示. $W^{(l)}$ 很好理解, 第$l$ 层的线性变换矩阵, 也就是”神经网络”(DNN).
以下图为例(图中有节点到自身的闭环):
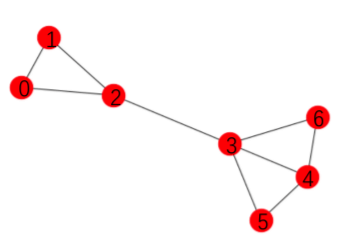
它所对应的邻接矩阵$A$, 度矩阵$D$ 分别为:
$$
\tilde{A}=\begin{bmatrix}\color{red}{1}&\color{red}{1}&\color{red}{1}&0&0&0&0\\\color{red}{1}&\color{red}{1}&\color{red}{1}&0&0&0&0\\\color{red}{1}&\color{red}{1}&\color{red}{1}&\color{red}{1}&0&0&0\\0&0&\color{red}{1}&\color{red}{1}&\color{red}{1}&\color{red}{1}&\color{red}{1}\\0&0&0&\color{red}{1}&\color{red}{1}&\color{red}{1}&\color{red}{1}\\0&0&0&\color{red}{1}&\color{red}{1}&\color{red}{1}&0\\0&0&0&\color{red}{1}&\color{red}{1}&0&\color{red}{1}\end{bmatrix}
\tilde{D}=\begin{bmatrix}\color{red}{3}&0&0&0&0&0&0\\0&\color{red}{3}&0&0&0&0&0\\0&0&\color{red}{4}&0&0&0&0\\0&0&0&\color{red}{5}&0&0&0\\0&0&0&0&\color{red}{4}&0&0\\0&0&0&0&0&\color{red}{3}&0\\0&0&0&0&0&0&\color{red}{3}\end{bmatrix}\
$$
其中所需要用到的$\tilde{D}^{-\frac{1}{2}}$ 为下矩阵:
$$
\tilde{D}^{-\frac{1}{2}}=\begin{bmatrix}\color{red}{\frac{1}{\sqrt{3}}}&0&0&0&0&0&0\\0&\color{red}{\frac{1}{\sqrt{3}}}&0&0&0&0&0\\0&0&\color{red}{\frac{1}{\sqrt{4}}}&0&0&0&0\\0&0&0&\color{red}{\frac{1}{\sqrt{5}}}&0&0&0\\0&0&0&0&\color{red}{\frac{1}{\sqrt{4}}}&0&0\\0&0&0&0&0&\color{red}{\frac{1}{\sqrt{3}}}&0\\0&0&0&0&0&0&\color{red}{\frac{1}{\sqrt{3}}}\end{bmatrix}
$$
为了方便理解更新方式, 我们先做如下方式的简化:
$$
\begin{aligned}
H^{(l+1)}&=\sigma(\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}H^{(l)}W^{(l)})\\\ &\Downarrow \\\ H^{(l+1)}&=\sigma(\tilde{A}H^{(l)}W^{(l)})
\end{aligned}
$$
即先不考虑度对更新的影响. $\tilde{A}H^{(l)}$ 的含义是:
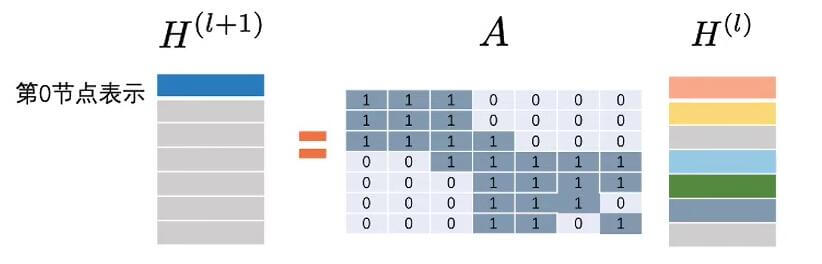
$l+1$ 层的第0节点表示是$l$ 层第0, 1, 2 节点表示的和. 这和CNN非常相似, 能根据邻接矩阵来判断邻居, 然后将邻居信息求和. 在计算下一层节点表示的过程中, 隐含着一种机制(或是框架), 消息传递:
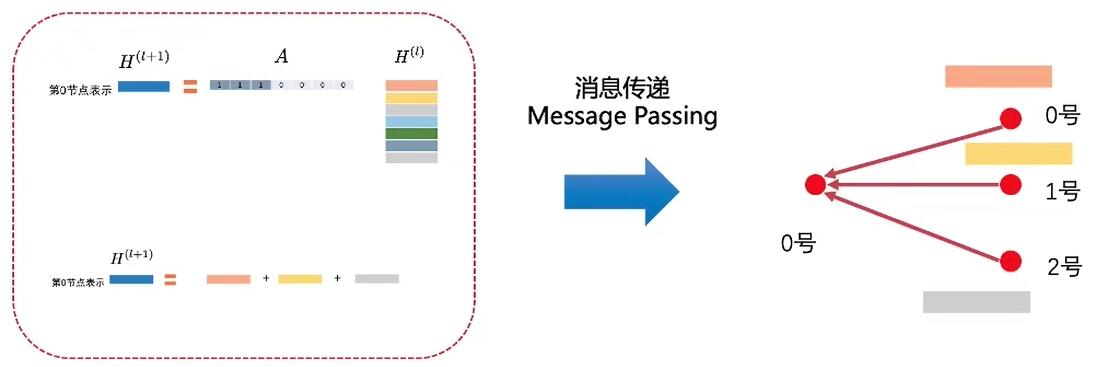
0号节点接收了来自0, 1, 2号节点的信息, 并更新了自己的信息. 消息传递的过程也就是这两步:
- 边上的源节点向目标节点发送信息.
- 目标节点对接收到的特征进行聚合.
既然已经能够完成特征更新的整个流程, 为什么要引入$\tilde{D}^{-\frac{1}{2}}$ 呢? 如果只使用邻接矩阵做加权, 周围人对你的评价可能并不是真实的:
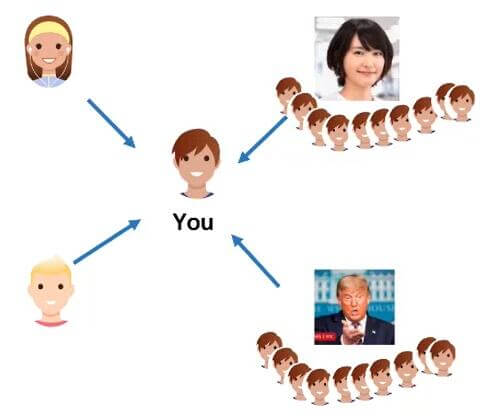
例如新垣结衣的周围的人非常多(度非常大), 她的特征可能会因为多人的评价而变得非常大, 从而对你的评价可能就不那么准确, 在训练时也容易导致梯度消失或梯度爆炸. 相反, 可能你的好友更加的了解你(度比较小), 对你的评价也更准确. 对所有节点一视同仁会导致度大的节点特征越来越大, 度小的节点越来越小.
因此, 我们可以使用度来衡量邻居信息的重要性, 这里的$\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}$ 在做的事情实际上是用度矩阵对$A$ 做了Renormalization:
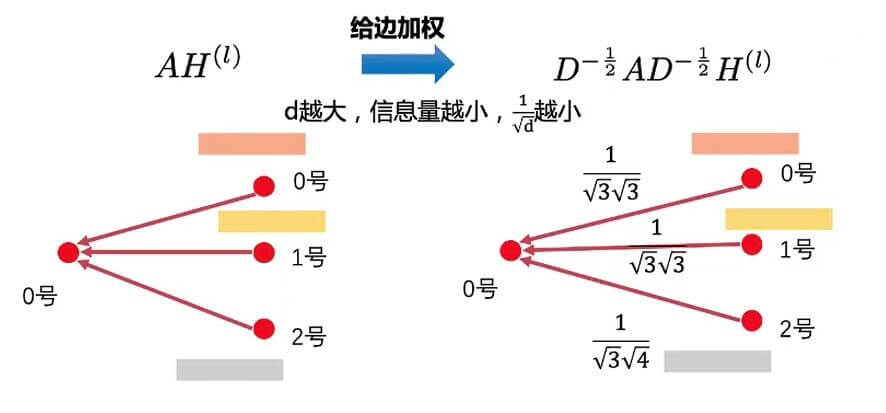
度$d$ 越大, 信息就越少, $\frac{1}{\sqrt{d}}$ 就越小.
这里采用Renormalization是有说法的, 想深入了解可以看GCN中的拉普拉斯矩阵如何归一化?.
之所以没有采用”对称归一化”这个说法, 是因为矩阵并没有真正的得到归一化, 原论文中的表述也是”Renormalization”.
下面来总结一下GCN的流程:
使用$\tilde{D}^{-\frac{1}{2}}\tilde{A}\tilde{D}^{-\frac{1}{2}}$ 进行节点之间的特征传递:
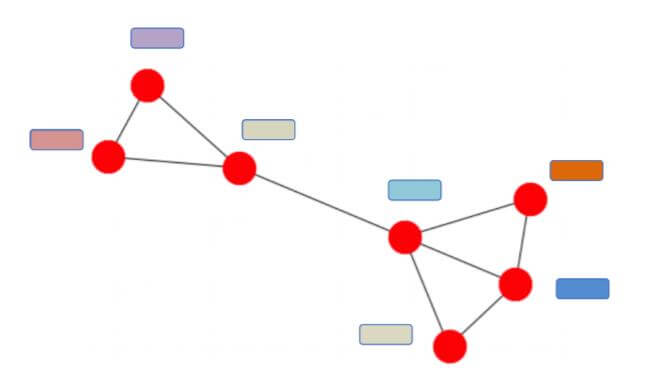
对每一个节点过一层DNN:
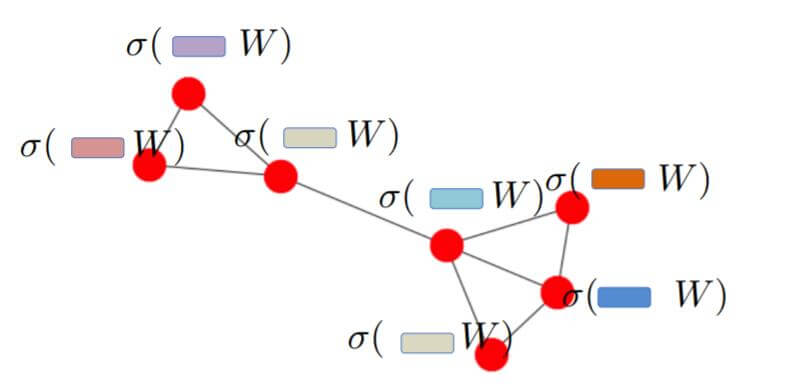
重复上面两步多次, 实现多层GCN, 并能获得每个节点的表示:
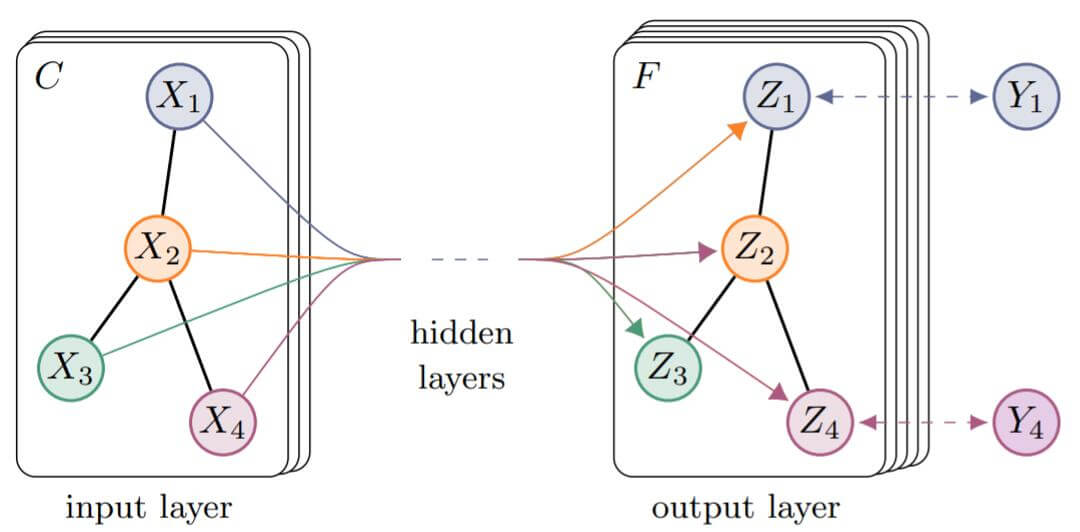
根据取得的节点表示$H^{(l)}$将其用于下游任务:
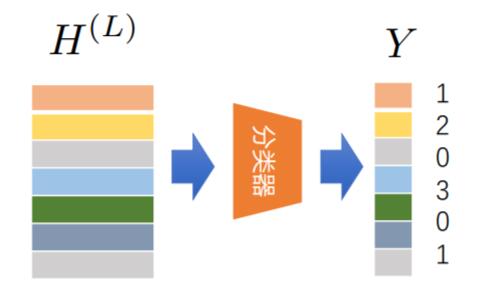
Graph Attention Network
在GCN中的边权重是通过度来控制的, 这种度量仅与度有关, 而且不可学习权重的分配方式.
在深度学习背景下, 我们更希望能够模型能够自己学习如何分配权重. 在深度学习中, 关于学习权重分配的分配方式, 人们很自然而然的就想到了Attention, 它也确实非常适合去做这件事情. 图注意力网络(Graph Attention Network, GAT)应运而生.
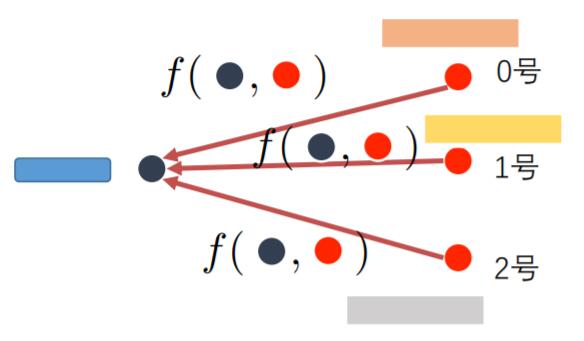
GAT通过对调整当前节点$i$ 对其他节点$j$ 的权重来调整, 在这里只考虑节点$i$ 的一阶邻居 $j \in \mathcal{N}_{i}$.
$$
e_{i j}=a\left(\mathbf{W} \vec{h}_{i}, \mathbf{W} \vec{h}_{j}\right)
$$
GAT中的Attention计算方式如下:
$$
\displaylines{
\alpha_{i j}=\operatorname{softmax}_{j}\left(e_{i j}\right)=\frac{\exp \left(e_{i j}\right)}{\sum_{k \in \mathcal{N}_{i}} \exp \left(e_{i k}\right)}
\\\ \Downarrow \\
\alpha_{i j}=\frac{\exp \left(\operatorname{LeakyReLU}\left(\overrightarrow{\mathbf{a}}^{T}\left[\mathbf{W} \vec{h}_{i} | \mathbf{W} \vec{h}_{j}\right]\right)\right)}{\sum_{k \in \mathcal{N}_{i}} \exp \left(\text { LeakyReLU }\left(\overrightarrow{\mathbf{a}}^{T}\left[\mathbf{W} \vec{h}_{i} | \mathbf{W} \vec{h}_{k}\right]\right)\right)}
}
$$
其中$\overrightarrow{\mathbf{a}}$ 是一个权重向量, 也可以被视作是一个单层神经网络, $\mathbf{W}$ 为权重矩阵, 能够学习到输入特征$\overrightarrow{h}$ 中更高级的特征. GAT计算各节点的高阶特征, 后计算各节点对当前节点的重要程度, 并经过LeakyReLU激活, 最后用Softmax做归一化, 求得Attention权重:
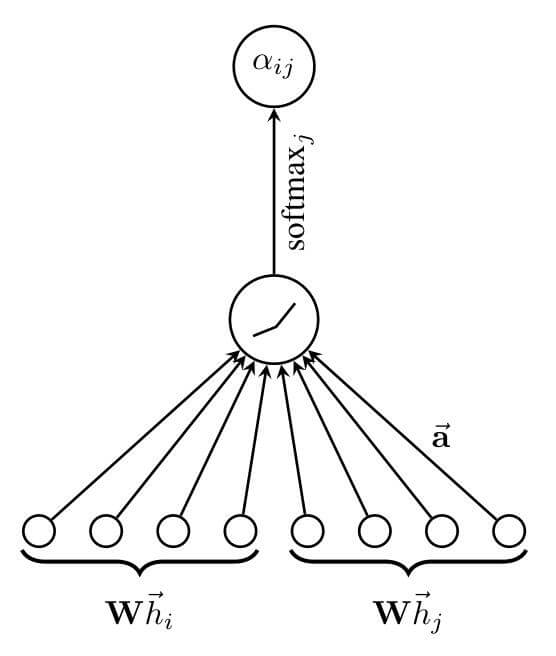
对特征的聚合方式如下:
$$
\vec{h}_{i}^{\prime}=\sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j} \mathbf{W} \vec{h}_{j}\right)
$$
$\sigma$ 是非线性的激活函数.
与Transformer一样, GAT也支持多头特征聚合:
$$
\vec{h}_{i}^{\prime}=\operatorname{\lVert}\limits_{k=1}^{K} \sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j}^{k} \mathbf{W}^{k} \vec{h}_{j}\right)
$$
其中$||$ 代表Concatenation. 即将多个头的特征Concat起来. 当然也可以采用求平均的方式来适应不同的场景:
$$
\vec{h}_{i}^{\prime}=\sigma\left(\frac{1}{K} \sum_{k=1}^{K} \sum_{j \in \mathcal{N}_{i}} \alpha_{i j}^{k} \mathbf{W}^{k} \vec{h}_{j}\right)
$$
GAT总体来说如下所示:
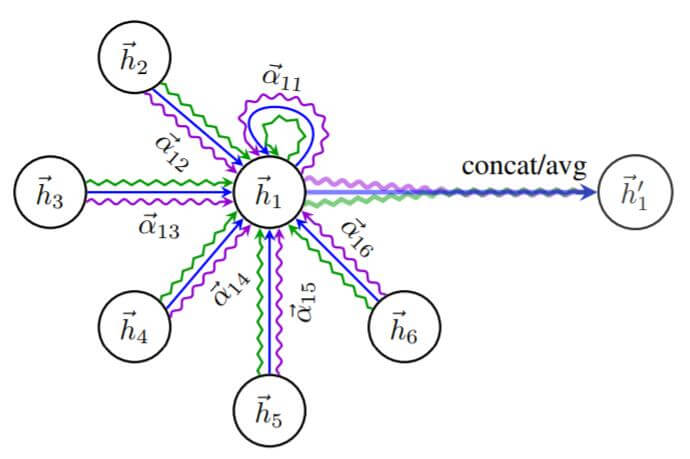
图中三种颜色的线代表有三个头, 学习到了不同的权重分配方式, 最后再通过某种聚合方式聚合获得$\overrightarrow{h_1^\prime}$.
因此, GAT不但将权重调整为与两个节点都相关的函数, 而且还是可学习的, 它同样遵守消息传递框架.
Message Passing Neural Network
消息传递网络(Message Passing Neural Network, MPNN)并非是某种具体的图神经网络, 而是对图神经网络更新权重方式的一种范式或是一种框架. 我在前面介绍GCN, GAT时曾多次提到这个词, 因为它们都是基于邻居聚合的模型, 都属于Spatial GNN, 大多数的空域GNN都是可以被消息传递网络实现的.
基于消息传递的 Graph Neural Network的通用公式如下:
$$
h_{l}^{(t)}(v)=\color{green}{f}\left(h_{l}^{(t-1)}, \color{red}{\mathcal{F}}\left\{\color{blue}{h_{l}^{(t-1)}(u) \mid u \in N(v)}\right\}\right)
$$
其中$h_{l}^{(t-1)}(u)$ 代表邻居的消息发送, $\mathcal{F}$ 代表聚合函数, 可以是Max, Mean, Sum等, $f$ 对应神经网络, 可以是MLP或者其他结构. 在GCN中, $\mathcal{F}$ 是基于度的加权求和, GAT中是基于Attention的加权求和.
Graph Sampling
因为节点和节点间存在依存关系, 并不像欧式数据那样可以采用MiniBatch的方法训练, 所以在大规模图中, 一般没有办法将算法直接应用于整张图, 例如GCN, 每次更新需要对所有节点依次聚合更新. 故需要一种能够从图中采样, 获取有效子图的方法, 在子图上应用我们前面说过的算法, 这种方法就是图采样.
但子图采样并不是随机采样, 我们最起码要保证采样完后的图是连通的:
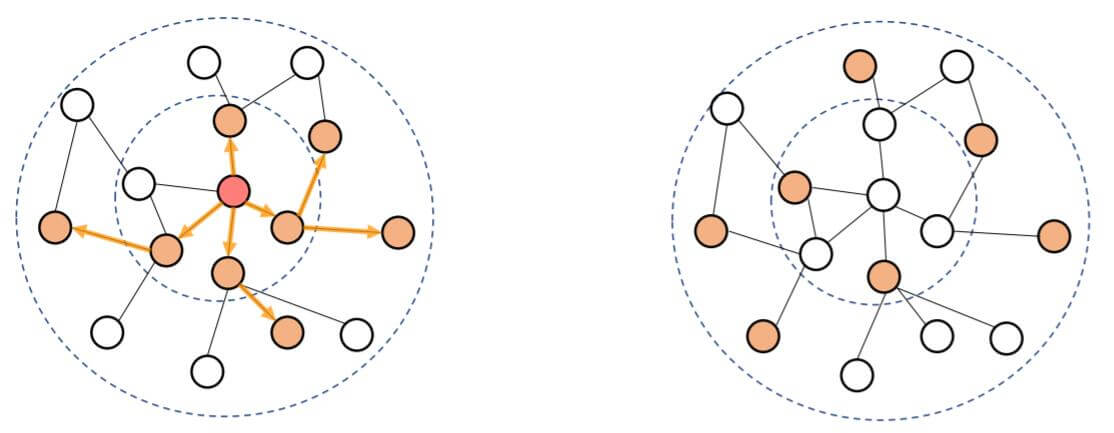
GraphSAGE
Graph SAmple & aggreGatE, GraphSAGE 是最简单的图采样算法. 它与GCN其实差别不大. 它分为邻居采样, 邻居聚合, 节点预测三个步骤.
假设有下面这么一张图, 我们需要求出0号节点的表示, 所以需要从0号节点开始采样:
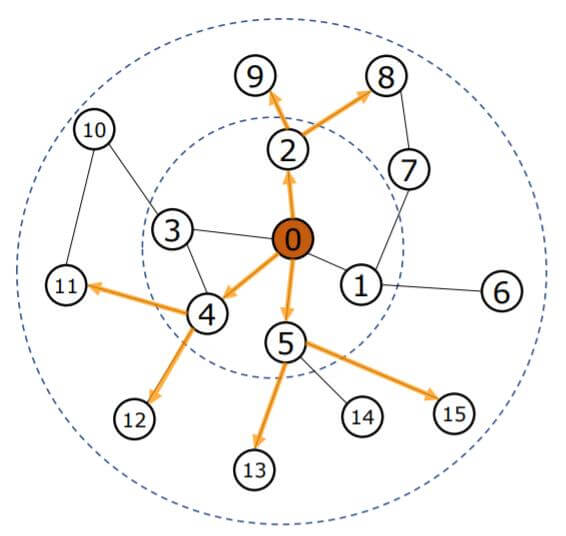
我们从内至外地采样0号节点的第N阶邻居, 假设一阶邻居随机采样到了2, 4, 5号节点, 然后采样二阶邻居8, 9, 11, 12, 13, 15:
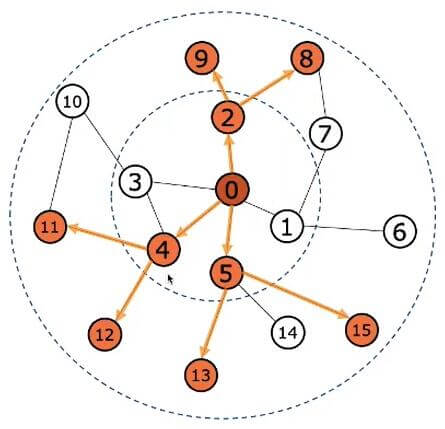
这样就抽出了一张子图, 然后可以由外至内地邻居聚合更新0号节点的表示:
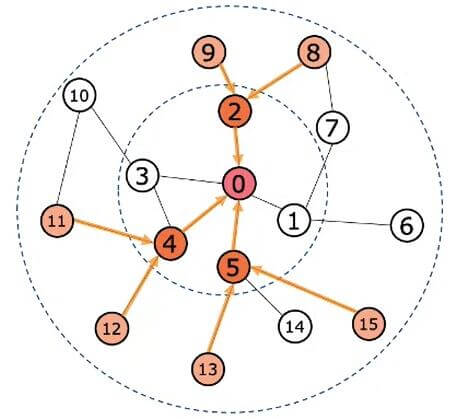
最后就可以通过采样获得的子图来做节点预测了.
邻居采样有两个优点:
- 极大减少了训练计算量.
- 在推断时允许新的节点的加入, 增强了泛化能力.
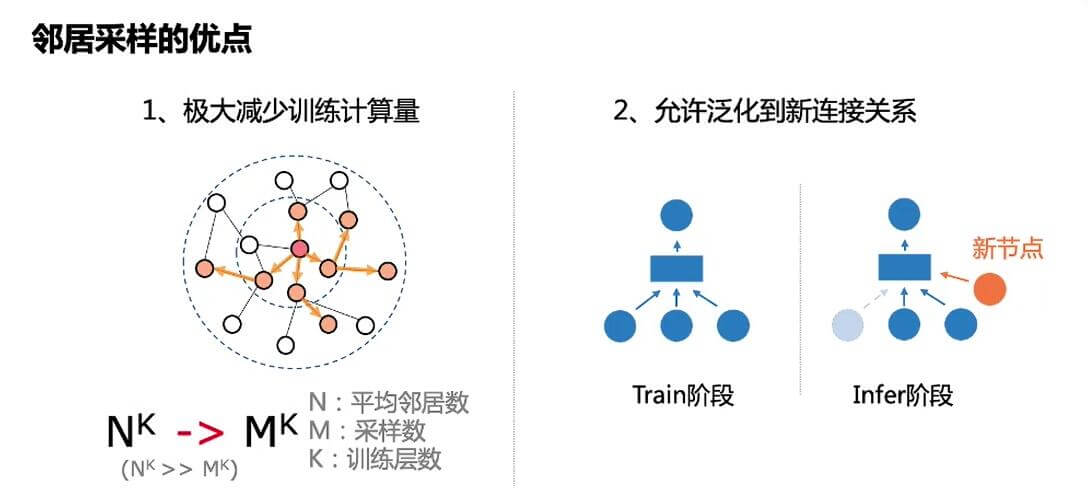
因为做了邻居采样, 所以更新未知节点的表示时不需要使用整张图的节点信息, 而是只使用由新加入节点后采样的子图节点信息, 所以说允许泛化到新的节点, 也就是所谓的Inductive能力.
关于GraphSAGE在Inductive上的能力讨论可以看这里, 我个人是比较赞同答主的说法. 算法能否Inductive和Transductive仅取决于节点输入是否是One Hot, 以及在更新节点表示时是否只依赖于局部子图.
PinSAGE
仍然是之前的那副图, 我们希望能够更新0号节点的表示. PinSAGE通过多次随机游走, 按照路径中节点出现的频率, 将这些节点作为邻居. 假设PinSAGE已经做出了四次随机游走:
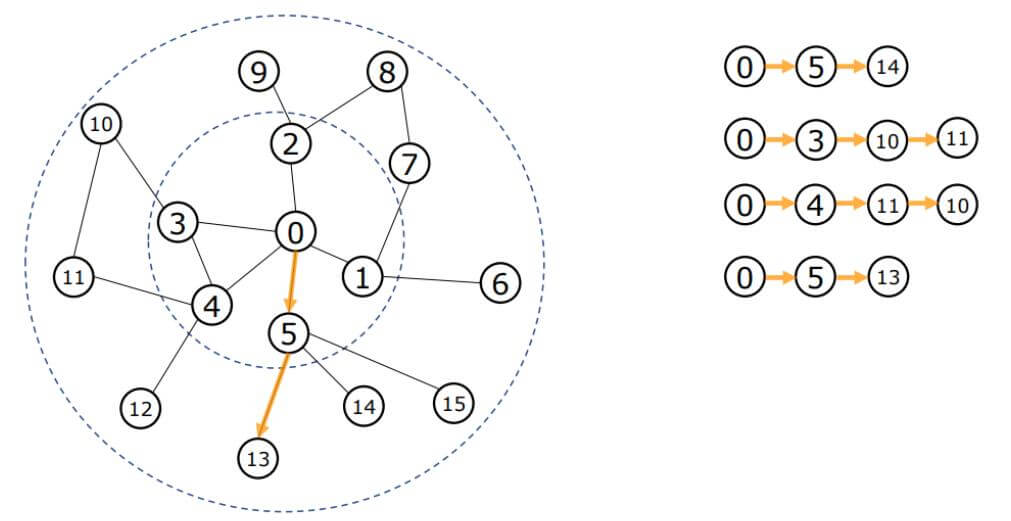
根据四次游走中节点出现的频率排序, 5, 10, 11这三个节点频率较高, 让它们作为0号节点的虚拟邻居:
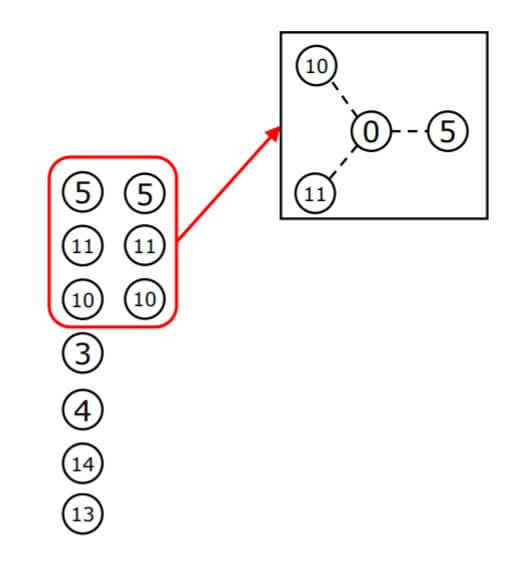
所以说, PinSAGE所采样得到的子图不一定选取了真实的邻居节点, 这样做使得节点能够快速的获取到高阶邻居的信息, 有点类似于ResNet中的Residual Connection的作用, 避免了聚合过程中由于距离过远而损失信息的缺点.
Neighborhood Aggregation
邻居聚合是在图采样之后做的操作, 不同的聚合方式可以达到不同效果. 经典的聚合函数有:

评估聚合表达能力的指标是单射, 单射能保证对聚合以后的结果可区分:

对于不同的子图, SUM也保留了单射能力:
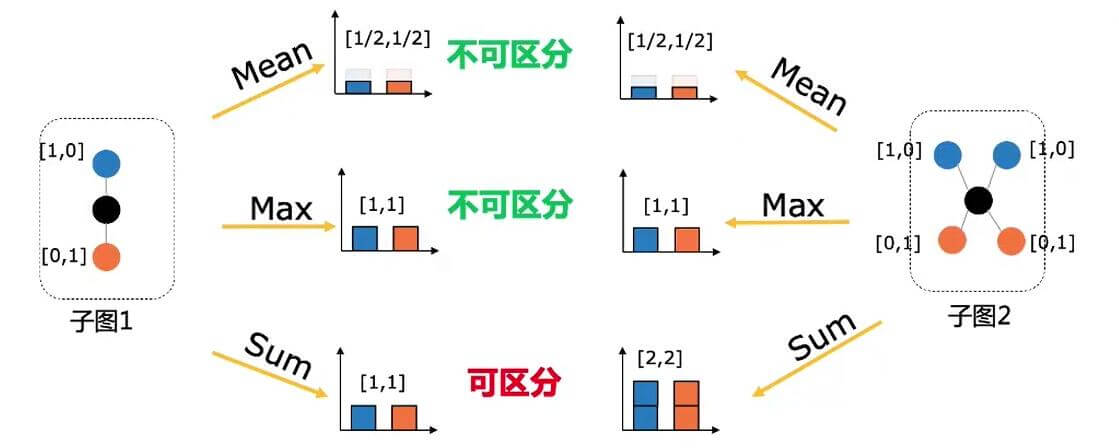
因此, 就有基于单射的GIN(Graph Isomorphism Net)模型:
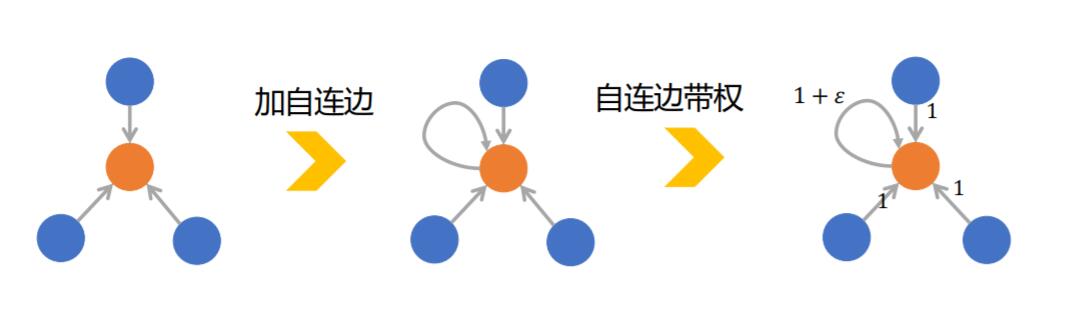
它的聚合方式就是具有单射能力的SUM, 但是为了区分中心节点与邻居, 特意加上了$\mathcal{E}$ :
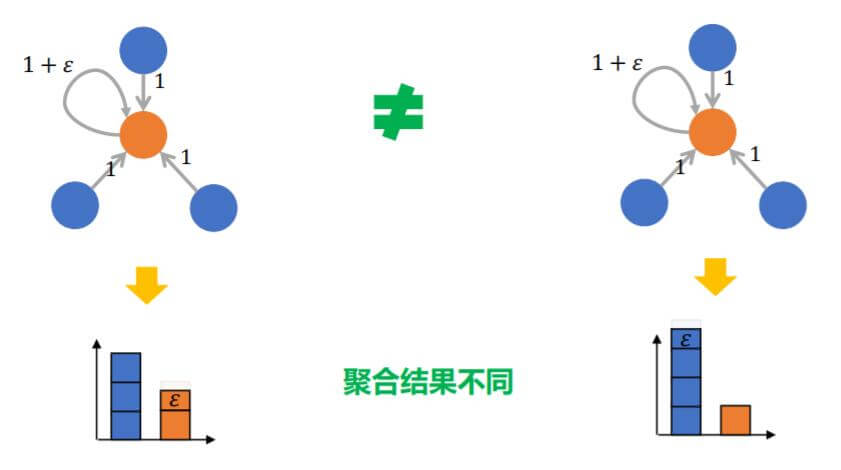
当然, GCN, GAT这类的聚合函数都是相较于经典聚合函数更为复杂的.
Recommended
涉及到的原论文和图片出处:
- DeepWalk: DeepWalk: online learning of social representations
- Node2Vec: node2vec: Scalable Feature Learning for Networks
- GCN: Semi-Supervised Classification with Graph Convolutional Networks
- GAT: Graph Attention Networks
- MPNN: Neural Message Passing for Quantum Chemistry
- GraphSAGE: Inductive Representation Learning on Large Graphs
- PinSAGE: Graph Convolutional Neural Networks for Web-Scale Recommender Systems
- GIN: HOW POWERFUL ARE GRAPH NEURAL NETWORKS?
- 综述类论文: A Comprehensive Survey on Graph Neural Networks
除去文中提到的资料, 其他涉及到的参考资料:
- GNN详解, GCN详解, GraphSAGE & PinSAGE详解
- CS224W: Machine Learning with Graphs
- 台大李宏毅助教讲解GNN图神经网络
- 图神经网络7日打卡营
- 深入浅出GCN、GAT、GraphSage,MPNN等图神经网络模型【贪心学院】
- GNN综述——从入门到入门
- 图卷积神经网络笔记——第三章:空域图卷积介绍(1)
- GCN—图卷积神经网络理解
PyTorch代码:

