ConvE: Convolutional 2D Knowledge Graph Embeddings

本文前置知识:

• CNN

本文是论文Convolutional 2D Knowledge Graph Embeddings的阅读笔记和个人理解. 与之前在AcrE中提到的ConvE不同, 本文重新对整篇论文进行叙述, 而非仅介绍论文中建模的部分.

Basic Idea

其实ConvE的出发点非常的简单, 就是之前的模型不够深, 有些简单. 因为之前使用的模型大多数采用矩阵映射, 内积等方式, 可能简单的模型能够处理小规模的KG, 想要提升性能就只能通过增大Embedding Dimension. 它们在大规模KG上不一定能获得良好的效果. 由于深度学习的兴起, 作者尝试将卷积引入到KGE领域, 使它能够在保证深度和模型复杂度的情况下能够处理大规模KG.

ConvE

ConvE其实就是将CNN移植到了KGE领域, CNN能在不引入过多参数的情况下, 高效而简单的提供多次交互.

1D Convolution vs 2D Convolution

作者指出, 相较于1维卷积, 2维卷积有更强的表达能力(其实从直觉来说也是这样).

在做1维卷积时, 卷积核最多只能与左侧或右侧离得比较近的元素交互:
$$
\left(\begin{array}{lll}
\left.\left[\begin{array}{lll}
a & a & a
\end{array}\right] ;\left[\begin{array}{lll}
b & b & b
\end{array}\right]\right)=\left[\begin{array}{llllll}
a & a & a & b & b & b
\end{array}\right]
\end{array}\right.
$$
但2维卷积不一样, 除了能够与邻近的左右元素交互, 还能与上下元素进行交互:
$$
\left(\left[\begin{array}{lll}
a & a & a \\
a & a & a
\end{array}\right] ;\left[\begin{array}{lll}
b & b & b \\
b & b & b
\end{array}\right]\right)=\left[\begin{array}{lll}
a & a & a \\
a & a & a \\
b & b & b \\
b & b & b
\end{array}\right]
$$
如果两种元素代表的意义不同, 那么交换它们的拼接方式还能进一步的提升交互次数:
$$
\left[\begin{array}{lll}
a & a & a \\
b & b & b \\
a & a & a \\
b & b & b
\end{array}\right]
$$
由于交换了Concat方式, a和b交错, 能够实现更多次交互. 所以作者认为, 2D卷积的表达能力比1D卷积要强, 因此不是单纯在1D的Embedding数据上做卷积, 而是尝试扩展到2D上做卷积.

在InteractE中, 使用了交错程度更大的棋盘式布局, 进一步提升了交互次数.

ConvE Architecture

我们先看ConvE的整体流程的概括:

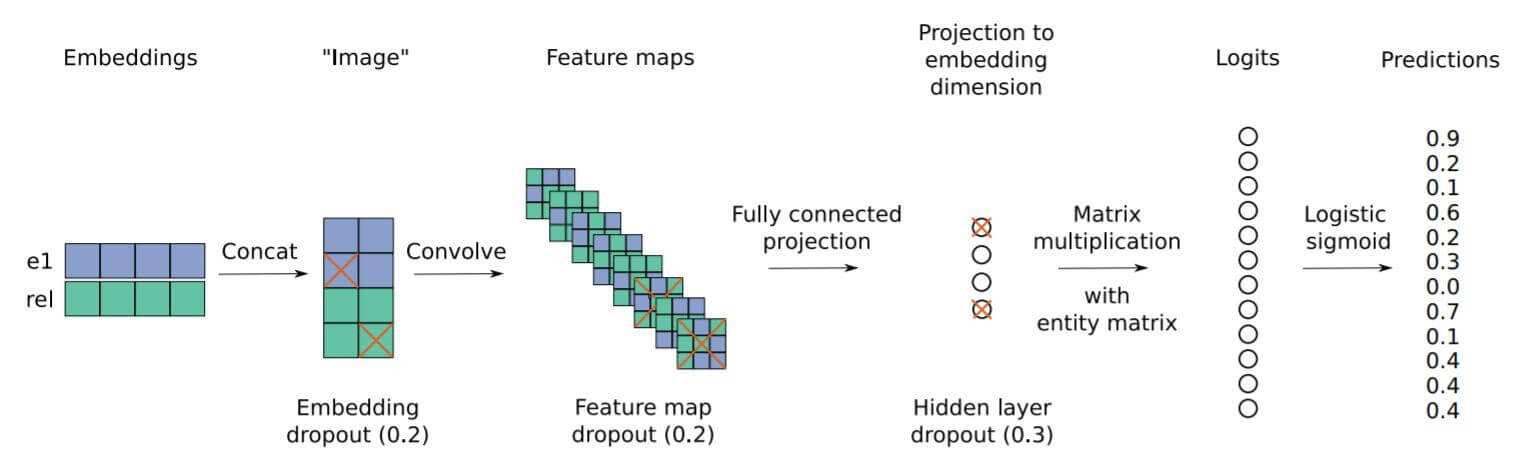
然后再给出ConvE的打分函数:
$$
\psi_{r}\left(\mathbf{e}_{s}, \mathbf{e}_{o}\right)=f\left(\operatorname{vec}\left(f\left(\left[\overline{\mathbf{e}_{s}} ; \overline{\mathbf{r}_{r}}\right] \ast \omega\right)\right) \mathbf{W}\right) \mathbf{e}_{o}
$$
其中$\mathbf{e}_{s}, \mathbf{e}_{o}$ 分别代表头实体和尾实体的Embedding, $\overline{\mathbf{e}_{s}}, \overline{\mathbf{r}_{r}}$ 分别代表Reshape后的头实体和关系向量. $\omega$代表卷积核, $\mathbf{W}$ 代表投影矩阵.

接下来对ConvE的打分函数进行讲解, 请结合概括图来看. ConvE先通过Embedding的方式分别获得头实体表示$\mathbf{e}_{s}$ 和关系表示$\mathbf{r}_{r}$. 将头实体和关系表示先Concat起来, 然后将其Reshape到某一种尺寸, 此时头实体和关系的表示记为$\left[\overline{\mathbf{e}_{s}} ; \overline{\mathbf{r}_{r}}\right]$. 接着利用卷积抽取Reshape后的二维向量, 也就是对头实体和关系进行交互. 利用卷积抽取完信息后, 将所有的特征打平成一个一维向量, 通过投影矩阵$\mathbf{W}$ 投影到隐空间中, 然后与为尾实体表示$\mathbf{e}_{o}$ 做内积, 获得相似度, 即Logits. 这种方式通过内积来比较所获向量与尾实体的相似度, 越相似得分越高.

然后将Logits经过$\sigma$ 函数, 得到每个实体的概率:
$$
p=\sigma(\psi_{r}\left(\mathbf{e}_{s}, \mathbf{e}_{o}\right))
$$
优化时的损失函数采用BCE:
$$
\mathcal{L}(p, t)=-\frac{1}{N} \sum_{i}\left(t_{i} \cdot \log \left(p_{i}\right)+\left(1-t_{i}\right) \cdot \log \left(1-p_{i}\right)\right)
$$
$t$ 是尾实体的独热编码向量. 除此外还加入了Dropout, BatchNorm, 标签平滑等防止过拟合的手段.

这个损失函数很有说法, 因为在ConvE提取过Feature后, 能获得对所有实体相关的Logits, 这样就能对所有的尾实体同时打分, 而不用考虑采样的问题. 在原文中这种打分方式被称为1 - N Scoring.

这种方式能极大地加快Evaluation的速度, 因为负采样只能对单一的三元组打分, 而这种方式能同时对所有的尾实体同时打分. 作者还测试了不对所有实体同时打分的情况, 例如只对10%的实体打分, 这种情况记为1 - 0.1 N Scoring, 虽然在正向传播和反向传播的速度减少了25%, 但训练速度慢了许多.

作者还指出, 这种思想能够应用于所有的1 - 1 Scoring Model.

Experiments

WN18RR

作者指出, 最常用的几个数据集例如FB15k, WN18都存在大量的互逆关系, 模型能从中掌握关系之间的对应情况, 而轻而易举的推出结果, 模型通过互逆关系偷懒, 而并非掌握推断能力. 已经有人对FB15k进行了修正, 推出FB15k -237, 作者也相应的对WN18进行了调整, 推出了WN18RR.

Parameters

作者对比了DistMult和ConvE在FB15k - 237上不同Embedding Size的参数量:

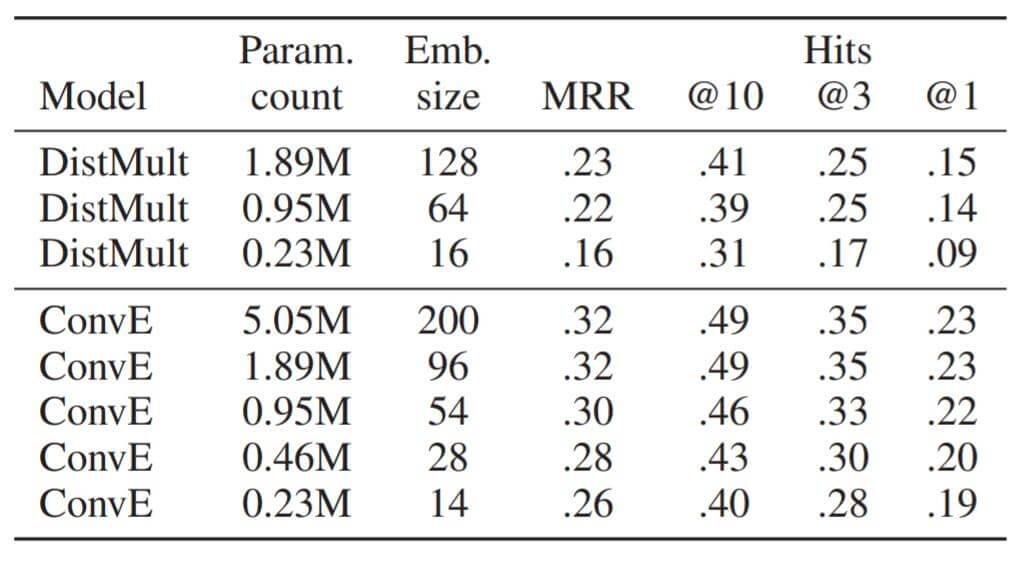
在相同参数量的情况下, ConvE能够腾出更多参数在Embedding Size上, 并且拥有比DistMult好的性能.

对于其他的超参设置, 作者在论文中指出, 大的卷积核效果不如多个小卷积核效果好(这点与CV中结论一致, 基本已经成常识了).

Inverse Model

虽然大家都已经知道在FB15k和WN18的测试集中存在大量的互逆关系, 但是从来没有人定量的对这个问题的严重性进行调查. 作者随意构造了一个基于规则的简单模型, 发现这个模型能随随便便在存在问题的数据集上取得非常棒的性能.

这个Inverse Model能在训练时自动从给定的两个关系对$r_1, r_2$ 中提取出来, 并检查它们是否是互逆关系. 在测试时, 模型能够自动的看三元组是否含有逆关系, 如果有的话则对最为匹配的$k$ 个逆关系进行排名, 然后从前$k$ 个排名中进行选择, 如果没有逆关系则随机从所有排名中选.

在后面的链接预测任务中, Inverse Model能够非常好的检查数据集是否存在大量的逆关系, 并评估这种情况的危害.

Link Prediction

在链接预测任务中, 作者分别在WN18, FB15k, WN18RR, FB15k - 237, YAGO3 - 10, Countries上做了实验.

WN18, FB15k:

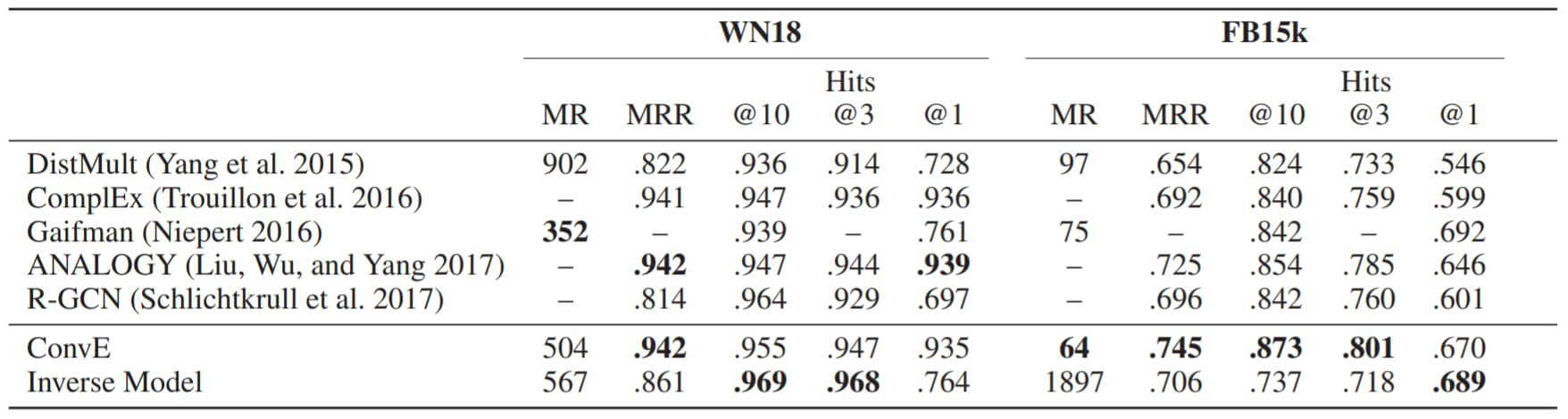
Inverse Model轻而易举的超过了许多模型.

下面是去除了互逆关系的WN18RR和FB15k - 237:

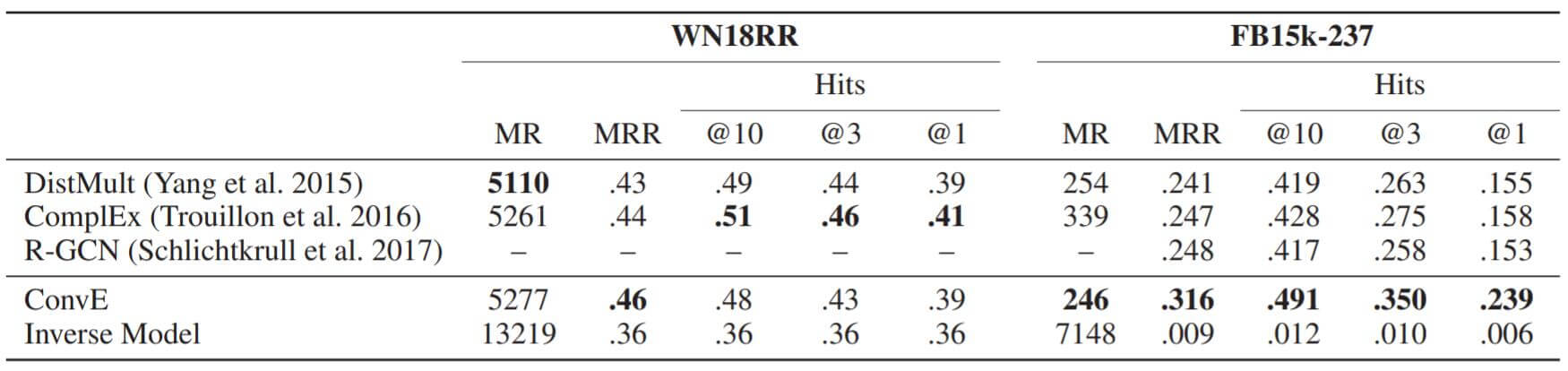
Inverse Model的性能一落千丈, 同时ConvE在这两个数据集上表现都非常不错, FB15k - 237上表现超过所有Baseline, WN18RR和其他模型也没有差太多.

YAGO3 - 10, Countries:

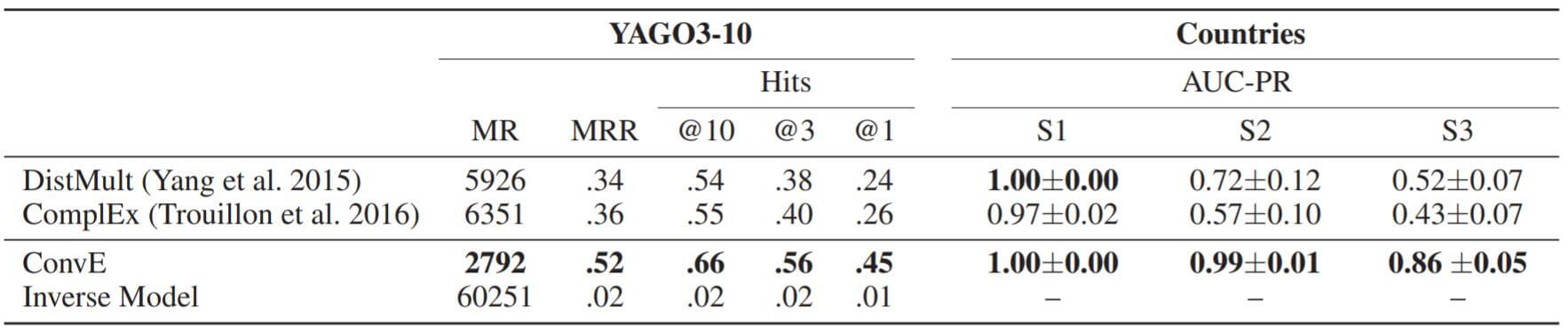
Ablation Study

作者对ConvE的组成因素挨个做了消融实验:

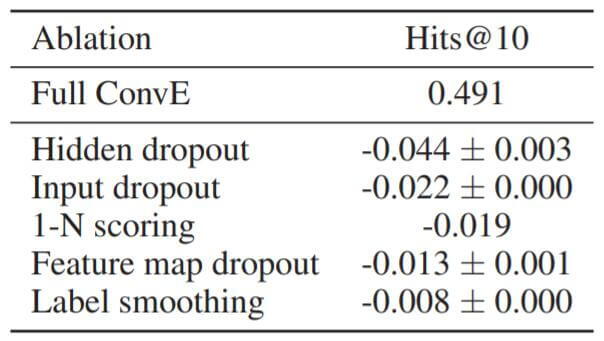
各种Dropout似乎对ConvE的影响很大, 1 - N Scoring的增益也不小, 标签平滑倒是不怎么重要.

Indegree and PageRank

Indegree

作者指出, YAGO3 - 10, FB15k - 237与WN18RR相比都具有非常高的关系入度, 并且ConvE在它们上面表现非常好. 作者假设, 像ConvE这样更加深层次的模型能更好的对高入度的关系建模.

基于这个假设, 作者将低入度的WN18(low - WN18)和高入度的(high - FB15k)进行转换, 变为高入度的WN18(high - WN18)和低入度的(low - FB15k), 然后观察ConvE在上面的表现. 作者发现在low - FB15k上, ConvE的表现逊于DistMult, 在high - WN18上表现强于DistMult. 这支持了作者的假设.

PageRank

PageRank是节点中心性的度量, PageRank越高, 节点的影响力就越大. 作者假设更深的模型在捕获约束上更有优势, 但更加难以优化.

作者仍然将ConvE和DistMult进行比对, 比较将DistMult换成ConvE后在不同数据集上Hits@10之间的差距:

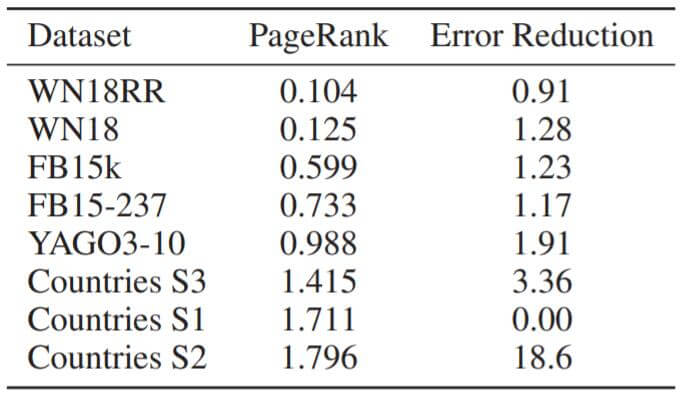
基本规律是PageRank越高, 错误减少的就越多, ConvE就越强大. 这也佐证了作者的猜想.

Summary

我认为作者在本文中的贡献如下:

1. ConvE将卷积的方法引入了KGE中.
2. 提供了去除互逆关系的WN18RR数据集.
3. 提出了1 - N Score的思想, 大大加速Evaluation的过程. 而且它还能移植到其他1 - 1 Score模型上.
4. 指出了卷积的高参数利用率, 为后续多种基于卷积的KGE方法打开了新的大门.

本文不仅仅是简单的将卷积引入, 在实验的证明思路也比较值得学习.