本文前置知识:
- ConvE
- Conv1d
2021.03.15: 指出权重共享并没有出现在源码中.
A Novel Embedding Model for Knowledge Base Completion Based on Convolutional Neural Network
本文是论文A Novel Embedding Model for Knowledge Base Completion Based on Convolutional Neural Network的阅读笔记和个人理解. 本文篇幅比较短, 模型比较简单.
Basic Idea
作者认为ConvE只考虑了局部不同维度的关系, 而没有考虑全局相同维度的关系, 这就需要一种方式在实体和关系之间捕获全局关系和过渡特性.
我个人的理解就是, 一般KGE都是用Link Prediction去训练模型, 只使用了头实体和关系的信息, 去预测尾实体. 但ConvKB能够同时使用头实体, 尾实体, 关系的信息.
ConvKB
ConvKB的方法是非常简单的.
假设头实体$h$, 关系$r$, 尾实体$t$, 先将$(h, r, t)$ 通过$k$ 维的Embedding, 得到$\left(\boldsymbol{v}_{h}, \boldsymbol{v}_{r}, \boldsymbol{v}_{t}\right)$, 并将其转为矩阵$\boldsymbol{A}=\left[\boldsymbol{v}_{h}, \boldsymbol{v}_{r}, \boldsymbol{v}_{t}\right] \in \mathbb{R}^{k\times 3}$. 作者使用多个$1\times 3$ 的Conv1d来捕捉三者同个维度上的全局信息, 其卷积核为$\omega$, 通过卷积运算能产生特征图$\boldsymbol{v}=\left[v_{1}, v_{2}, \ldots, v_{k}\right] \in \mathbb{R}^{k}$:
$$
v_{i}=g\left(\boldsymbol{\omega} \cdot \boldsymbol{A}_{i,:}+b\right)
$$
其中$b$ 为偏置项, $g$ 为激活函数, 这里用的是ReLU.
设$\Omega$ 为所有卷积核的集合, $\tau$ 为卷积核的数量, 则有$\tau =|\Omega|$. 那么将所有的卷积核扫描完后, 能产生$\tau$ 个大小为$k \times 1$ 的向量, 将他们Concat起来, 大小为$\mathbb{R}^{\tau k \times 1}$. 然后用一个权重向量$\mathbf{w}$ 来和Concat后的向量做点积, 得到分数.
看图总结一下, 图中取的$\tau=3$, $k=4$:
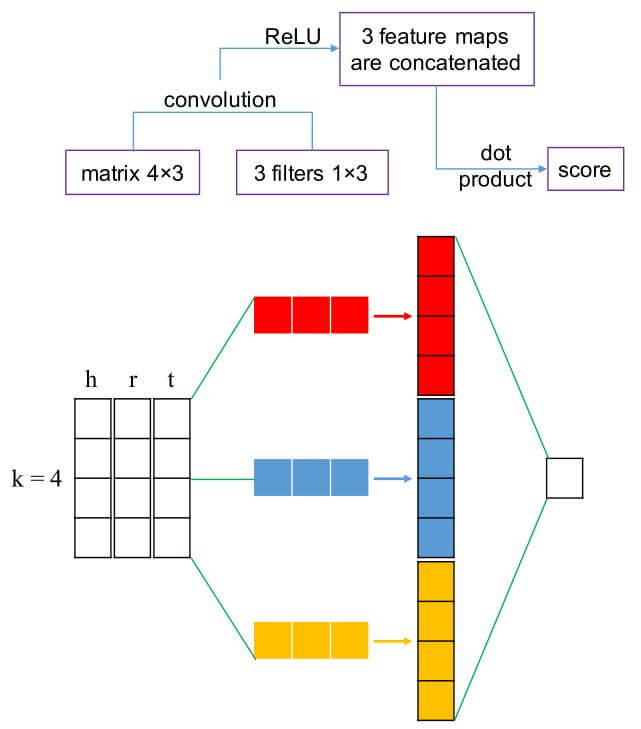
Score Function
打分函数为:
$$
f(h, r, t)=\operatorname{concat}\left(g\left(\left[\boldsymbol{v}_{h}, \boldsymbol{v}_{r}, \boldsymbol{v}_{t}\right] \ast \boldsymbol{\Omega}\right)\right) \cdot \mathbf{w}
$$
其中$\ast$ 代表卷积操作, $\Omega$ 和$\mathbf{w}$ 是参数共享, $\mathbf{w} \in \mathbb{R}^{\tau k \times 1}$. 打分函数的输出越小证明三元组越可靠.
虽然作者说可以”权重共享”, 但思考一下维度变换其实根本没法这么做(除非$k=3$).
并且作者开源代码也没有关于权重共享的任何内容.
作者还提到, 如果只使用一个卷积核$\omega=[1, 1, -1]$, 固定$b=0$, 令激活函数$g(x)=|x|$ 或 $g(x)=x^2$, 并使$\mathbf{w} = 1$, ConvKB将退化为TransE, 即$|h+r-t|$.
Loss Function
损失函数为:
$$
\begin{array}{c}
\mathcal{L}=\sum_{(h, r, t) \in\left\{\mathcal{G} \cup \mathcal{G}^{\prime}\right\}} \log \left(1+\exp \left(l_{(h, r, t)} \cdot f(h, r, t)\right)\right)
+\frac{\lambda}{2}||\mathbf{w}||_{2}^{2}
\end{array}
$$
$l_{(h,r,t)}$ 是一个符号:
$$
\ l_{(h, r, t)}=\left\{\begin{array}{l}
1 \text { for }(h, r, t) \in \mathcal{G} \\
-1 \text { for }(h, r, t) \in \mathcal{G}^{\prime}
\end{array}\right.
$$
$\mathcal{G}$ 代表知识图谱, $\mathcal{G’}$ 代表从知识图谱中生成的无效三元组集合.
损失函数大致的意思是, 模型能否根据ConvKB来区分三元组是否正确. 所以其实它的本质是一个二分类交叉熵.
后面加了正则项防止过拟合.
Experiment
作者把ConvKB在WN18RR和FB15k-237上做了链接预测的实验, 结果如下:
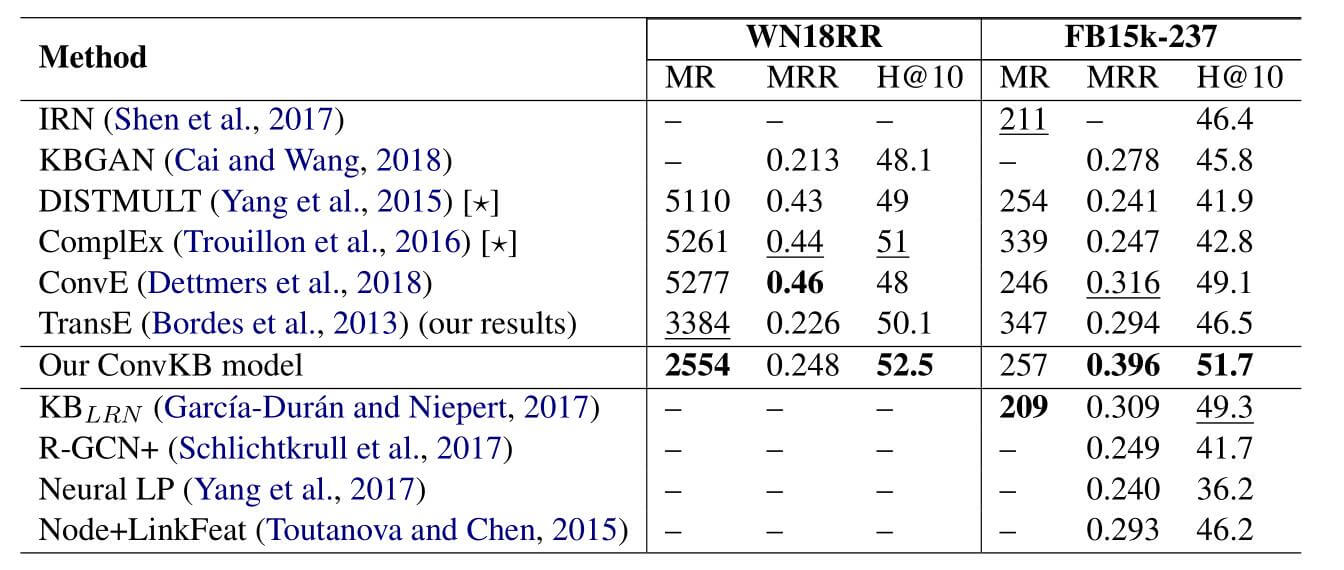
能看到, 相比于ConvE, ConvKB有相当大的提升, 作者还吐槽了ConvE在某些指标上甚至还没有TransE好.
一些超参数的设置细节不再列举了, 原文说的比较详细.
Summary
ConvKB没有使用Reshape, 不像ConvE那样提取Embedding间的局部信息, 而是通过Conv1d来提取包含尾实体的全局信息. 但实验列出的指标没有Hit@1和Hit@3, 不知道ConvKB在这两个指标上是否表现得也像Hit@10一样好.
另外, 我认为在$(h, r, t)$ 的每个相同Dimension上不一定有实质的联系, 可能是交错的, 所以可以考虑用Permutation之类的方式来尽可能消除这种可能性. 或者通过某些方式让CNN提取交错Dimension位置上的特征.

