RotatE: Knowledge Grpah Embedding by Relational Rotation Complex Space
本文是论文ROTATE: KNOWLEDGE GRAPH EMBEDDING BY RELATIONAL ROTATION IN COMPLEX SPACE的阅读笔记和个人理解.
Basic Idea
作者的出发点如下:
- 在许多任务中的成功推断都严重依赖于关系模式.
- 现有的Knowledge Embedding Model都不能对所有关系同时建模.
基于这两个出发点, 作者希望能构建出一种对所有关系建模的模型.
RotatE
Modeling and Inferring Relation Patterns
假设有三实体$x, y, z$, 存在关系$r$, 作者定义了如下三种关系的形式:
对称关系和反对称关系:
对称关系: 如果$x$ 能通过变换$r$ 得出$y$, 那么$y$ 必然能通过同样的$r$ 得出$x$.
反对称关系: 若$x$ 能通过$r$ 找到$y$, 那么$y$ 必然不能通过同样的$r$ 找到$x$, 或者说$y$ 对$x$ 必然不存在关系$r$.
即:
$$
\begin{aligned}
r(x, y) &\Rightarrow r(y, x) \\
r(x, y) &\Rightarrow \neg r(y, x)
\end{aligned}
$$
互逆关系:
如果$r_1$ 和$r_2$ 互为逆关系, $x$ 必然能通过$r_1$ 得到$y$, 同时$y$ 也能通过$r_1$ 的逆变换$r_2$ 得到$x$, 即:
$$
r_{2}(x, y) \Rightarrow r_{1}(y, x)
$$
组合关系:
如果$r_3$ 是由变换$r_1$ 和变换$r_2$ 组成的, 那么它们之间存在递进关系, 即:
$$
r_{2}(\mathrm{x}, \mathrm{y}) \wedge \mathrm{r}_{3}(\mathrm{y}, \mathrm{z}) \Rightarrow \mathrm{r}_{1}(\mathrm{x}, \mathrm{z})
$$
我这里将所有的”关系”都解释为”变换“, 是因为KGE模型的本质是在构造一种”变换方式“, 使得头实体尽可能的能够通过特定的关系变换后找到唯一对应尾实体.
而现有的方法往往不能对上述常见的三种关系模式进行建模:
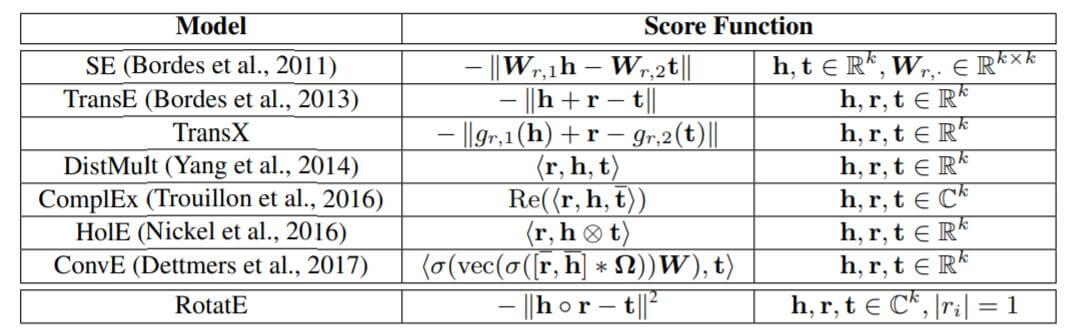
除了ConvE是神经网络型的KGE模型无法分析, 其他模型都没有同时对所有关系建模:
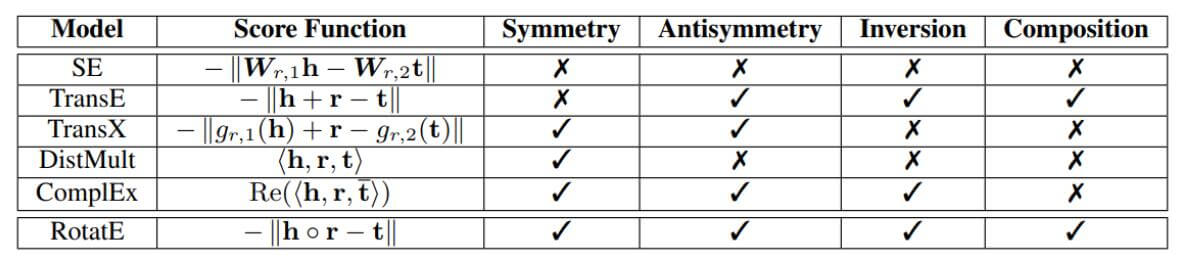
而作者接下来提出的RotatE却能处理列出的所有情况.
Modeling Relations as Rotations in Complex Vector Space
Euler’s Inspired
RotatE的灵感来源于欧拉公式:
$$
e^{i \theta}=\cos \theta+i \sin \theta
$$
在复数空间内, 虚数乘法的运算意义为旋转(Rotation), 这一特性能使RotatE很好地对作者所定义的关系进行建模, 记复数空间内的三点为$x, y, z$, 旋转角度为$\theta$:
- 对称关系: 将$x$ 旋转$\theta=\pi$ 得到$y$, 在$y$ 处再次旋转$\theta=\pi$ 回到$x$.
- 互逆关系: 将$x$ 旋转$\theta_1$ 得到$y$, 在$y$ 处旋转$\theta_2=-\theta_1$, 即反方向旋转$\theta_1$, 可以回到$x$.
- 组合关系: 将$x$ 先旋转$\theta_1$, 记为$y$, 再旋转$\theta_2$ 记为$z$. 该过程等价于从$x$ 处旋转$\theta_3=\theta_1+\theta_2$, 直接得到$z$.
因此, 我们只需要在复平面上做头实体$h$ 和关系$r$ 的元素按位乘就可以了:
$$
\mathbf{t}=\mathbf{h} \circ \mathbf{r}
$$
其中$\circ$ 代表Hadmard Product(元素按位乘). 因为关系变换被定义为旋转, 所以需要限制$\mathbf{r}$ 中的每个维度的$|r_i|=1$, 这样就可以让角度$\theta \in [-\pi, \pi]$.
距离函数被作者定义为:
$$
d_{r}(\mathbf{h}, \mathbf{t})=\lVert\mathbf{h} \circ \mathbf{r}-\mathbf{t}\rVert
$$
即头实体通过旋转后与三元组真实尾实体的距离越近越好.
Connection to TransE
TransE仅在一维数轴上做关系变换, 而将关系变换定义为旋转的RotatE可以在二维复平面上做关系变换:
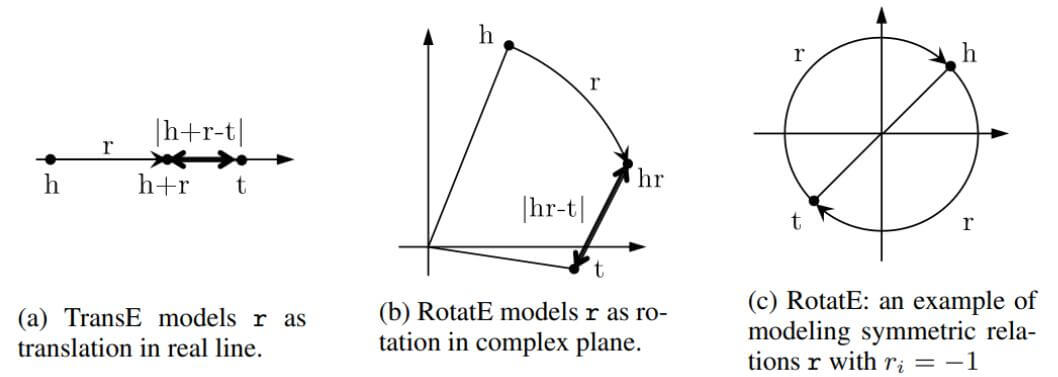
一维数轴的限制导致TransE无法处理对称关系, 除非将关系变为0向量, 但这会引入更多的问题.
Optimization
Loss Function
RotatE仍然采用类似TransE的Hinge Loss, 并加上负采样:
$$
L=-\log \sigma\left(\gamma-d_{r}(\mathbf{h}, \mathbf{t})\right)-\sum_{i=1}^{n} \frac{1}{k} \log \sigma\left(d_{r}\left(\mathbf{h}_{i}^{\prime}, \mathbf{t}_{i}^{\prime}\right)-\gamma\right)
$$
Self - Adversarial Negative Sampling
通常情况下, 模型认为打分函数越高的三元组越真实, 而模型已经知道打分比较低的三元组不真实了, 就没有必要过多的注意这类三元组. 而对于那些模型认为是正确, 实际是错误的三元组, 需要被模型提起注意.
所以作者按照如下分布采样:
$$
p\left(h_{j}^{\prime}, r, t_{j}^{\prime} \mid\left\{\left(h_{i}, r_{i}, t_{i}\right)\right\}\right)=\frac{\exp \alpha f_{r}\left(\mathbf{h}_{j}^{\prime}, \mathbf{t}_{j}^{\prime}\right)}{\sum_{i} \exp \alpha f_{r}\left(\mathbf{h}_{i}^{\prime}, \mathbf{t}_{i}^{\prime}\right)}
$$
其中$f_r$ 为KGE模型的打分函数, $\alpha$ 为采样率. 得分比较高的三元组更容易被采样到, 因为它们更容易把模型迷惑, 得分比较低的三元组将被少量采样到, 因为模型已经有一定能力判断它们是否正确.
因为每次负样本采样都是昂贵的, 不单是采样可以使用计算得出的概率, 它们还可以在计算Loss时复用, 将作为负样本的权重:
$$
L=-\log \sigma\left(\gamma-d_{r}(\mathbf{h}, \mathbf{t})\right)-\sum_{i=1}^{n} p\left(h_{i}^{\prime}, r, t_{i}^{\prime}\right) \log \sigma\left(d_{r}\left(\mathbf{h}_{i}^{\prime}, \mathbf{t}_{i}^{\prime}\right)-\gamma\right)
$$
打分本身较低的三元组所对应的负采样权重较低, 打分较高的三元组权重较高. 即越容易迷惑模型的三元组权重越高.
Experiments
详细的超参设置请参照原论文.
除了RotatE, 作者还提出了其变体pRotatE, 它的实体嵌入的模长是被限制的, 即$|h_i| = |t_i| = C$, 它的距离函数被相应的改写为$2C \lVert\sin \frac{\theta_h + \theta_r - \theta_r}{2}\rVert$.
理论上它与RotatE一样, 也能同时处理多种关系. 但因缺少了模长信息, 所以它处理的效果应该会稍差一些. 反过来看, pRotatE也能说明旋转建模所带来的强大能力.
Main Results
作者在FB15k, WN18上的实验结果如下:
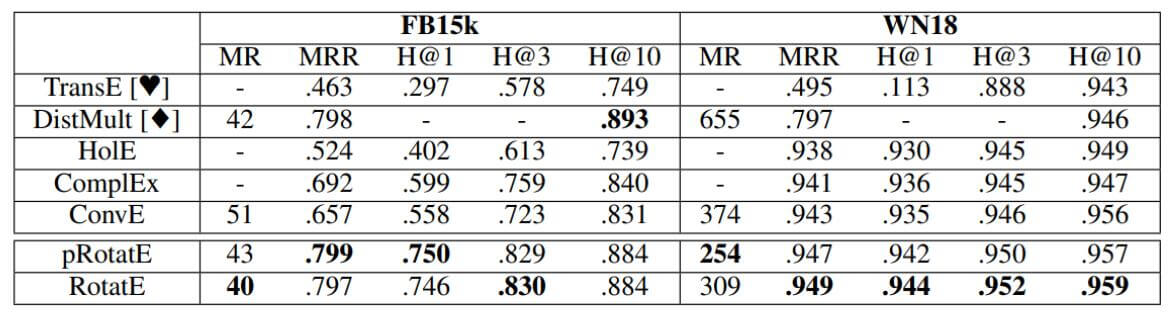
RotatE表现出很强大的性能, 和变体差不多.
作者在FB15k - 237, WN18RR上的实验结果如下:
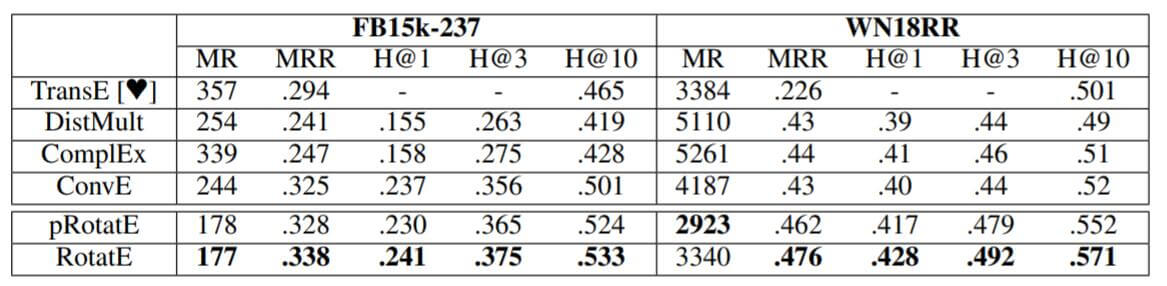
RotatE比ConvE的结果要好一些. 但对于MR来说, RotatE的结果要好得多, 说明ConvE对于某些关系学习到的特征是模糊的.
Relation Pattern Experiments
在Countries上的结果如下:
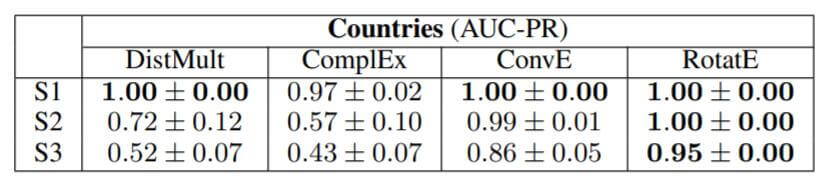
在最困难的S3上, RotatE要显著好于其他方法.
WN18上的各类关系所对应的$r$ 值如下:
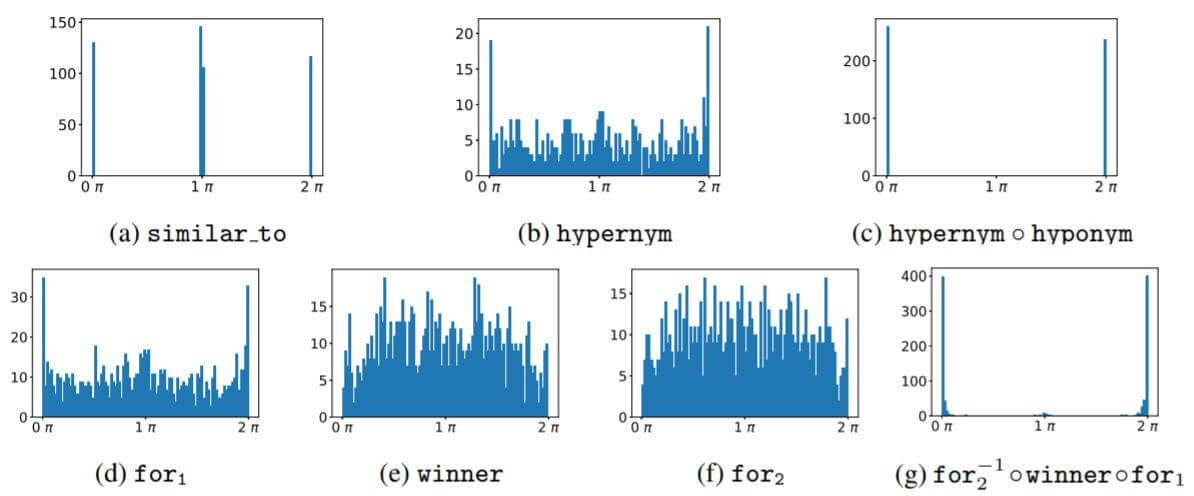
similar_to是明显的对称关系, hypernym, hyponym是一对明显的逆关系, 二者的组合刚好是什么也不做, for1, for2, winner三者的组合也被学习到了. RotatE很好的掌握了这些关系的变换方式.
Negative Sampling Techniques
分别在3个基准数据集上, 三种负采样的效果如下:

明显作者提出的自对抗负采样效果要好.
为了能更公平的对比TransE, ComplEx, RotatE, 作者将自对抗负采样同时用于其他两种方法, 结果如下:

RotatE仍然是最优秀的方法. 但TransE比RotatE在S3上稍好一些, 作者解释为Countries不包含TransE最不擅长的对称关系, 在这个数据集上显示出TransE的强大.
Results by Relation Category
作者在FB15k上按照多类别统计的实验结果如下:
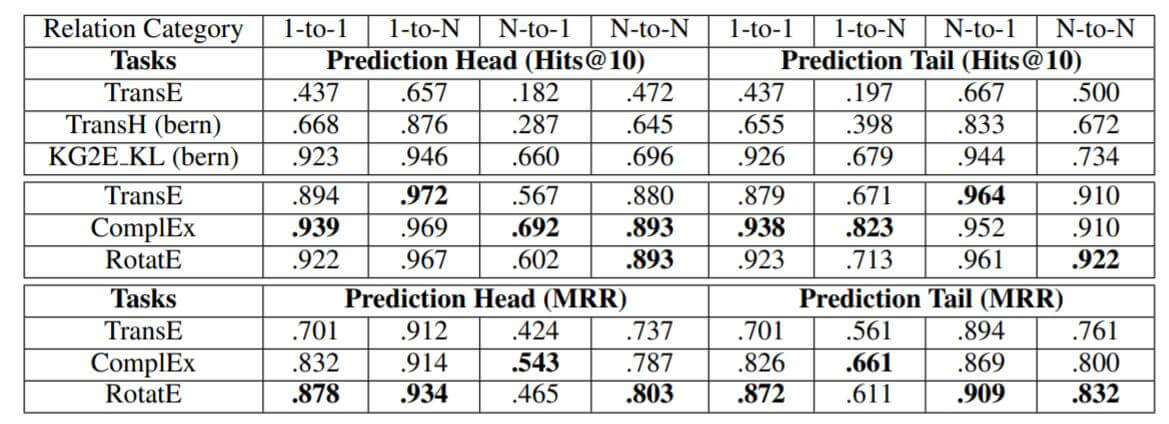
其实从原理上来讲, RotatE应该不擅长处理一对多, 多对一, 多对多关系. 不过看起来结果还不错.
个人观点: 可能是RotatE采用了比较大的Embedding Size, 在高维中或许点和点之间的距离比想象的要远, 即这些点在高维空间中可能是可分的.
Summary
在联结主义被大肆吹鼓的今天看到一篇这样的文章实属不易.
RotatE将关系变换定义为旋转, 在复数空间建模, 建模的方式简洁而优雅. 同时提出了一种优化的自对抗负采样算法, 能让模型聚焦于更容易混淆的三元组. RotatE还是一种线性复杂度的算法, 所以易于扩展到大规模的KG中.
其实在后面Appendix还有在YAGO3 - 10上做的实验, 还有自对抗负采样的Ablation Study, 算是很扎实了.
虽然RotatE十分简洁, 但它仍然具有以下缺点:
- 与TransE相同, 只能对一对一关系建模. 这个缺陷在实验中并没有被很好的体现, 我认为是较大的Embedding Size遮盖了这个缺陷.
- 旋转操作并不能区分关系变换的前后顺序. 例如”父亲的儿子”和”儿子的父亲”在旋转中是一样的, 因为$\theta_3 = \theta_1+\theta_2=\theta_2+\theta_1$.

