本文前置知识:
A Novel Global Feature-Oriented Relational Triple Extraction Model based on Table Filling
本文是论文A Novel Global Feature-Oriented Relational Triple Extraction Model based on Table Filling的阅读笔记和个人理解, 论文来自EMNLP 2021.
Basic Idea
基于填表的RTE方法展示出优越的性能, 然而, 现有的方法并没有发挥表格的全部潜力, 它们大多聚焦于表格中的局部信息, 而非Relation和Token Pair的全局关联.
例如, 在句子Edward Thomas and John are from New York City, USA.中, 抽取出(Edward Thomas, live_in, New York) 有益于抽取出(John, live_in, USA), 反之亦然. 因为它们的(Subject, Object) 是高度相同的, 它们的Subject均为Person, Object均为Location.
并且, 这两个三元组又有益于抽取出(New York, located_in, USA), 因为located_in 要求Subject和Object均为Location, 且它的语义与live_in 相关, live_in 要求Object为Location, 所以有益.
为此, 作者希望提出一种充分挖掘表格中全局信息的填表式RTE方法.
GRTE
Table Filling Strategy
对于句子$S = \set{w_1, w_2, \dots, w_n}$, 和每种关系$r$, 都维护一张大小为$n \times n$ 的二维表$table_r$, 填表法便是将每个表中的元素填上一个正确的标签.
作者预先定义好如下标签:
$$
L = \set{\text{“N/A”, “MMH”, “MMT”, “MSH”, “MST”, “SMH”, “SMT”, “SS”}}
$$
表的第$i$ 行第$j$列对应着Token Pair $(w_i, w_j)$ 之间的标签类别.
若$l \in \set{\text{“MMH”, “MMT”, “MSH”, “MST”, “SMH”, “SMT”}}$ 则意味着$(w_i, w_j)$ 是一对三元组对应的Subject和Object.
标签中的第一个字母代表Subject的实体类型是多Token还是单Token, $\text{M}$ 代表多Token实体, $\text{S}$ 代表单Token. 同理, 第二个标签代表Object的实体类型. 最后一个字母则代表$w_i, w_j$ 同是实体的头Token或尾Token, $\text{H}$ 代表头, $\text{T}$ 代表尾. 此外, $l=\text{“SS”}$ 代表$(w_i, w_j)$ 是一个实体对, 其两个实体都是单Token实体, $l=\text{“N/A”}$ 代表$(w_i, w_j)$ 间不存在关系.
只要有其中一个是单Token实体, 另外一个是多Token实体, 则单Token即被看做是头也被看做是尾.
还是本文开头的那个例子, 作者将标签套入其中, 详细说明:
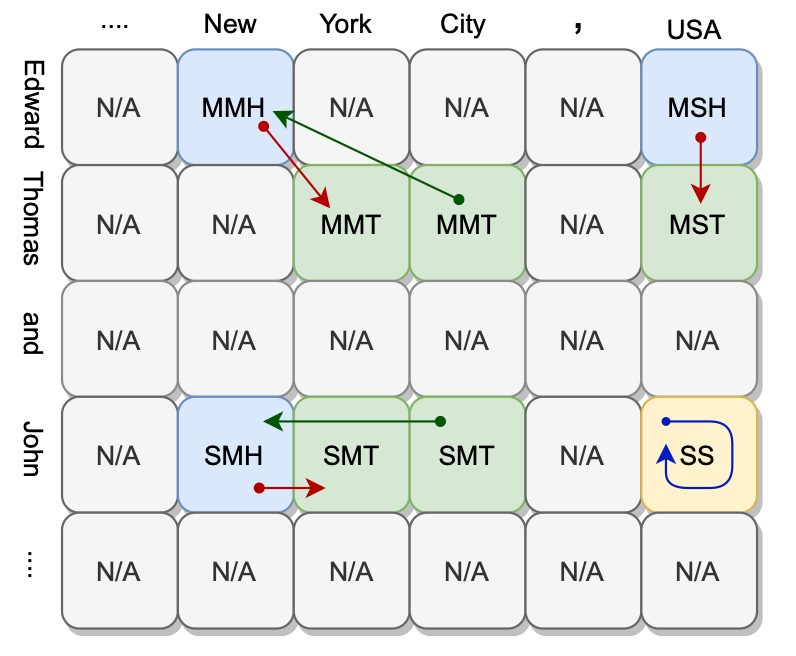
对于句子Edward Thomas and John are from New York City, USA., 它的实体对可以被这样确定下来:
| 行 | 列 | 标签 | 行 | 列 | 标签 | 三元组 | 三元组类型 |
|---|---|---|---|---|---|---|---|
Edward | New | MMH | Thomas | City | MMT | (Edward Thomas, New York City) | M - M |
Edward | New | MMH | Thomas | York | MMT | (Edward Thomas, New York) | M - M |
Edward | USA | MSH | Thomas | USA | MST | (Edward Thomas, USA) | M - S |
John | New | SMH | John | City | SMT | (John, New York City) | S - M |
John | New | SMH | John | York | SMT | (John, New York) | S - M |
John | USA | SS | - | - | - | (John, USA) | S - S |
在这种填表策略下, 只需要对每个关系填一张表, 即需要填$n^2|R|$ 个元素, 而不是TPLinker中的两张表, 即$(2|R| + 1) \frac{n^2 +n} {2}$ 个元素, 因此需要填的元素数量是比TPLinker要少的, $(2|R| + 1) \frac{n^2 +n} {2} > n^2|R|$.
此外, 这种特殊的标签设置, 建模了Token Pair之间的全局关联, 因为模型除了必须同时知道Subject和Object是哪种类型的实体.
Model Details
模型细节主要分为TFG, GFM, TG三个部分.
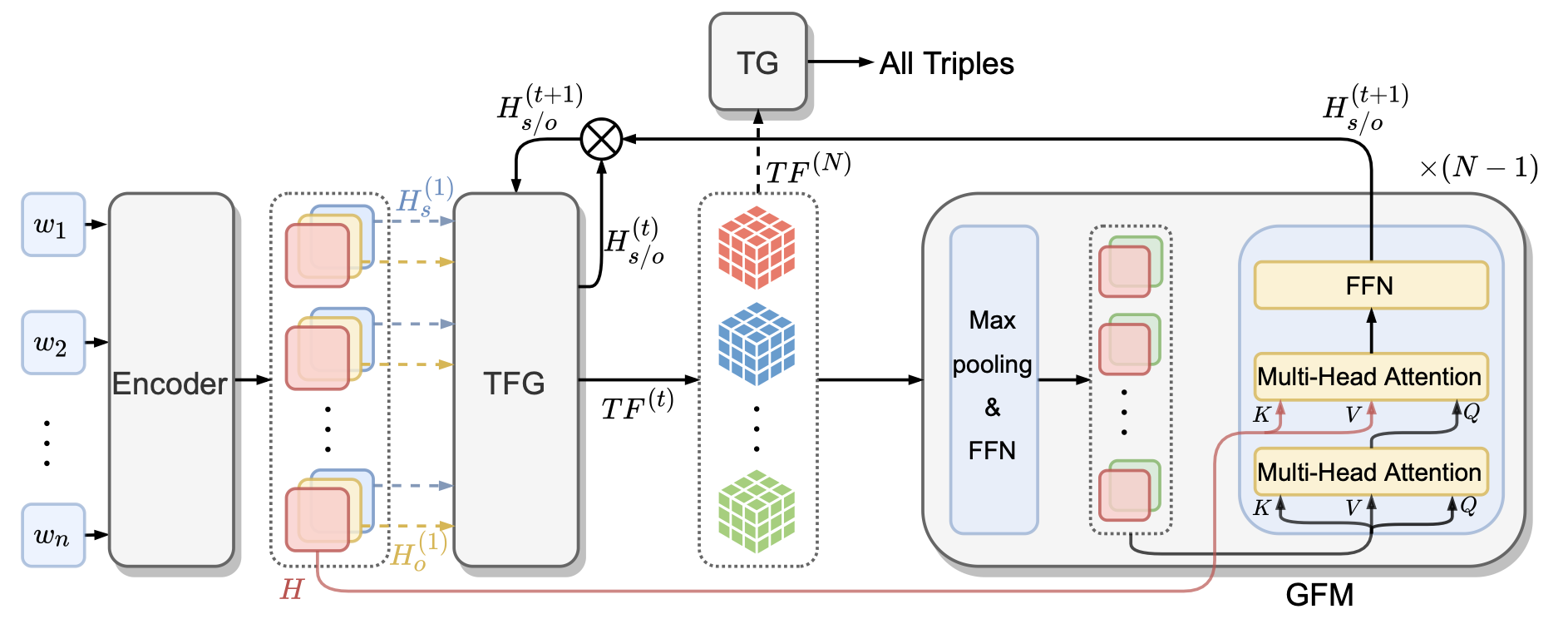
Encoder Module
用BERT作为预训练模型, 获得句子的表示$H \in \mathbb{R}^{n \times d_h}$, 然后用两个独立的FFN生成初始的Subject的特征$H_s^{(1)}$和Object的特征$H_o^{(1)}$:
$$
\begin{aligned}
&H_{s}^{(1)}=W_{1} H+b_{1} \\
&H_{o}^{(1)}=W_{2} H+b_{2}
\end{aligned}
$$
其中$W_1, W_2 \in \mathbb{R}^{d_h \times d_h}, b_1, b_2 \in \mathbb{R}^{d_h}$ 为可训练参数.
Table Feature Generation Module

TFG Module的输入$H_s, H_j$ 来自于TFG和GFM之间的迭代过程, 故记第$t$ 轮的Subject和Object的特征分别为$H_s^{(t)}, H_j^{(t)}$.
TFG会根据每种关系$r$, 利用Subject和Object特征分别生成一张Token Pair$(w_i, w_j)$ 之间的二维表格特征$TF_r^{(t)}$.
在表$TF_r^{(t)}$ 中, 它的每个元素$TF_r^{(t)}(i, j)$ 的计算方式如下:
$$
T F_{r}^{(t)}(i, j)=W_{r} \operatorname{ReLU}\left(H_{s, i}^{(t)} \circ H_{o, j}^{(t)}\right)+b_{r}
$$
其中, $\circ$ 代表逐元素点乘, $W_r, b_r$ 为可训练参数.
$TF^{(t)}_r \in \mathbb{R}^{n \times n \times |L|}, TF^{(t)} \in \mathbb{R}^{n \times n \times (|L| \times |R|)}$, 而且$TF_r^{(t)}$ 与$table_r$ 是同型的.
Global Feature Mining Module
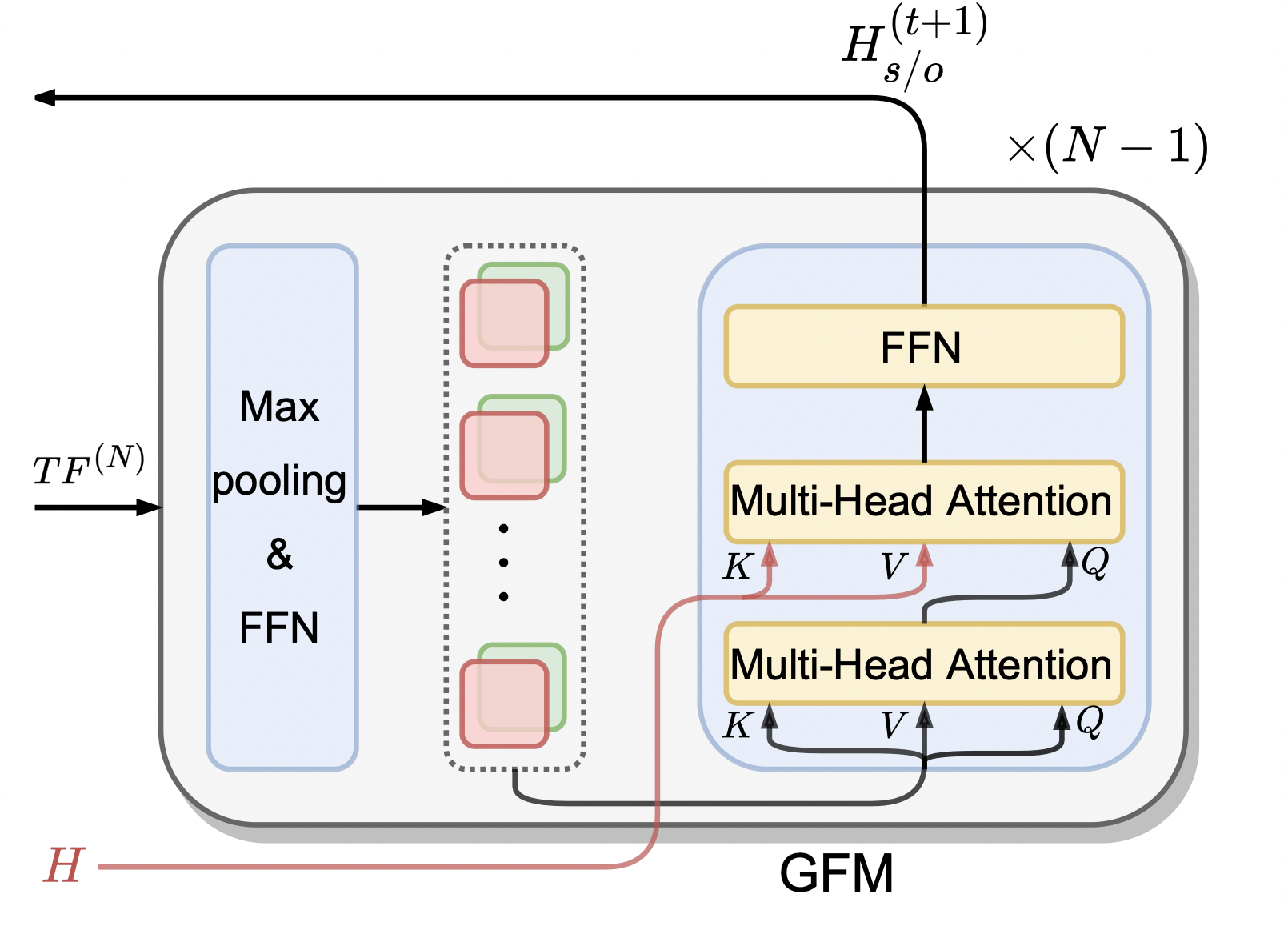
GFM Module目的是同时考虑所有关系, 挖掘表格全局特征, 分三步走.
Step 1, 整合表格特征.
我们把所有的关系$r$ 下的表格特征视为一个整体$TF^{(t)}$, 分别对所有关系下Subject / Object的特征做最大池化, 获得Subject / Object全局特征, 然后过一层线性层, 获得全局关系下的Subject / Object表特征$TF_{s/o}^{(t)}$:
$$
\begin{aligned}
&T F_{s}^{(t)}=W_{s} \underset{s}{\operatorname{maxpool}}\left(T F^{(t)}\right)+b_{s} \\
&T F_{o}^{(t)}=W_{o} \underset{o}{\operatorname{maxpool}}\left(T F^{(t)}\right)+b_{o}
\end{aligned}
$$
其中, $W_s, W_o \in \mathbb{R} ^{(|L| \times |R|) \times d_h}, b_s, b_o \in \mathbb{R}^{d_h}$ 为可训练参数.
$TF^{(t)} \in \mathbb{R}^{n \times n \times (|L|\times |R|)}, \underset{s/o}{\operatorname{maxpool}}(TF^{(t)}) \in \mathbb{R}^{n \times (|L| \times |R|)}$, 所以经过线性层$W_{s/o}$ 后维度为$ TF_{s/o}^{(t)} \in \mathbb{R}^{n \times d_h}$, 大小又回到了$H$ 的大小.
此外, 将所有关系的表特征放在一起, 建立了Relation之间的全局关联.
Step 2, 挖掘全局特征.
用多头自注意力重新分别获得Subject / Object视角下的表特征表示$\hat{T F}_{s/o}^{(t)}$, 然后用跨注意力以$\hat{T F}_{s / o}^{(t)}$ 为Query, 用Encoder输出的Token表示$H$ 为Key和Value, 获得Subject / Object视角下的更好的原Token表示$\hat{H}_{(s / o)}^{(t+1)}$, 最后经过一个线性层收尾:
$$
\begin{aligned}
\hat{T F}_{s / o}^{(t)} &=\text {MultiHeadSelfAtt}\left(T F_{s / o}^{(t)}\right) \\
\hat{H}_{(s / o)}^{(t+1)} &=\operatorname{MultiHeadAtt}\left(\hat{T F}_{s / o}^{(t)}, H, H\right) \\
H_{(s / o)}^{(t+1)} &=\operatorname{ReLU}\left(\hat{H}_{(s / o)}^{(t+1)} W+b\right)
\end{aligned}
$$
其中$W, b$ 为可训练参数.
两次注意力, 第一次是自注意力, 是对全局特征$T F_{s / o}^{(t)}$ 的内部重整, 挖掘Relation的全局关联. 第二次是跨注意力, 是利用全局特征对原始Token表示的重整, 挖掘Token Pair之间的全局关联.
Step 3, 整合Subject / Object特征.
参考Transformer, 用LayerNorm和残差连接缓解梯度消失:
$$
H_{(s / o)}^{(t+1)}=\operatorname{LayerNorm}\left(H_{(s / o)}^{(t)}+H_{(s / o)}^{(t+1)}\right)
$$
如果把第二步和第三步视为一个Block, 则Transformer Decoder Layer完全相同, 只需要反复用一个Decoder Layer迭代即可.
GFM Module的最终输出$H_{(s / o)}^{(t+1)} $ 将会被重新送入TFG Module生成新的表特征$TF^{(t+1)}$, 进入下一轮迭代.
Triple Generation Module
TG Module的任务就是结合我们前面提到的Table Filling Strategy, 来解码出句子中所有的三元组.
由最后一次迭代时TFG Module生成的表格特征$TF^{(N)}$ 作为输入, 为每个关系$r$ 下的表的每个格子$T F_{r}^{(N)}(i, j)$ 打上标签,
$$
\begin{aligned}
\hat{\operatorname{table}}_{r}(i, j) &=\operatorname{softmax}\left(T F_{r}^{(N)}(i, j)\right) \\
\operatorname{table}_{r}(i, j) &=\underset{l \in L}{\operatorname{argmax}}\left(\hat{\operatorname{table}}_{r}(i, j)[l]\right)
\end{aligned}
$$
其中, $\hat{\operatorname{table}}_{r}(i, j) \in \mathbb{R}^{|L|}$, $\operatorname{table}_{r}(i, j)$ 是Token Pair $(w_i, w_j)$ 在关系$r$ 下的标签.
对于作者设计的标签, 伪代码如下:

其实伪代码并不复杂. 对于每张关系表, 都使用启发式最近匹配算法, 有三种搜索方式:
- Forward Search: 找到离标签尾为H的格子最近的标签尾为T且前缀与前者相同的格子, 解码作为一个三元组, 然后找下一个标签尾为H的格子.
- Reverse Search: 与前者相反, 找到离标签尾为T的格子最近的标签尾为H且前缀与前者相同的格子, 解码作为一个三元组, 然后找下一个标签尾为T的格子. 与前者刚好互为补充.
- Single Token Pair: 找到标为SS的格子, 两个实体Token均为单个Token, 按行列直接解码出一个三元组, 然后找下一个SS格子.
其实Reverse Search的情况只是用来处理嵌套实体的, 如果数据中没有过多的嵌套实体, 可以去掉Reverse Search.
其实这三种方式分别就应着用来说明Table Filling Strategy例子图中的三种箭头, 分别对应着不同的解码方式:

红箭头为Forward Search, 绿箭头为Reverse Search, 蓝箭头为Single Token Pair.
Loss Function
表格的标签学习是一个多分类任务, 损失函数就用多分类交叉熵:
$$
\begin{aligned}
\mathcal{L} &=\sum_{i=1}^{n} \sum_{j=1}^{n} \sum_{r=1}^{|R|}-\log p\left(y_{r,(i, j)}=t a b l e_{r}(i, j)\right) \\
&=\sum_{i=1}^{n} \sum_{j=1}^{n} \sum_{r=1}^{|R|}-\log t a \hat{b} l e_{r}(i, j)\left[y_{r,(i, j)}\right]
\end{aligned}
$$
其中$y_{r, (i, j)} \in [1, |L|]$ 是$(w_i, w_j)$ 在关系$r$ 下的标签索引.
Experiments
详细的参数设置请参照原论文.
Datasets
数据集采用NYT24, WebNLG以及它们的部分匹配版本, 除此外还有NYT29, 它们的统计信息如下:

NYT29的规模比NYT24要大一些.
Experimental Results
主试验和消融实验放在一起了.
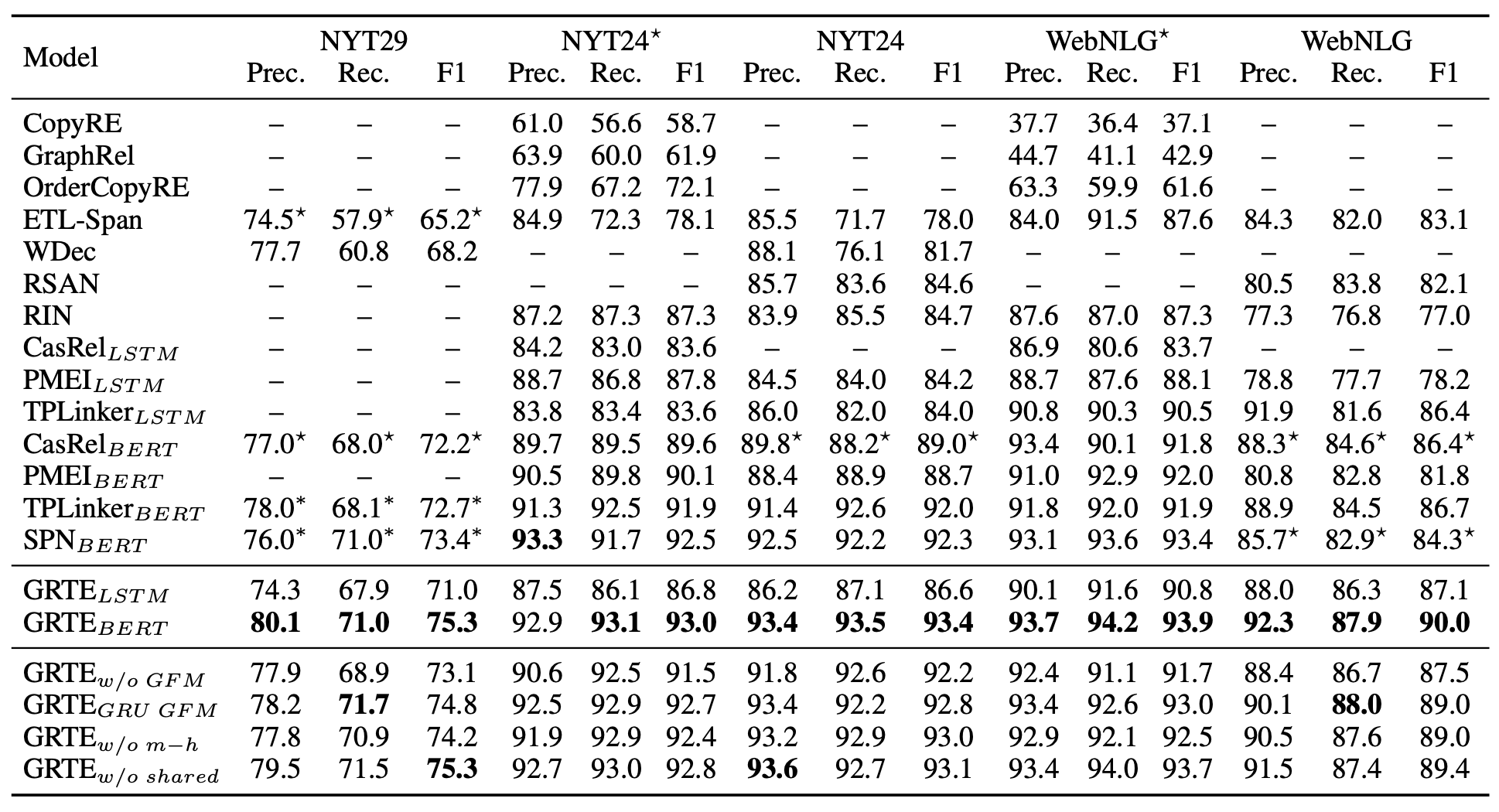
主试验结果上来看自然是达到了SOTA. 精度和召回都比较高. 在使用LSTM作为特征抽取器的情况下能够超过CasRel和TPLinker.
消融实验各个模型代表的是:
- GRTE w/o GFM: 去掉GFM模块, 即去掉挖掘表格特征的迭代过程.
- GRTE GRU GIF: 用GRU代替GFM中的Transformer Decoder完成迭代过程.
- GRTE w/o m-h: 不用多头注意力而单头注意力.
- GRTE w/o shared: 在TFG和GFM中不共享参数, 即每轮迭代都使用不同的参数.
第2, 3个实验体现了Transformer本身和多头注意力的效果, 而第1个实验体现了迭代过程的作用, 迭代过程还是起到了相当大的作用, 第4个实验体现了共享迭代过程参数的作用, 说明继续往上加参数容易过拟合, 共享参数就很好了.
GRTE在不同数据集和不同迭代次数的F1曲线如下:
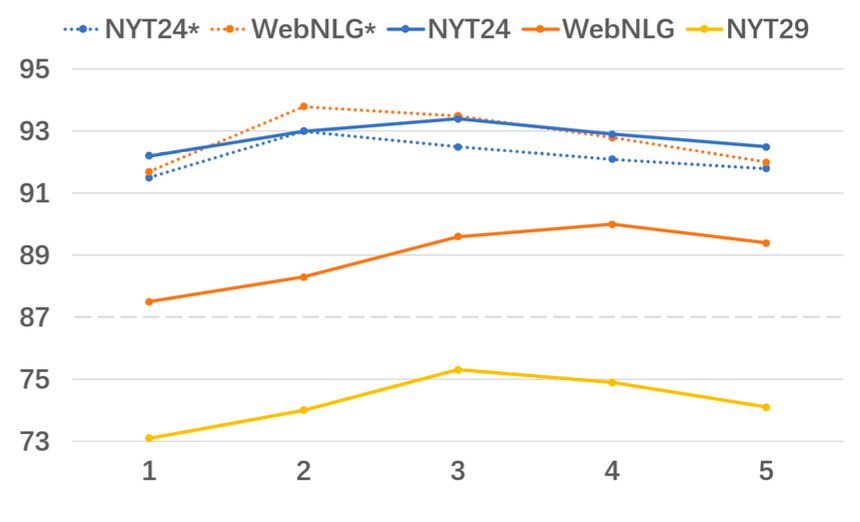
明显的能够看到, 对于不同数据集, 随着迭代次数上升到2, 3, 4时效果比迭代1次要好, 可以说明GRTE中迭代的必要性和有效性.
Analyses on Different Sentence Types
按三元组类型和句子中包含的三元组个数分类, 结果如下:

各类别下表现都比较好.
Analyses on Computational Efficiency
关于迭代, 很容易被人质疑效率问题. 所以作者对比了NYT和WebNLG上的模型参数量和推理时间:
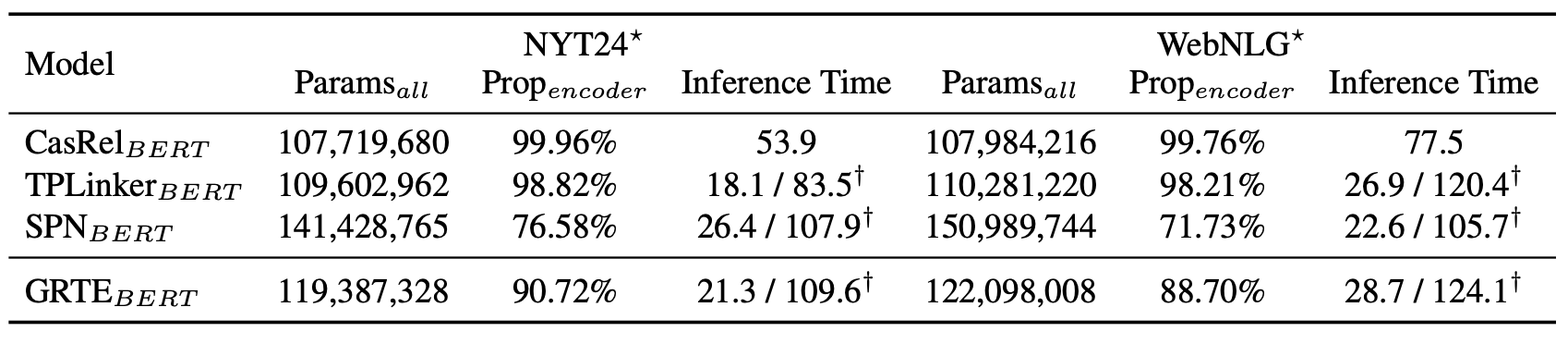
看上去推理时间是和SPN, TPLinker相当的, 并且归功于共享迭代模块的参数, 使得总参数量不如SPN高.
Summary
GRTE从三元组之间的相关性出发, 填补了前人忽视填表式方法中全局信息的空缺. 该方法基于全局特征, 通过独特的反复迭代方式不断提炼, 并从Relation的全局关联和Token Pair的全局关联两个方面挖掘表格中的全局特征, 也就是Generate - Mine - Integrate 过程.
标签的设定非常新颖, 建立了不同Token Pair之间的联系, 要求模型必须知道一对实体的信息才可以打标签, 并且对于每个关系只需要用一张表就能搞定了, 共享迭代模块的参数减少了参数效率方面的疑虑.

