本文前置知识:
Composition-based Multi-Relational Graph Convolutional Networks
本文是论文Composition-based Multi-Relational Graph Convolutional Networks的阅读笔记和个人理解.
Basic Idea
作者观察到, 现在GCN在图建模中存在两个问题:
现实世界中的图经常是有向图, 但现在图领域的研究常常专注于简单的无向图问题.
GCN的过参数化问题很严重, 并且只学习节点表示限制了模型表达.
作者希望提出一种对节点和关系联合嵌入的GCN模型来应对上述问题.
CompGCN
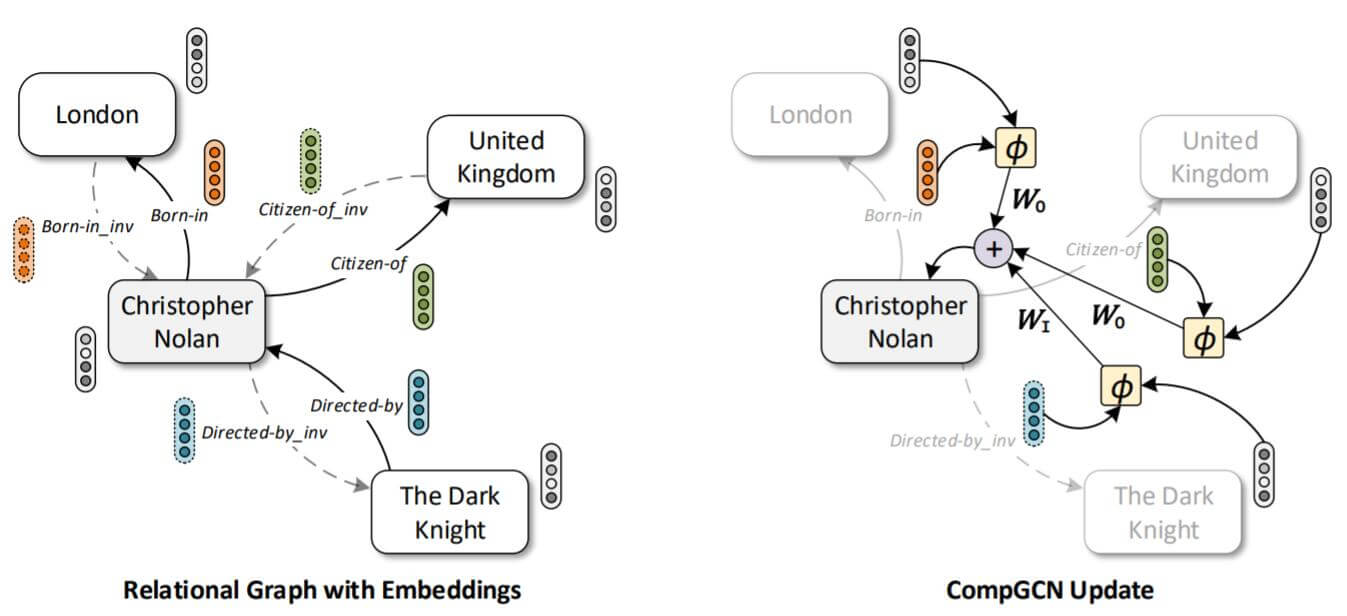
GCN and R - GCN
对于图$\mathcal{G}=(\mathcal{V}, \mathcal{E}, \mathcal{X})$, $\mathcal{V}, \mathcal{E}, \mathcal{X}$ 分别代表图中存在的顶点, 边, 和节点的初始特征.
让我们先来回顾一下经典的GCN的节点特征更新方程:
$$
\boldsymbol{H}^{k+1}=f\left(\hat{\boldsymbol{A}} \boldsymbol{H}^{k} \boldsymbol{W}^{k}\right)
$$
其中$\hat{\boldsymbol{A}}$ 是由度矩阵和自邻接矩阵归一化得到的.
在R - GCN中, 引入了对不同关系$\mathcal{R}$ 的特化处理, 图结构变为了$\mathcal{G}=(\mathcal{V}, \mathcal{R}, \mathcal{E}, \mathcal{X})$:
$$
\boldsymbol{H}^{k+1}=f\left(\hat{\boldsymbol{A}} \boldsymbol{H}^{k} \boldsymbol{W}_{r}^{k}\right)
$$
其中, $\boldsymbol{W}_r$ 为关系特化的变换矩阵.
但和大多数只嵌入节点的常规GCN方法不同, CompGCN同时嵌入节点和关系, 图结构信息变为$\mathcal{G}=(\mathcal{V}, \mathcal{R}, \mathcal{E}, \mathcal{X}, \mathcal{Z})$, $\mathcal{Z}$ 代表初始化的关系特征.
边的种类也被作者额外区分, 能对逆边和自环边加以区分, 即:
$$
\left.\mathcal{E}^{\prime}=\mathcal{E} \cup\left\{\left(v, u, r^{-1}\right) \mid(u, v, r) \in \mathcal{E}\right\} \cup\{(u, u, \top) \mid u \in \mathcal{V})\right\}
$$
相应的, 关系也被加以区分, 即$\mathcal{R}^{\prime}=\mathcal{R} \cup \mathcal{R}_{i n v} \cup\{\top\}$, 其中$\mathcal{R}_{i n v}=\left\{r^{-1} \mid r \in \mathcal{R}\right\}$.
Relation - Based Composition
引入关系嵌入后, 与KGE方法一样, 作者利用关系嵌入$\mathbf{e}_s$ 和实体嵌入$\mathbf{e}_r$ 的组合操作将节点和关系的信息作为整体共同$\mathbf{e}_o$, 纳入GCN的更新方程:
$$
\boldsymbol{e}_{o}=\phi\left(\boldsymbol{e}_{s}, \boldsymbol{e}_{r}\right)
$$
其中, $\phi: \mathbb{R}^{d} \times \mathbb{R}^{d} \rightarrow \mathbb{R}^{d} $ 是关系和实体嵌入的组合方式.
将关系表示为Embedding减轻了图神经网络中针对关系的过参数化问题.
我个人的理解是, 在R - GCN中, 关系特化以变换矩阵$\boldsymbol{W}_r$ 的形式存在, 而CompGCN中以Embedding的形式存在, 减少了每种关系所对应的参数个数. Embedding是信息的低维表征, 万物皆可Embedding.
作者尝试了三种实体关系组合方式:
- Subtraction(Sub): $\phi\left(\mathbf{e}_{s}, \mathbf{e}_{r}\right)=\mathbf{e}_{s}-\mathbf{e}_{r}$.
- Multiplication(Mult): $\phi\left(\boldsymbol{e}_{s}, \boldsymbol{e}_{r}\right)=\boldsymbol{e}_{s} \ast \boldsymbol{e}_{r}$.
- Circular - correlation(Corr): $\phi\left(\boldsymbol{e}_{s}, \boldsymbol{e}_{r}\right)=\boldsymbol{e}_{s} \star \boldsymbol{e}_{r}$.
分别是相减, 相乘, 循环相关运算. 循环相关运算出自论文Holographic embeddings of knowledge graphs, 即HoLE的论文. 三阶时的计算方法与行列式的主对角线计算中组合方式是相似的:
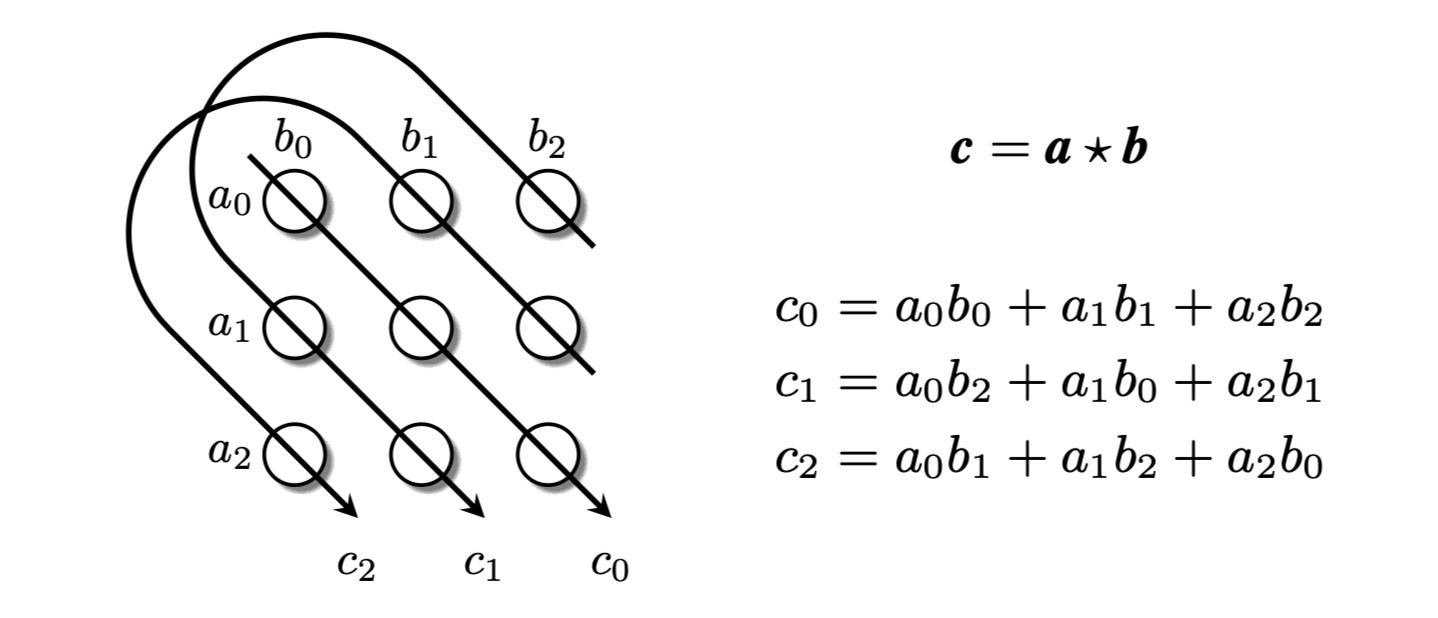
循环相关运算相比于前两种更为复杂, 考虑了更多向量间的不同组合方式.
通过关系实体组合操作, 关系和实体的嵌入组合特征将在同一特征空间下对节点信息更新.
CompGCN Update Equation
普通GCN的节点表示更新方程如下:
$$
\boldsymbol{h}_{v}=f\left(\sum_{(u, r) \in \mathcal{N}(v)} \boldsymbol{W}_{r} \boldsymbol{h}_{u}\right)
$$
其中, $\mathcal{N}(v)$ 是节点$v$ 的出边邻居, $(u,r)$ 是邻居节点和相对应的和关系. $\boldsymbol{h}_u$ 为节点$u$ 的特征.
而CompGCN引入关系实体嵌入的组合后, 的节点更新方式如下:
$$
\boldsymbol{h}_{v}=f\left(\sum_{(u, r) \in \mathcal{N}(v)} \boldsymbol{W}_{\lambda(r)} \phi\left(\boldsymbol{x}_{u}, \boldsymbol{z}_{r}\right)\right)
$$
其中$\lambda(r)$ 针对边的种类做了特化, 同一种关系在不同的边类型上也许会得到区分. 作者将边分为出边, 入边, 和自环边三种. 在这里$\lambda(r)=\text{dir}(r)$:
$$
\boldsymbol{W}_{\mathrm{dir}(r)}=\left\{\begin{array}{ll}
\boldsymbol{W}_{O}, & r \in \mathcal{R} \\
\boldsymbol{W}_{I}, & r \in \mathcal{R}_{i n v} \\
\boldsymbol{W}_{S}, & r=\top(\text { self-loop })
\end{array}\right.
$$
在该模式下, 一些以前的方法能够被纳入CompGCN的框架之中:
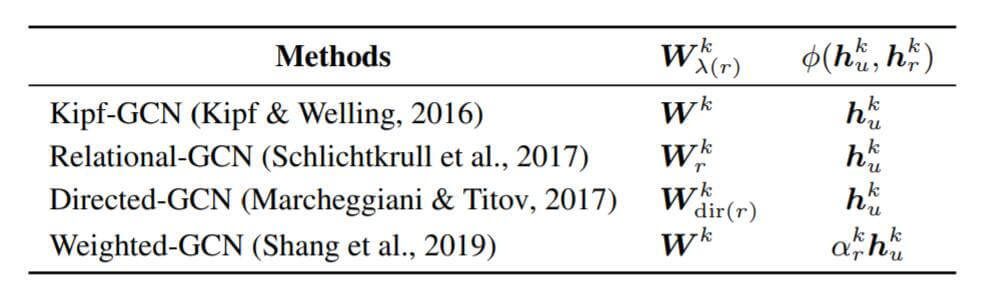
从CompGCN的身上能偶找到这些过去方法的影子.
关系嵌入同节点嵌入的聚合一样, 也需要做类似的更新, 但关系没有邻居之类的概念, 直接用简单的投影即可:
$$
\boldsymbol{h}_{r}=\boldsymbol{W}_{\mathrm{rel}} \boldsymbol{z}_{r}
$$
$\boldsymbol{W_{\text{rel}}}$ 是与关系无关的变换矩阵, 它只是将初始关系嵌入$\boldsymbol{z}_{r}$ 投影到关系嵌入空间而已.
与R - GCN一样, CompGCN也使用基函数分解来减轻GCN的过参数化. 但用途仅为获得初始化的关系嵌入$\boldsymbol{z}_r$:
$$
\boldsymbol{z}_{r}=\sum_{b=1}^{\mathcal{B}} \alpha_{b r} \boldsymbol{v}_{b}
$$
基函数分解并没有在后续更新关系(边)的Embedding中使用到.
上述为CompGCN在只有一层情况下的说明.
CompGCN in Multilayer
对于多层的情况, 只需要将上面的方程改写为含有层数$k$ 的形式:
$$
\boldsymbol{h}_{v}^{k+1}=f\left(\sum_{(u, r) \in \mathcal{N}(v)} \boldsymbol{W}_{\lambda(r)}^{k} \phi\left(\boldsymbol{h}_{u}^{k}, \boldsymbol{h}_{r}^{k}\right)\right)
$$
关系表示$\boldsymbol{h}_r^k$ 的更新也按照多层形式写出:
$$
\boldsymbol{h}_{r}^{k+1}=\boldsymbol{W}_{\mathrm{rel}}^{k} \boldsymbol{h}_{r}^{k}
$$
注意, $\boldsymbol{W}_{\text{rel}}$ 每层参数都是不同的, 多层GCN也对关系嵌入多次迭代更新.
作者对比了CompGCN与普通GCN方法的优势:

$K$ 为GCN的层数, $d$ 为Embedding维度, $\mathcal{B}$ 为基的数量, $\lvert \mathcal{R} \rvert$ 为关系个数.
CompGCN复杂度中的第一项来自于与层数相关的$\boldsymbol{W}_{\text{rel}}, \boldsymbol{W}_{\lambda(r)}$, 第二, 三项分别来自于基函数分解中的基$\boldsymbol{v}_{b}$ 和标量$\alpha_{b r}$.
相较于其他的GCN算法, 尤其是R - GCN, CompGCN保持了相对少的参数量.
Experiments
详细的实验参数设置请参照原论文.
Link Prediction
CompGCN在链接预测上的玩法仍然沿用了R - GCN中Encoder - Decoder的架构
R - GCN使用的Decoder是DistMult, 解码时关系嵌入需要额外训练, 并且存在实体嵌入和关系嵌入的方法不匹配问题, 这就割裂了实体嵌入和关系嵌入的关系. 但CompGCN在编码阶段就引入了关系嵌入, 不会存在关系和实体嵌入训练不匹配的问题:
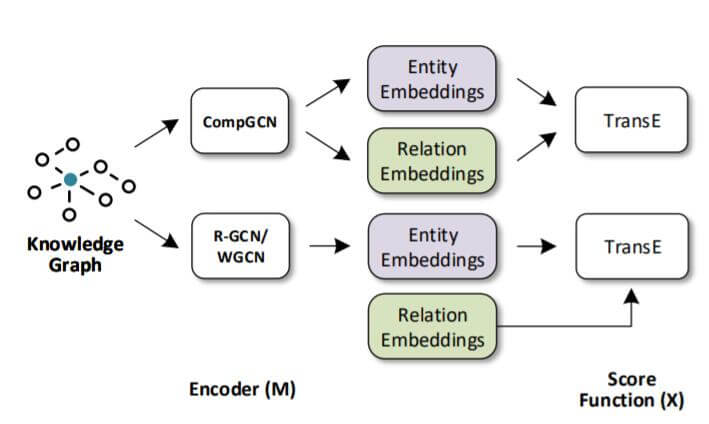
Main Result
作者在FB15k - 237和WN18RR上做了Link Prediction, 结果如下:
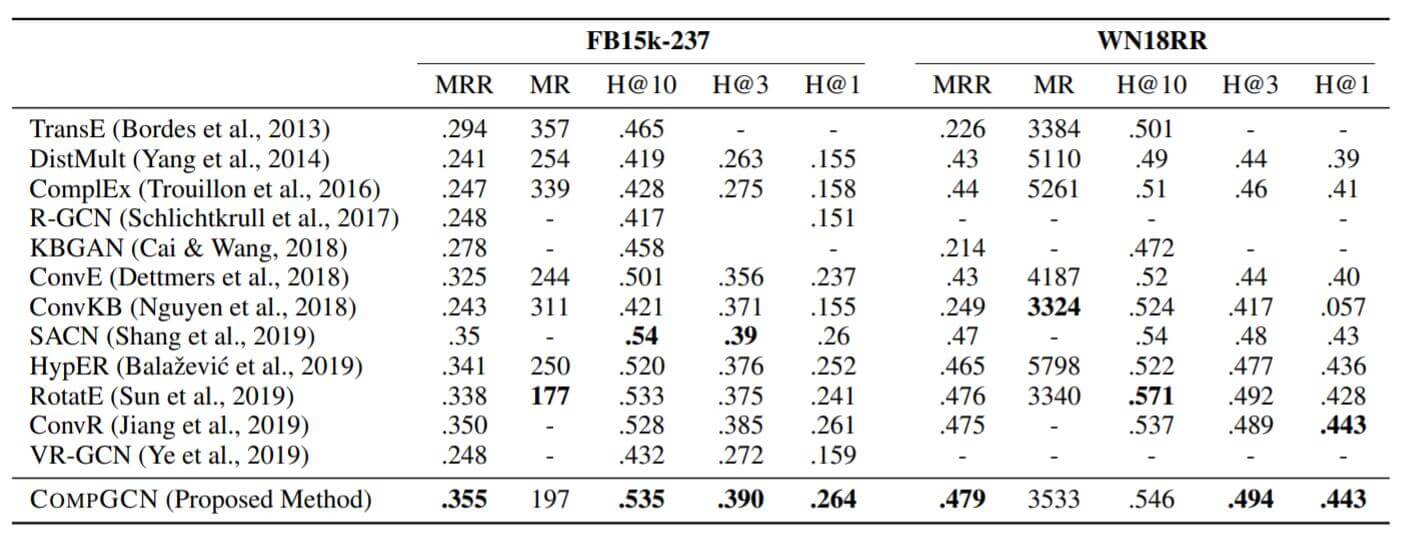
无论是比传统的KGE方法, 还是其他基于图的KGE方法, CompGCN的综合表现比较不错, 在WN18RR上的Hits@10比RotatE少了三个点.
Comparison in CompGCN
作者主要比较了不同GCN方法在不同Decoder下的链接预测性能表现, 其形式为$\mathbf{X}+\mathbf{M}(\mathbf{Y})$, $\mathbf{X}$ 代表某种KGE方法的打分函数, $\mathbf{M}$ 代表用来获取实体和关系Embedding的GCN方法名称, $\mathbf{Y}$ 代表组合操作符.
在FB15k - 237上的结果如下:
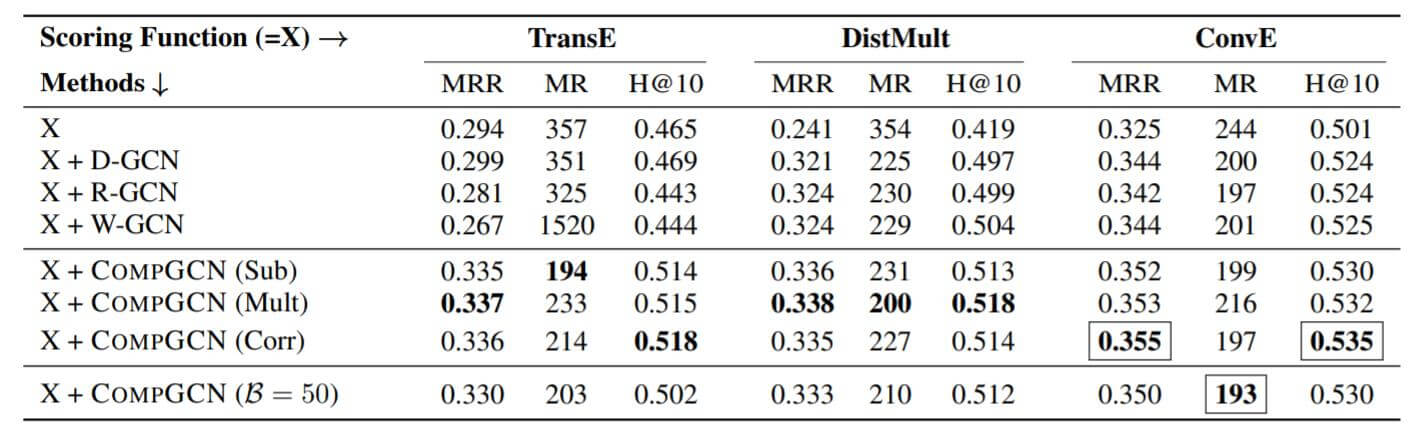
几乎所有的GCN方法会导致TransE的性能退化, 但CompGCN没有. 可能因为关系和实体的联合学习. 不同的组合操作所擅长的优化指标是不相同的.
Scalability of CompGCN
Effect of Varying Relation Basis Vectors
作者比较了FB15k - 237上不同基向量个数对相对MRR的影响:
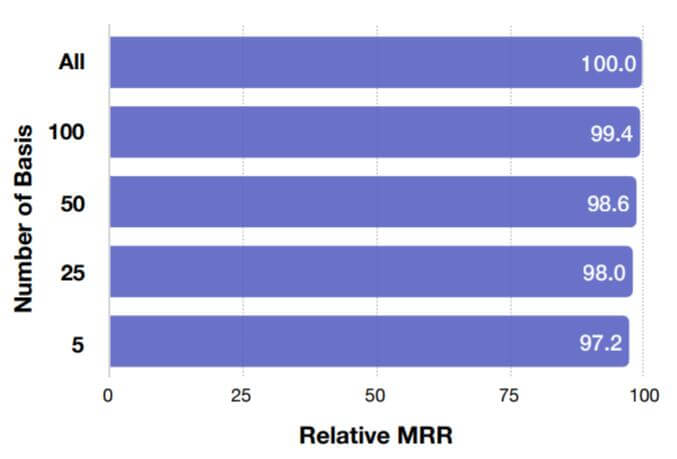
当基向量个数为237, 即关系不使用基向量时性能达到最好. 但采用更少的基向量并不会带来非常明显的性能衰减.
Effect of Number of Relations
作者比较了FB15k - 237中, 对于相同的基函数为5的情况下, 不同关系数量上的相对MRR:
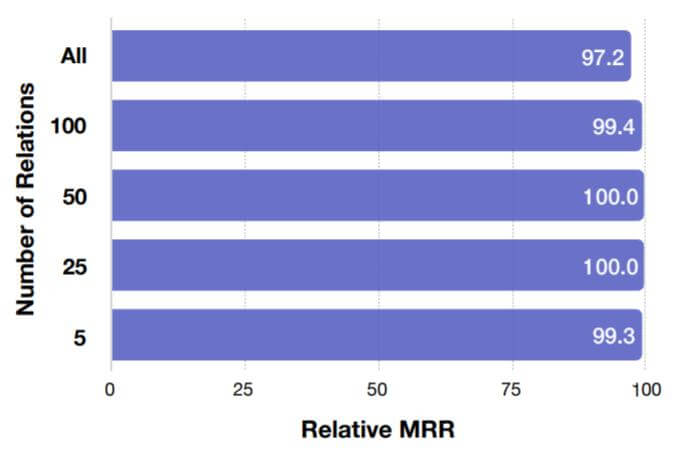
即使固定基函数为5, 仍然能比较好的应对繁多的关系.
上述两个实验说明关系之间可能存在着大量线性相关, 少量的基向量完全可以重新组合表示它们.
Comparison with R - GCN
作者对比了R - GCN和CompGCN在FB15k - 237的不同关系数量子集中的表现:
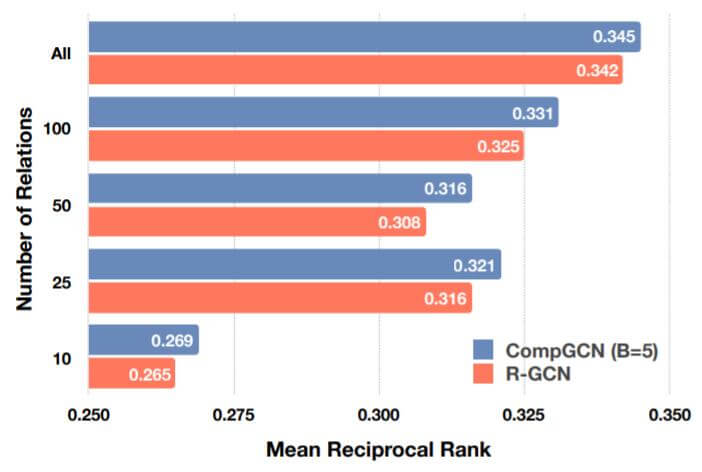
仅仅在5个基函数的情况下, CompGCN全面优于R - GCN.
Node and Graph Classification
在节点和图分类任务中, CompGCN表现如下:
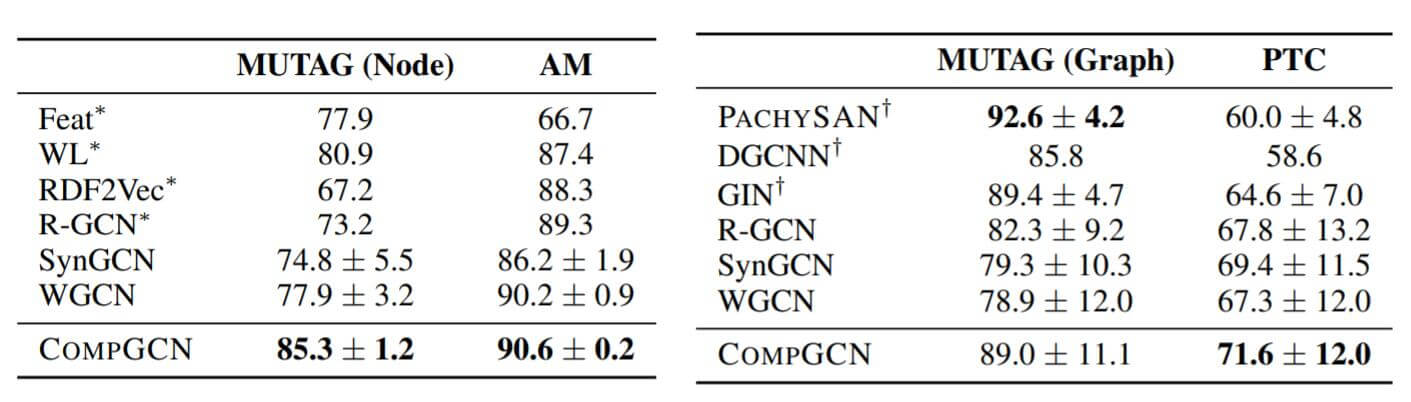
这两个数据集上, 对于简单的节点分类和图分类问题, CompGCN表现良好.
Summary
CompGCN进一步地将Knowledge Embedding中对待关系的方法引入了GCN领域, 在之前的GCN类方法中, 常不将关系嵌入引入, 而在KGE领域中, 将关系和实体嵌入共同使用是非常普遍的.
CompGCN算是集大成者, 作者考虑了很多关于GCN过参数化的内容. 同时兼顾有向, 多关系, 支持关系嵌入三种特性.
作者着重论述了CompGCN的各方面优势, 例如复杂度, 可扩展性, 以及具体任务的性能等.
作者在文中使用的是非参数化的组合方式, 其实也可以尝试参数化的组合, 这样也会引入更高的复杂度.
作者也没有考虑引入Attention来增强边对节点的影响, 而是使用了对边类型的特化来处理, 可能Attention的泛用性更强一些.

