本文前置知识:
- GNN: 详见图神经网络入门
Modeling Relational Data with Graph Convolutional Networks
本文是论文Modeling Relational Data with Graph Convolutional Networks的阅读笔记和个人理解.
Basic Idea
大规模知识图谱仍然不完整, 并且知识图谱中还没有针对图结构建模的方法, 而节点缺失的信息经常可以由邻居编码而来.
在KG中, 经常以Entity Classification和Link Prediction作为任务来衡量模型对KG补全的能力:
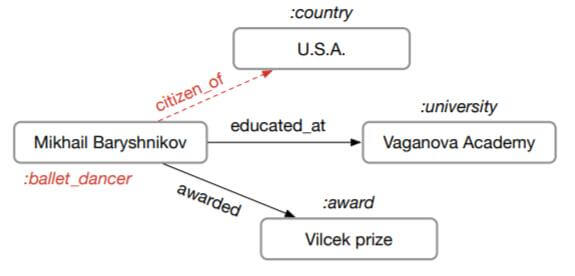
图中红色字体为缺失信息, 对应着实体类型和关系.
在大规模知识图谱中, 多关系数据特性十分显著, 作者希望针对多关系数据, 提出一种基于图的方法处理知识图谱补全问题.
R - GCN
有向且有标签的多图被表示为$G=(\mathcal{V, E, R})$, 其中节点$v_i \in \mathcal{V}$, 边$(v_i, r, v_j) \in \mathcal{E}$, 关系类型$r \in \mathcal{R}$.
Relational Graph Conovlutional Network
R - GCN是一种GCN的扩展形式, GCN能够聚合周围邻居的信息.
GCN遵循消息传递机制:
$$
h_{i}^{(l+1)}=\sigma\left(\sum_{m \in \mathcal{M}_{i}} g_{m}\left(h_{i}^{(l)}, h_{j}^{(l)}\right)\right)
$$
其中$h_{i}^{(l)}$ 是节点$v_i$ 第$l$ 层的隐藏状态, $\mathcal{M_i}$ 为节点$v_i$ 的入边. $\sigma$ 为非线性激活函数, 例如$\operatorname{ReLU}$.
$g_m(\cdot, \cdot)$ 为邻居节点的聚合方式, 一般只用简单的线性变换作为替代, 即$g_m(h_i, h_j) = Wh_j$.
这部分有问题请参见图神经网络入门中的GCN和消息传递部分.
R - GCN针对不同种类的关系进行了特化处理, 即针对不同的关系采用不同的聚合方式, 在这里是使用了不同的线性变换矩阵$W_r$. 其更新方程为:
$$
h_{i}^{(l+1)}=\sigma\left(\sum_{r \in \mathcal{R}} \sum_{j \in \mathcal{N}_{i}^{r}} \frac{1}{c_{i, r}} W_{r}^{(l)} h_{j}^{(l)}+W_{0}^{(l)} h_{i}^{(l)}\right)
$$
其中$c_{i, r}$ 代表归一化因子, 可以由学习得来, 或规定$c_{i, r} = |\mathcal{N}_i^r|$. $W_0$ 代表节点自身闭环所对应的变换矩阵.
针对节点$v_i$ 及其所有邻居$\mathcal{N_i}$, 分别考虑$v_i$ 与邻居$v_j$ 二者之间的关系$r$, 施加以不同的关系变换$W_r$, 再将它们求和并归一化, 加上自身的闭环影响, 在激活函数的影响下获得下一层的节点表示.
对于有向异质图(有向多关系图), R - GCN每个节点表示的更新方式大致可以由下图描述:
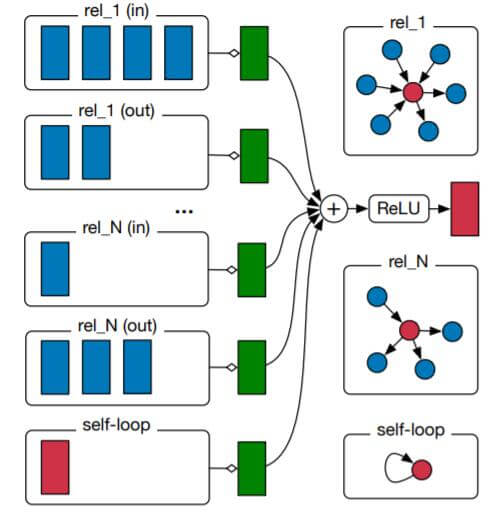
蓝色块对应着不同关系下蓝色的不同邻居对红色中心节点的影响, 每种关系分别经过变换求和得到绿色块, 对所有关系的绿色块求和并激活, 得到红色中心节点的新表示.
同一类型关系的不同指向被视为不同关系(同关系下的出入被视为是不同的).
对于关系非常多的图, 每一种关系都对应着一个独特的变换矩阵, 参数量将是巨大的, 增加了潜在的过拟合风险.
Regularization
针对上小节图神经网络过参数化的问题, 作者提出两种减少参数从而减轻过拟合的方法. 分别是基函数分解和对角块分解.
Basic Decomposition
基函数分解将所有关系的权重矩阵视为不同系数和基的线性组合:
$$
W_{r}^{(l)}=\sum_{b=1}^{B} a_{r b}^{(l)} V_{b}^{(l)}
$$
其中$B$ 为基的数量, $a_{rb}$ 是不同关系$r$ 下的系数, $V_b$ 是线性基.
这种表示方法可以被视为是不同关系下的权重共享, 对于少关系的情况能够缓解过拟合现象, 因为关系之间的基是相互共享的, 基总会被其他关系所频繁更新.
Block - Diagonal Decomposition
对角块分解将变换矩阵$W_r$ 拆分为$B$ 个大小相同的块:
$$
W_{r}^{(l)}=\bigoplus_{b=1}^{B} Q_{b r}^{(l)}
$$
其中$Q_{b r}^{(l)} \in \mathbb{R}^{\left(d^{(l+1)} / B\right) \times\left(d^{(l)} / B\right)}$, $\bigoplus$ 为生成对角阵的操作$\operatorname{diag}$.
对角块分解又可以视为是一种$W_r$ 的一种稀疏性约束, 除去块的位置其余位置都是0, 与未分解时相比更为稀疏. 而且由于分块的影响, 在每个块内部, 隐特征的联系将比块与块之间更加紧密.
至此, R - GCN已经能够作为一个单独的层, 按照层级结构堆叠获得$L$ 层的多层输出. 如果没有节点的初始特征, 可以采用Embedding的方式获取.
原文中说的独热 + 单层线性变换获取的稠密表示实际上就是Embedding.
Entity Classification
对于实体分类问题, R - GCN能直接将堆叠过后最后一层的节点输出作为Logits, 预测实体类别:
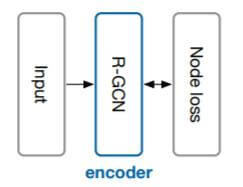
将最后一层的激活函数更换为$\operatorname{softmax}$, 接着最小化多分类交叉熵即可:
$$
\mathcal{L}=-\sum_{i \in \mathcal{Y}} \sum_{k=1}^{K} t_{i k} \ln h_{i k}^{(L)}
$$
其中$\mathcal{Y}$ 为有标签的节点集合, $K$ 为类别总数.
Link Prediction
对于链接预测问题, 通常在三元组$(s, r, o)$ 上(也就是边$\mathcal{E}$) 预测缺失的尾实体$o$. 但R - GCN只能根据某节点不同关系的邻居获得自身的表示, 并不能结合关系信息做尾实体的预测.
因此, 作者将R - GCN集成进Auto Encoder的框架, 将R - GCN视为一个获取所有节点编码的Encoder, 再用其他的KGE模型对节点(实体)表示打分, 以完成链接预测任务:
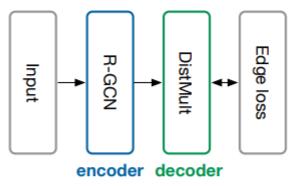
在这里, 作者选用DistMult作为Decoder. 其打分函数如下:
$$
f(s, r, o)=e_{s}^{T} R_{r} e_{o}
$$
DistMult是基于语义匹配的模型, 对每个不同的关系, DistMult都有不同的对角矩阵$R_r$ 来变换头实体$e_s$, 然后与尾实体$e_o$ 做相似度匹配. 所有的Embedding, $e_s, e_o$ 都来源于R - GCN.
DistMult虽然也对关系做了特化处理, 但只靠对角矩阵做变换显然是无法应对多元化关系的.
所以R - GCN的在链接预测上的性能可能受到了约束.
然后用BCE作为损失函数优化:
$$
\mathcal{L}=-\frac{1}{(1+\omega)|\hat{\mathcal{E}}|} \sum_{(s, r, o, y) \in \mathcal{T}} y \log l(f(s, r, o))+
(1-y) \log (1-l(f(s, r, o)))
$$
其中$\omega$ 代表每个正样本采样多少个负样本. $l$ 为$\operatorname{sigmoid}$ 函数.
Experiments
详细的超参数设置和Trick请参照原论文.
Entity Classification Experiments
作者分别在四个实体分类数据集AIFB, MUTAG, BGS, AM上进行了实体分类任务, 数据集的统计信息如下:
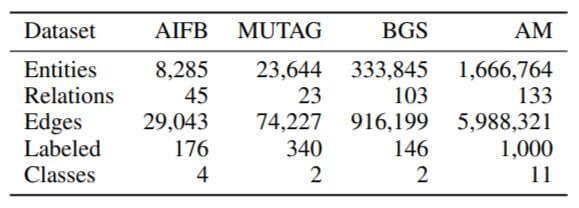
实验结果如下:
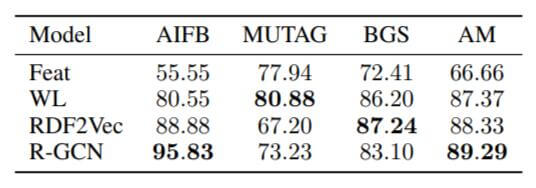
在AIFB和AM上的效果都要高于其他模型, 而MUTAG和BGS是特定领域的数据集, 与其他两个数据集都不太一样, 导致了R - GCN的性能差距.
作者提到, 对所有邻居都采用相同权重的归一化方式可能会有损性能, 一种潜在的解决方案是采用注意力机制, 通过学习分配给周围邻居不同的权重.
其实就是同年10月份提出的GAT, 而R - GCN发布于同年3月份.
Link Prediction Experiments
作者主要在FB15k, WN18, FB15k - 237上做了链接预测的实验.
同样是针对关系特化的模型, 作者做出了在FB15k的验证集中不同度对MRR的影响曲线:
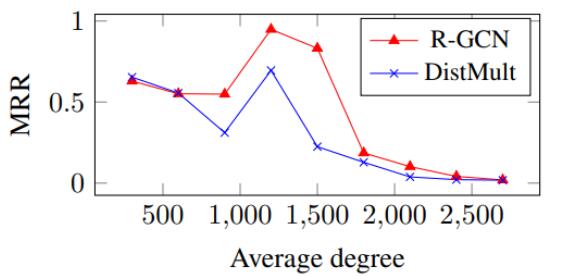
作者认为R - GCN在度比较高, 即上下文信息比较多时处理很占优势, 而DistMult在度比较低时占优势.
可能也只是作者的一个推测, DistMult在度比较低的时候并没有比R - GCN好特别多.
观察到R - GCN和DistMult上的互补优势, 作者尝试将两种模型融合, 仍然采用DistMult的打分函数, 但Embedding分别来自于已经训练好的不同模型:
$$
f(s, r, t)_{\mathrm{R}-\mathrm{GCN}+}=\alpha f(s, r, t)_{\mathrm{R}-\mathrm{GCN}}+(1-\alpha) f(s, r, t)_{\text {DistMult }}
$$
$\alpha$ 为选择模型得分的权重. 在FB15k中设置为$\alpha=0.4$, 即来自DistMult的打分要多一些, R - GCN少一些, 因为作者不希望改进后的模型性能显著高于纯R - GCN.
在FB15k, WN18上结果如下:
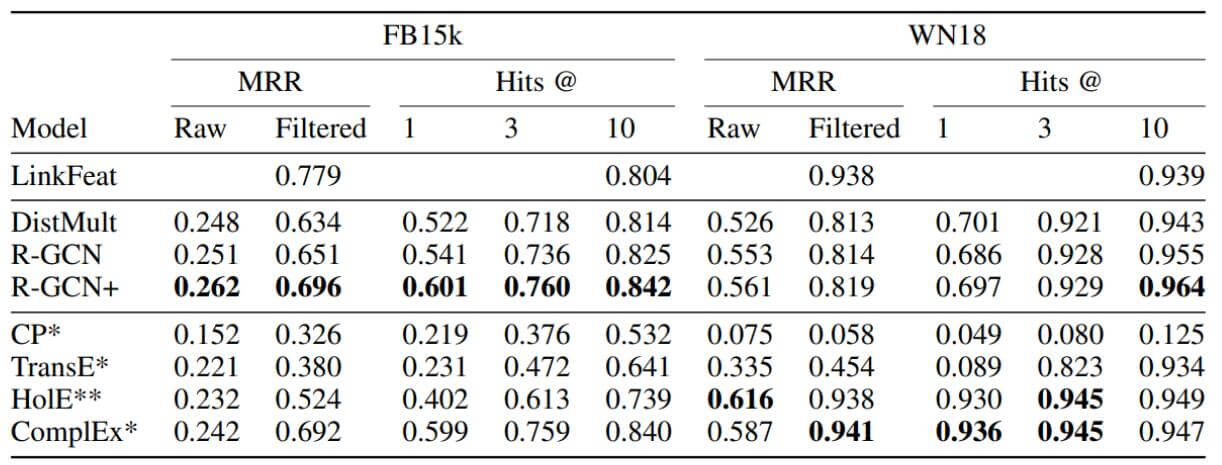
在关系比较少的WN18上, R - GCN并不占优势, 但在FB15k上的表现十分不错. DistMult作为关系特化的模型也在FB15k上显示出一些优势, 但仍不及能够对对称, 反对称, 逆关系同时建模的ComplEx.
在FB15k - 237上结果如下:
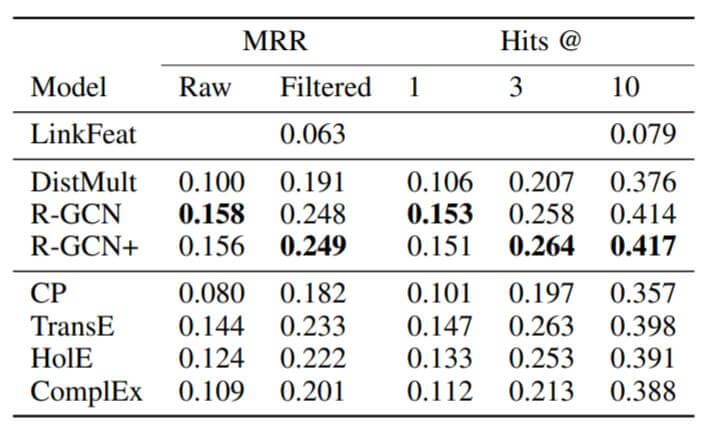
R - GCN比其他方法效果要好特别多, 因为把DistMult也塞进去了, 所以比DistMult也显著的好.
Summary
R - GCN是一篇比较早的GNN论文, 已经作为一种KGE中常用的图方法Baseline出现, 也正是R - GCN使得大家对图方法在KG上的应用提起了注意.
R - GCN在GCN的基础上对多关系进行特化, 并针对图神经网络的过拟合问题提出了两种可替代的解决方法, 基函数分解和对角块分解. 也提出了图神经网络在处理Entity Classification和Link Prediction问题上的框架, 其实主要还是把R - GCN的输出作为一种Node Embedding的方法来使用.
作者在文中还提出了两种可以优化的地方:
- Decoder还可以替换为任意的KGE模型, 例如能对更多关系建模的ComplEx.
- 对邻居节点的权重分配可以通过Attention学习得来.

