本文前置知识:
- GAT: 详见图神经网络入门.
Learning Attention-based Embeddings for Relation Prediction in Knowledge Graphs
本文是论文Learning Attention-based Embeddings for Relation Prediction in Knowledge Graphs的阅读笔记和个人理解.
Basic Idea
作者观察到, 虽然基于CNN的模型能生成关于三元组更丰富的信息, 但处理三元组时是独立的, 并没有覆盖周围邻居的复杂信息. 现有的方法要么只关注实体特征, 要么不会对实体和关系的特征共同嵌入.
作者希望利用Attention机制来共同捕捉节点与邻居的实体和关系特征.
KBAT
Graph Attention Network
这部分对GAT有基础的可以直接跳过, 作者在原论文中描述GAT的式子与GAT本身论文中没区别.
对于有$N$ 个节点的图, 输入节点特征为$\mathbf{x}=\left\{\vec{x}_{1}, \vec{x}_{2}, \ldots, \vec{x}_{N}\right\}$, 在经过一层GNN变换后, 节点特征被更新为$\mathbf{x}^{\prime}=\left\{\vec{x}_{1}^{\prime}, \vec{x}_{2}^{\prime}, \ldots, \vec{x}_{N}^{\prime}\right\}$.
在注意力机制中, 边$(e_i, e_j)$ 的注意力值$e_{ij}$ 由下式决定:
$$
e_{i j}=a\left(\mathbf{W} \overrightarrow{x_{i}}, \mathbf{W} \overrightarrow{x_{j}}\right)
$$
$\mathbf{W}$ 为线性变换矩阵, 能将节点特征投影到更高的维度, $a$ 是可选择的Attention Function.
在更新节点隐态信息时, 将在GCN的基础上对节点的邻居加权聚合:
$$
\overrightarrow{x_{i}^{\prime}}=\sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j} \mathbf{W} \overrightarrow{x_{j}}\right)
$$
$\alpha_{ij}$ 是用Softmax对节点$i$ 所有邻居$j$ 的注意力值由$e_{ij}$ 计算得到的注意力权重.
与Transformer类似, GAT中引入了多头注意力, 更新方程如下:
$$
\overrightarrow{x_{i}^{\prime}}=\lVert_{k=1}^{K} \sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j}^{k} \mathbf{W}^{k} \overrightarrow{x_{j}}\right)
$$
$\lVert$ 代表Concat操作, $\sigma$ 为非线性函数, $K$ 代表多头的头数. $\alpha_{ij}^k$ 代表第$k$ 个头内归一化的注意力权重, $\mathbf{W}^k$ 是第$k$ 个头的线性变换矩阵.
最后一层将GAT输出作为Embedding, 将多头的信息通过平均的方式整合:
$$
\overrightarrow{x_{i}^{\prime}}=\sigma\left(\frac{1}{K} \sum_{k=1}^{K} \sum_{j \in \mathcal{N}_{i}} \alpha_{i j}^{k} \mathbf{W}^{k} \overrightarrow{x_{j}}\right)
$$
Relations are Important
在KG中, 相同的实体在不同关系的作用下意义会变得完全不一样, 所以关系嵌入是非常重要的.
例如, 在下述场景中, Christopher Nolan出现在了两个不同的三元组中, 所对应的关系分别是directed和brother_of, 他的身份分别是导演和哥哥:
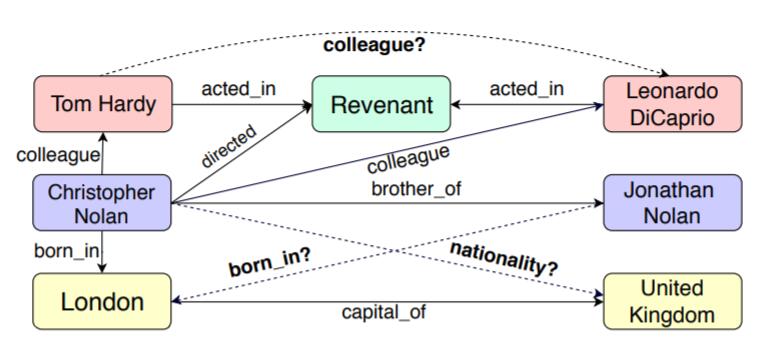
因此, 在将GAT引入KGE时, 必须将关系嵌入也一并纳入注意力的计算范畴.
在每层GAT中, $\mathbf{H}, \mathbf{G}$ 分别代表输入时实体嵌入和关系嵌入矩阵. $\mathbf{H}^\prime, \mathbf{G}^\prime$ 为输出时实体嵌入, 关系嵌入矩阵. 特别定义$t_{ij}^k=(e_i, r_k, e_j)$ 为三元组.
我们从输入实体嵌入矩阵$\mathbf{H}$ 中取出实体表示$\vec{h_i}, \vec{h_j}$, 从输入关系嵌入矩阵$\mathbf{G}$ 中取出关系表示$\vec{g_k}$, 获取三元组$t_{ij}^k$ 整体在嵌入空间中的表示$\vec{c_{i j k}}$:
$$
\vec{c_{i j k}}=\mathbf{W}_{1}\left[\vec{h}_{i}\lVert\vec{h}_{j}\lVert \vec{g}_{k}\right]
$$
$\mathbf{W}_1$ 为线性变换矩阵.
然后利用整体表示再次经过变换, 对$c_{ijk}$ 变换后用LeakyReLU过滤得到Attention Score $b_{ijk}$:
$$
b_{i j k}=\operatorname{LeakyReLU}\left(\mathbf{W}_{2} c_{i j k}\right)
$$
$\mathbf{W}_2$ 是线性变换矩阵.
根据Attention Score, 用Softmax可以得出三元组的Attention Weight $\alpha_{ijk}$:
$$
\begin{aligned}
\alpha_{i j k} &=\operatorname{softmax}_{j k}\left(b_{i j k}\right) \\
&=\frac{\exp \left(b_{i j k}\right)}{\sum_{n \in \mathcal{N}_{i}} \sum_{r \in \mathcal{R}_{i n}} \exp \left(b_{i n r}\right)}
\end{aligned}
$$
$\mathcal{N}_i$ 代表节点$i$ 的邻居节点集, $\mathcal{R}_{in}$ 代表节点$i$ 与邻居$n$ 之间的关系集.
因此, KBAT的前半部分与GAT相比, 只是把关系嵌入$g_k$ 塞进了GAT中:
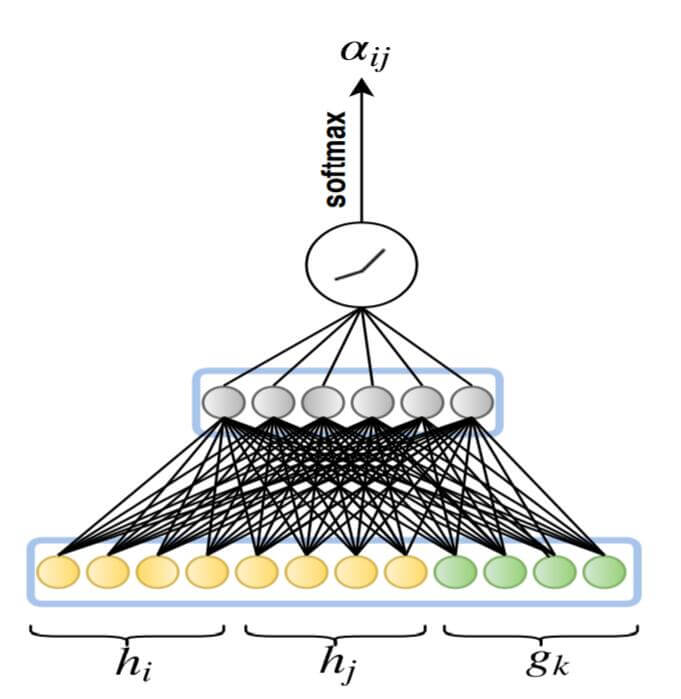
在更新节点表示时, 对实体$i$ 为头实体的三元组$\vec{c_{ijk}}$ 加权求和得到新的节点表示:
$$
\overrightarrow{h_{i}^{\prime}}=\sigma\left(\sum_{j \in \mathcal{N}_{i}} \sum_{k \in \mathcal{R}_{i j}} \alpha_{i j k} \vec{c_{i j k}}\right)
$$
和GAT相同, 也可以采用多头注意力的方式来增强GAT的稳定性:
$$
\overrightarrow{h_{i}^{\prime}}=\lVert_{m=1}^{M} \sigma\left(\sum_{j \in \mathcal{N}_{i}} \alpha_{i j k}^{m} c_{i j k}^{m}\right)
$$
其中$\lVert$ 代表Concat操作, $M$ 为注意力头数.
我们已经获取了实体在单层GAT的更新后的表示, 也需要对关系做一些改变, 保证节点嵌入更新的同时, 关系嵌入也是在更新的:
$$
G^{\prime}=G \cdot \mathbf{W}^{R}
$$
$\mathbf{W}^R$ 是权重矩阵, 可以改变关系嵌入的维度.
Final Output Layer
在最终KBAT输出时, 需要聚合多头注意力的信息, 并对节点表示做进一步处理.
输出节点表示时, 与GAT类似, 将多个头的信息直接求平均聚合作为节点表示:
$$
\overrightarrow{h_{i}^{\prime}}=\sigma\left(\frac{1}{M} \sum_{m=1}^{M} \sum_{j \in \mathcal{N}_{i}} \sum_{k \in \mathcal{R}_{i j}} \alpha_{i j k}^{m} c_{i j k}^{m}\right)
$$
但是初始信息可能会随着提取特征而丢失, 作者在最终的输出前把初始节点嵌入$\mathbf{H}^t$ 再加回来:
$$
\mathbf{H}^{\prime \prime}=\mathbf{W}^{E} \mathbf{H}^{t}+\mathbf{H}^{f}
$$
$\mathbf{W}^E$ 是为了让维度能够匹配的变换矩阵, $\mathbf{H}^f$ 为最终层前的KBAT节点表示输出.
其实就是类似残差的方法, 但是在原论文中却对残差只字未提.
至此, 整个KBAT的运算过程如下:
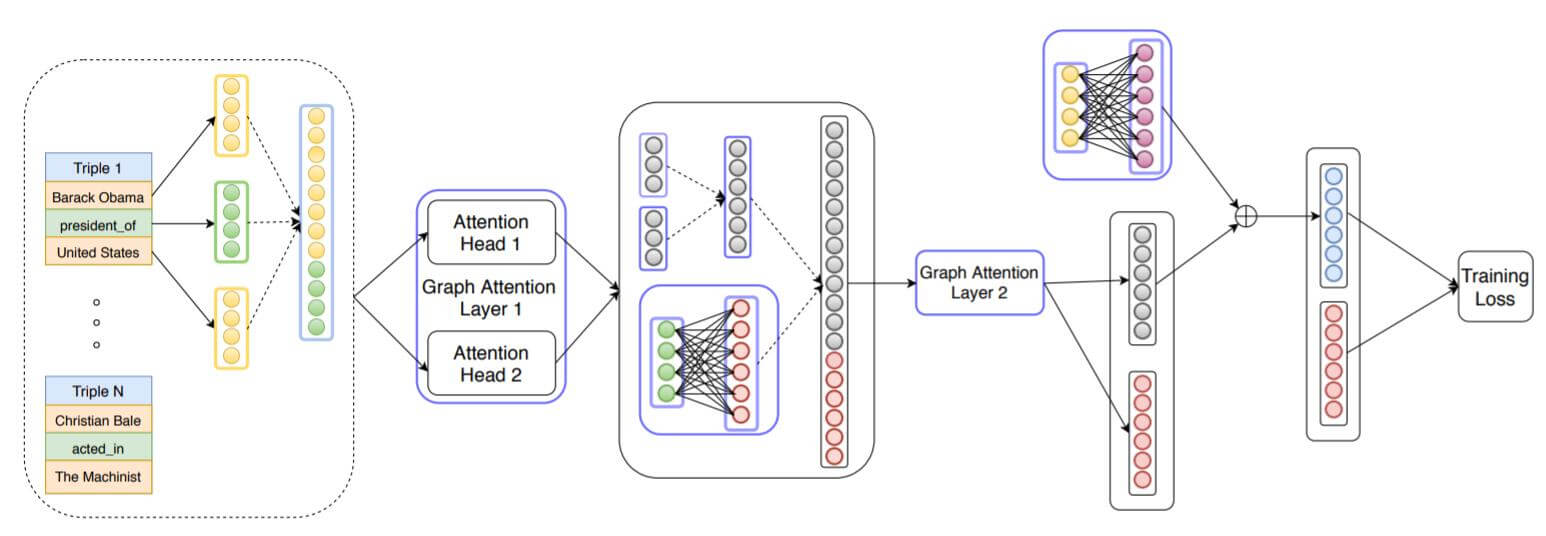
图中绿色圆圈为关系嵌入, 黄色圆圈为实体嵌入. 对图中的流程总结描述如下:
- 先将头实体, 尾实体, 关系的嵌入拼接起来.
- 经过GAT层的多头注意力后得到两个实体更新后的表示, 同时将关系嵌入做一次更新.
- 在下个GAT层前, 将更新后的头实体, 尾实体, 关系表示拼接起来.
- 再次经过GAT层. 得到两个实体的输出.
- 将最初的实体嵌入通过一次投影到与最终输出维度相匹配的维度, 和GAT输出的实体表示相加.
- 利用关系嵌入和实体嵌入共同计算Loss.
最后, 作者谈了一下多层GAT能够聚合N阶邻居信息的优势:
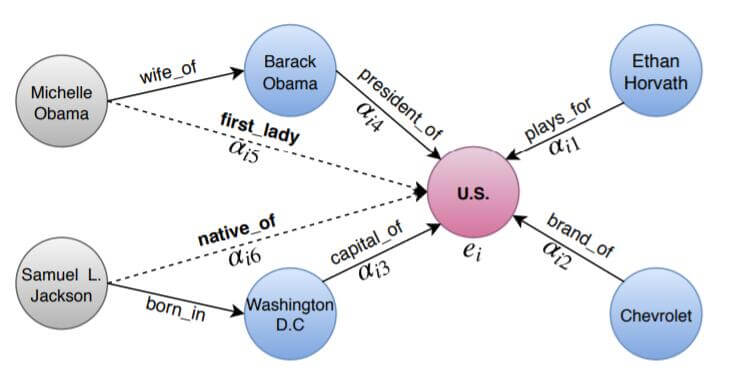
在图中, 多阶邻居的信息能够以多次迭代的方式被有可能相关联的实体所捕捉.
这种优势也只来自于GAT本身, 并不是由于KBAT的特殊性.
Training Objective
训练目标和TransE完全一致, 损失函数采用Hinge Loss:
$$
L(\Omega)=\sum_{t_{i j} \in S} \sum_{t_{i j}^{\prime} \in S^{\prime}} \max \left\{d_{t_{i j}^{\prime}}-d_{t_{i j}}+\gamma, 0\right\}
$$
$\gamma$ 为间隔, 距离的度量函数采用TransE的一范数, 即$d_{t_{ij}} = \lVert \vec{h_i} + \vec{g_k} - \vec{h_j} \rVert_1$.
也同样使用了负采样, $S$ 为有效三元组, $S^\prime$ 为负样本三元组:
$$
S^{\prime}=\underbrace{\left\{t_{i^{\prime} j}^{k} \mid e_{i}^{\prime} \in \mathcal{E} \backslash e_{i}\right\}}_{\text {replace head entity }} \cup \underbrace{\left\{t_{i j^{\prime}}^{k} \mid e_{j}^{\prime} \in \mathcal{E} \backslash e_{j}\right\}}_{\text {replace tail entity }}
$$
Decoder
KBAT在做链接预测时仍然像其他图方法一样, 沿用了Encoder - Decoder架构.
作者的模型中使用ConvKB作为解码器, 作者的目标是使用卷积层捕获三元组$t_{ij}^k$ 的全局信息. ConvKB的打分函数如下:
$$
f\left(t_{i j}^{k}\right)=\left(\prod_{m=1}^{\Omega} \operatorname{ReLU}\left(\left[\vec{h}_{i}, \vec{g}_{k}, \vec{h}_{j}\right] \ast \omega^{m}\right)\right) \cdot \mathbf{W}
$$
其中$\omega^m$ 为第$m$ 个卷积核, $\Omega$ 为卷积核总数, $\ast$ 为卷积操作. $\mathbf{W}$ 代表获取最终三元组得分的线性变换矩阵.
然后用软间隔损失来优化ConvKB:
$$
\mathcal{L}=\sum_{t_{i j}^{k} \in\left\{S \cup S^{\prime}\right\}} \log \left(1+\exp \left(l_{t_{i j}^{k}} \cdot f\left(t_{i j}^{k}\right)\right)\right)+\frac{\lambda}{2}|\mathbf{W}|_{2}^{2} \\
\text { where } l_{t_{i j}^{k}}=\left\{\begin{array}{ll}
1 & \text { for } t_{i j}^{k} \in S \\
-1 & \text { for } t_{i j}^{k} \in S^{\prime}
\end{array}\right.
$$
Experiments
详细的参数设置请参照原论文.
这篇论文的实验结果有很大问题, 在文末的Summary里会提到.
Main Results
作者将训练过程分为两步:
- 先用Hinge Loss单独训练KBAT作为Encoder, 使得GAT有编码能力.
- 再用Soft Margin Loss训练ConvKB作为Decoder, 使得ConvKB有解码能力.
原文并没有说是KBAT和ConvKB联合训练还是单独训练ConvKB, 但在代码中是ConvKB直接加载了已经训练好的KBAT的Embedding, 然后继续训练. 也就是直接使用KBAT的Embedding当做ConvKB的Embedding初始化, 同时训练Embedding和ConvKB, 并没有对Embedding做冻结.
作者针对此问题有回复, 但我仍感觉这样做可能会把KBAT提取好的Embedding信息破坏掉, 而非在KBAT的基础上去找ConvKB的更优解.
作者在五个常用数据集做了链接预测实验, 统计信息如下:

在WN18RR和FB15k - 237上结果如下:
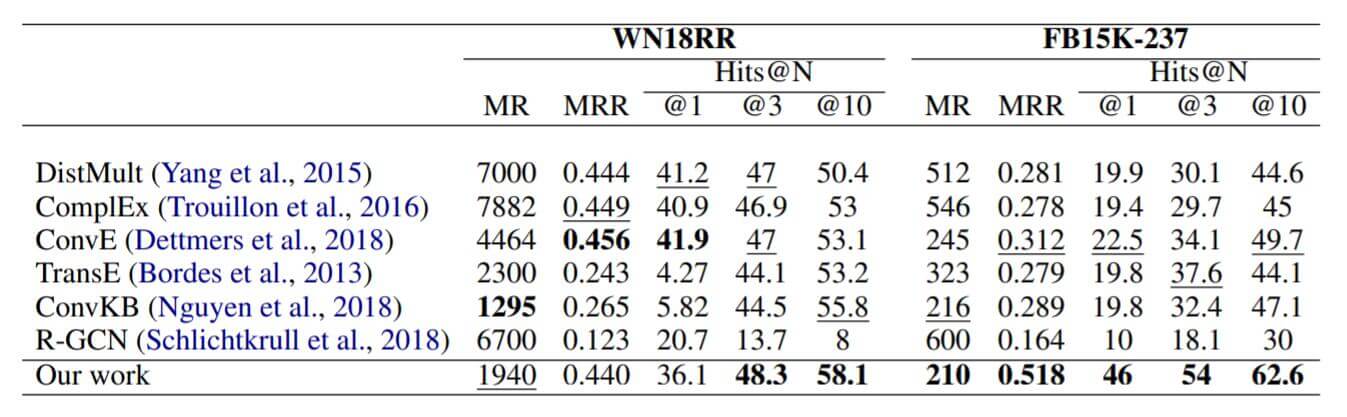
R - GCN在FB15k - 237和WN18RR上的结果没有超过ConvE, 但KBAT超过了. WN18RR上的Hits@1表现不太好. 作者在后面分析了原因.
在NELL - 995和Kinship上结果如下:
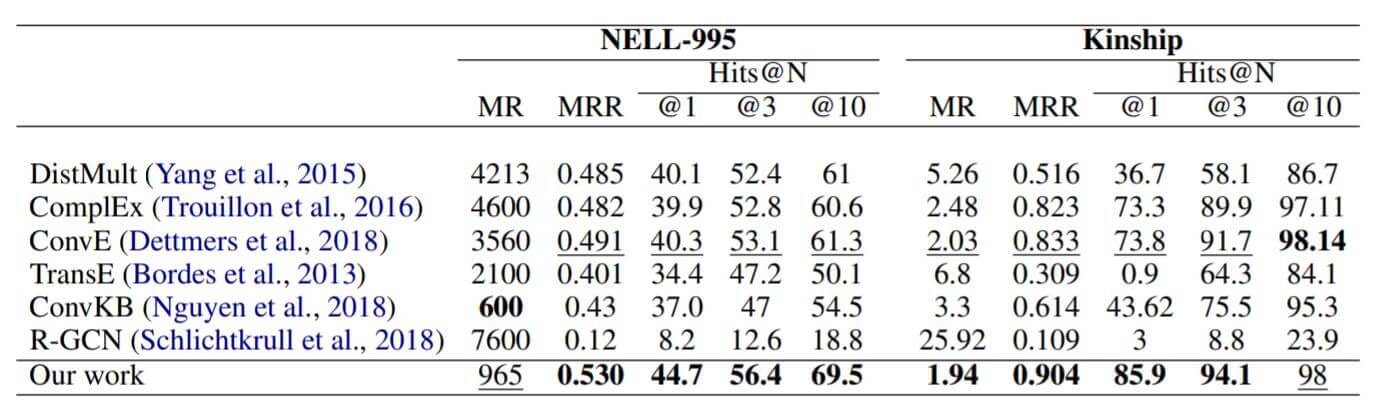
在这两个数据集上来看KBAT效果不错, R - GCN就不太行.
PageRank Analysis
作者假设复杂的多跳信息在稠密图中比在稀疏图中要更难捕获, 作者设计了类似ConvE中的实验, 探究了PageRank对模型的影响, 即测试将DistMult替换成KBAT后MRR的相对变化:
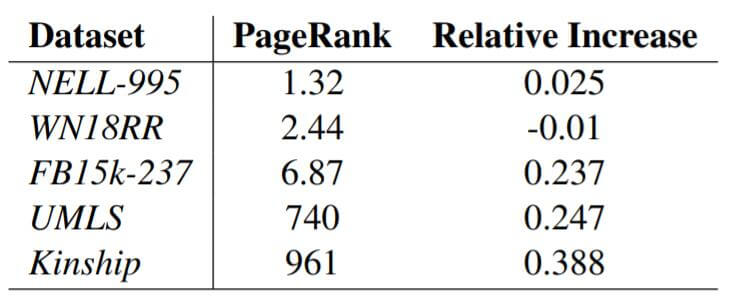
基本上PageRank越高, KBAT进步就越明显. 作者将在WN18RR上表现不好归因于WN18RR的高度稀疏和分级结构.
Attention Values vs Epochs
下图是FB15k - 237中注意力值随epoch增大的变化情况:
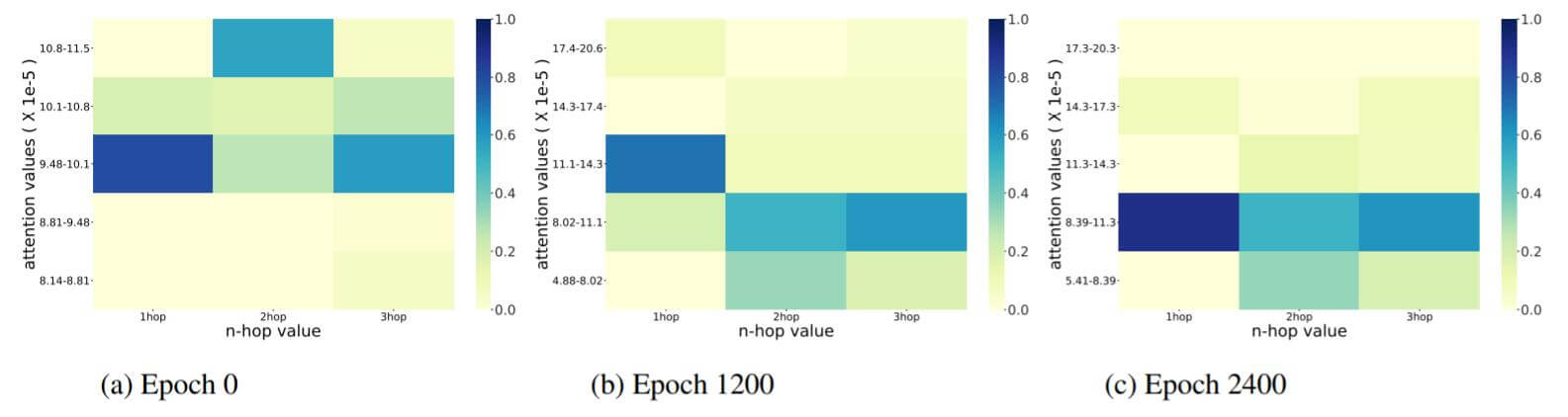
下图是WN18RR中注意力值随epoch增大的变化情况:
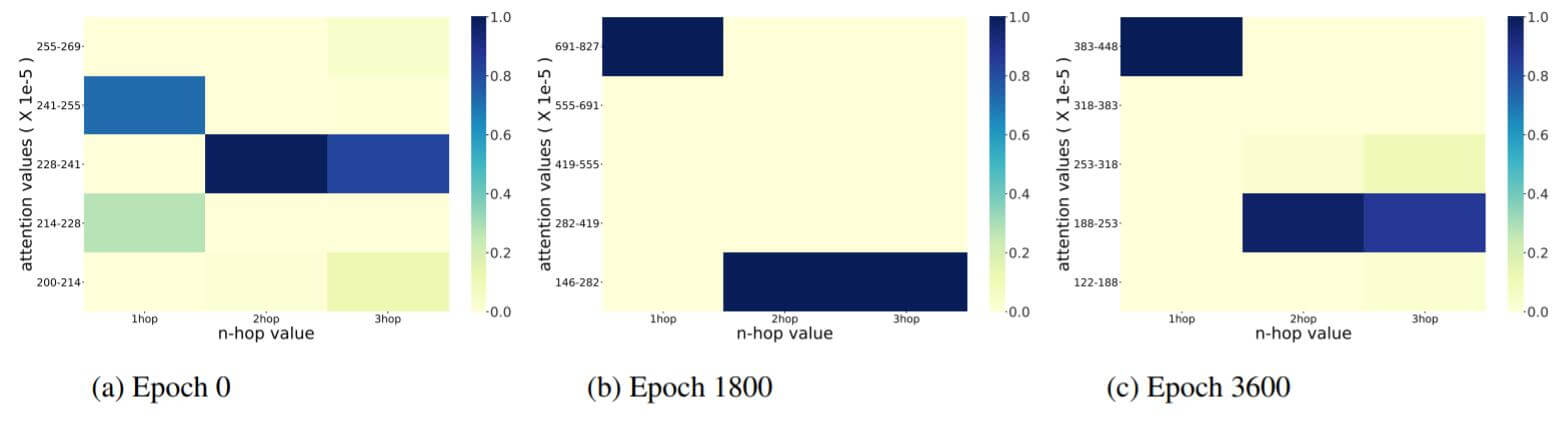
总体来说, 随epoch的增大, 多跳邻居会被分配给更多的注意力.
Ablation Study
作者逐渐移除模型中的信息, 做出NELL - 995上MR随epoch的变化曲线:
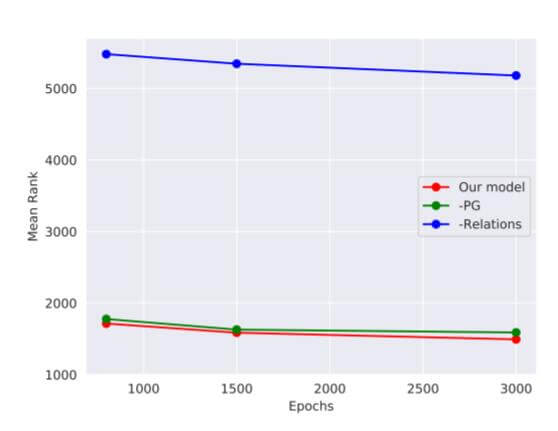
红色是作者的模型曲线, 绿色是移除多跳路径信息的曲线, 蓝色是移除关系信息的曲线.
作者也没说如何移除, 估计是用随机初始化来代替.
Summary
KBAT将GAT引入了KGE领域, 结合KG中的十分重要的关系, 利用图注意力网络的聚合特性, 获取实体之间的多跳信息, 并取得了比R - GCN更好的效果.
虽然有实验, 但是本论文除了将GAT引入KG领域中, 感觉没有什么创新点… 文中有很大篇幅都在介绍GAT. 有一些小改动也没有给出说明.
后续有一些论文说明KBAT给出的代码导致了Test Data存在Leakage, 详见此处, 所以实验结果大多站不住脚, 很多疑问都没有必要再追究了. 但使用GAT在思路上应该仍然有效.

