本文前置知识:
- ConvE
- Depth - wise Convolution
2020.11.14: 对实验进行部分补充.
InteractE: Improving Convolution-based Knowledge Graph Embeddings by Increasing Feature Interactions
本文章是论文InteractE: Improving Convolution-based Knowledge Graph Embeddings by Increasing Feature Interactions的阅读笔记和个人理解.
Basic Idea
Link Prediction能够根据已有的事实对缺失的链接进行推断, 依此缓解KG不完整的问题.
虽然已经有基于卷积的Embedding方法, 例如ConvE, ConvKB等, 但作者认为虽然卷积增加了头实体和关系之间的Embedding交互, 但交互次数仍然不够, 因此抽取特征的能力被限制了.
从名字上就能看出来, InteractE的主要思路就是通过一切手段让交互最大化, 从而实现更好的表达.
Definitions
Reshape Function
下面定义头实体和关系的$d$ 维Embedding分别为$\boldsymbol{e}_{s}=\left(a_{1}, \ldots, a_{d}\right), \boldsymbol{e}_{r}=\left(b_{1}, \ldots, b_{d}\right)$, 参数矩阵为$w$ 的卷积核大小为$k$, 并假设输入的矩阵$N$ 大小为$m \times n=2d$, 那么当卷积核对矩阵进行扫描时覆盖的区域$M_k$ 就应该有$M_k \subseteq N$, 且$M_k = N_{i:i+k, j:j+k}$. 我们将$\phi$ 记为Reshape Function, $\phi\left(\boldsymbol{e}_{s}, \boldsymbol{e}_{r}\right)$ 就代表了头实体和关系的Embedding后Reshape.
作者汇总了三种Reshape方法, 都非常好理解:
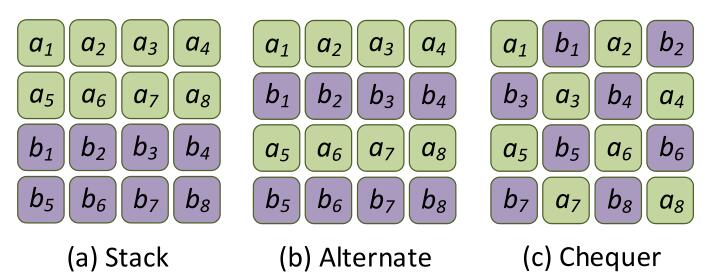
- Stack: 就是简单的堆叠, 这种方法被ConvE中使用, 记为$\phi_{s t k}$.
- Alternate: 将头实体和关系的Embedding按行交错排列, 记为$\phi_{a l t}^{\tau}$.
- Chequer(本文使用): 像棋盘一样的对二者的Embedding按元素交错排列, 即相邻的元素一定与自己的类型不同, 记为$\phi_{c h k}$.
Interaction
作者给出了交互精确的定义. 假设$M_{k} \subseteq \phi\left(\boldsymbol{e}_{s}, \boldsymbol{e}_{r}\right)$, $x,y$ 是$M_k$ 中的两个元素, 那么就能根据三元组$\left(x, y, M_{k}\right)$ 给出交互的定义.
如果$x,y$ 分别来自于$\boldsymbol{e}_{s},\boldsymbol{e}_{r}$, 则称该交互是异质(heterogeneous)的, 记为$\mathcal{N}_{h e t}(\phi, k)$. 反之, 如果来自于相同的Embedding, 则称该交互是同质(homogeneous)的, 记为$\mathcal{N}_{\text {homo}}(\phi, k)$.
对于Reshape Function $\phi$, 卷积核大小为$k$, 其中的元素交互次数定义为$\mathcal{N}(\phi, k)$, 如果有Padding, 可以将$\phi$ 替换为加上Padding的Reshape Function $\Omega(\phi)$.
下面用一个例子来说明交互的定义. 在一次$3\times 3$ 的卷积中, 子矩阵为$M_3$, 有5个元素来自$\boldsymbol{e}_{s}$, 4个元素来自$\boldsymbol{e}_{r}$. 那么异质交互的次数为:
$$
\mathcal{N}_{h e t}=2(5 \times 4)=40
$$
其中, $5\times 4$是来自$\boldsymbol{e}_{s}$ 和来自$\boldsymbol{e}_{r}$ 元素的组合次数, 前面的2代表每次组合相对两个元素分别有一次交互.
同理, 同质交互次数为:
$$
\mathcal{N}_{\text {homo}}=2\left[\left(\begin{array}{l}
5 \\
2
\end{array}\right)+\left(\begin{array}{l}
4 \\
2
\end{array}\right)\right]=32
$$
同质交互和异质交互的和是一个常数:
$$
\mathcal{N}_{h e t}(\phi, k)+\mathcal{N}_{h o m o}(\phi, k)=2\left(\begin{array}{c}
k^{2} \\
2
\end{array}\right)
$$
InteractE
Overview
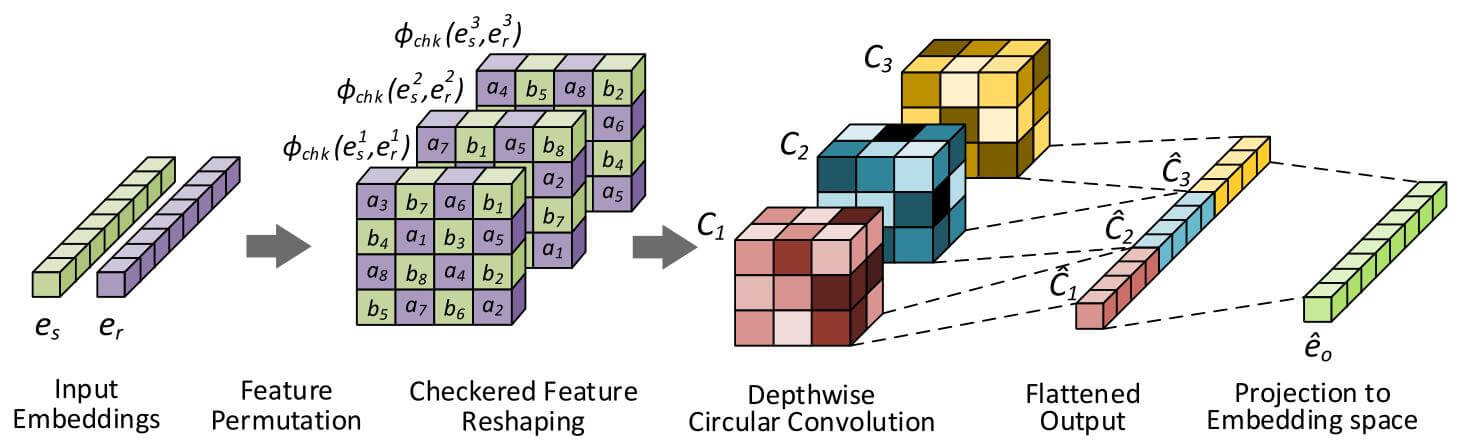
在ConvE的基础上, InteractE基于三种方式来最大化头实体与关系Embedding间的交互次数:
- Feature Permutation
- Checked Reshaping
- Circular Convolution
Details
Feature Permutation
InteractE使用随机排列的方式对头实体Embedding $e_s$ 和关系Embedding $e_r$ 打乱. 如果随机打乱$t$ 次, 那么结果集为$\mathcal{P}_{t}=\left[\left(e_{s}^{1}, e_{r}^{1}\right) ; \ldots ;\left(e_{s}^{t}, e_{r}^{t}\right)\right]$, 在Reshape后只是因为随机排列导致不同排列中对应位置的元素不同, 但仍然保证相邻两元素的类型不同, 记为$\phi\left(e_{s}^{i}, e_{r}^{i}\right)$.
通过多次随机排列, 能保证对Embedding上的每个Dim都是公平的.
Checkered Reshaping
$\phi_{chk}(\cdot)$ 能最大化异质交互次数, 我们对所有随机排列后的Embedding进行Reshape, 即:
$$
\phi\left(\mathcal{P}_{t}\right)=\left[\phi\left(e_{s}^{1}, e_{r}^{1}\right) ; \ldots ; \phi\left(e_{s}^{t}, e_{r}^{t}\right)\right]
$$
Circular Convolution
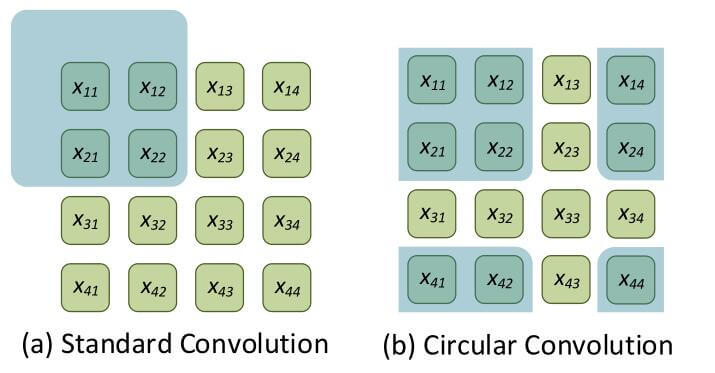
其实从图上来看, 循环卷积不难理解, 只是当充分的利用了Padding的区域, 不再将其填充为0, 而是按照循环卷积(右图)的方式对其进行循环卷积的Padding, 利用其他的位置对原来填充0的位置进行有效的填补. 为了更好地描述该过程, 写出两种卷积Padding的矩阵, 标准卷积Padding(左), 循环卷积Padding(右):
$$
\begin{array}{cc}
\begin{bmatrix}
0 & 0 & 0 \\
0 & x_{11} & x_{12} \\
0 & x_{21} & x_{22}
\end{bmatrix} &
\begin{bmatrix}
x_{44} & x_{41} & x_{42} \\
x_{14} & x_{11} & x_{12} \\
x_{24} & x_{21} & x_{22}
\end{bmatrix}
\\
\text{Standard Conv} & \text{Circular Conv}
\end{array}
$$
若写出循环卷积其数学形式, 如下:
$$
[\boldsymbol{I} \star \boldsymbol{w}]_{p, q}=\sum_{i=-\lfloor k / 2\rfloor}^{\lfloor k / 2\rfloor} \sum_{j=-\lfloor k / 2\rfloor}^{\lfloor k / 2\rfloor} \boldsymbol{I}_{[p-i]_{m},[q-j]_{n}} \boldsymbol{w}_{i, j}
$$
在做循环卷积的时候, 使用的是Depth - wise Convolution. 也就是将随机排列Reshape后的Tensor集合$\phi\left(\mathcal{P}_{t}\right)$ 在Channel维度上Stack起来, 然后对每个Channel单独进行卷积.

作者在这里还强调, 直接引入Depth维度上的卷积核参数共享能取得更好的效果.
引入循环卷积, 进一步的增加了二者的交互性.
Score Function
打分函数如下:
$$
\psi(s, r, o)=g\left(\operatorname{vec}\left(f\left(\phi\left(\mathcal{P}_{k}\right) \circledast \boldsymbol{w}\right)\right) \boldsymbol{W}\right) \boldsymbol{e}_{o}
$$
其中$\circledast$ 代表循环卷积, $\operatorname{vec}(\cdot)$ 代表Concat(其实就是Flatten), $e_{o}$ 代表尾实体的Embedding, $\boldsymbol{W}$ 代表变换矩阵. $f$ 和$g$ 分别代表$\text{ReLU}$ 和$\sigma$ 函数. 在训练时使用标准的二分类交叉熵作为损失函数, 并使用标签平滑.
Experiment
Performance Comparison
这部分的实验意在比较InteractE与现有方法的性能比较, 下面是InteractE在三个数据集上的Link Prediction效果:
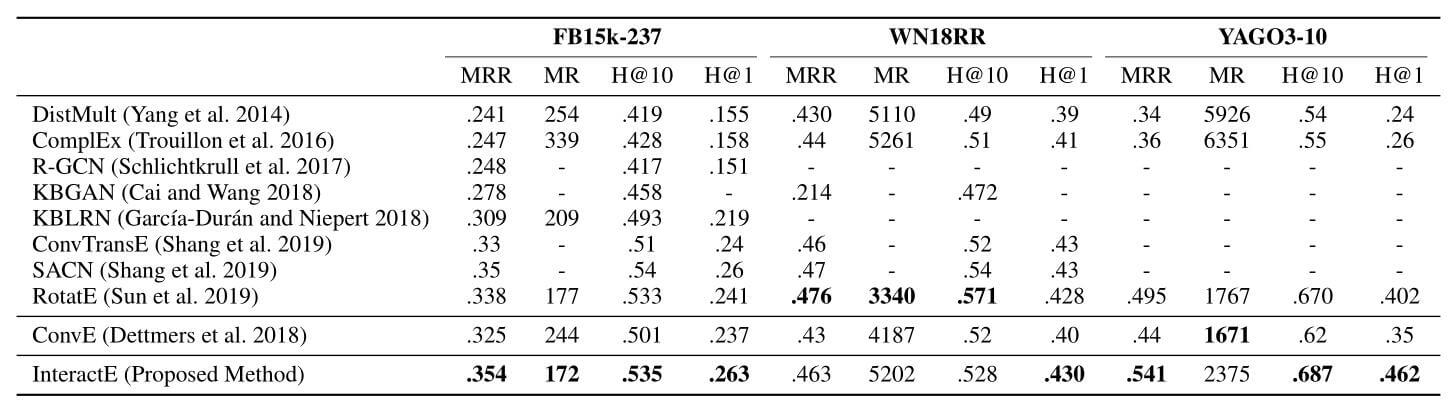
有一件非常有意思的事情, InteractE与AcrE(Serial)表现出几乎相同的性能, 而且在WN18RR上的表现也不好. 但AcrE的参数量却远少于InteractE.
我个人猜测是AcrE中使用的空洞卷积在一定程度上能与InteractE中的棋盘Reshape和循环卷积等效.
Effect of Feature Reshaping and Circular Convolution
作者列举了三种Reshape的方式, 并做了它们分别与标准卷积核循环卷积的性能对比实验:
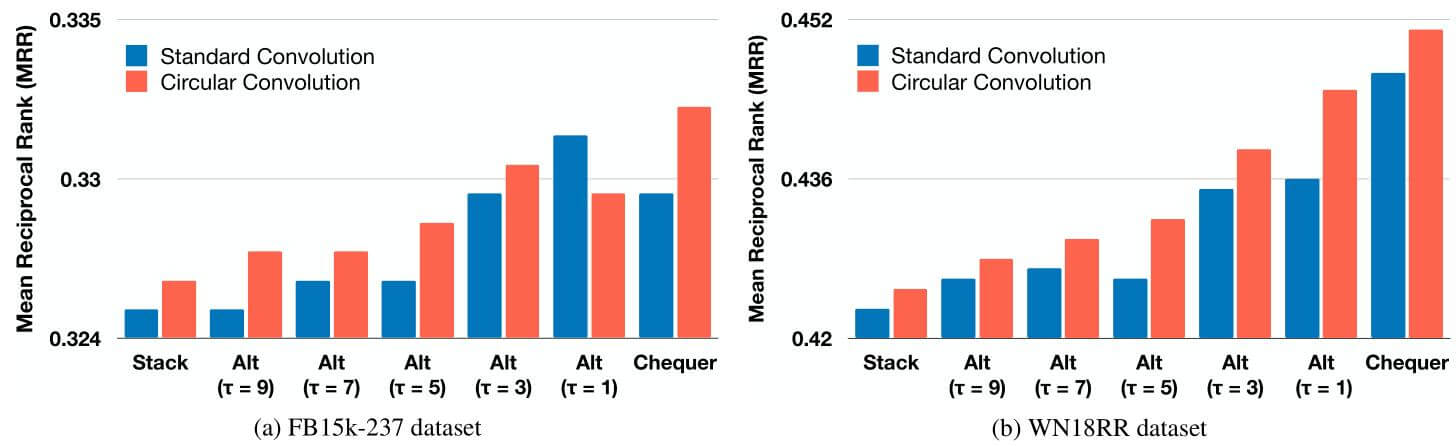
从实验结果能看出, 除了使用$\tau=1$ 的交替排列方式, 在其他所有对照组种, 循环卷积的性能均高于标准卷积. 并且, $\tau$ 被定义为是$e_s, e_r$ 间重复的交替次数, $\tau$ 越小, 异质交互次数就越多, 随着其减小, 效果明显提升.
Effect of Feature Permutations
作者选用了多种Feature Permutation, 将它们在三种不同的数据集上对比:
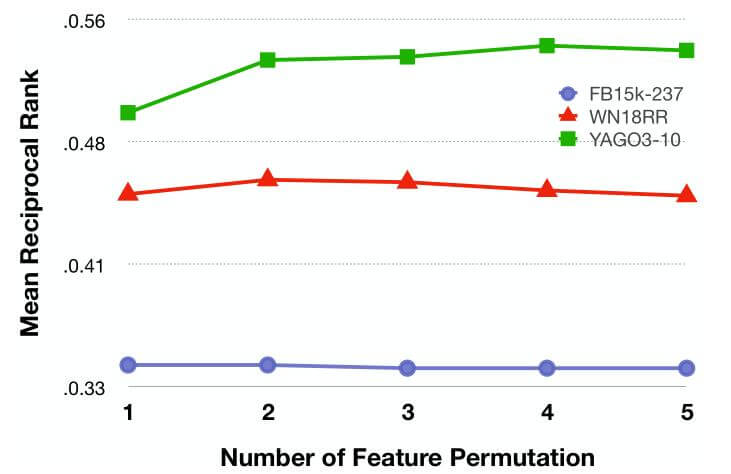
YAGO3-10的实体量要远大于FB15k-237和WN18RR. 当超过某个阈值时, 排列数量将不再影响性能, 甚至变得多余.
Evaluation on different Relation Types
作者对比了RotatE, ConvE, InteractE在不同类别上的头尾预测效果:
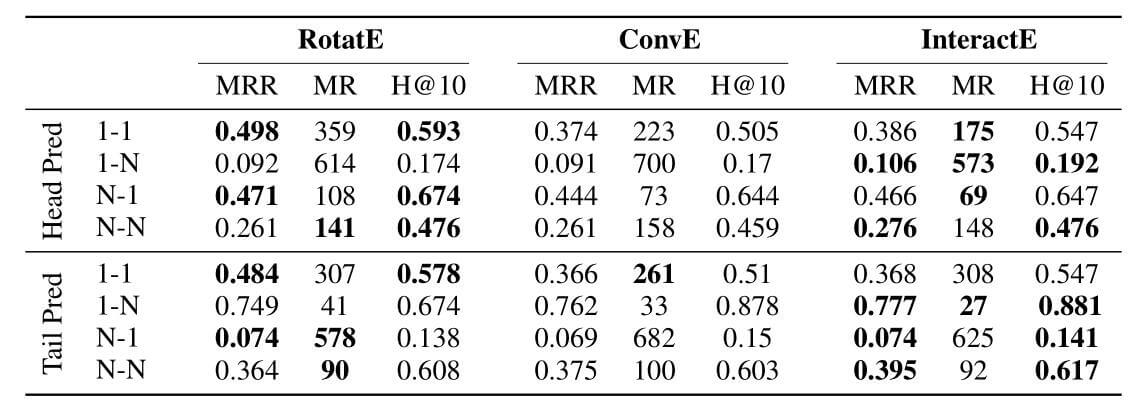
RotatE更善于处理1-1的简单一些的关系, InteractE更善于捕捉1-N, N-N的复杂关系, 佐证了交互带来的作用.
Summary
InteractE通过尽可能最大化头实体和关系Embedding的交互来获得更好的嵌入表示. 其他Embedding方法不同的是, InteractE从Permutation和Reshape两个独特的角度处理了Embedding的问题.
但不知道作者有没有考虑过其他的Encoding Model能进一步增强Embedding之间的交互, 或者是尝试使用更复杂的Reshape方式, 在卷积时扩大交互范围(相应的开销也会提高).

