本文前置知识:
- 膨胀卷积(空洞卷积)
- 残差连接
Knowledge Graph Embedding with Atrous Convolution and Residual Learning
本文是论文Knowledge Graph Embedding with Atrous Convolution and Residual Learning的阅读笔记和个人理解. 由Pytorch实现的源代码已经放到上Github, 这是NEU KG组的论文! 刚发我就看完了. 该论文已经被COLING收录. 该论文是一篇KGE方向的论文, 用极简结构实现了非常好的性能, 并在多个常用数据集上SOTA.
Basic Idea
在当今各类KGE模型大红大紫的情况下, 模型的复杂度和表达能力得不到很好的权衡. 最近流行的例如基于深度神经网络的嵌入模型, 基于图神经网络的嵌入模型, 都有非常高的耗时和模型复杂度, 导致不能在一些实时的场景下灵活运用. AcrE的目标就是实现简单, 高效的知识嵌入, 同时兼具了参数量少, 计算量低的特征.
ConvE
本节作为背景知识为AcrE铺垫, 取自Convolutional 2D Knowledge Graph Embeddings. 主要介绍KGE中的ConvE方法. ConvE只不过是将卷积使用在了KGE上, 有卷积基础的应该能够猜到使用方法, 所以不会细说.
得益于CNN的权重共享, 参数量非常少, 因此很高效, 并且很简单, 注意这个特点.
1D Convolution VS 2D Convolution
作者指出, 相较于1维卷积, 2维卷积有更强的表达能力(其实从直觉来说也是这样).
在做1维卷积时, 卷积核最多只能与左侧或右侧离得比较近的元素交互:
$$
\left(\begin{array}{lll}
\left.\left[\begin{array}{lll}
a & a & a
\end{array}\right] ;\left[\begin{array}{lll}
b & b & b
\end{array}\right]\right)=\left[\begin{array}{llllll}
a & a & a & b & b & b
\end{array}\right]
\end{array}\right.
$$
但2维卷积不一样, 除了能够与邻近的左右元素交互, 还能与上下元素进行交互:
$$
\left(\left[\begin{array}{lll}
a & a & a \\
a & a & a
\end{array}\right] ;\left[\begin{array}{lll}
b & b & b \\
b & b & b
\end{array}\right]\right)=\left[\begin{array}{lll}
a & a & a \\
a & a & a \\
b & b & b \\
b & b & b
\end{array}\right]
$$
如果两种元素代表的意义不同, 那么交换它们的拼接方式还能进一步的提升交互次数:
$$
\left[\begin{array}{lll}
a & a & a \\
b & b & b \\
a & a & a \\
b & b & b
\end{array}\right]
$$
由于交换了Concat方式, a和b交错, 能够实现更多次交互.
ConvE Architecture
直接看图:
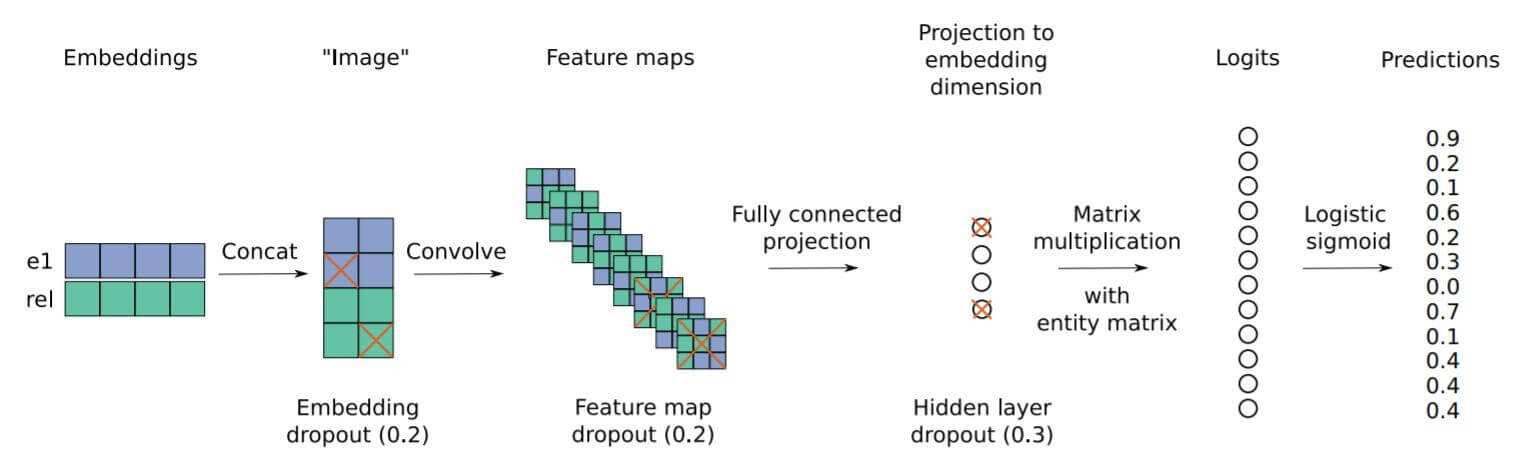
整体流程也是非常简单, 将头实体和关系先Embedding, 然后再Reshape到一个合适的尺寸, 然后就用卷积来提取特征, 用全连接将其投影到与Embedding大小相同的隐空间中, 最后将隐空间的映射和尾实体的Embedding做相似度比较.
按照描述, 打分函数为:
$$
\psi_{r}\left(\mathbf{e}_{s}, \mathbf{e}_{o}\right)=f\left(\operatorname{vec}\left(f\left(\left[\overline{\mathbf{e}_{s}} ; \overline{\mathbf{r}_{r}}\right] \ast \omega\right)\right) \mathbf{W}\right) \mathbf{e}_{o}
$$
其中$\mathbf{e}_{s}, \mathbf{e}_{o}$ 分别代表头实体和尾实体的Embedding, $\overline{\mathbf{e}_{s}}, \overline{\mathbf{r}_{r}}$ 分别代表Reshape后的头实体和关系向量. $\omega$代表卷积核, $\mathbf{W}$ 代表投影矩阵. 这种方式通过内积来比较所获向量与尾实体的相似度, 越相似得分越高.
然后将该得分经过$\sigma$ 函数, 得到每个实体的概率:
$$
p=\sigma(\psi_{r}\left(\mathbf{e}_{s}, \mathbf{e}_{o}\right))
$$
使用二分类交叉熵进行优化:
$$
\mathcal{L}(p, t)=-\frac{1}{N} \sum_{i}\left(t_{i} \cdot \log \left(p_{i}\right)+\left(1-t_{i}\right) \cdot \log \left(1-p_{i}\right)\right)
$$
$t$ 是尾实体的独热编码向量. 除此外还加入了Dropout, BatchNorm, 标签平滑等防止过拟合的手段.
AcrE
AcrE(Atrous Convolution and Residual Embedding), 在ConvE的基础上主要做了两点改动, 也就是我们开头所需的前置知识, 空洞卷积和残差连接.
Atrous Convolution
Atrous Convolution也称空洞卷积或膨胀卷积. 由于空洞卷积只是作为一种CNN的变体形式的卷积, 因此它的机制在此不做过多讨论.
空洞卷积相较于普通卷积, 有了一个新的参数”膨胀率“. 它指的是在卷积下, 每个卷积核元素之间的距离 - 1. 空洞卷积能在不引入额外参数的情况下获得更大的感受野, 如下图:
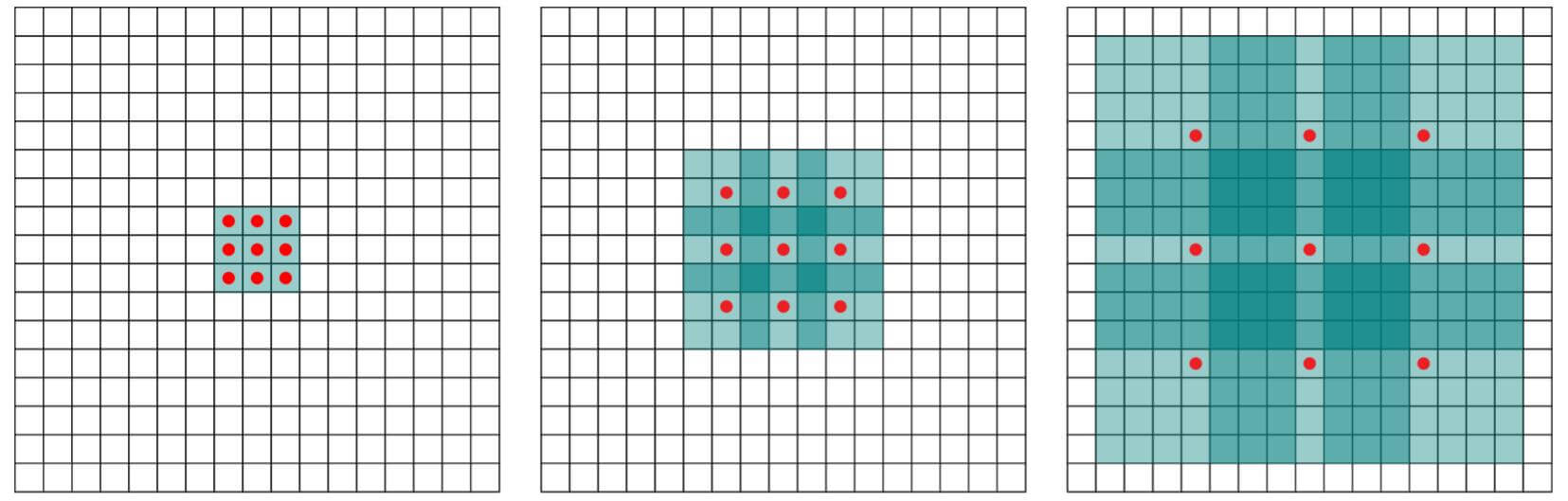
上图取自Multi-Scale Context Aggregation by Dilated Convolutions.
| 最左侧 | 正中间 | 最右侧 | |
|---|---|---|---|
| 卷积核 | (3, 3) | (3, 3) | (3, 3) |
| 感受野 | $3 \times 3$ | $7 \times 7$ | $15 \times 15$ |
| 膨胀率 | 1 | 2 | 4 |
空洞卷积常在语义分割和图像重建上使用, 与之相对的, 使用空洞卷积也会带来一些弊端, 如有需求请自行查询相关内容.
在AcrE中, 它用来解决CNN在连续重复的下采样和池化而导致特征图分辨率丢失问题. 个人认为, 由于空洞卷积扩大了感受野, 能进一步增加实体和关系Embedding之间的交互, 以此将头实体和关系更紧密的联系到一起.
Residual Connection
引入残差连接主要的原因有两个:
- 梯度爆炸和梯度消失.
- 多次卷积导致的原始信息丢失问题.
在ConvE中, 作者没有使用残差连接. 关于残差连接, 不懂可以去我之前写的<卷积神经网络发展史>中了解.
AcrE Architecture
AcrE有两种结构, 分别是串行(Serial)结构和并行(Parallel)结构. 无论哪种都使用了空洞卷积和残差连接. 但无论哪种结构都必须要有标准卷积的作用, 膨胀卷积虽然会提供更大的感受野, 但也有可能会因膨胀丧失局部信息.
2D Embedding Representation
在ConvE中已经提到, 1D卷积没有2D卷积的表达能力强, 而且2D卷积能更多的增强头实体和关系间的交互, 所以都使用的是2D卷积. AcrE中, 首先要说一下KG中的三元组在2D中的表示方法, 可以视作是预处理. 对于三元组$<h, r, t>$, $\mathbf{h}, \mathbf{r}, \mathbf{t}$分别代表头实体, 关系和尾实体.
若$\tau$ 代表Reshape操作, $\mathbf{e}$ 代表实体的Embedding, $\mathbf{r}$ 代表关系的Embedding, $[;]$ 代表Concat, 则2D中的嵌入表示方法是$\tau([\mathbf{e};\mathbf{r}])$.
Serial AcrE Model
在串行AcrE中, Embedding由一系列串行的卷积动作和最后的Flatten.

Standard Convolution based Learning
在串行AcrE中, 将Reshape后的Embedding先经过标准卷积, 得到结果$\mathbf{C}_{0}$:
$$
\mathbf{C}_{0}^{i}=\omega_{0}^{i} \star \tau([\mathbf{e} ; \mathbf{r}])+\mathbf{b}_{0}^{i}
$$
其中$\star$ 代表卷及操作, $\omega_{0}^{i}$ 代表第i个卷积核, $b_0^i$ 代表第i个偏置. 假设有$F$ 个卷积核, 则$\mathbf{C}_{0}=\left[\mathbf{C}_{0}^{1}: \mathbf{C}_{0}^{2}: \mathbf{C}_{0}^{3}: \ldots: \mathbf{C}_{0}^{F}\right]$, 之后该卷积结果会经过一系列的空洞卷积.
关于池化, 这里必须要提一下.
在CV任务中是卷积和池化交替使用, 因为其信息量通常是冗余的, 池化能够减小特征图的尺寸, 相当于求平均或最大值的效果, 池化有利于后面卷积抽取更关键的特征.
但目前在NLP相关的任务中, 信息非常复杂, 使用池化直接就导致了信息的损失. 并且, 因为我们是想将头实体和尾实体还有关系Embedding进一个同维度的空间下的, 如果使用池化会导致维度变化.
最后指出, 在实验中加入池化并没有很大程度的影响性能.
Atrous Convolution based Learning
“空洞卷积大致是什么”这个问题在前面已经解决了, 其实就是在卷积核各元素之间插入一些小洞. 对于给定的输入向量$\mathbf{x}$, 长度为$K$的卷积核向量$\mathbf{w}$, 在空洞卷积下的输出$\mathbf{y}$ 由如下方式得来:
$$
y_{i}=\sum_{k=1}^{K} x_{i+l \times k} \times w_{k}
$$
其中$l$ 是膨胀率, 标准卷积的膨胀率为1.
在串行AcrE中, 卷积是一个接着一个串行的:
$$
\mathbf{C}_{\mathbf{t}}=\omega_{\mathbf{t}} \star \mathbf{C}_{t-1}+\mathbf{b}_{\mathbf{t}}
$$
$\mathbf{C}_{t-1}$ 代表上个卷积的输出结果, $\omega_{\mathbf{t}}$ 和$\mathbf{b}_{\mathbf{t}}$ 分别是卷积核和偏置向量.
Feature Vector Generation
在串行的AcrE中, 不同种卷积一个接一个的执行, 每个卷积都能从之前抽取不同的实体和关系交互. 但越多的卷积使用, 就会导致越多的原始信息丢失, 这就导致了模型在学习时忘记了抽取出的特征到底有没有用. 同时, 为了缓解梯度爆炸和梯度消失, 在这使用残差连接来弥补原来丢失的信息. 在残差连接后, 紧接着使用ReLU做激活函数, 并做Flatten:
$$
\mathbf{o}=\text {Flatten}\left(\operatorname{ReLU}\left(\mathbf{C}_{T}+\tau([\mathbf{e} ; \mathbf{r}])\right)\right)
$$
其中$\mathbf{C}_{T}$ 是最后一个空洞卷积的输出, $T$ 是空洞卷积的次数.
Parallel AcrE Model
并行AcrE分别执行卷积后聚合.
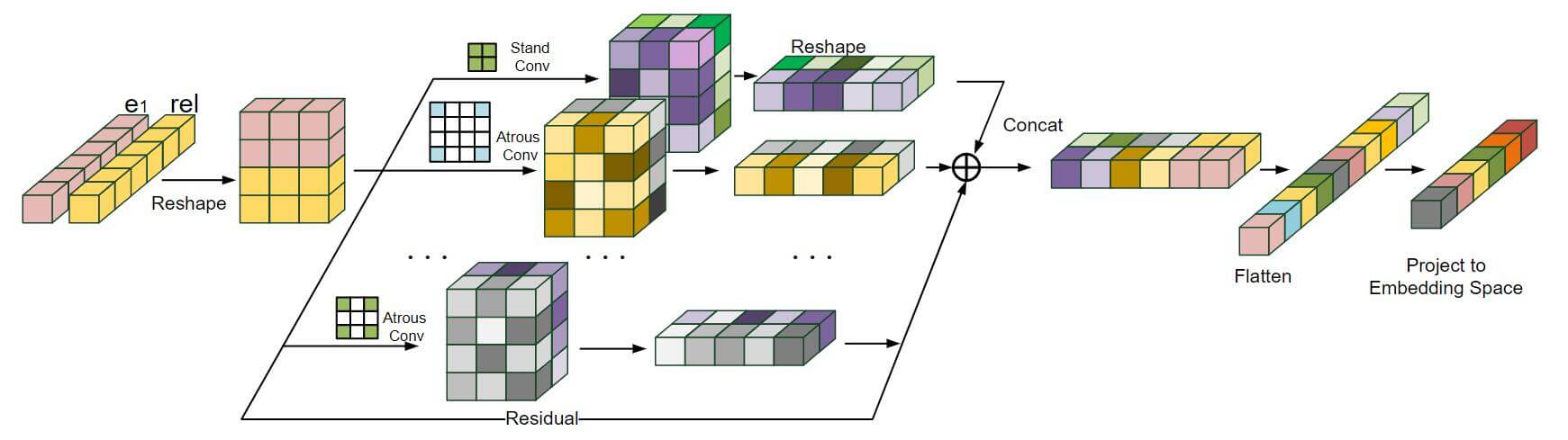
注意, 在并行结构图中所示的卷积类型是不同的! 使用不同膨胀率的卷积核.
Results Integration
与串行形态的AcrE不一样, 并行形态下, 2D Embedding分别用不同形式的卷积计算, 最后以某种形式聚合到一起.
$$
\mathbf{C}=\mathbf{C}_{\mathbf{0}} \oplus \mathbf{C}_{\mathbf{1}} \oplus \ldots \oplus \mathbf{C}_{\mathbf{T}}
$$
其中$\mathbf{C}_{\mathbf{0}}$ 是标准卷积, $\mathbf{C}_{\mathbf{i}}$ 是第i个空洞卷积. $\oplus$ 意味着某种聚合操作, 可以是基于Concat的操作, 也可以是基于加的操作等等. 在实验中会比较这两种方式的性能差异.
Feature Vector Generation
与串行AcrE相仿, 将每个卷积结果聚合, 再加上残差的信息, 然后用ReLU, 再经过一次变换, 最后Flatten.
$$
\mathbf{c}=\text {Flatten}\left(\mathbf{W}_{\mathbf{1}} \operatorname{ReLU}(\mathbf{C}+\tau([\mathbf{e} ; \mathbf{r}]))\right)
$$
其中$\mathbf{W_1}$ 是变化矩阵, 这是比串行结构多出来的地方.
我个人认为并行结构下的AcrE与Inception(详见卷积神经网络发展史)中的多尺度是相同的道理, 通过不同的膨胀率实现了对实体和关系向量多个角度的抽取, 最后Concat到一起, 每个不同感受野的膨胀卷积都能提供不同的信息.
Score Function and Loss Function
Score Function
打分函数其实与ConvE相似, 将输出向量先经过变换矩阵加上偏置, 再用点积比较与尾实体的相似度:
$$
\psi(h, r, t)=(\mathbf{o} \mathbf{W}+\mathbf{b}) \mathbf{t}^{\top}
$$
其中$\mathbf{W}, \mathbf{b}$ 分别是变化矩阵和偏置向量. 接着用$\sigma$ 函数获得所有候选实体的概率:
$$
p(t \mid h, r)=\operatorname{sigmoid}(\psi(h, r, t))
$$
Loss Function
这点和ConvE一样, 使用了交叉熵作为损失函数:
$$
\mathcal{L}=-\frac{1}{N} \sum_{i=1}^{N}\left[t_{i} \log p\left(t_{i} \mid h, r\right)+\left(1-t_{i}\right) \log \left(1-p\left(t_{i} \mid h, r\right)\right)\right]
$$
其中$\mathbf{t}$ 是尾实体的独热编码.
Other Details
和ConvE一样, BatchNorm和卷积的向性比较好, 所以也使用了BatchNorm. 包括标签平滑啊之类的trick也都从ConvE沿用了下来.
Experiment
在实验的代码中, 只使用了三个卷积核. 有一个标准卷积核和两个不同膨胀率的膨胀卷积核.
Settings
DataSets
我们将其他KGE方法在如下六个常用数据集中对比:
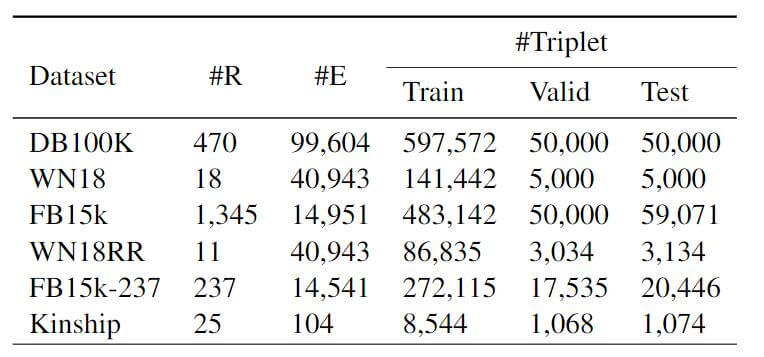
Evaluation
实验部分均采用Link Prediction的任务将其他KGE方法与AcrE进行对比. Link Prediction是基于已知的某端实体和关系对未知的另一端实体进行预测的任务. 即对于三元组$<h,r,t>$, 已知$<h,r>$ 预测$t$, 或已知$<t,r>$ 预测$h$. 并使用Hit@k, MRR作为指标进行对比.
Results
Benchmark Datasets Experiment
在DB100k中的实验结果, 上面的内容全部取自SEEK的论文SEEK: Segmented Embedding of Knowledge Graphs:

还有在其他五个数据集上的表现:
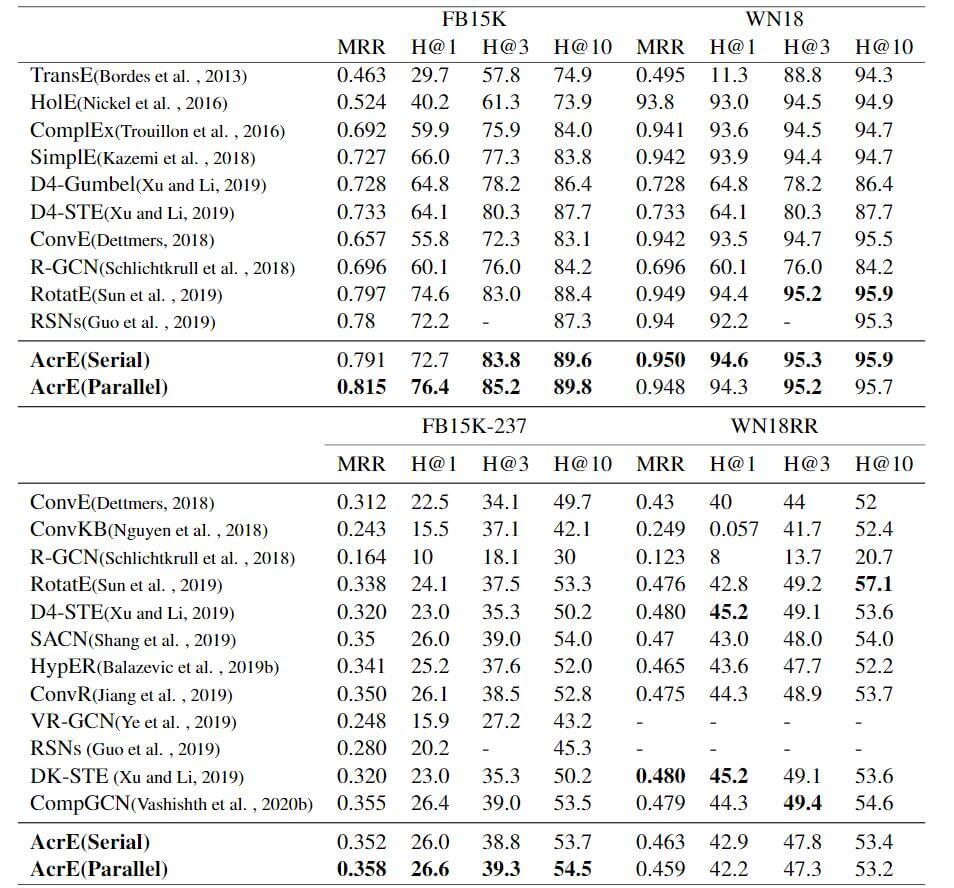
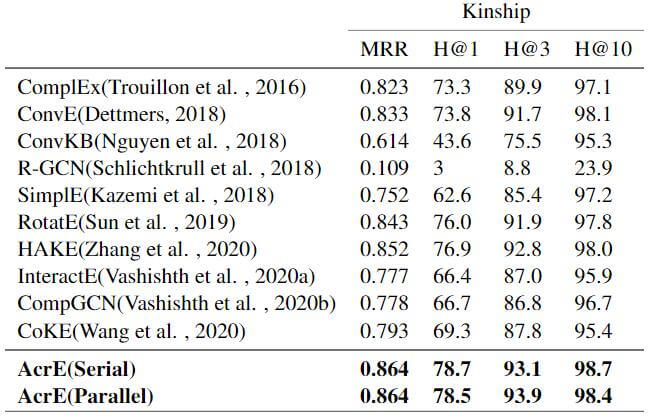
只是在WN18RR上没有取得太好的效果, 在其他数据集上均SOTA或在平均性能上超过其他KGE方法.
实验的细节分了区分头尾的预测和按类别预测两种.
下面是区分头尾的预测:

直接SOTA.
下面是按类别预测:
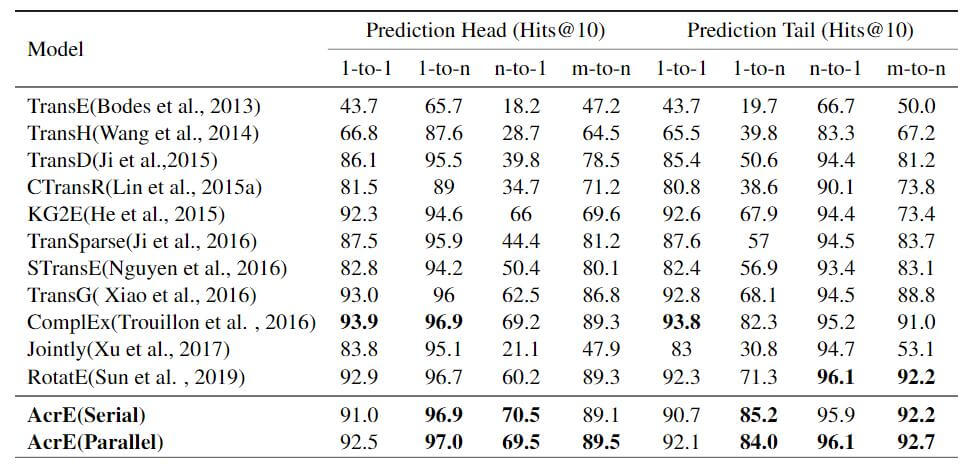
Ablation Experiment

消融实验主要进行了如下工作:
- 将串行和并行的AcrE对比, 发现一般情况下串行的AcrE都比并行AcrE性能要差.
- 将带有残差连接的AcrE和去掉残差连接的AcrE对比, 发现去掉后性能有明显下降, 说明了残差连接对AcrE非常重要.
- 将并行用Concat方式聚合的AcrE和并行用Add方式聚合的AcrE对比, 发现Concat效果要好一些.
Parameters Comparison
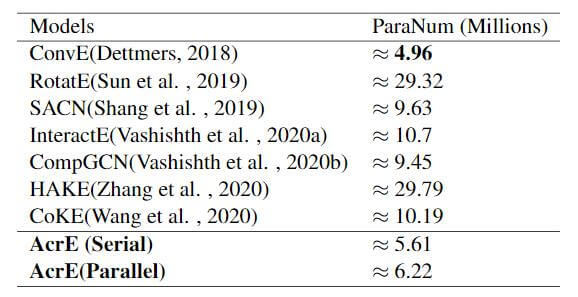
ConvE的参数虽然比AcrE要少, 但在前面的对比实验中知道效果并没有AcrE好. AcrE的参数量要远少于除了ConvE的所有模型. 并且并行结构比串行结构的模型要稍大一些, 因为最后多一次变换.
另外, 调参的部分碍于篇幅问题, 没有在论文中贴出. 能够选择的参数范围非常小, 还是比较好调的, 参数在源码中都可以找到.
关于计算效率的优势, 因为涉及到其他训练的参数影响, 没法提供一个非常公平的环境去验证. 但作为ConvE的变体, 运行时间的复杂度应该与ConvE相仿.
Summary
该论文简单易懂, 只看嵌入方式的图示和表格中给出的实验结果就能够把握文章重点. 尤其是最后的消融实验体现出了残差连接起到的作用. AcrE本身结构就简单到了令人发指的地步, 非常不可思议它甚至能达到一些高复杂度模型的结果…
在实验部分将那些没有在指定数据集上给出实验结果的论文的Embedding方法全都跑了一遍, 并做了大量的对比实验证明AcrE的有效性. 并且这是第一次将不同形式的卷积用到了KGE上的研究工作.

