发布日期: 2023-02-10

更新日期: 2025-03-23

文章字数: 3.3k

阅读时长: 13 分

Query-based Instance Discrimination Network for Relational Triple Extraction

本文是论文Query-based Instance Discrimination Network for Relational Triple Extraction 的阅读笔记和个人理解, 论文来自EMNLP 2022.

Basic Idea

作者认为, 现有的方法在抽取三元组时要么是通过立体透视图的方法, 要么是学到每一种关系的独立分类器来完成Tagging:

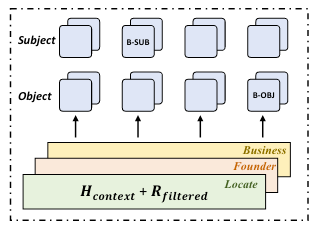
几乎之前的所有方法都可以归类到这类中, 这大类方法仍然导致有误差错误传播, 关系冗余, 以及缺少三元组之间的高级连接的问题.

作者提出了一种对三元组Instance Level的表示方法, 通过Query Embedding对Token Embedding完成一步抽取, 从而规避上述问题:

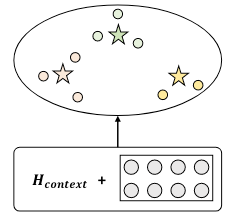
图示中的星星代表Relation Type Embedding, 而圆圈代表Query Embedding, 不难看出作者的应该要尽可能让同关系下的Query Embedding环绕在Relation Embedding周围. 这种方法在空间中可以保留关系之间的语义信息, 对比学习可以达到这种目的.
另外, 看到Query Embedding这个词的时候, 对CV略有了解的小伙伴可能会想到近年在CV中影响力很大的DETR: End-to-End Object Detection with Transformers, 事实上本文也是DETR在NLP中的应用. 如果对DETR还不了解, 建议花几分钟时间阅读一下DETR的架构(其实就是标准的Transformer)和基本思想, 非常简洁也非常简单. 如果你只知道SPN而不知道DETR, 也可以不看DETR, 因为SPN和DETR几乎完全一致.

QIDN

QIDN的概览模型图如下:

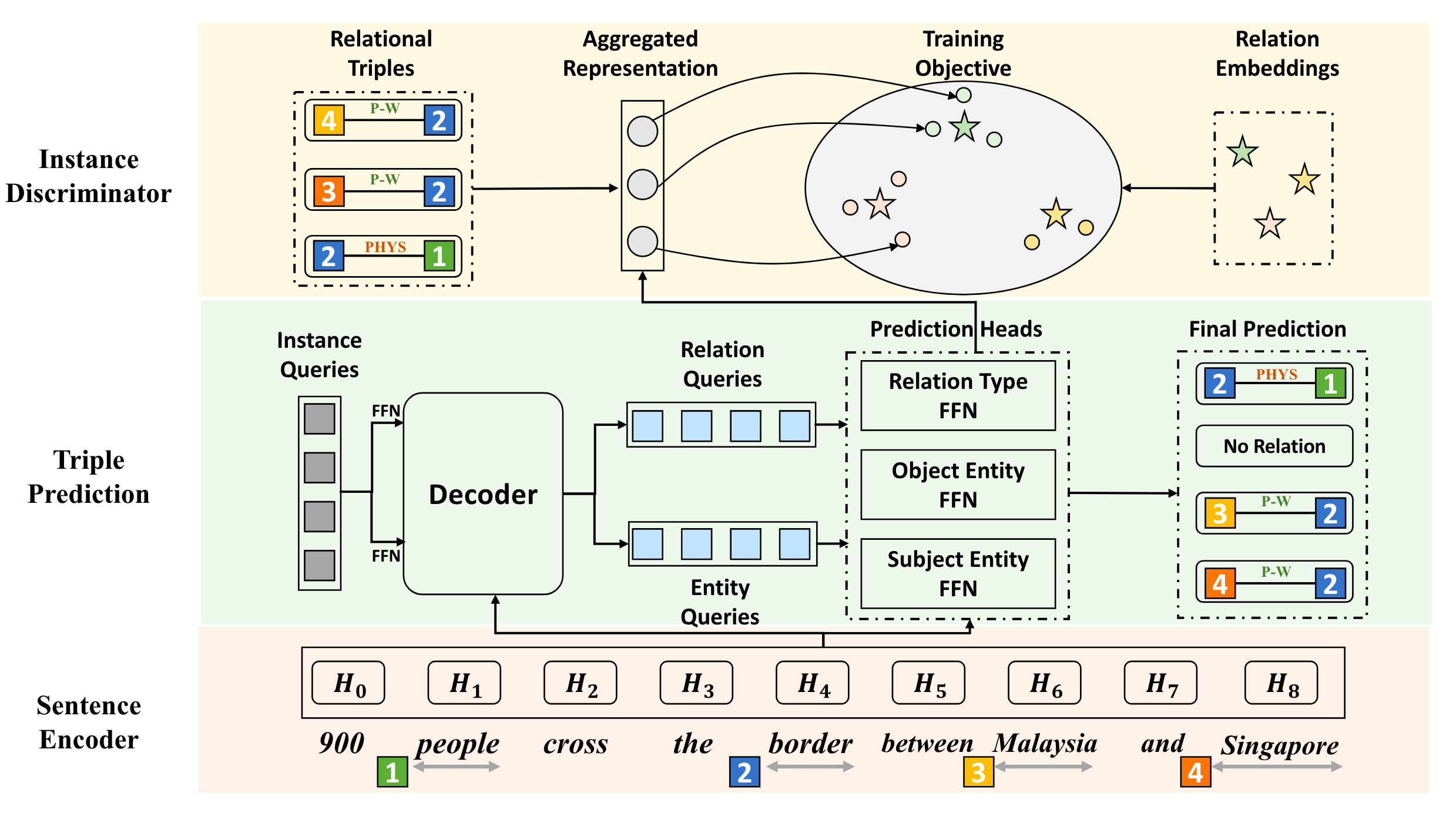
在经过Sentence Encoder编码后, 结合Query在Decoder中完成Triple Prediction. 此外, 使用Instance Discriminator在空间中用对比学习约束预测头得到的三元组表示.

Task Formulation

对于输入句子$X=x_1, x_2, \ldots, x_n$, 实体集$\mathcal{E}$ 中的实体可以被表示为$(x_i, x_j, t_e)$, $x_i, x_j$ 分别为实体的左右边界Token. 而$t_e$ 代表预定义好的实体类型集合$\mathcal{Y}_e$ 中的实体类型.

对于关系集合$\mathcal{R}$, 每种关系被表示为$(e_1, e_2, t_r)$, $e_1, e_2 \in \mathcal{E}$ 分别为头实体和尾实体, $t_r$ 为预定义好的关系集合$\mathcal{Y}_r$ 中的关系类型. 除此外, 在$\mathcal{Y}_e, \mathcal{Y}_r$ 中还有$\varnothing$ 代表没有识别到任何关系或者任何实体.

Sentence Encoder

对于输入句子$X$, 作者用BERT获取它每个Token的上下文表示, 然后送入一个双层LSTM获得最终的句子表示$H \in \mathbb{R}^{n\times d}$, 其中$n, d$ 分别为句子长度和Hidden size.

Triple Prediction

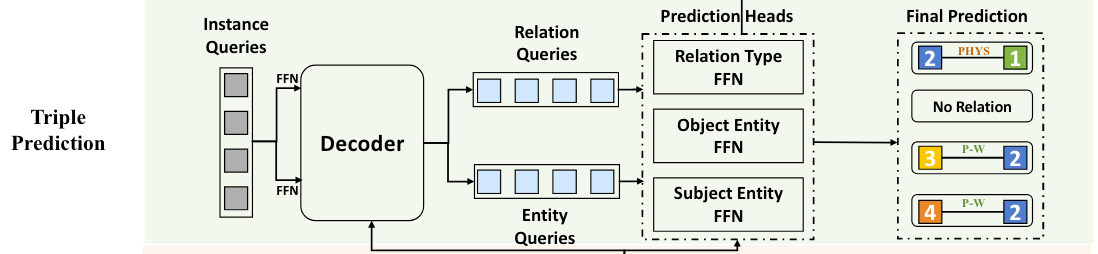
作者使用$M$ 个Instance Level Query $Q=\mathbb{R}^{M\times d}$来查询句子中所包含的所有三元组.

DETR最早被用于目标检测, 每个Query都对应了图像中的一个目标(Bounding Box和物体类别). 与之类似的, 在QIDN中, 每个Query对应着一个关系三元组.

由于RTE任务需要抽取出关系特定下的头尾实体, 这意味着每个Query Embedding不但能指出对应的头尾实体, 还有头尾实体间关系, 所以在这个模块中作者需要构建对实体和关系的两种Query.

Transformer - based Decoder

Decoder是由$L$ 层的Transformer Decoder的堆叠, 其中Attention计算方式如下:

$$
\text { Attention }(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) V
$$

其中$Q, K, V$ 分别为Query, Key, Value矩阵, $1/\sqrt{d_k}$ 为缩放因子.

Transformer Decoder的堆叠可以记为:

$$
\operatorname{Decoder}(Q, H^\prime) = \operatorname{Attention}(Q, H^\prime, H^\prime)
$$

在DETR的架构中, Decoder端的Query便是Query Embedding, Key和Value则是原图信息.

在QIDN中, 作者没有直接使用Sentence Encoder中的$H$ 作为Decoder中需要的Key和Value, 而是构造了一种Span Level的表示来获得层次语义信息. 令$S=s_1, s_2, \ldots, s_{n_s}$ 为句子$X$ 中所有的Span, 对于任意一Span $s_i \in S$, 其Span表示$H_i^{span}$ 为$H$ 中的Span边界表示和长度Embedding的拼接:

$$
H_{\mathrm{i}}^{\text {span }}=\left[H_{\text {start }(\mathrm{i})} ; H_{\mathrm{end}(\mathrm{i})} ; \phi\left(s_{\mathrm{i}}\right)\right]
$$

$[;]$ 为拼接操作, $H_{\text {start }(\mathrm{i})} , H_{\mathrm{end}(\mathrm{i})}$ 分别为起始和结束Token的表示, $\phi(s_i)$ 为NER中Span based方法常用的长度Embedding, 可以加入一些Span的长度信息. 最终Span Level的表示为$H^{span} \in \mathbb{R}^{n_s \times d}$.

我认为在这里选择Span作为单位构建表示, 可以获得大量的负样本, 有利于对比学习.

前面提到过, 同一个Query需要同时能够抽取关系和实体, 因此作者将每个Query兵分两路, 变为Relation Query $Q_r$和Entity Query $Q_e$:

$$
\left[Q_r ; Q_e\right]=\operatorname{Decoder}\left(\left[Q W_r ; Q W_e\right], H^{\text {span }}\right)
$$

其中$W_r, W_e \in \mathbb{R}^{d \times d}$ 为可训练参数.

更直观一点的话, 作者将Decoder的结构放在附录里:

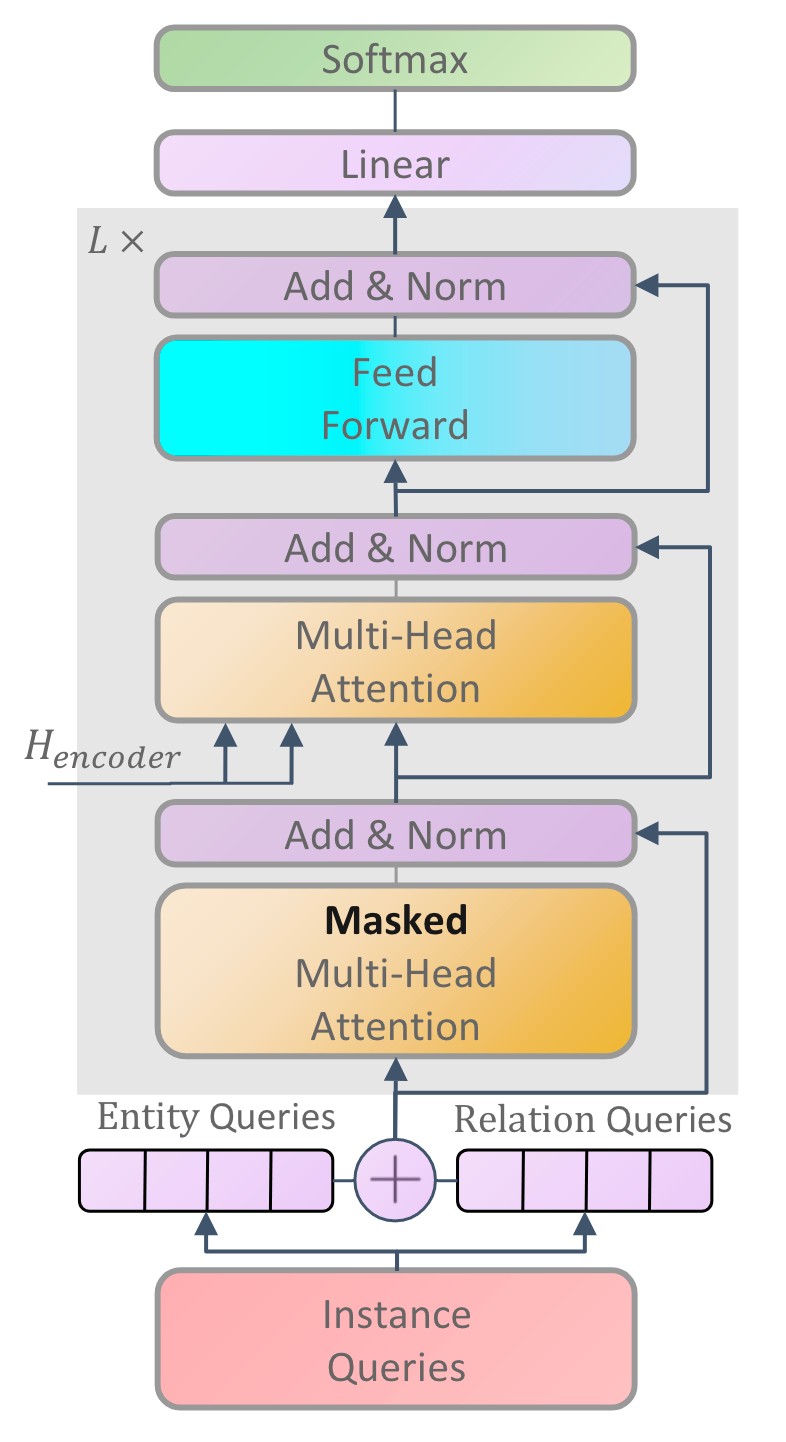
其实就是普通Transformer Decoder, 主要区别在于Query的生成拆分为了Entity Query和Relation Query两个branch, 并且在Cross Attention中采用的Key和Value是Span Level的.

综上, 如果有了成对的$Q_r, Q_e$, 就可以用简单的预测头将每个$Q$ 所对应的三元组预测出来.

Relation Head

对于Relation Query $Q_r$, 将其送入一个FFN中来预测第$i$ 个Query $Q_r^i$ 对应三元组的关系类型$c$ 的概率$P_{i c}^t$:

$$
P_{i c}^t=\frac{\exp \left(Q_r^i W_t^c+b_t^c\right)}{\sum_{c^{\prime}}^{\left|\mathcal{Y}_r\right|} \exp \left(Q_r^i W_t^{c^{\prime}}+b_t^{c^{\prime}}\right)}
$$

其中$W_t \in \mathbb{R}^{|\mathcal{Y}_r| \times d}, b_t \in \mathbb{R}^{|\mathcal{Y}_r|}$ 为可学习参数.

Entity Head

为了预测三元组中实体的边界, 作者将Entity Query $Q_e$ 和Token表示$H$ 都经过FFN变换:

$$
\begin{aligned}
E_\delta=Q_e
W_{\delta}\\
H_s=H W_s
\end{aligned}
$$

其中$\delta \in \mathcal{C} =\set{l_{sub}, r_{sub}, l_{obj}, r_{obj}}$ 代表Subject或者Object的左右边界, $W_\delta, W_s \in \mathbb{R}^{d \times d}$ 为可训练参数.

接着用余弦相似度$S(\cdot)$ 来衡量Entity Query生成的新表示$E_\delta$ 和原文表示$H_s$ 之间的相似度得分:

$$
S\left(\mathbf{v}_i, \mathbf{v}_j\right)=\frac{\mathbf{v}_i}{\left\Vert\mathbf{v}_i\right\Vert} \cdot \frac{\mathbf{v}_j}{\left\Vert\mathbf{v}_j\right\Vert}
$$

根据得分, 做个Softmax就可以得到第$i$ 个Entity Query对应的边界Token是第$j$ 个Token的概率:

$$
P_{i j}^\delta=\frac{\exp S\left(E_\delta^i, H_s^j\right)}{\sum_{j^{\prime}}^n \exp S\left(E_\delta^i, H_s^{j^{\prime}}\right)}
$$

其中$n$ 为句子中Token的数量.

通过Relation Head, 可以得到Instance Query $Q$ 对应的三元组关系类型$c$, 通过Entity Head, 就可以用相似度得到三元组中Subject和Object的左右边界, 由此来确定Query对应的三元组.

Instance Discriminator

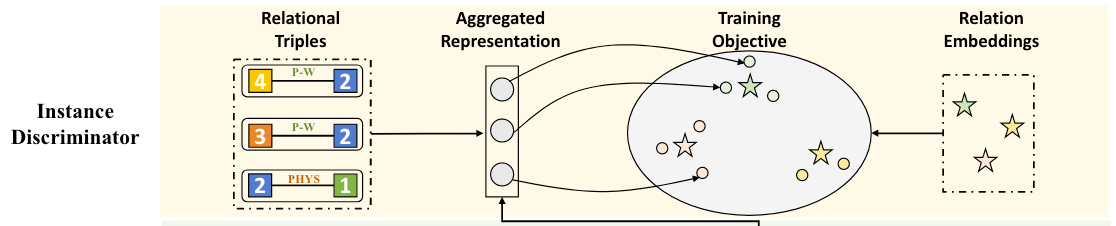
在Instance Discriminator中, 作者希望把预测头中得到的表示进一步聚合, 当做最初的三元组表示, 并在空间中使这些三元组表示满足某种约束, 来建立三元组之间的全局链接, 并且让它们具有类别语义信息.

Aggregation

首先要用关系头的表示$Q_r$, 然后简单的把它们相加到一起, 聚合成三元组初始表示$\mathbf{v}$:

$$
\mathbf{v}=Q_r W+\sum_{\delta \in \mathcal{C}} E_\delta
$$

这里对$Q_r$ 做一次变换是为了和Entity Head对齐, 因为$E_\delta$ 已经是由$Q_e$ 做了一次变换得到的.

Training Objective

对于关系集$\mathcal{R} = \set{\mathbf{r}_1, \cdots, \mathbf{r}_{|\mathcal{Y}_r|}}$, 对每种关系都建立一个随机初始化的Relation Type Embedding, 作为关系的表示.

作者希望三元组实例和关系嵌入在空间中满足下述两个特点:

对于三元组实例和实例之间, 应满足同关系内更近, 不同关系的更远.
对于三元组实例和关系之间, 应满足三元组和自身关系对应的关系嵌入更近.

对比学习就是做这个的, 所以作者使用InfoNCE来建模上述两个要求.

对于第一个特点, 同关系三元组更近, 不同关系三元组更远:

$$
\mathcal{L}_{\mathrm{ins}}=-\sum_c \sum_{i, j} \log \frac{\exp S\left(\mathbf{v}_i^c, \mathbf{v}_j^c\right)}{\sum_{c^{\prime}, j^{\prime}} \exp S\left(\mathbf{v}_i^c, \mathbf{v}_{j^{\prime}}^{c \prime}\right)}
$$

其中$(\mathbf{v}_i^c, \mathbf{v}_j^c)$ 代表同种关系类型$c$ 下的实例对.

与之类似的, 第二个特点要求三元组和自身对应的关系更近:

$$
\mathcal{L}_{\mathrm{cls}}=-\sum_{i, c} \log \frac{\exp S\left(\mathbf{v}_i^c, \mathbf{r}_c\right)}{\sum_{c^{\prime}} \exp S\left(\mathbf{v}_i^c, \mathbf{r}_{c^{\prime}}\right)}
$$

其中, $\mathbf{v}_i^c$ 是关系$c$ 的三元组实例, $\mathbf{r}_c \in \mathcal{R}$ 是关系$c$ 对应的关系嵌入.

这样就建模了关系之间的语义信息, 而不是让不同关系独立学习, 并且使得不同关系的三元组之间存在全局链接.

Training and Inference

Training

在训练时, 记三元组预测Loss $\mathcal{L}_{tri}$ 为每个Instance Query自身所对应的最优匹配三元组的关系类型预测交叉熵和头尾实体左右边界的交叉熵之和:

$$
\mathcal{L}_{\text {tri }}=-\sum_{i=1}^M\left(\log P_{\sigma(i)}^t+\sum_{\delta \in \mathcal{C}} \log P_{\sigma(i)}^\delta\right)
$$

$M$ 为Query的数量, $\sigma$ 为最优匹配的三元组.

如果还不清楚”最优匹配”, 可以看DETR中的Loss部分, 也可以看SPN的二部图匹配Loss部分.

最终的Loss为前面提到的对比学习Loss和三元组预测Loss之和:

$$
\mathcal{L} = \mathcal{L}_{tri} + \mathcal{L}_{ins} + \mathcal{L}_{cls}
$$

Inference

在推理时:

三元组可以由Instance Query$\mathcal{Y}_i=\left(\mathcal{Y}_i^t, \mathcal{Y}_i^\delta\right), \delta \in \mathcal{C}$ 得到.
关系类型预测可以由$\mathcal{Y}_i^t=\arg \max _c\left(P_{i c}^t\right)$ 得到.
头尾实体的左右边界可以由$\mathcal{Y}_i^\delta=\arg \max _k\left(P_{i k}^\delta\right)$ 得到.
预测类型为$\varnothing$ 的三元组直接被滤去.

Experiments

详细的参数设置请参照原论文.

Dataset

作者选用了RTE中常用的三个数据集NYT, WebNLG*, NYT*, 和ERE中常用的数据集ACE05和SciERC, 统计信息如下:

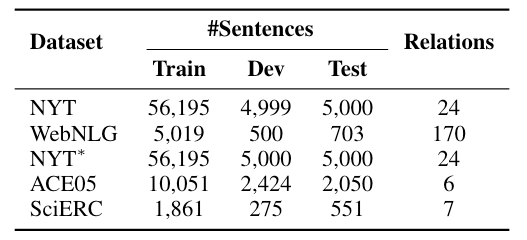
在作者的论文中, 部分匹配数据集为是不带*的, 而精准匹配是带*的. 和RTE论文的习惯刚好相反. 也就是说, 作者写的是WebNLG, 后续实验结果实际上是WebNLG*, NYT和NYT*也要颠倒一下, 下同.

Overall Performance

QIDN在RTE三个数据集NYT, WebNLG*, NYT* 上结果如下:

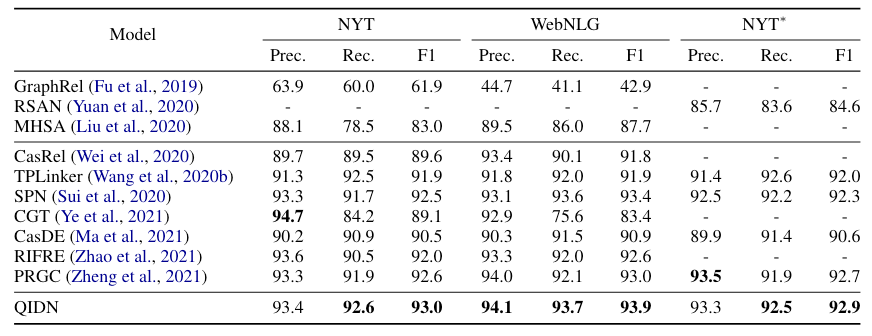
QIDN相较于作者给出的Baseline有非常大的进步, 这个性能其实也挺能打的.

在ERE上两个数据集ACE05和SciERC上结果如下:

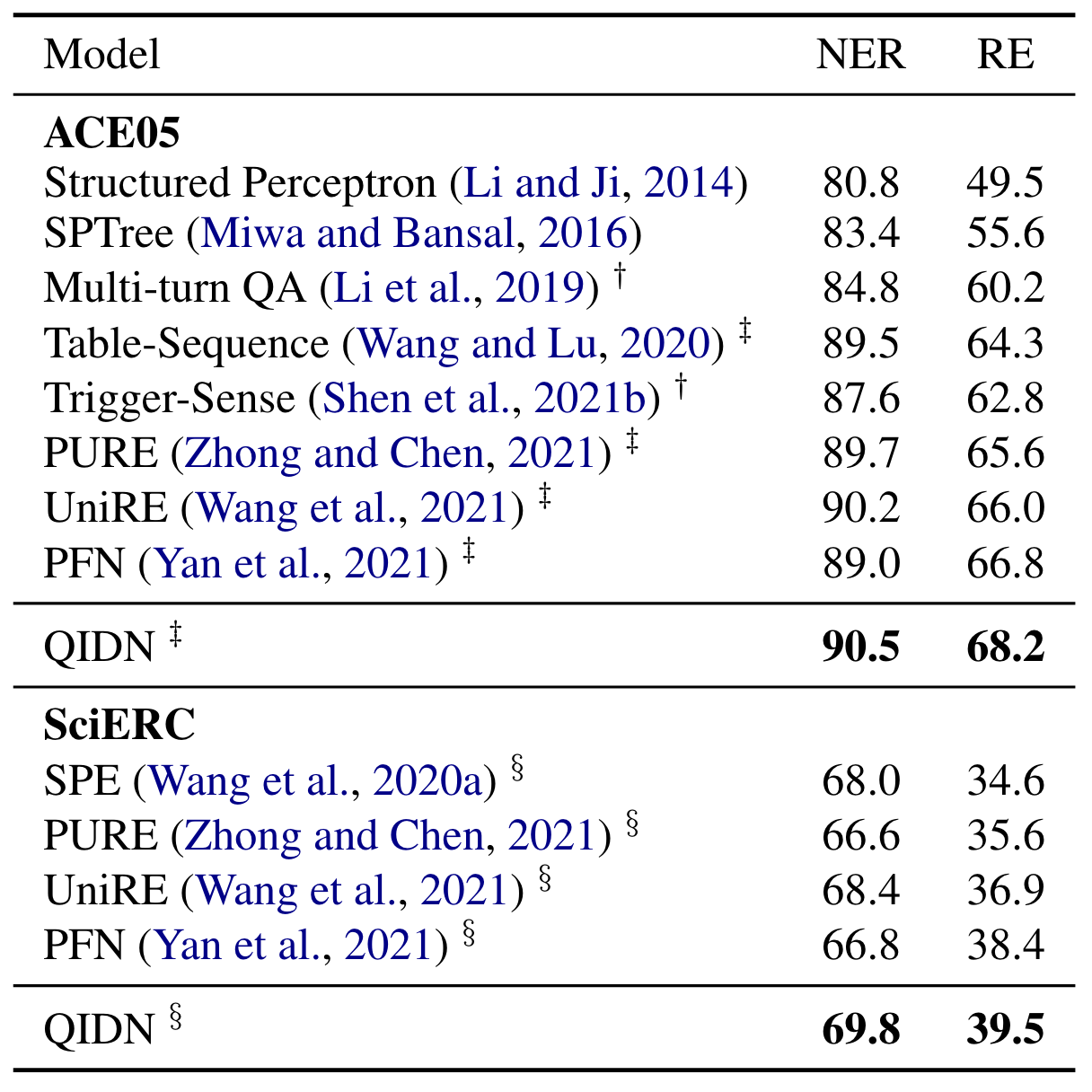
这里的RE的实验结果均为严格标准, 即要求实体类型, 关系类型, 实体边界均正确时的F1. QIDN也取得了SOTA, 相较于之前的一些Table Filling based模型比如UniRE, PFN都有明显的提升.

Analysis on Complex Scenarios

QIDN在NYT*和WebNLG*复杂场景表现如下:

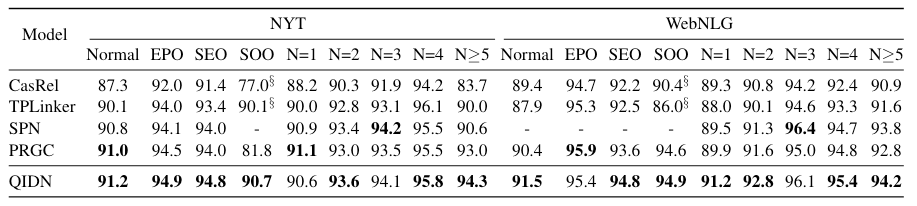
根据Baseline来看, QIDN对于三元组数量比较多的情况似乎比较擅长, 有比较明显的提升, 对于一般三元组的情况抽取进步也比较大.

Ablation Study

作者尝试了以下设定:

w/o $H_{span}$: 将Span Level表示替换为Token Level表示.
w/o $Q_e, Q_r$: 去掉对实体和关系Query的特化, 统一用同一种Query来代替.
w/o $\mathcal{L}_{ins}$: 去掉Instance Pair之间的对比学习Loss.
w/o $\mathcal{L}_{cls}$: 去掉Instance和Relation Embedding之间的对比学习Loss.
w/o $\mathcal{L}_{ins}, \mathcal{L}_{cls}$: 去掉所有对比学习Loss.

实验结果如下:

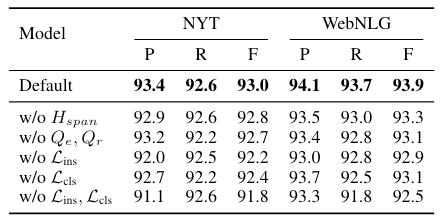
从中观察到, 影响比较大的是对比学习的两个Loss, 无论移除哪个都会产生较大的性能衰减. 将Query兵分两路也可以带来一些提升. Span Level的表示对WebNLG来说影响较大.

Topology of Relations

在NYT上对Relation Embedding经过L2正则化后用PCA的可视化如下:

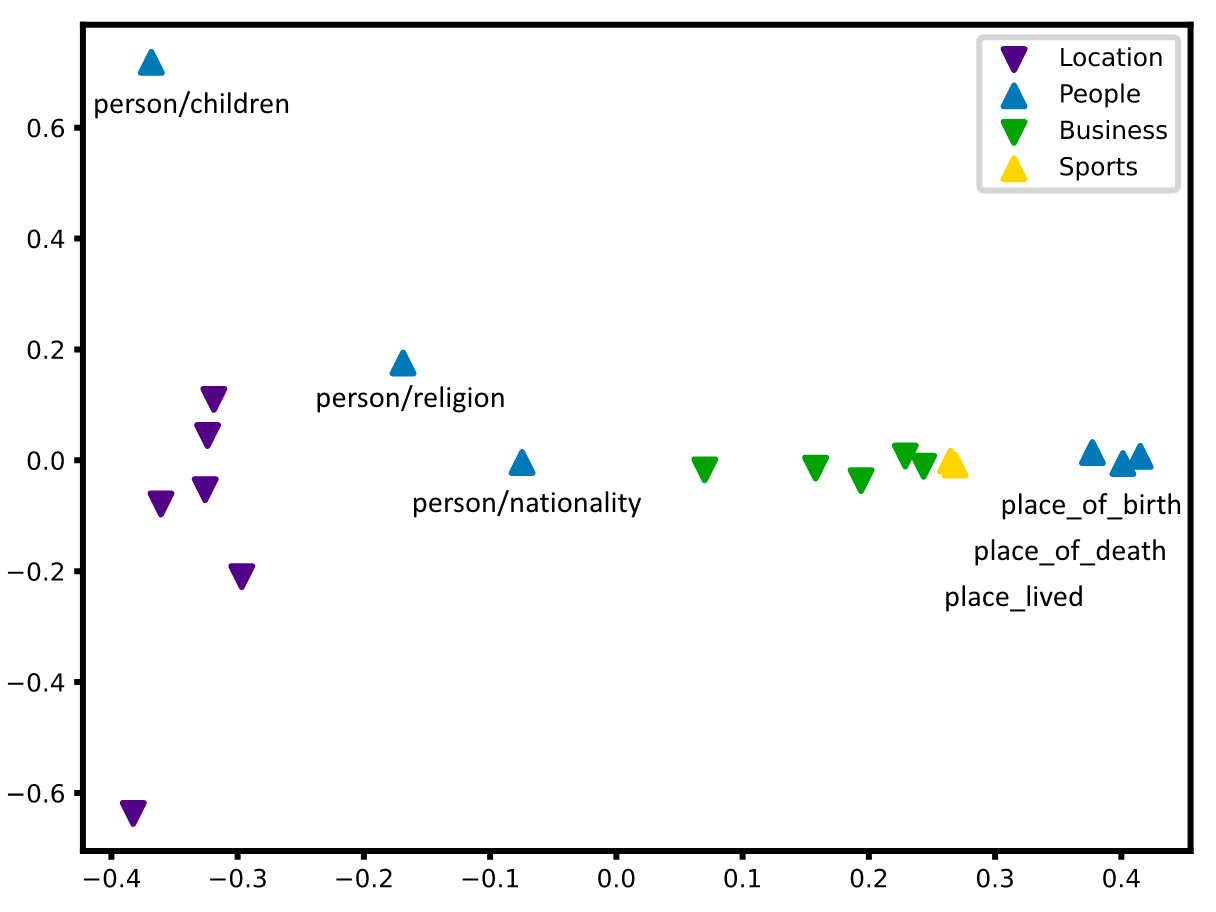
语义相近的关系嵌入都比较靠近. 与person相关的几个关系, 语义差别较大, 距离也比较远.

Error Analysis

作者将错误按NER和RE任务划分:

NER: ECE(Entity Classification Error), ELE(Entity Localtion Error).
RE: RCE(Relation Classification Error), PCE(Entity-Pair Classification Error), PLE(Entity-Pair Location Error).

在ACE05和SciERC这两个数据集上测试集错误比例如下:

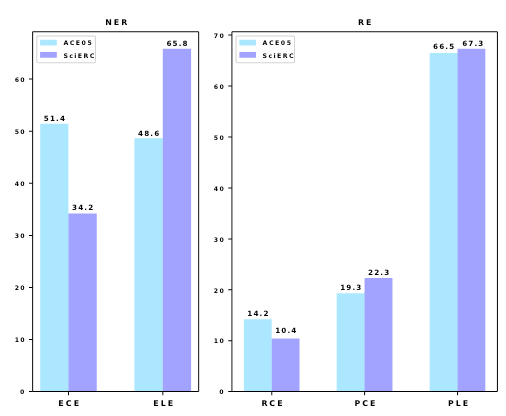
最高的是实体识别相关的ELE和PLE, 对关系分类RCE和PCE错误不明显, 证明了作者方法的有效性.

Summary

QIDN用Query based方法, 从Instance Level的角度解决了RE任务. 将Instance Query拆分为Relation Query和Entity Query两个branch从而将Query对应的三元组抽取出来, 同时在空间中用对比学习约束三元组, 使得三元组之间存在全局关联, 并捕获了关系的语义信息.

说真的, 自上次SPN以来, 已经有很长时间没有看到Query based Method在联合抽取上的模型了. 可惜代码没有开源.