UniRel: Unified Representation and Interaction for Joint Relational Triple Extraction
本文是论文UniRel: Unified Representation and Interaction for Joint Relational Triple Extraction 的阅读笔记和个人理解, 论文来自EMNLP 2022.
Basic Idea
作者认为现有的RTE模型存在下述两个缺点:
- 实体表示和关系表示是异质的.
- 异质的建模了实体 - 实体间交互和实体 - 关系间交互.
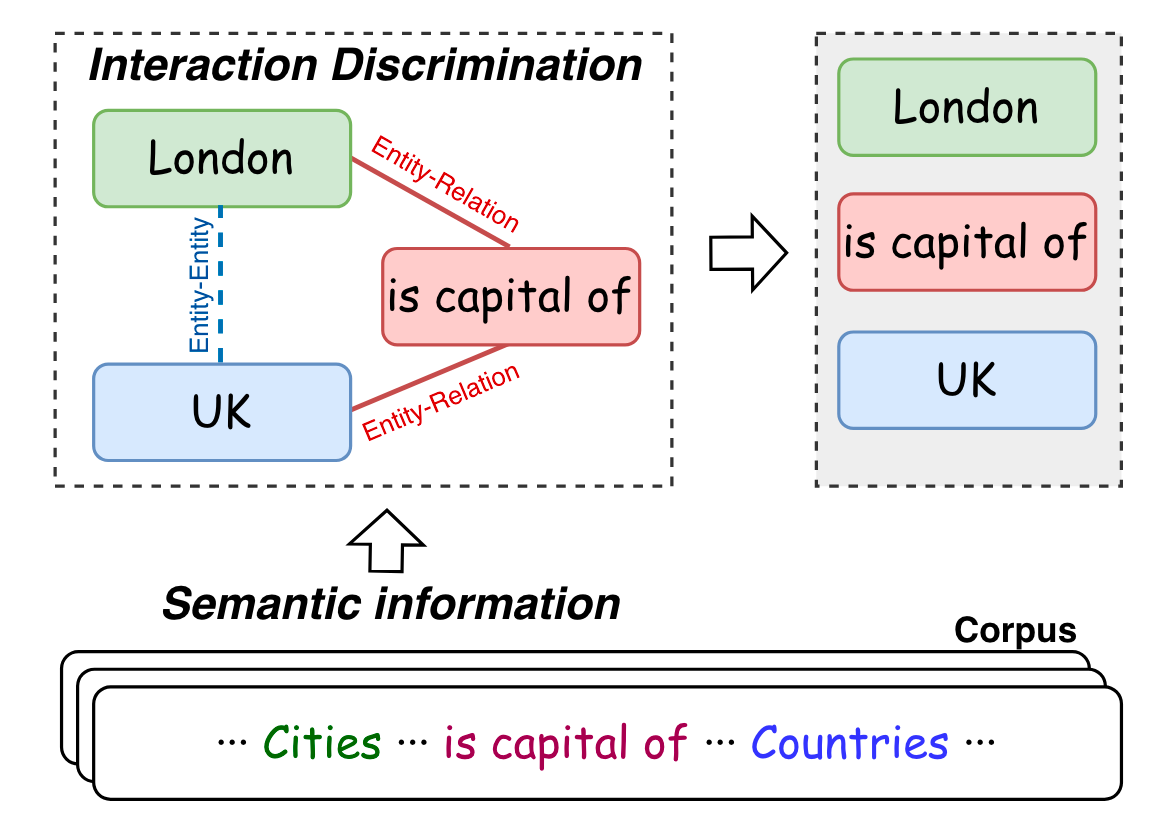
因此, 作者尝试统一关系与实体的表示类型, 并同时对二者做同质交互建模.
UniRel
Problem Formulation
对于给定的$N$ 个Token的句子$X=\set{x_1, x_2, \dots, x_N}$, 联合关系三元组抽取的目标是找到句子$X$ 中所有的三元组$T=[(s_l, r_l, o_l)]^L_{l=1}$, 其中$s_l, o_l, r_l$ 分别为Subject, Object和它们之间的关系, $L$ 为句子中的三元组总数.
关系来自于预定义好的集合$R=\set{R_1, R_2, \dots, R_M}$, $M$ 为关系类型数量.
Unified Representation
在作者的方法中, 将关系以它的实际语义Token引入进来, 比如说关系/business/company/founders 被手动的用founders代替.
然后以它们Embedding的形式当做关系表示:
$$
\begin{gathered}
T=\operatorname{Concat}\left(T_s, T_p\right) \\
H=E[T]
\end{gathered}
$$
其中$H \in \mathbb{R}^{(N+M) \times d_h}$ 为输入到BERT的向量, $d_h$ 为隐层维度, $T_s, T_p$ 分别为输入句子的Token ID和关系的Token ID.
这种方法其实可以看做是一种Prompt的应用, 附录中有关于作者对手动选择关系Token(Prompt) 的分析.
另外, 这里其实有一个小细节, 作者用BERT中的Segment Embedding(也就是Token Type Embedding)来区分实体和关系的Token.
接着用Self Attention来捕捉这些所有输入词之间的关系:
$$
\operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d_h}}\right) V
$$
其中$Q, K, V$ 分别是由$H$ 得到的Query, Key, Value向量.
Unified Interaction
由于作者认为异质建模实体和关系, 以及它们之间的交互, 是存在问题的. 所以作者尝试将它们的建模完全统一, 可以用如下交互图概括:
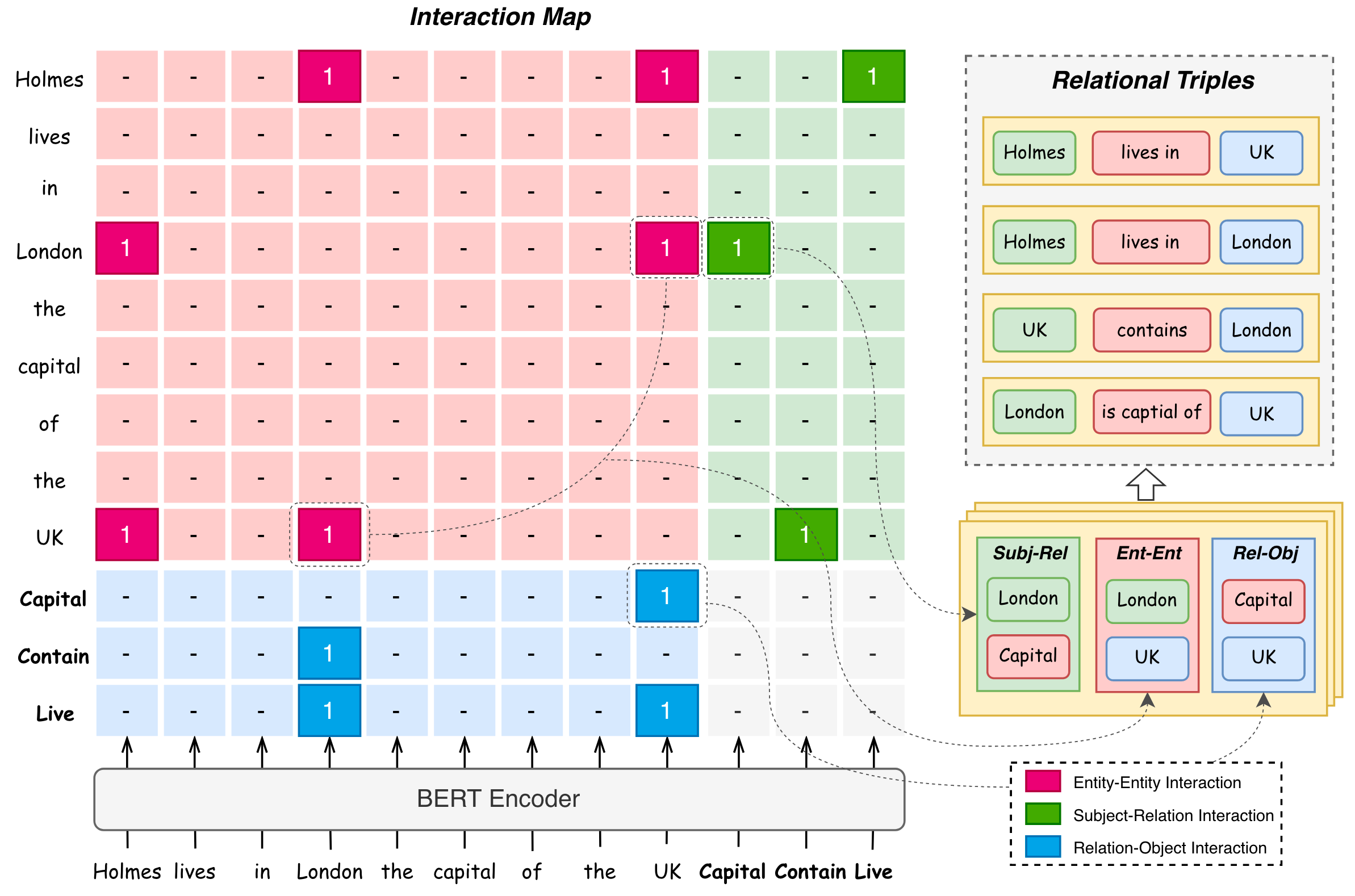
作者说明了表格中这三种区域表述的实际意义:
- 红色区域:
Entity - Entity Interaction. - 绿色区域:
Subject - Relation Interaction. - 蓝色区域:
Relation - Object Interaction.
交互图上的1便是行Token与列Token应该发生交互.
从直观上来看, 这种设计实际上是将关系三元组拆分为若干条边来进行解码.
Entity - Entity Interaction
对于句子$X$ 中的两实体$e_a, e_b$ 形成的实体对$(e_a, e_b)$ 而言, 当它们之间存在某种关系$r$ 时, 两实体之间才会产生交互.
形式上来说, 实体 - 实体间是否交互的符号函数为:
$$
I_e\left(e_a, e_b\right)= \begin{cases}\text { True } & \left(e_a, r, e_b\right) \in T \text { or } \\\ & \left(e_b, r, e_a\right) \in T, \exists r \in R \\\ \text { False } & \text { otherwise }\end{cases}
$$
由于$I_e(e_b, e_a) = I_e(e_a, e_b)$, 所以它是对称的.
Entity - Entity Interaction建模了实体之间的对齐关系(实体之间的成对关系).
Entity - Relation Interaction
实体 - 关系交互仅当实体存在某关系时才会发生. 即无论实体$e$ 拥有关系$r$ 时自身的角色是Subject $s$ 还是Object $o$ 都应该产生交互.
实体关系间是否产生交互的符号函数形式如下:
$$
\begin{aligned}
& I_r(e, r)= \begin{cases}\text { True } & (e, r, o) \in T, \exists o \in E \\
\text { False } & \text { otherwise }\end{cases} \\
& I_r(r, e)= \begin{cases}\text { True } & (s, r, e) \in T, \exists s \in E \\
\text { False } & \text { otherwise }\end{cases}
\end{aligned}
$$
由于关系是有向的, 所以实体 - 关系间交互是反对称的.
这种实体关系间交互的建模方式将表填充中的空间复杂度由$O(N\times M \times N)$ 优化到了$O((N+M)^2)$.
Interaction Discrimination
将BERT最后一层每个头$t$所生成的$Q_t, K_t$ 缩放点积后的结果取平均, 然后直接用Sigmoid做激活作为最终结果:
$$
\mathbf{I}=\operatorname{sigmoid}\left(\frac{1}{T} \sum_t^T \frac{Q_t K_t^T}{\sqrt{d_h}}\right)
$$
其中$\mathbf{I} \in \mathbb{R}^{(N+M)(N+M)}$ 是交互图中的交互矩阵, $T$ 是Self Attention头的数量, $W_t^Q, W_t^K$ 是可训练权重, 当$\mathbf{I}(\cdot)$ 超过阈值$\sigma$ 时, 认为该位置对应的行列Token存在交互.
在作者设计的交互图中, 只需要算个$Q, K$ 之间的相似度得分就可以了, 不需要重新获得表格表示, 索性丢掉后面的步骤, 用$Q, K$ 就行了.
另外, 其实从模型角度来看, 整个模型没有引入任何的额外参数… 对… 没有引入任何的额外参数.
Training and Decoding
Loss Function
作者的方法采用一张二元交互图就可以将三元组全部抽取出, 因此Loss采用二分类交叉熵即可:
$$
\begin{aligned}
\mathcal{L}=-\frac{1}{(N+M)^2} \sum_i^{N+M} \sum_j^{N+M}\left(\mathbf{I}_{i, j}^\ast \log \mathbf{I}_{i, j}\right.
\left.+\left(1-\mathbf{I}_{i, j}^\ast\right) \log \left(1-\mathbf{I}_{i, j}\right)\right)
\end{aligned}
$$
$\mathbf{I}^\ast$ 为交互图矩阵中的Ground Truth.
Decoding
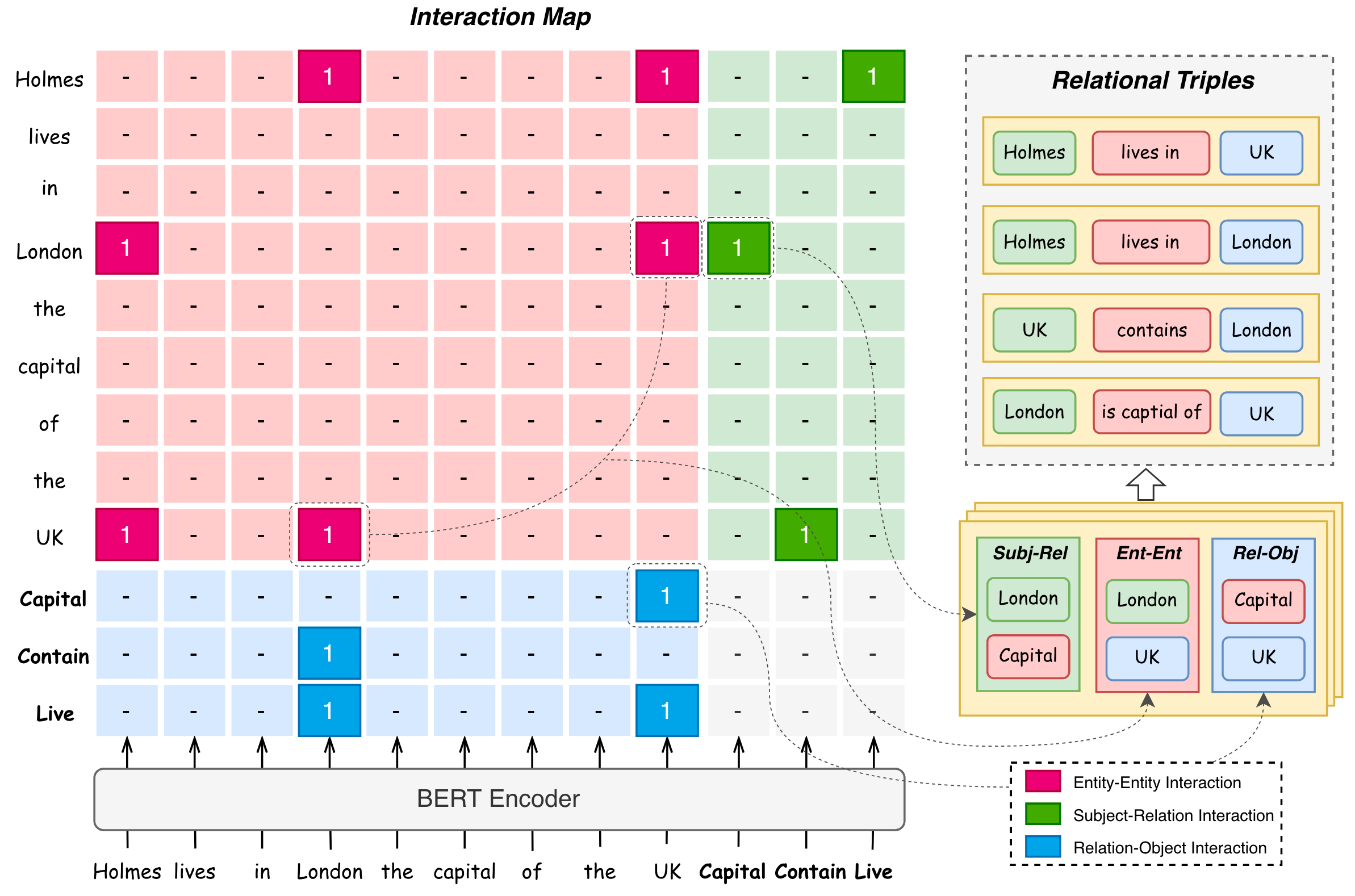
咱们直接拿交互图中的例子来说明解码流程:
- 根据右侧的绿色框框(Subj - Rel)和下面的蓝色框框(Rel - Obj)分别解码出每种关系$r$ 对应的Subject $e_i$ 和Object $e_j$. 即抽取出$(e_{i,}r), (r, e_j)$.
- 根据上一步找到的所有实体$e_i, e_j$, 穷举出所有的实体对$(e_{p}, e_q)$, 结合左上角的红色框框(Ent - Ent), 查看是否有对应的$(e_{p,}e_q)$ 为1.
- 如果在红色框框里有$(e_{p,}e_q)$ 为1, 则构成三元组$(e_{i},r, e_j)$. 即利用Subj - Rel $(e_{i},r)$, Ent - Ent $(e_{i,}e_j)$, Rel - Obj $(r, e_j)$ 共同形成三元组$(e_{i,}r, e_j)$.
例如, 在图中给出了一个既含有EPO又含有SEO的例子(在这里关系均使用语义Token代替):
- 首先从右侧的绿色框框拿到Subj - Rel, 有
(Holmes, Live),(London, Capital),(UK, Contain). - 从下面的蓝色框框拿到Rel - Obj, 有
(Capital, London),(Live, London),(Capital, UK),(Live, UK). - 然后穷举出所有的实体对, 并结合红色框框Ent - Ent进行检查, 有效的有
(Holmes, London),(Holmes, UK),(UK, London),(London, UK)这四个实体对. - 结合Subj - Rel, Rel - Obj, Ent - Ent, 可以解码出关系三元组. 比如, Subj - Rel有
(Holmes, Live), Rel - Obj有(Live, London), 同时Ent - Ent有(Holmes, London), 那么就可以解码出三元组(Holmes, Live, London). 与之类似的, 可以共同解码出(Holmes, Live, UK),(UK, Contain, London),(London, Capital, UK)这其他三个三元组.
Extended to Multi - token Entity Setting
如果上述方法去打标签, 会产生一个严重问题: 面对多Token实体要怎么办? 起初, 我认为该方法仅能在NYT和WebNLG的部分匹配数据集上生效.
后来我发现作者在附录中写到, UniRel实际上可以扩展到多Token实体. 具体的方法是:
- 将实体识别从单Token识别扩展为边界识别. 即先将一张交互图变为两张, 来分别完成
(Subject Head, Relation, Object Head)以及(Subject Tail, Relation, Object Head)的抽取. - 添加第三张关于每个实体的头尾交互图, 完成
(Head, Relation, Tail)的抽取. - 对于每个关系, 将实体的头尾Token链接起来, 作为一个实体, 然后像之前一样解码.
所以作者使用了三张交互图完成了单Token实体到多Token实体的转化.
Experiments
详细的参数设置请参照原论文.
Datasets
本论文所采用的实验数据集是NYT和WebNLG, 主要是二者的部分匹配版本:
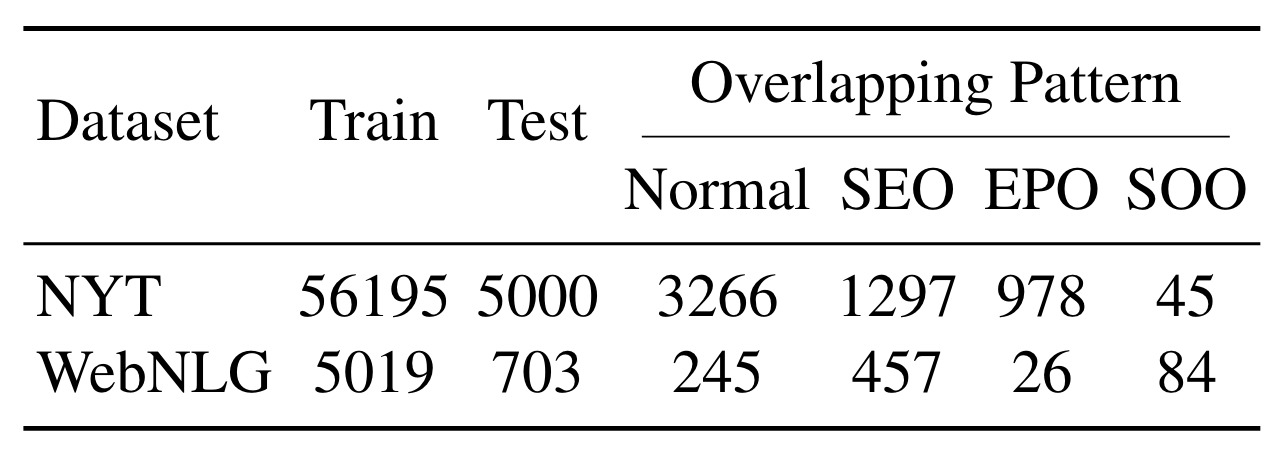
Results
在NYT和WebNLG的部分匹配上结果如下:
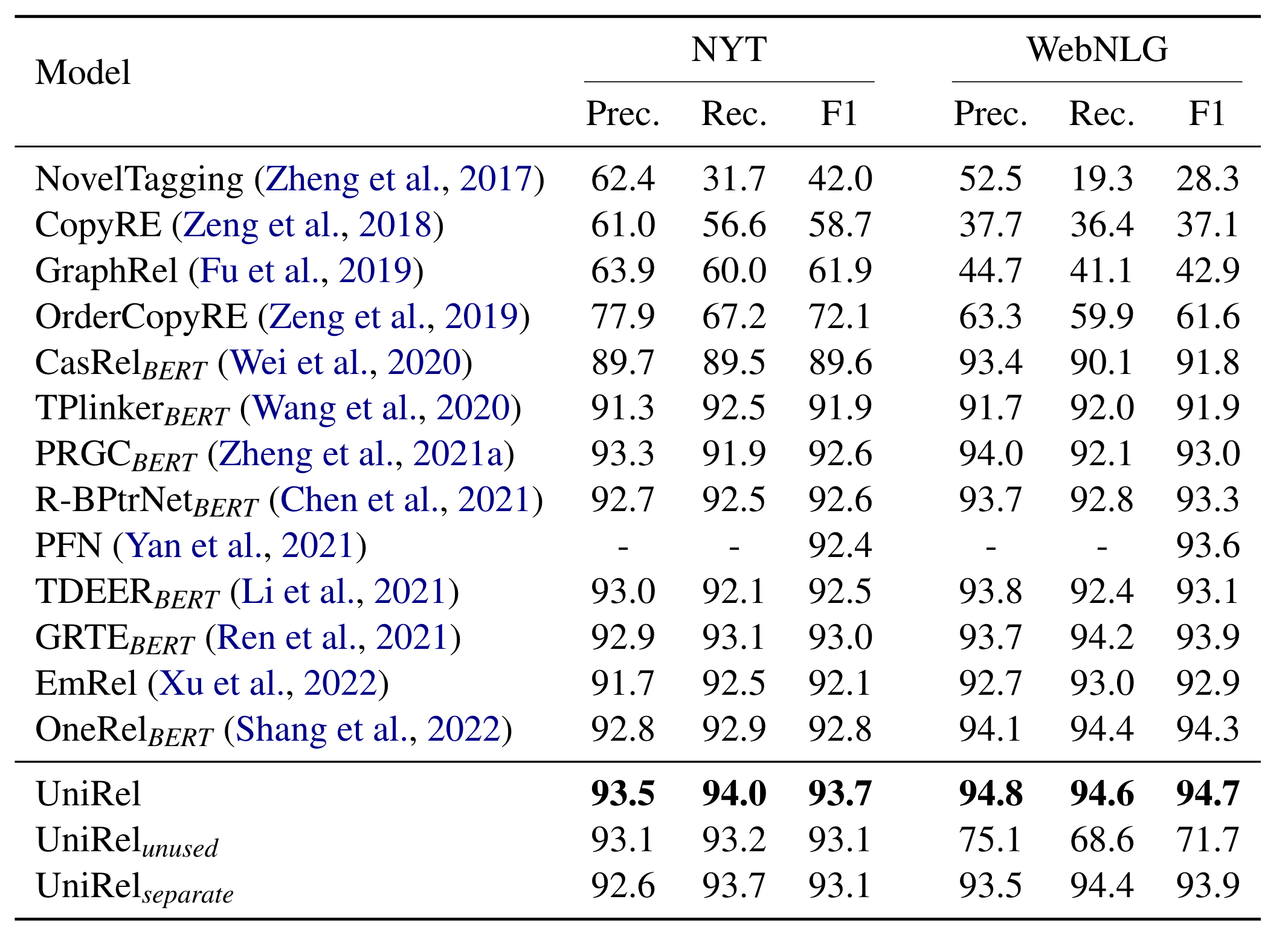
先全局的看一下结果, UniRel打败了OneRel成为了SOTA, 甚至WebNLG冲着95去了, NYT部分匹配也快能到94了.
这里面有两种额外设置:
- unused: 用BERT
[unused*]Token来代替每种关系的语义Embedding, 也就是重新训练一个随机初始化的关系Embedding. - separate: 用一个共享的BERT分别将输入的句子和关系语义Token编码, 然后用不同的两个Transformer Layer获得对应的Q和K, 再将Q, K分别拼接后做点积预测.
能够看到, 当把关系换到随机初始化的Embedding, 而不是它们的语义Token的Embedding后在WebNLG上效果骤降.
在原论文的附录中其实也有精准匹配的结果(多Token设置):
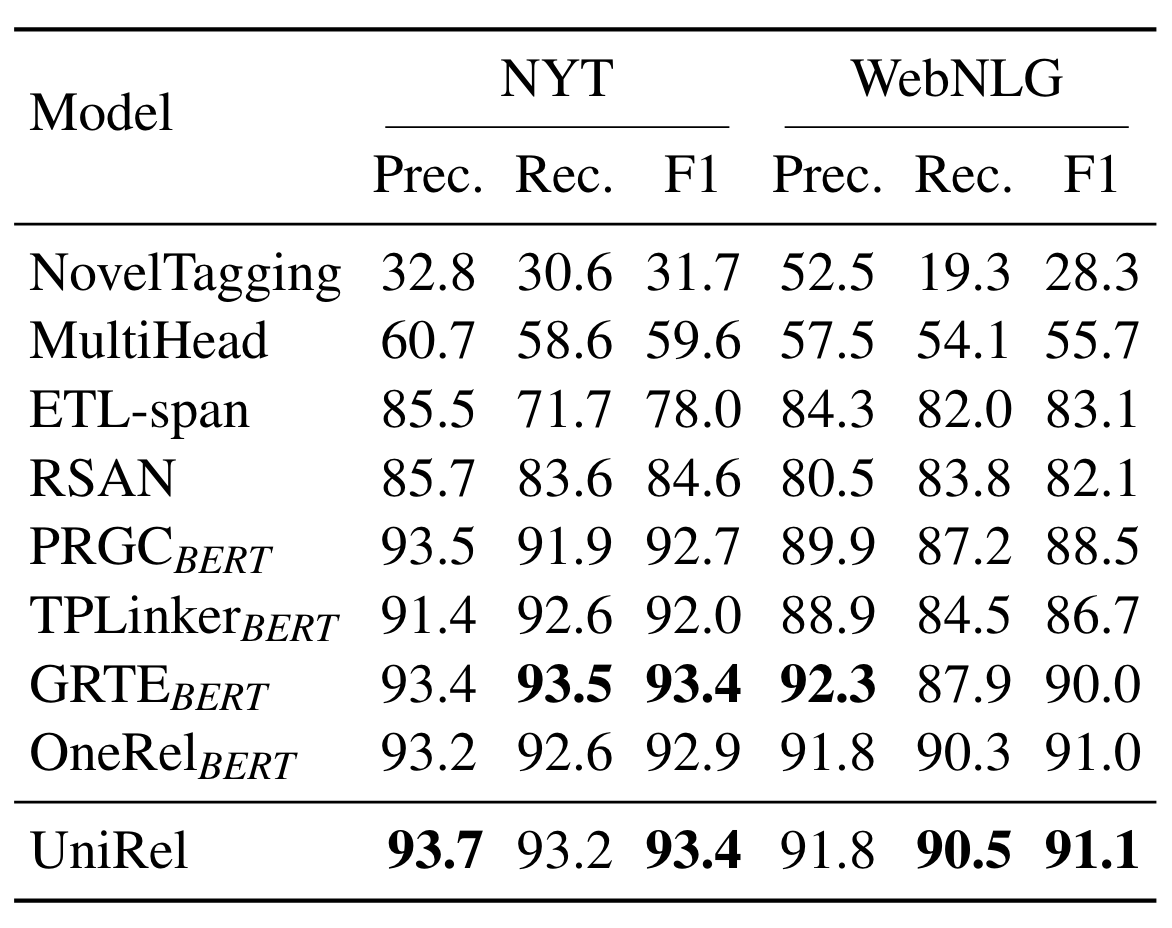
总的来说也是SOTA, 但是可能对比没有部分匹配的结果提升明显, 并且它使用了三张交互图, 所以就没有放到正文中.
在NYT*上的复杂场景下UniRel结果如下:
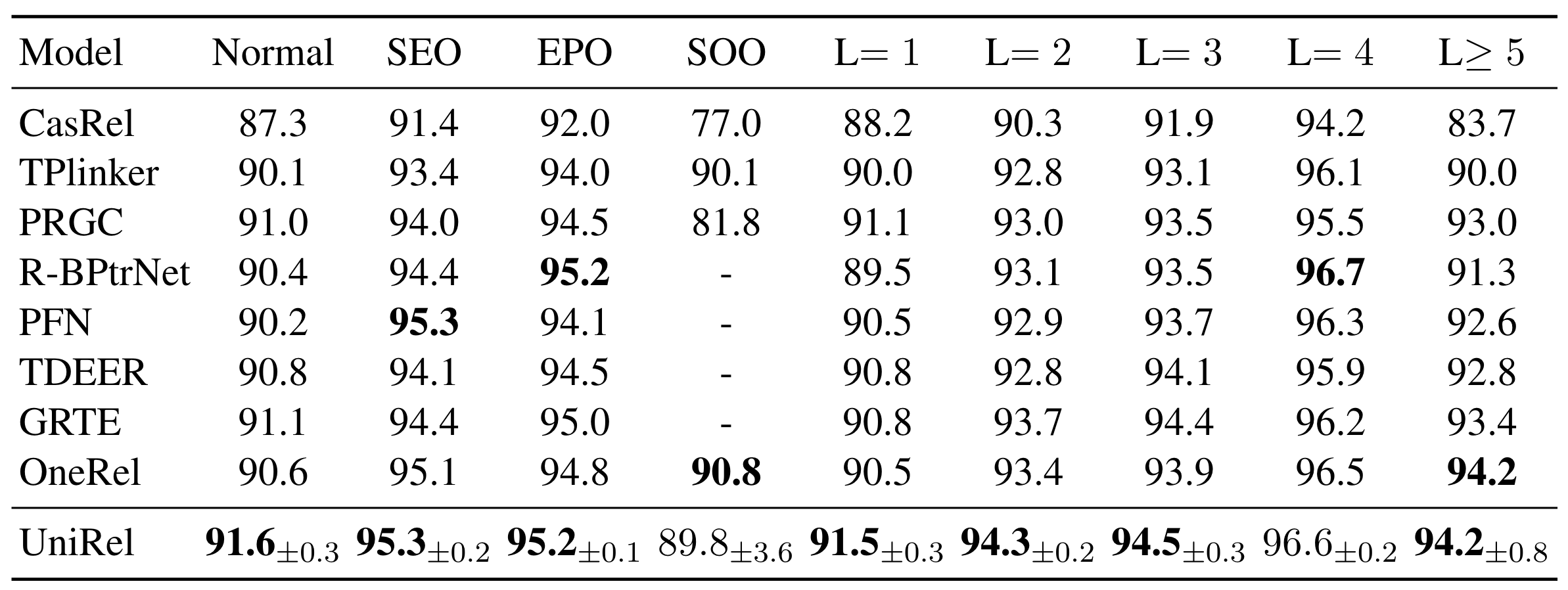
能够观察到比较明显的提升来自于识别Normal三元组(Normal三元组总体数量更多), 在更多三元组的句子中也有相较于别的模型比较大的提升.
而且从交叉验证来看, 作者的算法是比较稳定的. 现在少有还在做交叉验证的算法, 做了比较严谨.
Analysis
Effect of the Unified Representation
为了证明作者的统一表示建模有效, 所以作者采用了unused 设置(详见主实验结果), 发现在WebNLG上效果下降的非常厉害. 所以作者怀疑是WebNLG的数据所致, WebNLG中有更多的关系, 但是却只有更少的数据.
为了验证这个猜想, 作者统计了不同数量样本的关系下预测三元组的情况, 如下所示:
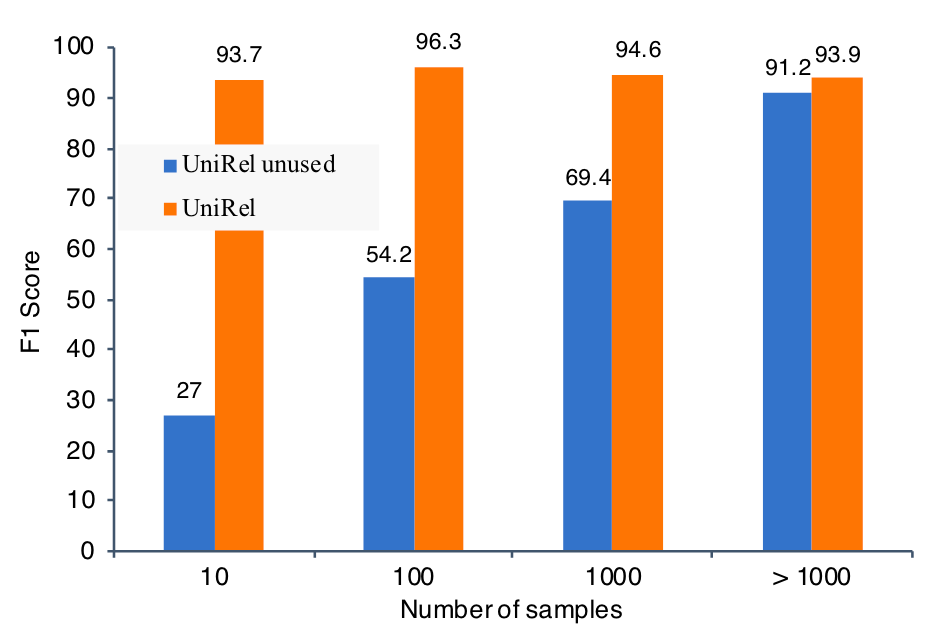
F1明显的在关系所对应的样本数量增大后提升, 但UniRel在融入了一定的语义信息后, 即使是在>1000条样本的设置下, 比unused 自由学习结果还是要好一些.
Effect of the Unified Interaction
为了证实作者建模的统一交互形式有效, 作者采用了sparate 设置. 在去掉了实体间交互和实体关系交互后, 效果有所下降.
作者分别测试了在两个数据集上的实体间交互和实体关系交互预测的准确率:
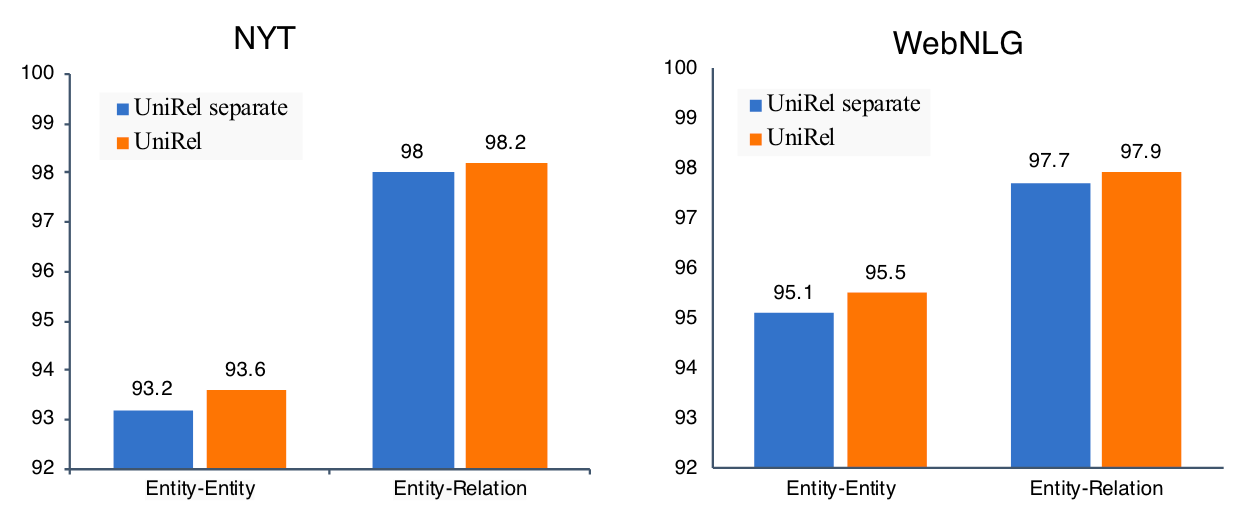
无论是哪个数据集, 分离的方式都不如同时交互的方式, 说明把它们都放在一个表下交互是有效的.
Computational Efficiency
作者对比了UniRel与前人方法中的训练时间和推理时间:
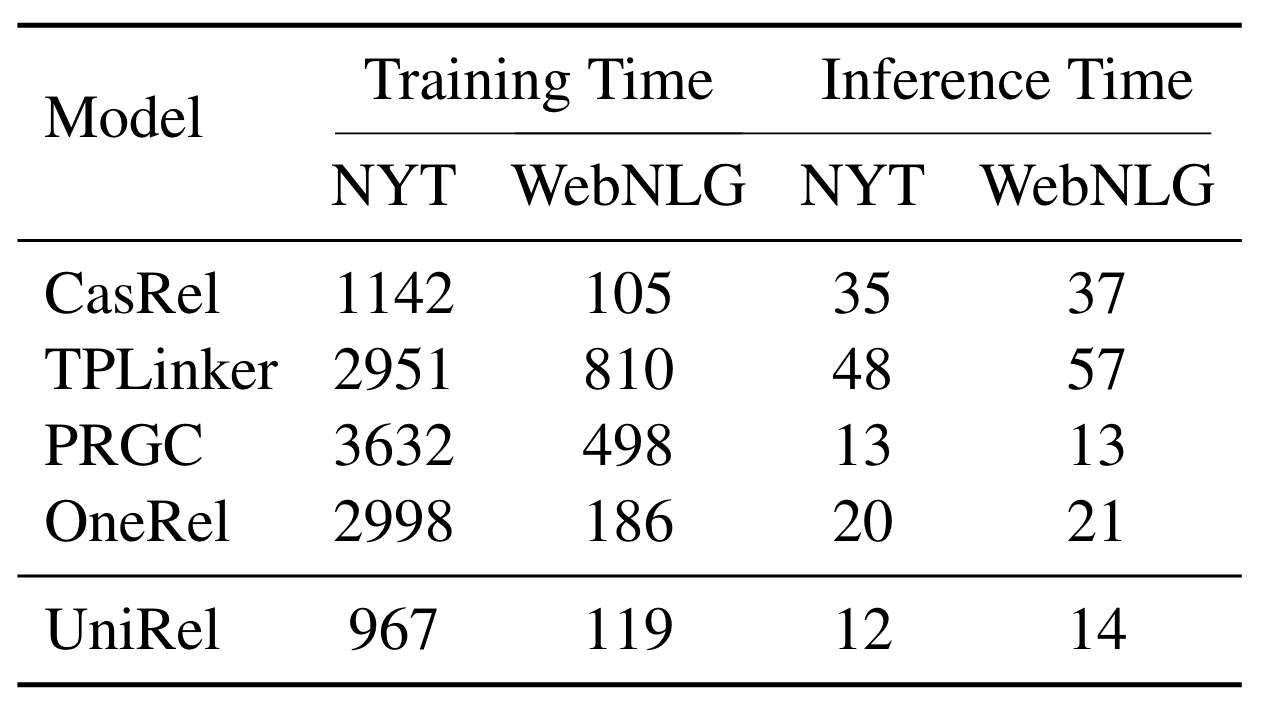
在将关系表数量减少后, 训练速度和推理速度都有了明显的提升, 那么空间复杂度实际上也从表填充方法的$O(N \times M \times N)$ 优化到了$O((N + M)^2)$.
Visualization
作者的表填充设计非常有意思, 所以可以做一个句子和关系语义拼在一起的可视化:
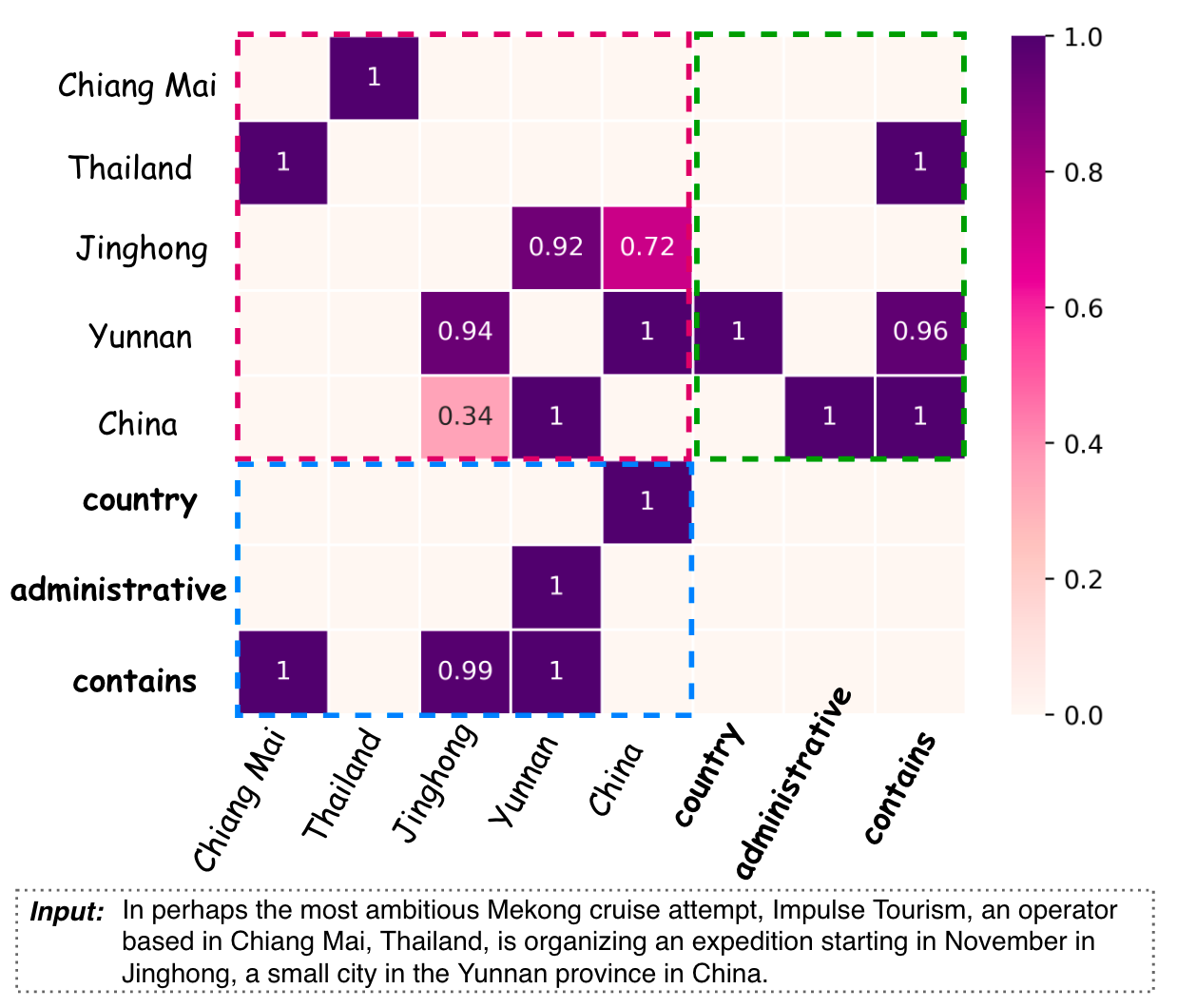
能看到图中的模型学的很好, 大多数置信度都非常高. 并且抽出了所有的六个三元组, 分别为(Yunnan, country, China), (China, administrative_divisions, Yunnan), (Thailand, contains, Chiang Mai), (Yunan, Contains, Jinghong), (China, Contains, Jinghong), (China, Contains, Yunnan).
其实从图中也能看出一些表填充设计上的鲁棒性,
(China, Jinghong)之间的三元组成立是通过主对角线两侧有任意一个超过阈值即可. 即使主对角线下面标成0.34了, 但是上面是0.72挽救了这一问题, 这点作者没有在原文中提到.在开源代码中, 分两次进行抽取, 分别抽取上三角和下三角, 所以在抽取上三角时, 0.72已经可以检测出
(China, Jinghong)存在关系, 不需要在意下三角是否抽取出.
Summary
UniRel是一种表填充式的RTE方法, 通过将关系转化为语义Token, 把实体和关系变成了统一表示方法, 并且做完全同质建模, 效果达到了目前任务上真正的SOTA.
效率是非常高的, 从$O(N\times M \times N)$ 优化到了$O((N+M)^2)$, 解决了表填充带来的关系表冗余的问题.
从实验上来看, 作者提出的算法还是比较稳定的, 并且具有一定的容错率.

