本文前置知识:
- RNN: 详见循环神经网络小结.
A Partition Filter Network for Joint Entity and Relation Extraction
本文是论文A Partition Filter Network for Joint Entity and Relation Extraction的阅读笔记和个人理解, 论文来自EMNLP 2021. 图片全部出自原论文和PPT. 本文为RTE问题中, 探讨NER和RE任务间关系的系列三部曲中的第三篇.
Basic Idea
在先前的联合抽取任务中, 人们少有考虑NER和RE任务间的关系.要么是以Pipeline的形式做NER和RE, 导致任务间的特征交互不平衡, 要么是并行的对NER和RE任务的特征分别编码, 导致特征构建很大程度上是相互独立的.
因此, 作者希望提出一种两路交互模型, 从多任务学习视角充分挖掘NER和RE两任务之间的关系, 保证二者之间信息的均衡传递, 在此基础上完成联合抽取任务.
PFN
PFN由LSTM改进而来, 有LSTM基础再理解会好一些.
Problem Formulation
首先联合抽取中的两个子任务NER, RE做出定义.
对于给定的长度为$L$ 的输入序列$s=\set{w_1, \dots, w_L}$:
- NER的任务目标是在给定实体起始Token$w_i$ 和结束Token$w_j$ 的情况下, 抽取出标有类别的实体$e \in \mathcal{E}$ , $\left\langle w_{i}, e, w_{j}\right\rangle \in S$.
- RE的任务目标是在给定Subject的起始Token $w_i$ 和Object的起始Token$w_j$ 的情况下, 抽取出二者存在的关系$r \in \mathcal{R}$, 即$\left\langle w_{i}, r, w_{j}\right\rangle \in T$, $T$ 为三元组.
从形式上观察, NER和RE这两个任务都可以仅由实体的Span完成, 它们从形式上是保持一致的. 只不过NER要求的Span同属于同一个实体, 而RE的Span一个来自于Subject, 另一个来自于Object.
Partition Filter Encoder
PFN的Ecndoer就是被改进过的LSTM, 作者在LSTM基础上增加了Partition和Filter机制, 使得两任务之间的信息能够均衡合理的传递.
Partition
NER和RE之间存在很强的关联, 但每个任务也同样应该有自己独立的特征, 这部分独立特征是不该被另一个任务所影响的. 划分(Partition)机制的目标就是要学习到仅与本任务相关联的特征位置.
并不是所有特征全部共享就好, 而是只共享该共享的. 这看起来是一句废话, 但在多任务学习(Multi Task Learning, MTL) 中很常见, 也很重要. 若共享了不该共享的部分, 对每个任务的完成可能都有害.
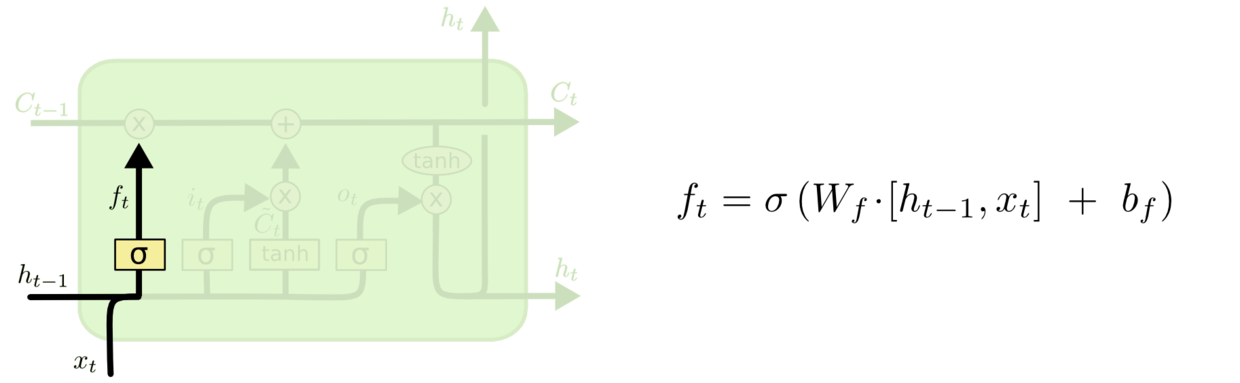
先从LSTM的细胞状态入手, 当前时刻$t$ 的初始细胞状态$\tilde{c_t}$ 由当前时刻输入$x_t$ 和上个时刻的记忆$h_{t-1}$ 共同决定:
$$
\tilde{c}_{t}=\tanh \left(\operatorname{Linear}\left(\left[x_{t} ; h_{t-1}\right]\right)\right)
$$
这点与LSTM的输入门得到$\tilde{C}_t$ 的方式保持一致:
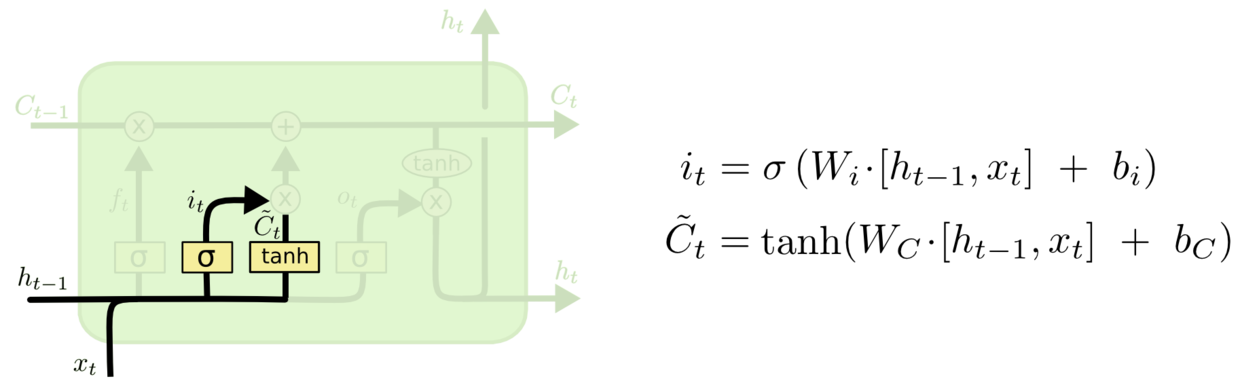
接着, 作者希望使用门控机制, 使得两个任务能够找到独属于自己的那部分特征划分. $\text{cummax}$ 可以完成划分的这个动作.
$$
\operatorname{cummax}(\cdot)=\operatorname{cumsum}(\operatorname{softmax}(\cdot))
$$
其中, $\text { cumsum }$ 为作者自定义的函数:
$$
\begin{gathered}
\text { cumsum }\left(x_{1}, x_{2}, \ldots, x_{n-1}, x_{n}\right)=\left(x_{1}, x_{1}+x_{2}, \ldots,\right. \\
\left.x_{1}+x_{2}+\cdots+x_{n-1}, x_{1}+x_{2}+\cdots+x_{n-1}+x_{n}\right)
\end{gathered}
$$
每个位置上的返回值为输入的对应位置元素及之前元素的和, 亦或许可以写做:
$$
\begin{gathered}
\text { cumsum }\left(x_{1}, x_{2}, \ldots, x_{n-1}, x_{n}\right)=\left(\sum^1_{n=1}x_i, \sum^2_{n=1}x_i,\sum^{n-1}_{n=1}x_i,\cdots, \sum^n_{n=1}x_i\right)
\end{gathered}
$$
$\text{cummax}$ 的输出值可以近似成一个二进制向量$(0, \cdots, 0, 1, \cdots, 1)$. 举个栗子:
$$
\begin{aligned}
x &= (0.1, 0.1, 0.6, 0.1, 0.1) \\
\text{cumsum}(x) &= (0.1, 0.2, 0.8, 0.9, 1.0) \\
&\approx (0, 0, 1, 1, 1)
\end{aligned}
$$
NER和RE这两个任务都各有一个对输入划分的门控剪刀, 把输入分为任务相关, 任务不相关两块. 这两把剪刀分别记为$\tilde{e}$ 和$\tilde{r}$:
$$
\begin{aligned}
&\tilde{e}=\operatorname{cummax}\left(\operatorname{Linear}\left(\left[x_{t} ; h_{t-1}\right]\right)\right) \\
&\tilde{r}=1-\operatorname{cummax}\left(\operatorname{Linear}\left(\left[x_{t} ; h_{t-1}\right]\right)\right)
\end{aligned}
$$
该设计使得NER和RE任务都有独属于自己的部分.
注意, 这两个$\text{Linear}$ 的参数是不一样的. 对于同一组输入, $\tilde{e}$ 和$\tilde{r}$ 可能得到一块交叉的区域, 这也就是共享区域, 该区域是由两个门控共同决定的.
两刀切三份, 接下来就把两把剪刀切出来的结果表示出来.
这里给出的是上个时刻$t-1$ 的划分$\rho_{c_{t-1}}$, 因为在LSTM中, 后面要借助$t-1$ 时刻表达当前时刻$t$ 对应的划分:
$$
\begin{aligned}
\rho_{s, c_{t-1}} &=\tilde{e}_{c_{t-1}} \circ \tilde{r}_{c_{t-1}} \\
\rho_{e, c_{t-1}} &=\tilde{e}_{c_{t-1}}-\rho_{s, c_{t-1}} \\
\rho_{r, c_{t-1}} &=\tilde{r}_{c_{t-1}}-\rho_{s, c_{t-1}}
\end{aligned}
$$
$\tilde{e}, \tilde{r}$ 的结果做逐元素点乘, 就能获取共享部分, 细胞状态被切成了三份: NER区, RE区, Share区:
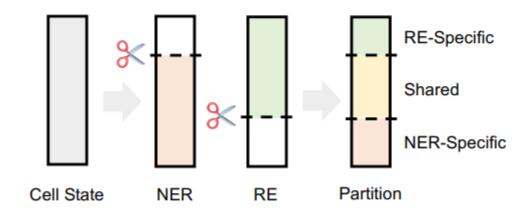
对于三个式子, PPT中给出了一个例子. 若$\tilde{e}=(0, 1, 1), \tilde{r} =(1, 1, 0)$, 则有:
$$
\begin{aligned}
\rho_{s, c_{t-1}} &= (0,1,1) \circ (1,1,0)=(0,1,0)\\
\rho_{e, c_{t-1}} &= (0,1,1)- (0,1,0)=(0,0,1)\\
\rho_{r, c_{t-1}} &= (1,1,0)- (0,1,0)=(1,0,0)
\end{aligned}
$$
对于NER, RE, Share区, 每个区域划分到的细胞状态$\rho$ 都由上个时刻的对应区域的细胞状态$c_{t-1}$ 和当前时刻对应区域的初始细胞状态$\tilde{c_t}$ 共同决定:
$$
\begin{aligned}
\rho_{e} &=\rho_{e, c_{t-1}} \circ c_{t-1}+\rho_{e, \tilde{c}_{t}} \circ \tilde{c}_{t} \\
\rho_{r} &=\rho_{r, c_{t-1}} \circ c_{t-1}+\rho_{r, \tilde{c}_{t}} \circ \tilde{c}_{t} \\
\rho_{s} &=\rho_{s, c_{t-1}} \circ c_{t-1}+\rho_{s, \tilde{c}_{t}} \circ \tilde{c}_{t}
\end{aligned}
$$
$\rho$ 并不是PFN Encoder最终的细胞状态, 上述过程仅是与LSTM中的细胞状态更新相似:

作者认为, 把细胞状态拆为三个区域, 再将它们合起来, 和不划分时不是等价的, 会损失一部分信息, 这个机制与LSTM的遗忘门类似:
这种解释还是非常巧妙的, 不需要在模型中显式设计出遗忘门.
Filter
在上个阶段Partition对输入区域完成了划分, 在本阶段将对每个任务所需特征做表征重组.
首先把上阶段得到的三部分组装在一起, 对应区域得到新的记忆$\mu$.
NER可以使用独有的细胞状态$\rho_e$ 和共享细胞状态$\rho_s$, RE可以使用独有细胞状态$\rho_r$ 和共享细胞状态$\rho_s$, 对任务无关的信息直接被滤去:
$$
\begin{aligned}
\mu_{e}&=\rho_{e}+\rho_{s} \\\
\mu_{r}&=\rho_{r}+\rho_{s}\\
\mu_{s}&=\rho_{s}
\end{aligned}
$$
然后给记忆$\mu$ 激活一下子:
$$
\begin{aligned}
&h_{e}=\tanh \left(\mu_{e}\right) \\
&h_{r}=\tanh \left(\mu_{r}\right) \\
&h_{s}=\tanh \left(\mu_{s}\right)
\end{aligned}
$$
$h$ 将作为特定任务的表示, 在解码过程中使用.
最后就是PFN Encoder的更新细胞状态$c_t$, 并由$c_t$ 得到当前时刻隐态$h_t$, 完成输出过程:
$$
\begin{aligned}
c_{t} &=\operatorname{Linear}\left(\left[\mu_{e, t} ; \mu_{r, t} ; \mu_{s, t}\right]\right) \\
h_{t} &=\tanh \left(c_{t}\right)
\end{aligned}
$$
这与LSTM的输出门相似, 但又不太一样:
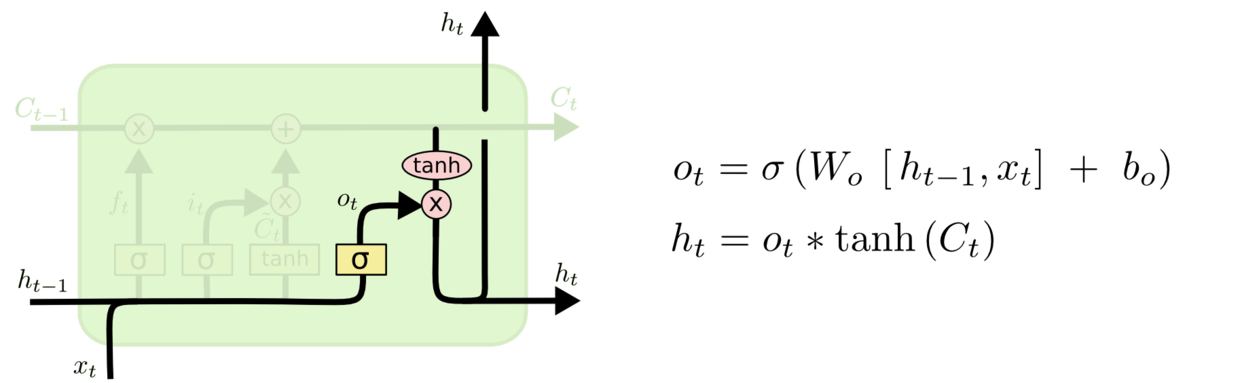
至此, PFN Encoder信息流可以由下图概括:
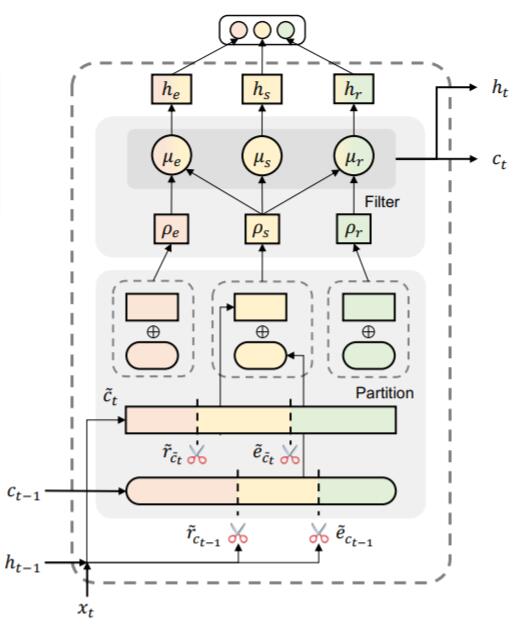
只是看输入和输出, 相较于LSTM仍然没有变化, 信息流为:
- 上时刻$t-1$ 被划分好的三份的细胞状态(NER区, RE区, Share区)记为$\rho_{c_{t-1}}$, 与当前时刻划分好的三份初始细胞状态$\rho_{\tilde{c}_t}$, 生成$t$ 时刻划分好的新细胞状态$\rho$.
- 新细胞状态进一步过滤得到任务特化的细胞状态$\mu$.
- 激活后得到任务所需的表征$h_e, h_r, h_s$.
- 用类似输出门的方式得到当前时刻$t$ 的最终细胞状态$c_t$, 和输出隐态$h_t$.
Global Representation
因为作者使用的是单向编码器, 只有前向(Forward)而没有反向(Backward), 所以这里作者用提取的全局特征$h_{g}$ 来代替反向编码所获取的信息:
$$
\begin{aligned}
h_{g_{e}, t}=\tanh \left(\operatorname{Linear}\left[h_{e, t} ; h_{s, t}\right]\right) \\
h_{g_{r}, t}=\tanh \left(\operatorname{Linear}\left[h_{r, t} ; h_{s, t}\right]\right) \\
h_{g_{e}}=\operatorname{maxpool}\left(h_{g_{e}, 1}, \ldots, h_{g_{e}, L}\right) \\
h_{g_{r}}=\operatorname{maxpool}\left(h_{g_{r}, 1}, \ldots, h_{g_{r}, L}\right)
\end{aligned}
$$
最后用了一个最大池化, 只保留整个句子中最重要的信息, 作为全局表示.
Task Units
Task Unit也就是Decoder, 采用朴实无华的Table Filling Decoding策略. 因为前面观察过NER和RE任务的形式一致, 均可视为二分类问题, 仅依赖于两两Token就能完成实体类别和关系类别的判定, 所以两个任务的解码单元也可以设计得一样.
NER Unit
每个实体类型$k$ 都有一张表, 在$k$ 表中第$i$ 行第$j$ 列被填上的值为, 类型为$k$ 的实体起始Token为$w_i$, 结束Token为$w_j$ 的概率$e_{ij}^k$, 由$h_i^e, h_j^e$, 以及全局表示$h_{g_e}$ 拼接后变换得到:
$$
\begin{aligned}
h_{i j}^{e}&=\operatorname{ELU}\left(\operatorname{Linear}\left(\left[h_{i}^{e} ; h_{j}^{e} ; h_{g_{e}}\right]\right)\right)\\
e_{i j}^{k} &=p\left(e=\left\langle w_{i}, k, w_{j}\right\rangle \mid e \in S\right) \\
&=\sigma\left(\operatorname{Linear}\left(h_{i j}^{e}\right)\right), \forall k \in \mathcal{E}
\end{aligned}
$$
RE Unit
RE单元可以由NER单元如法炮制. 每个关系类型$l$ 都有一张表, 在$l$ 表中第$i$ 行第$j$ 列被填上的值为, Token为$w_i$ 的Subject和起始Token为$w_j$ 间存在关系$l$ 的概率$r_{ij}^l$ , 同样由两Token间表示$h_i^r, h_j^r$, 以及全局表示$h_{g_r}$ 拼接, 后经过激活, 变换得到:
$$
\begin{aligned}
h_{i j}^{r} &=\operatorname{ELU}\left(\operatorname{Linear}\left(\left[h_{i}^{r} ; h_{j}^{r} ; h_{g_{r}}\right]\right)\right) \\
r_{i j}^{l} &=p\left(r=\left\langle w_{i}, l, w_{j}\right\rangle \mid r \in T\right) \\
&=\sigma\left(\operatorname{Linear}\left(h_{i j}^{r}\right)\right), \forall l \in \mathcal{R}
\end{aligned}
$$
Training and Inference
因为作者假定填表任务为二分类问题, 所以使用二分类交叉熵(BCE Loss)优化:
$$
\begin{aligned}
L_{n e r} &=\sum_{\hat{e}_{i j}^{k} \in S} \operatorname{BCELoss}\left(e_{i j}^{k}, \hat{e}_{i j}^{k}\right) \\
L_{r e} &=\sum_{\hat{r}_{i j}^{l} \in T} \mathrm{BCELoss}\left(r_{i j}^{l}, \hat{r}_{i j}^{l}\right)
\end{aligned}
$$
$\hat{e}_{i j}^{k}, \hat{r}_{i j}^{l}$ 为真实标签. 在推理时, 各实体, 关系存在的概率仅当均大于阈值$\lambda$ 时, 三元组$(s_{i, j}^k, l, o_{m, n}^{k\prime})$ 成立:
$$
e_{i j}^{k} \geq \lambda_{e} ; e_{m n}^{k^{\prime}} \geq \lambda_{e} ; r_{i m}^{l} \geq \lambda_{r}
$$
文中取阈值均为0.5.
PFN整体的模型框架图如下:
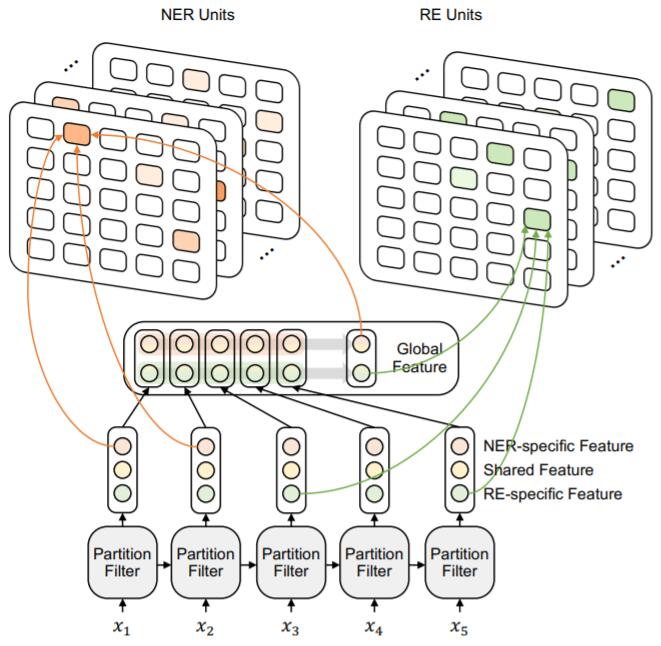
先由Partition Filter划分过滤得到任务特化的特征, 再提取整句全局特征, 最后结合二者通过两个简单的Task Unit二分类填表, 完成联合抽取.
Experiments
Main Results
在联合抽取常用的两个数据集NYT和WebNLG上, 效果如下:
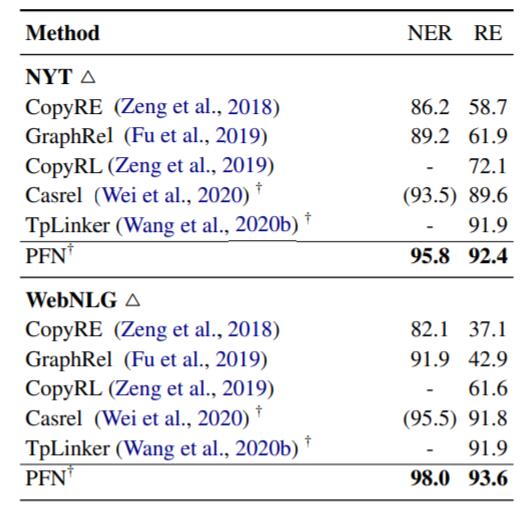
性能超过了之前最强的TPLinker.
在ADE, ACE05, ACE04, SciERC上结果如下:
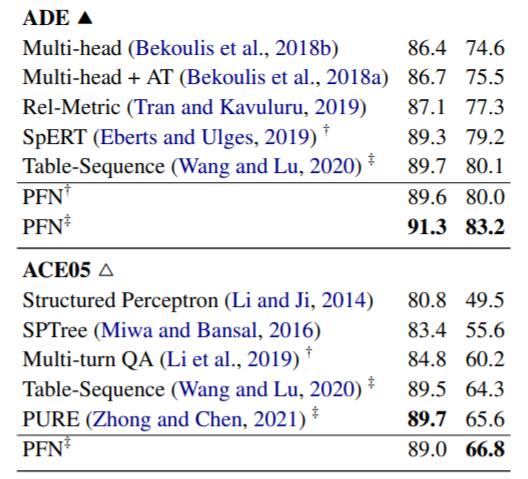
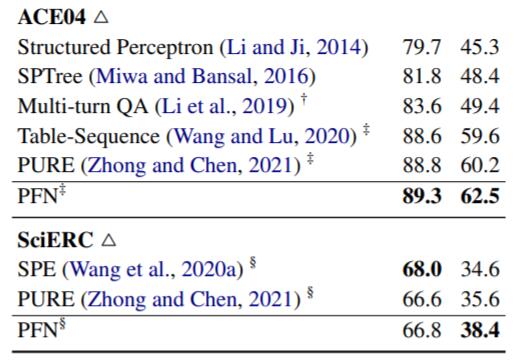
PFN的性能也与强调任务间交互的Table - Sequence和Pipeline设计模型PURE(也是本系列前两篇文章介绍的模型)各有优劣, 整体上来说PFN要好. PURE在ACE05的NER上性能仍为最强.
Ablation Study
在SciERC上消融实验结果如下:
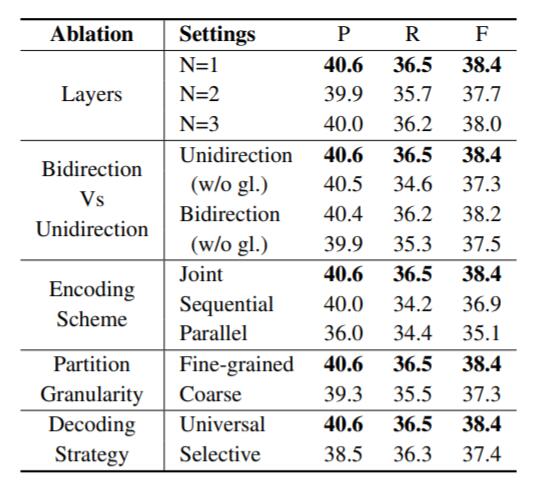
Number of Encoder Layers
堆叠PFN层数不能带来性能提升. 个人认为多层PFN会令信息流混乱, 干扰了任务之间的平衡.
Bidirection Vs Unidirection
无论是单向和还是双向, 使用全局信息都有一点点提升, 但是全局信息对单向增益更大.
Encoding Scheme
作者把PFN Encoder替换成两个LSTM, 观察不同编码方式的效果. Joint代表本文的做法.
在后两种实验中均把PFN Encoder替换成LSTM. Sequential代表Pipeline式的做法, 即单路交互, 先生成实体特征再生成关系特征. Parallel代表两个LSTM都分别编码, 不做交互.
从结果上来看, 平衡交互 > 单路交互 > 不做交互. 似乎平衡交互更有利于召回.
其实有点不公平, 比较单独比较编码策略的时候还是都用LSTM比较好, 可以补一个只用LSTM的Joint结果.
Partition Granularity
作者探究了粗细粒度门控对性能的影响. 例如表示是300维的, 如果把300维劈成10份, 每份都共用30维相同的实体门和关系门, 称为Coarse. 如果300维不劈开, 用300维的实体门和关系门处理, 就称为Fine - grained.
结果表明细粒度更强, 其实也很好解释. 细粒度能更好的区分任务所需要的特征区间.
Decoding Strategy
作者把Pipeline的解码方式称为Selective Decoding, 因为关系模型只对Entity Golden Label解码, 建立在有效实体对之上的. 作者认为, 更好的解码策略是让关系模型把有效和无效实体对都考虑进去, 即Universal Decoding.
Selective是将NER Unit预测得出的有效实体对送给RE Unit解码的结果.
接下来的观点就很有意思了, 作者认为通用解码类似于对比学习, 因为其中包含了无效实体对作为负例, 所以通用解码效果更好.
Effects of Relation Signal on Entity Recognition
在先前的研究中, NER的实体信息对RE有帮助是大家公认的, 但RE是否对NER有益仍然有争议.
Analysis on Entity Prediction of Different Types
因为在主实验结果中, PFN的表现没有很抢眼, 作者认为, 可能是ACE05中包含很多不属于任何三元组的实体.
因此作者将NER任务的结果分为三元组内的实体预测, 三元组外的实体预测, 观察它们的差距:
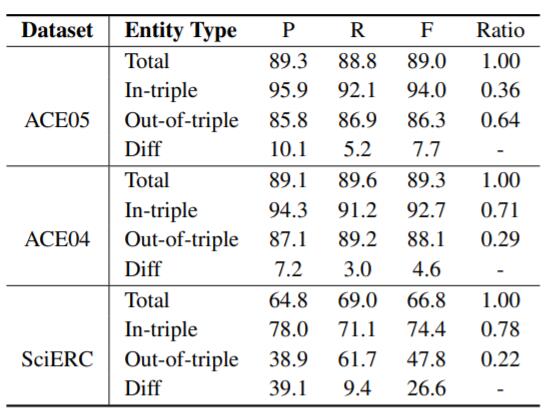
结果发现, 在三元组内的实体预测和在三元组外的实体预测性能有巨大差距, 在不借助关系信息时, 精度下降的很厉害. 与ACE05上NER SOTA Pipeline模型PURE对比, PFN的NER性能似乎与三元组外的实体百分比负相关, 即对于联合模型来说, 三元组外的实体越多, NER性能越差. 因为在三元组内的实体和三元组外的实体预测推理时本质上是不同的, 在三元组内部的实体预测可以借助关系信息, 而三元组外实体预测却不能.
Robustness Test on Named Entity Recognition
在ACE05上的鲁棒性测试结果如下:
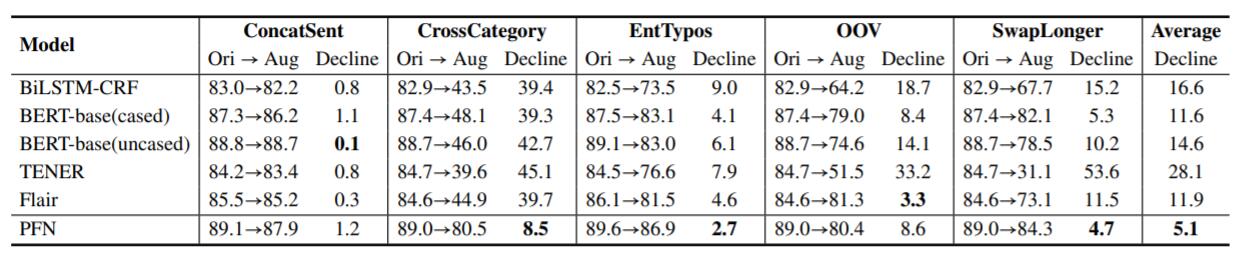
相较于其他模型, PFN的鲁棒性非常好.
Does Relation Signal Helps in Predicting Entities
与PURE中得出的结论相反, 作者认为关系信息对实体预测影响很大.
PURE中的实验是在ACE05上做的, 而忽略了ACE05上的三元组外实体的巨大影响.
附录中还有CasRel, TPLinker, PFN三者在NYT和WebNLG上应对重叠三元组的详细表现, 结果表明PFN在处理重叠三元组的实力也很出色.
Summary
本文从多任务学习视角, 以任务间不平衡的信息交互为出发点, 通过划分, 过滤在最基础的特征区域上控制任务间的信息流通, 再结合整句的全局特征, 用两个任务特化的Task Unit用填表的方法解决联合抽取问题.
我个人认为, 这是一篇挺有想法的文章, 顺着论文的引文, 发现其灵感似乎也来自于ON - LSTM, 感兴趣的可以直接看苏神博客.
PFN进一步的说明了联合抽取中NER和RE任务之间是密不可分的, 并有效驳斥了PURE中的论点.
从论文本身来说, 是很优秀的一篇. 实验完备, 论据充分, 图也很好看.