SDN: Synchronous Dual Network with Cross-Type Attention for Joint Entity and Relation Extraction

本文前置知识:

• LSTM: 循环神经网络小结

Synchronous Dual Network with Cross-Type Attention for Joint Entity and Relation Extraction

本文是论文Synchronous Dual Network with Cross-Type Attention for Joint Entity and Relation Extraction的阅读笔记和个人理解, 论文来自EMNLP 2021.

Basic Idea

联合抽取因NER和RE之间的复杂交互而有挑战性, 现有的方法经把二者通过一个共享的网络来解决, 丢失了实体类型和关系类型的相互依赖.

因此, 作者从多任务学习角度, 设计了一种跨类型注意力的同步对偶网络, 来充分利用实体类型和关系类型之间的联系.

下图是一个实体关系抽取的例子, 需要根据给出的句子来抽取出实体以及其对应的实体类型, 并判断实体之间所存在的关系, 以此组成三元组:

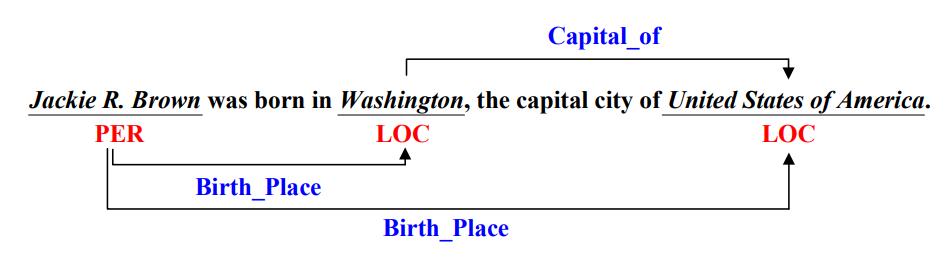
Type - Attention LSTM

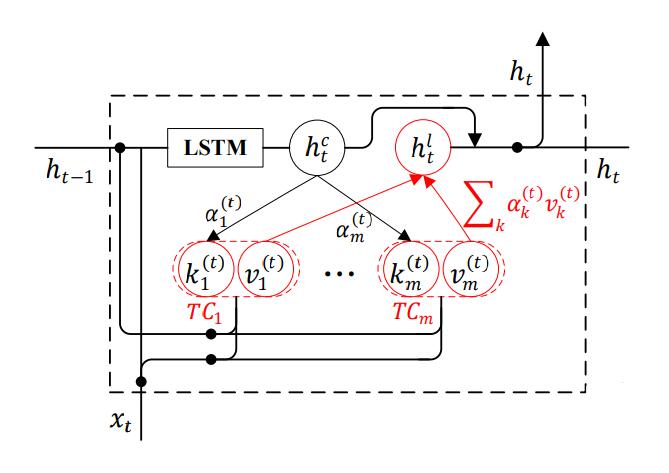
作者设计的框架TA - LSTM(Type Attention LSTM)是基于LSTM的, 作者先介绍了标准LSTM. 在$t$ 时刻, 输入的Token的Embedding为${\mathbf{x}}_t$, 基于细胞状态${\mathbf{c}}_t$ 的隐态输出${\mathbf{h}}_t^c$ 计算流程为:

$$\begin{array}{rl}\left[\begin{array}{c}{\mathbf{i}}_t\\ {\mathbf{o}}_t\\ {\mathbf{f}}_t\\ {\tilde{\mathbf{c}}}_t\end{array}\right]& =\left[\begin{array}{c}\sigma \\ \sigma \\ \sigma \\ \tanh \end{array}\right](\mathbf{W}[{\mathbf{h}}_{t-1};{\mathbf{x}}_t]+\mathbf{b})\\ {\mathbf{c}}_t& ={\mathbf{i}}_t\odot {\tilde{\mathbf{c}}}_t+(\mathbf{1}-{\mathbf{i}}_t)\odot {\mathbf{c}}_{t-1}\\ {\mathbf{h}}_t^c& ={\mathbf{o}}_t\odot \tanh \left({\mathbf{c}}_t\right)\end{array}$$

其中$\mathbf{W},\mathbf{b}$ 为可学习参数, $\sigma$ 为Sigmoid激活函数.

上述式子由上到下分别为: $t$ 时刻的输入门${\mathbf{i}}_t$, 输出门${\mathbf{o}}_t$, 遗忘门${\mathbf{f}}_t$, 初始细胞状态${\tilde{\mathbf{c}}}_t$, 细胞状态${\mathbf{c}}_t$, 隐态输出${\mathbf{h}}_t^c$(也作为上下文表示).

Type - Attention Mechanism

这部分是TA - LSTM额外添加的内容.

在Type - Attention机制中, 对于类型$k$, 以及给定的$t$ 时刻输入${\mathbf{x}}_t$ 和$t-1$ 时刻的隐态${\mathbf{h}}_{t-1}$. 该类型相关的Key - Value对可以由下式计算得来:
$$\left[\begin{array}{l}{\mathbf{k}}_k^{(t)}\\ {\mathbf{v}}_k^{(t)}\end{array}\right]=\left[\begin{array}{c}\sigma \\ \sigma \end{array}\right]({\mathbf{W}}_k[{\mathbf{h}}_{t-1};{\mathbf{x}}_t]+{\mathbf{b}}_k)$$

$k\in [1,\dots ,m]$ 可以是实体类型或关系类型, 其中${\mathbf{W}}_k,{\mathbf{b}}_k$ 为可学习参数, $\sigma$ 为Sigmoid函数. 其实跟${\mathbf{i}}_t,{\mathbf{o}}_t,{\mathbf{f}}_t$ 得来的方式差不多.

这样就可以根据类型数量$m$, 得到$m$ 个类别特化的Key - Value对${\mathbf{K}}^{(t)}=[{\mathbf{k}}_1^{(t)},\dots ,{\mathbf{k}}_m^{(t)}]$ 和${\mathbf{V}}^{(t)}=[{\mathbf{v}}_1^{(t)},\dots ,{\mathbf{v}}_m^{(t)}]$.

接着把上下文表示${\mathbf{h}}_t^c$ 视为Query, 把Attention机制应用到这上面来:
$$\begin{array}{rl}{\mathbf{h}}_t^l& =\mathrm{attention}({\mathbf{h}}_t^c,{\mathbf{K}}^{(t)},{\mathbf{V}}^{(t)})={\mathit{\alpha }}^{(t)}{\mathbf{V}}^{(t)}\\ {\mathit{\alpha }}^{(t)}& =\mathrm{softmax}\left(\frac{{\mathbf{h}}_t^c{\mathbf{K}}^{(t)}{}^{\mathrm{\top }}}{\sqrt{d_e}}\right)\end{array}$$

$\sqrt{d_e}$ 为Hidden state维度.

最后, TA - LSTM的$t$ 时刻上下文表示${\mathbf{h}}_t^c$ 和类别表示${\mathbf{h}}_t^l$ 相加得到$t$ 时刻的最终表示${\mathbf{h}}_t$:

$${\mathbf{h}}_t={\mathbf{h}}_t^c+{\mathbf{h}}_t^l$$

Synchronous Dual Network with Cross - Type Attention

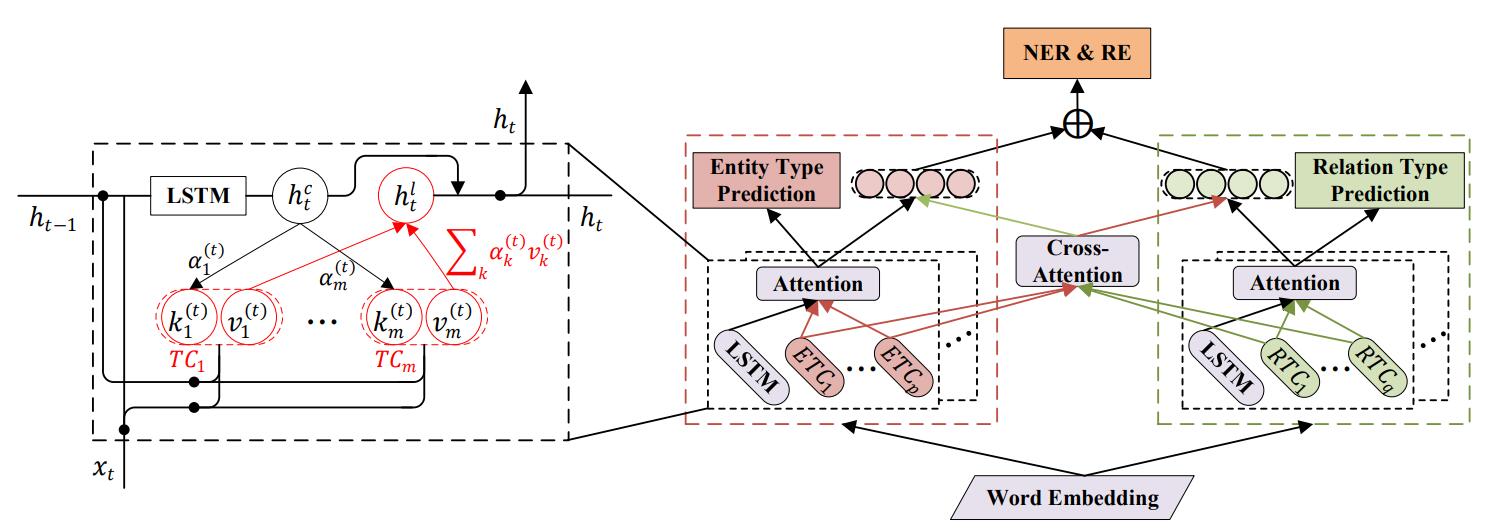
Task Definition

在这里重新给出形式化的实体关系抽取任务定义.

对于给定的包含$n$ 个单词的句子$\mathbf{s}=[w_1,\dots ,w_n]$, RTE的任务目标是抽取出句子$\mathbf{s}$ 中的关系三元组$\mathcal{T}=\{({\mathbf{e}}_i,r,{\mathbf{e}}_j)\mid {\mathbf{e}}_i,{\mathbf{e}}_j\in \mathcal{E},r\in \mathcal{R}\}$. ${\mathbf{e}}_i,{\mathbf{e}}_j,r$ 分别代表关系三元组的Subject, Object, Relation.

Subject, Object规定在实体集$\mathcal{E}={\left\{{\mathbf{e}}_i\right\}}_{i=1}^P$中, 关系从预定义好的关系集$\mathcal{R}=\{{\mathcal{R}}_1,\dots ,{\mathcal{R}}_m\}$中选出, $m$ 为有效关系类型数.

Synchronous Dual Learning

接下来作者将通过Entity Type Learning和Relation Type Learning来捕获实体类型增强的表示${\mathbf{h}}_t^e$, 关系类型增强的表示${\mathbf{h}}_t^r$, 以增强模型对Type的感知力.

Entity Type Learning

NER作为序列标注问题, 实体类型作为标签, 例如PER, LOC, ORG等:

若有$p$ 种实体标签, 每个实体类型都对应一个ETC(Entity Type Cell), 就有$p$ 个ETCs.

为了让模型学会实体类型预测的感知, 所以引入了Entity Type Learning作为辅助任务.

下面的公式有些琐碎, 与原论文保持同步, 但其实并不复杂, 请耐心看完.

从上一节可以仅用LSTM直接得到$t$ 时刻的上下文表示${\mathbf{h}}_t^c$​, 用双向平均来, 即${\overline{\mathbf{h}}}_t^c=\left[(\overrightarrow{{\overline{\mathbf{h}}}_t^c}+\overleftarrow{{\overline{\mathbf{h}}}_t^c})/2\right]$.

并由Type Attention机制得到一组与每种关系一一对应的Key - Value对 ${\overline{\mathbf{K}}}^{(t)}=[{\overline{\mathbf{k}}}_1^{(t)},\dots ,{\overline{\mathbf{k}}}_p^{(t)}]$, ${\overline{\mathbf{V}}}^{(t)}=[{\overline{\mathbf{v}}}_1^{(t)},\dots ,{\overline{\mathbf{v}}}_p^{(t)}]$, 其中的每个实体类型$p$ 对应的Key和Value也是由单向LSTM生成后, 将双向平均而来, 即 ${\overline{\mathbf{k}}}_l^{(t)}=\left[(\overrightarrow{{\overline{\mathbf{k}}}_l^{(t)}}+\overleftarrow{{\overline{\mathbf{k}}}_l^{(t)}})/2\right]$, ${\overline{\mathbf{v}}}_l^{(t)}=\left[(\overrightarrow{{\overline{\mathbf{v}}}_l^{(t)}}+\overleftarrow{{\overline{\mathbf{v}}}_l^{(t)}})/2\right],(l\in [1,\dots ,p])$.

$t$ 时刻实体类型相关的表示由两个方向拼接而成, ${\mathbf{h}}_t^e=[\overrightarrow{{\mathbf{h}}_t^e}\oplus \overleftarrow{{\mathbf{h}}_t^e}]$, 整个序列的实体类型表示记为${\mathbf{H}}^{(e)}=[{\mathbf{h}}_1^e,\dots ,{\mathbf{h}}_n^e]$.

根据上述过程, 每个时间步$t$ 都能得到不同的Type Specific Key - Value对.

然后把上下文表示${\overline{\mathbf{h}}}_t^c$ 和不同实体类型的Key${\overline{\mathbf{k}}}_l^{(c)}$做缩放点积, 得到当前时刻Token最相似的实体类型$T_l^e$:
$$p(T_l^e\mid w_t)=\mathrm{softmax}\left(\frac{{\bar{\mathbf{h}}}_t^c{\bar{\mathbf{k}}}_l^{(t)\mathrm{\top }}}{\sqrt{d_e}}\right)$$

然后用极大似然优化:

$${\mathcal{L}}_{ET}=-\sum _{t=1}^n\log \left(p(T_t^e\mid w_t)\right)$$

Relation Type Learning

同样的, 跟Entity Type Learning相类似, Relation Type Learning也是用来强化模型对类型感知的辅助任务.

因为存在相同实体对存在多种关系的情况(EPO问题), 所以用多标签来标注, 即用0, 1标签来表明实体之间的关系, 例如:

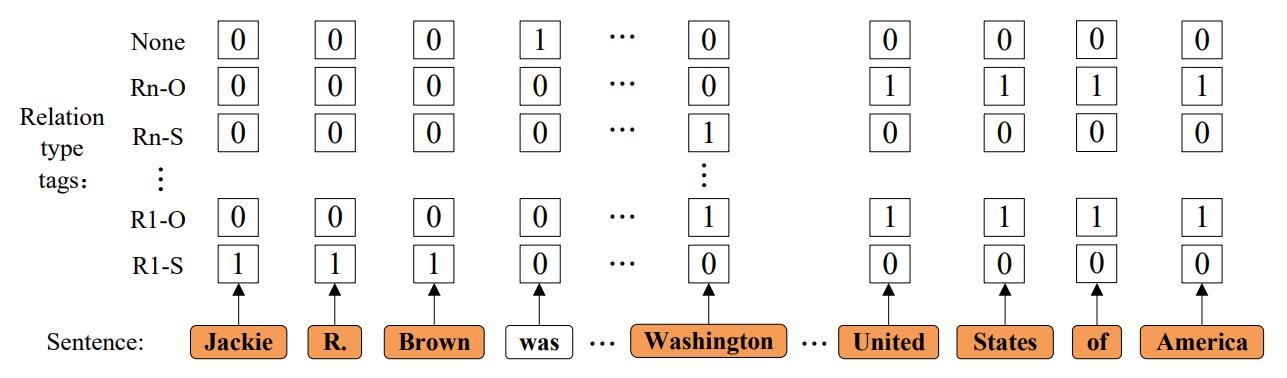
在这里, 作者区分了Subject和Object的位置关系, 并将其纳入标签中. 设$M$ 为关系数量, 加上没有关系的情况, 共含有$2\times M+1$ 种标签.

下内容与Entity Type Learning完全类似, 这里只是将实体类型转换为$q$ 种关系类型, 不再多加赘述.

上下文表示为${\hat{\mathbf{h}}}_t^c=\left[(\overrightarrow{{\hat{\mathbf{h}}}_t^c}+\overleftarrow{{\hat{\mathbf{h}}}_t^c})/2\right]$, Key - Value对 ${\hat{\mathbf{K}}}^{(t)}=[{\hat{\mathbf{k}}}_1^{(t)},\dots ,{\hat{\mathbf{k}}}_q^{(t)}]$, ${\hat{\mathbf{V}}}^{(t)}=[{\hat{\mathbf{v}}}_1^{(t)},\dots ,{\hat{\mathbf{v}}}_q^{(t)}]$, 由双向后求和平均得到, ${\hat{\mathbf{k}}}_l^{(t)}=\left[(\overrightarrow{{\hat{\mathbf{k}}}_l^{(t)}}+\overleftarrow{{\hat{\mathbf{k}}}_l^{(t)}})/2\right]$,$\left[(\overrightarrow{{\hat{\mathbf{v}}}_l^{(t)}}+\overleftarrow{{\hat{\mathbf{v}}}_l^{(t)}})/2\right],(l\in [1,\dots ,q])$

最后也是将双向拼接得到关系表示, ${\mathbf{h}}_t^r=[\overrightarrow{{\mathbf{h}}_t^r}\oplus \overleftarrow{{\mathbf{h}}_t^r}]$, 整个句子的关系表示记为${\mathbf{H}}^{(e)}=[{\mathbf{h}}_1^r,\dots ,{\mathbf{h}}_n^r]$.

因为是多标签问题, 所以用的是Sigmoid得到$w_t$ 的关系类型$T_l^r$:

$$p(T_l^r\mid w_t)=\mathrm{sigmoid}\left(\frac{{\hat{\mathbf{h}}}_t^c{\hat{\mathbf{k}}}_l^{(t)\mathrm{\top }}}{\sqrt{d_e}}\right)$$

也是用极大似然优化:

$${\mathcal{L}}_{RT}=-\sum _{t=1}\sum _{r=1}^2\{\log {\left(p(T_t^r\mid w_t)\right)}^{\mathbb{I}\{{\hat{T}}_t^r=1\}}+\log {(1-p(T_t^r\mid w_t))}^{\mathbb{I}\{{\hat{T}}_t^r=0\}}\}$$

Cross - Type Attention Mechanism

其实在Entity Type Learning和Relation Type Learning中的Entity Type和Relation Type使用是独立的, 所以接下来作者需要让它们彼此产生交互.

对于Entity Type Learning中得到的实体类型增强的表示${\mathbf{h}}_t^e$, 以及关系类型相关的Key - Value对${\hat{\mathbf{K}}}^{(t)},{\hat{\mathbf{V}}}^{(t)}$, 关系 - 实体表示${\mathbf{c}}_t^e$ 可以由前面讲过的Type - Attention机制得到.

与之相似的, 对于Relation Type Learning中得到的关系类型增强表示${\mathbf{h}}_t^r$, 以及实体类型相关的Key - Value对${\overline{\mathbf{K}}}^{(t)},{\overline{\mathbf{V}}}^{(t)}$, 实体 - 关系表示${\mathbf{c}}_t^r$ 也可以由Type - Attention得到. 即:
$$\begin{array}{rl}{\mathbf{c}}_t^e& =\mathrm{attention}({\mathbf{h}}_t^e,{\hat{\mathbf{K}}}^{(t)},{\hat{\mathbf{V}}}^{(t)})\\ {\mathbf{c}}_t^r& =\mathrm{attention}({\mathbf{h}}_t^r,{\overline{\mathbf{K}}}^{(t)},{\overline{\mathbf{V}}}^{(t)})\end{array}$$

注: 该Cross Attention形式绝非首次出现, 在多模态模型ViLBERT 中早就已经有把两种跨模态信息互相作为Query的方法. 只不过这里是将两种模态换为两种包含相关性的任务而已, 这二者十分相似.

然后仿照TA - LSTM unit的最后, 把两种表示相加作为新的实体类型增强表示和新的关系类型增强表示:
$$\begin{array}{rl}{\tilde{\mathbf{h}}}_t^e& ={\mathbf{c}}_t^e+{\mathbf{h}}_t^e\\ {\tilde{\mathbf{h}}}_t^r& ={\mathbf{c}}_t^r+{\mathbf{h}}_t^r\end{array}$$
这也就是处理NER和RE前的最终表示形式了.

Joint Entity and Relation Extraction

下面的内容才是针对实体关系联合抽取的模型设计, 这部分设计的非常简单, 因为本文主要侧重点在于前面.

首先把Entity Type Learning中得到的实体表示${\tilde{\mathbf{h}}}_t^e$ 和Relation Type Learning关系表示${\tilde{\mathbf{h}}}_t^r$ 拼接起来, 得到一个联合表示:

$${\tilde{\mathbf{h}}}_t={\tilde{\mathbf{h}}}_t^e\oplus {\tilde{\mathbf{h}}}_t^r$$

Named Entity Recognition

在NER任务中, 使用BIESO标签, 用Softmax和一层线性层搞定:
$$y_t=\mathrm{softmax}({\mathbf{W}}_e{\tilde{\mathbf{h}}}_t+{\mathbf{b}}_e)$$

用极大似然优化即可:
$${\mathcal{L}}_E=-\sum _{t=1}^n\log \left(y_t\right)$$

Relation Extraction

作者Follow了前人的做法, 因为RE是一个与实体对相关的多标签任务, 所以这里做了实体对穷举, 判断Token $i$ 和Token $j$ 之间的关系$r^{\prime }$:

$$\begin{array}{c}\mathbf{m}=\varphi ({\mathbf{W}}_m({\tilde{\mathbf{h}}}_i\oplus {\tilde{\mathbf{h}}}_j)+{\mathbf{b}}_m)\\ y_{i,j}^{r^{\prime }}=\mathrm{sigmoid}({\mathbf{W}}_{r^{\prime }}\mathbf{m}+{\mathbf{b}}_{r^{\prime }})\end{array}$$

其中${\mathbf{W}}_m,{\mathbf{b}}_m,{\mathbf{W}}_{r^{\prime }},{\mathbf{b}}_{r^{\prime }}$ 为可学习参数, $\varphi$ 为ReLU.

然后用二分类交叉熵做Loss:

$${\mathcal{L}}_R=-\sum _{r^{\prime }=1}^M\sum _{i,j=1}^n\{\log {\left(y_{i,j}^{r^{\prime }}\right)}^{\mathbb{I}\{{\hat{y}}_{i,j}^{r^{\prime }}=1\}}+\log {(1-y_{i,j}^{r^{\prime }})}^{\mathbb{I}\{{\hat{y}}_{i,j}^{\prime }=0\}}\}$$

其中${\hat{y}}_{i,j}^{r\prime }$ 为关系的Golden Label.

至此, SDN的模型结构已经完全确定:

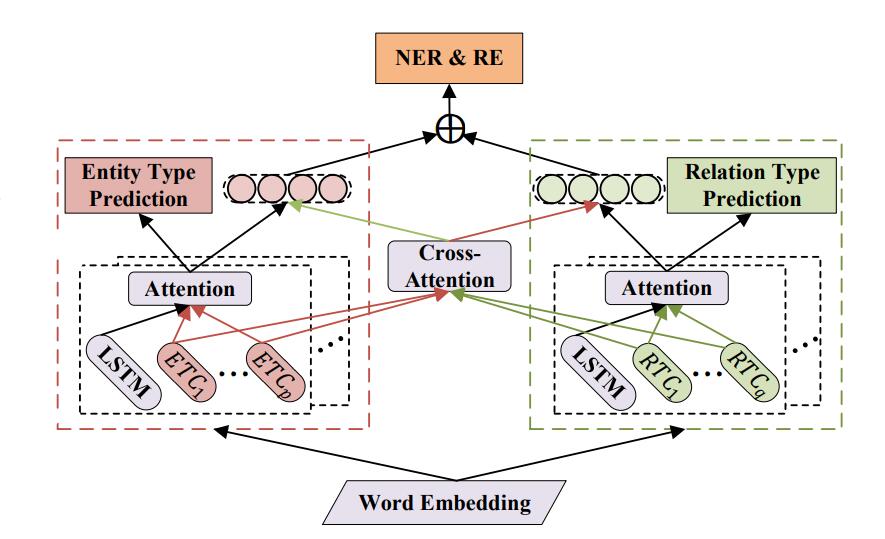
其实就是用TA - LSTM和ETC提供的信息完成辅助任务Entity Type Prediction, 再由这部分信息和Cross Attention组合, 经过简单的变换处理NER. 关系侧则完全同理, 不再叙述.

Training

Training的Loss一共是五个, 最后加上一个L2正则化Loss:

$$\mathcal{L}={\lambda }^{t1}{\mathcal{L}}_{ET}+{\lambda }^{t2}{\mathcal{L}}_{RT}+{\lambda }^e{\mathcal{L}}_E+{\lambda }^r{\mathcal{L}}_R+\frac{\lambda }{2}|\mathrm{\Theta }{|}^2$$

$\lambda$ 为各个任务的权重系数, $\mathrm{\Theta }$ 为模型参数.

Inference

在推断时, 需要判断三元组是否正确.

对于NER抽取出的实体集$\mathcal{E}$ 中的实体, 有Subject ${\mathbf{e}}_i=[w_{{\xi }_i},\dots ,w_{{\zeta }_i}]$, Object $e_j=[w_{{\xi }_j},\dots ,w_{{\zeta }_j}]$, 关系$r$ 下的概率为$p_r$ 为:
$$p_r=\frac{1}{\left|{\mathbf{e}}_i\right|}\frac{1}{\left|{\mathbf{e}}_j\right|}\sum _{f={\xi }_i}^{{\zeta }_i}\sum _{s={\xi }_j}^{{\zeta }_j}{y}_{f,s}^r$$
$\left|{\mathbf{e}}_i\right|,\left|{\mathbf{e}}_j\right|$ 为${\mathbf{e}}_i,{\mathbf{e}}_j$ 的长度, 仅当$p_r>\theta$ 时三元组成立, $\theta$ 为阈值.

这种计算方式确实比较特殊, 是将实体内所有Token对逐一求和平均来确定两实体之间是否存在指定关系.

Experiments

作者使用了RTE上最常用的两个Benchmark NYT和WebNLG, 统计信息如下:

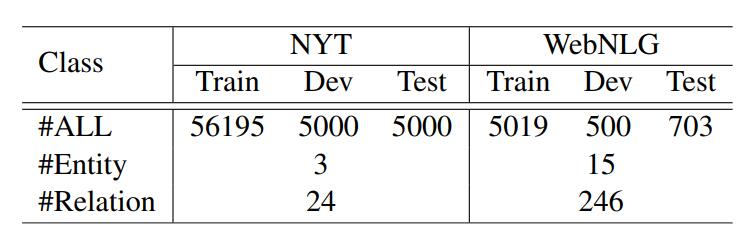
Main Results

作者将SDN分别与多任务类, Tagging类, 生成类放在一起对比, 结果如下(应该指的是精确匹配结果):

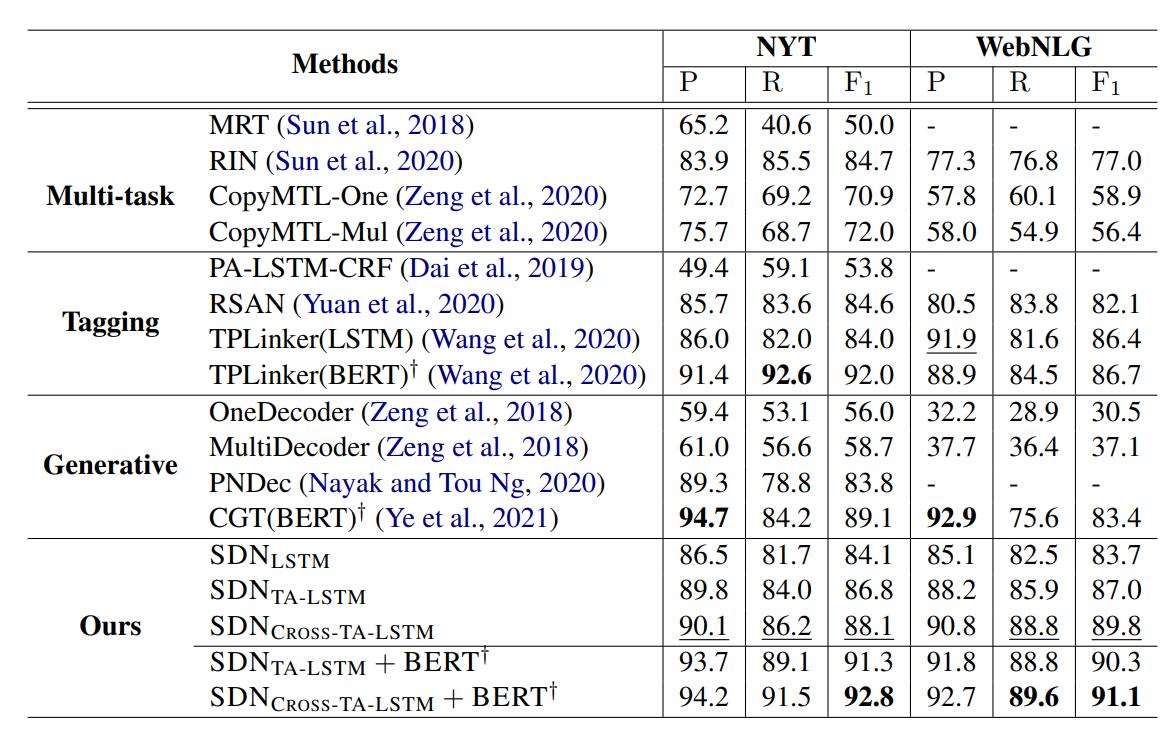
SDN在F1上是最好的.

Ablation Experiments

文中消融实验如下:

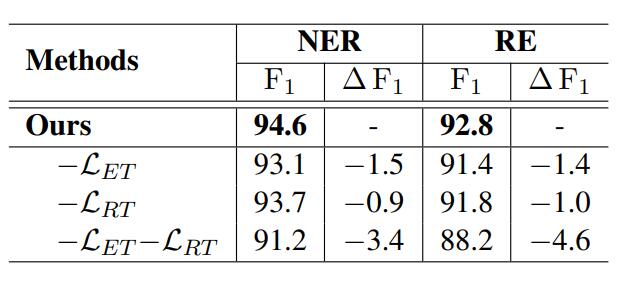
Entity Type Learning和Relation Type Learning对模型性能均有相当大提升, 而且是对NER和RE任务都有影响, 并且能观察到NER和RE任务之间的关联性很强.

Analysis of Inference Threshold

作者做了不同阈值$\theta$ 和模型结果之间变化图:

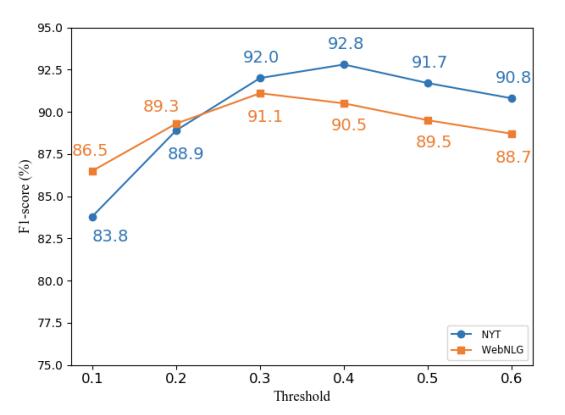
作者将阈值对性能的影响归因与WebNLG和NYT之间实体长度不一.

Case Study

作者做了Case Study, 如下:

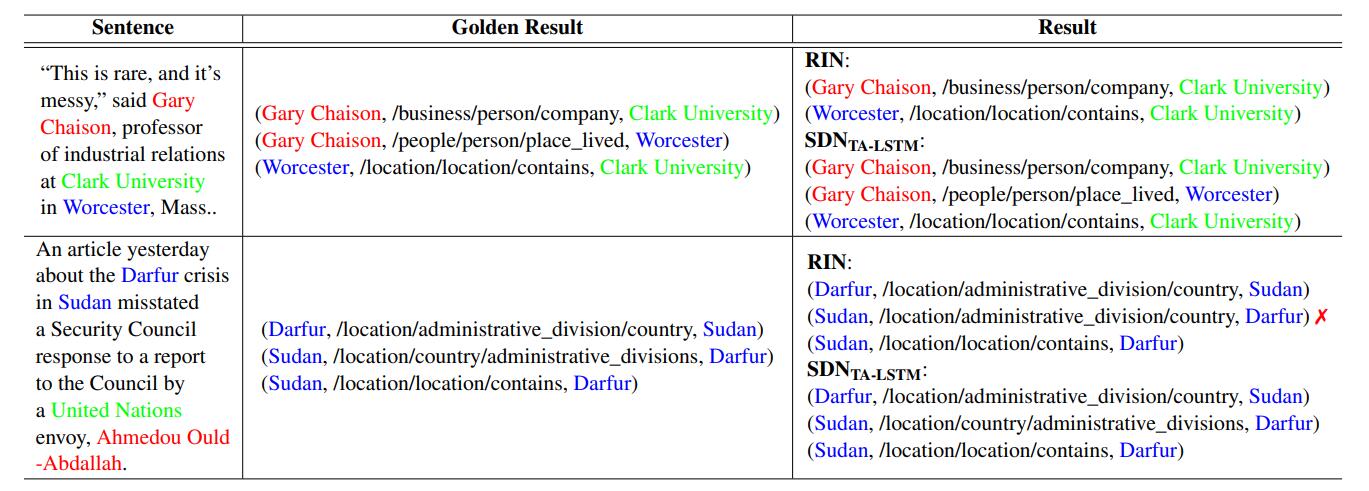
Summary

作者从实体类型和关系类型的假设入手, 提出了一种基于TA - LSTM和Cross Type Attention的同步对偶网络, 通过强调对实体类型的感知, 关系类型的感知, 以及跨类型注意力解决了实体关系抽取问题.

但其实从文章中看出, 能把这个想法做Work是一件非常不容易的事情, 引入了额外的两个辅助任务, 除去正则外4个Loss属实难顶. 文章中的符号描述比较混乱, 尤其是两个辅助任务那部分, 但其实不复杂,