2020.09.07: 重写了LSTM和GRU的描述.
2020.08.22: 对部分内容进行了更新.
循环神经网络 Recurrent Neural Network
面对时序型数据, 如自然语言, 乐谱, 金融数据等包含隐含的时间信息在内的数据, 不能采用原始的稠密神经网络, 会产生很多问题. 比如, 很容易就产生海量的参数, 或者输入输出的神经元很有可能是不确定的, 最主要的是无法将时序的信息传递给稠密神经网络. 采用循环神经网络可以很好的处理时序问题.
RNN的基本结构
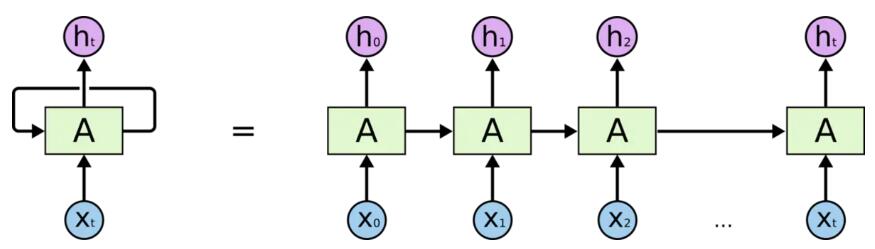
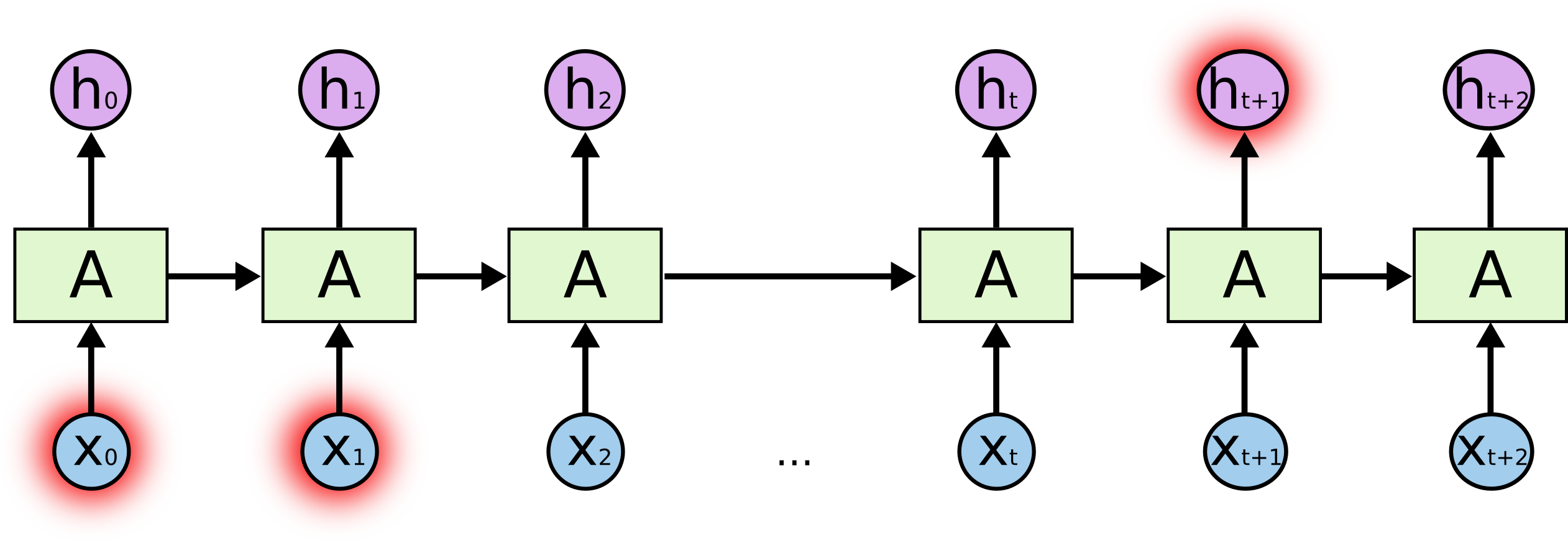
RNN因为满足循环递归的结构, 很多时候也画成左边折叠的样子. 能够看到, 下方的$X_i$ 对应着$t$时刻的输入. 在图中没有画出来的是, 对于图中的$A$ 实际上是一个含有若干个神经元的与输入输出相连的神经网络(其实对应数学结构就是一个矩阵), 只不过隐藏层之间相互有了连接, 下面这个图可能更好解释一些:
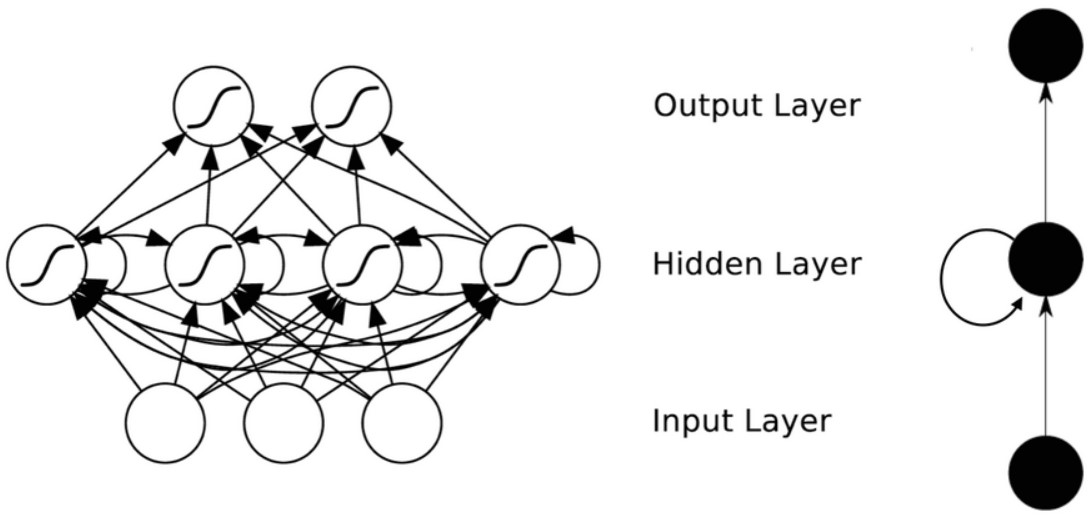
在新的时刻$t$ ,输入视为是$t-1$时刻的神经元结果和$t$时刻的时序序列输入$X_t$的合成结果. 假设激活函数$f$, 当前时刻为$t$有:
$$
\displaylines{
A_t = f(UX_t + WA_{t-1} + b_a) \\
h_t = f(VA_t + b_y)}
$$
在进行计算时, 既然是循环使用的神经元, 那么在时刻尺度上它的参数一定是共享的, 即对于同一组RNN, 它们的$U, W, V, b$ 采用的都是相同的值, 这也符合我们对递归的理解, RNN每个时间步都在做相同的事情, 只是输入不同. 并且在实际计算的过程中, 经常将$U$和$W$合并为同一个矩阵, 将$X_t, A_{t-1}$也合并成一个矩阵做矩阵乘.
其实上述过程就是RNN的前向传播, 非常的符合逻辑, 也同时隐含了它只能进行串行计算的弊病. 其实反向传播只要把前向传播过程反过来就行了, 损失函数为所有时刻的损失平均值.
RNN的几种结构
RNN也可以分为很多种, 有一对一, 一对多, 多对一, 多对多, 具体采用哪种需要结合具体的任务目标而定.
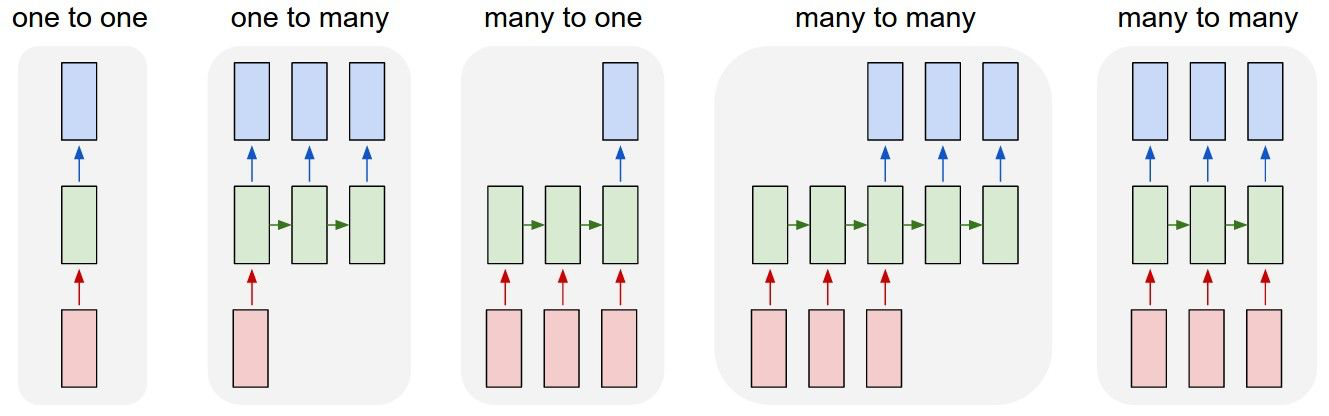
经典RNN由于结构输入和输出必须是一一对应的,应用范围受限很大. 图中所示的第一种多对多经常用于机器翻译, 前一段没有输出的神经网络对应的称为encoder即编码器, 后一段有输出的神经网络称为decoder即解码器, 机器在经过编码器读完整个句子后从解码器获取输出. 第二种多对多经常用于多对多经常用于序列生成.
RNN的采样
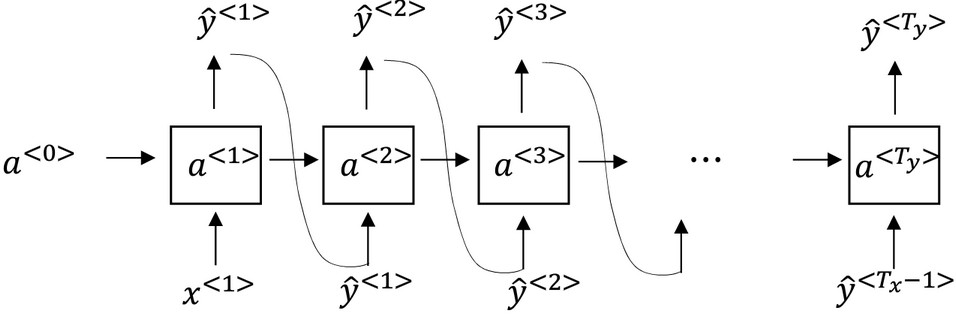
假设有个已经训练好的模型, 那么我们对输入$x^{<1>}$和$a^{<0>}$都置为零向量, 然后让RNN自己预测第一个单词的概率向量$\hat y^{<1>}$, 根据这个概率利用例如np.random.choice获取一个单词的index, 将这个单词的one-hot形式作为下时刻的输入. 当然不一定是单词级别的RNN, 字符级别也可以用, 但是计算成本非常大, 一般只有很多专业词汇才用.
RNN的梯度爆炸和梯度消失
RNN因为是循环的结构, 循环多次很容易导致网络层数加深, 这样前面的网络参数很难被反向传播影响. 比如说RNN可能很难记住一个长句子里的时态语态信息, 其每个时刻的输出主要由临近的几个时刻所影响, 导致不善于处理长期依赖问题. 必须引入一些结构来传递需要被长期记忆的信息.
长短期记忆神经网络LSTM Long Short-Term Memory
LSTM于1997年在Long Short-Term Memory中出现, 是一种尝试保存长期记忆避免梯度消失的RNN. LSTM主要有四个部分, 遗忘门, 输入门, 输出门, 细胞状态. 因为引入了循环神经网络的记忆机制, 常形象地将结构单位称为记忆细胞(memory cell).
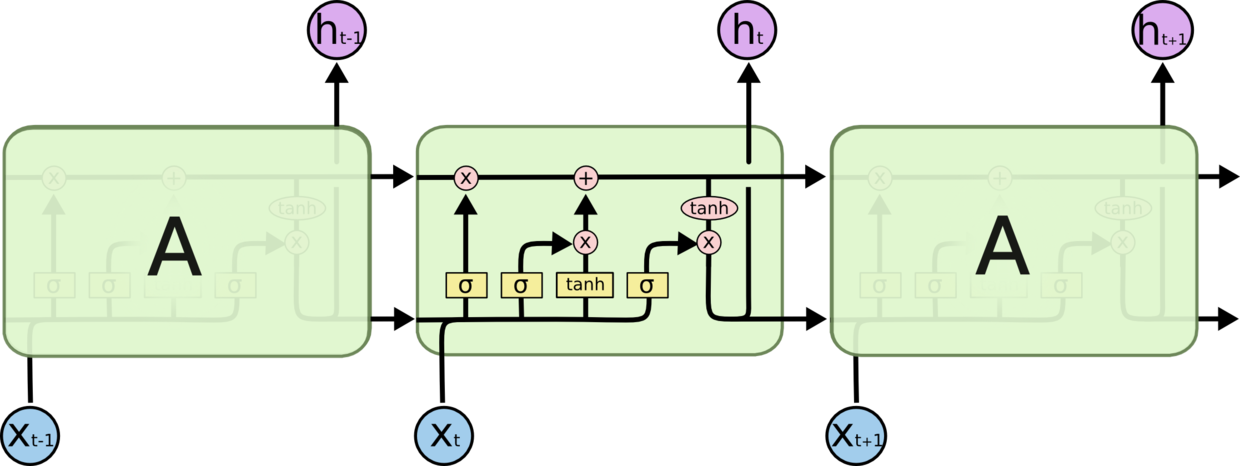
LSTM中所有的向量操作如下:

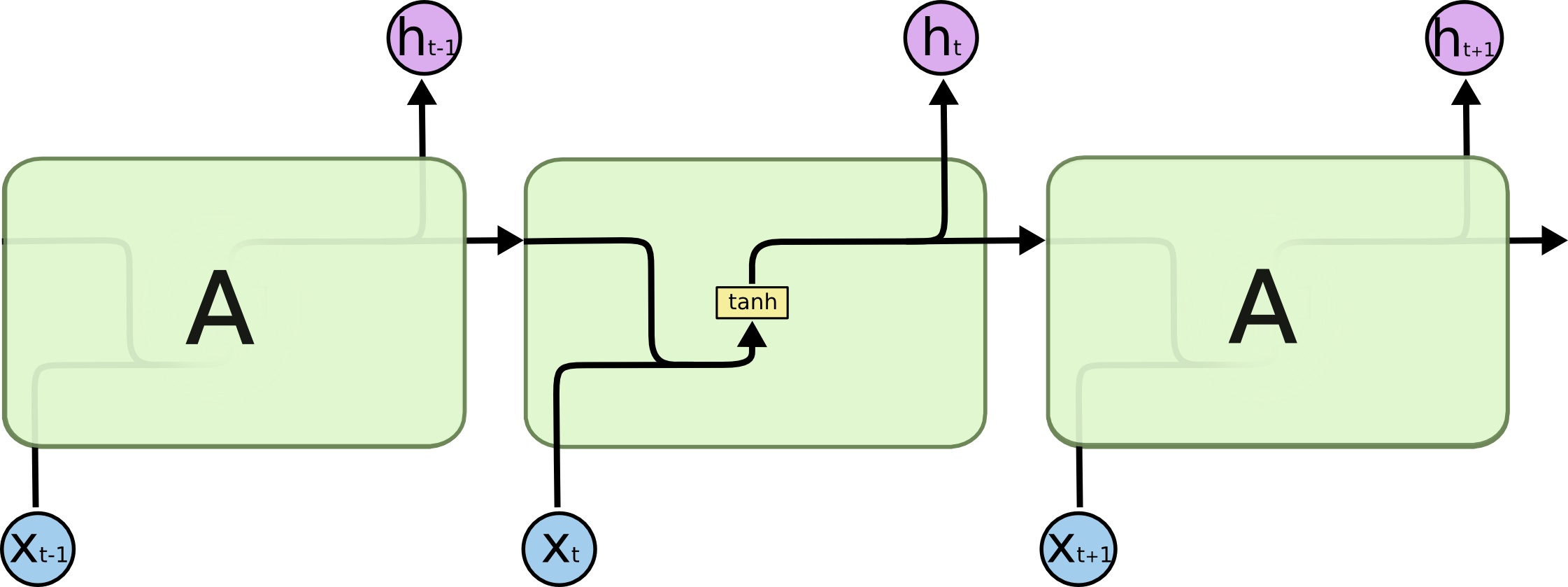
黄框框代表神经层(注意是一层神经层, 不单单是图中标注的激活函数), 粉圈圈代表某种向量的操作, 单箭头代表向量的流向, 汇聚箭头代表向量的concat, 分离箭头代表向量拷贝成了两份.
LSTM最上面的那条水平线代表细胞状态, 细胞存储的状态实际上就是需要长期记忆的信息. 这条路上只有遗忘门和输入门能够对细胞状态进行更改, 只有一些少量的线性交互, 实际上这条线是非常容易不发生任何转变而传递到下一个时刻的. 如下所示:
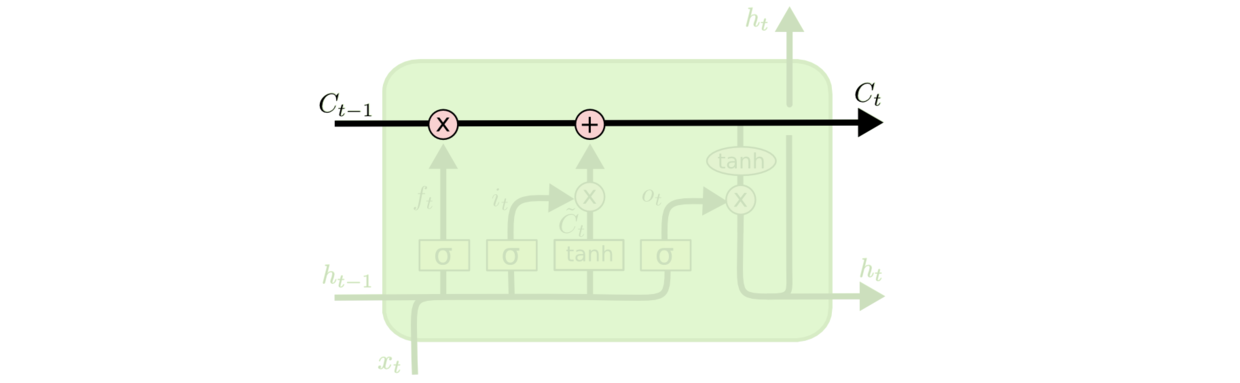
下面来看数据在LSTM中从输入到输出的完整过程.
数据输入后, 数据首先经过LSTM的遗忘门. 遗忘门接收了当前时刻$t$的输入$x_t$和上个时刻的隐藏状态 $h_{t-1}$, 经过$\sigma$函数的处理, 能够决定到底留下多少在细胞状态中. $f_t=1$表示完全记住这个信息, $f_t=0$代表完全忘记这个值. 基于上文预测下文词的语言模型中, 可能细胞状态会包含前文的主题, 那么最好记住$h_{t-1}$, 如果得到一个新的语言主题, 则希望遗忘掉过去的信息.
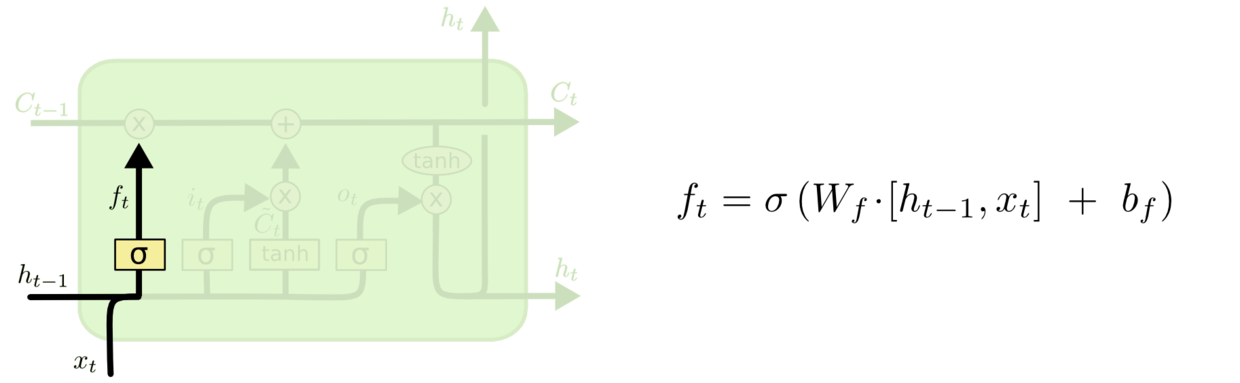
第二步决定在细胞状态中储存什么样的信息, 与之对应的结构称为输入门. 输入门有两条并行的向量流向. 左侧线路用$\sigma$函数决定有哪些位置上的信息是需要更新的, 右侧线路利用$tanh$为等待细胞状态更新时的使用的候选值创建一个新的向量.
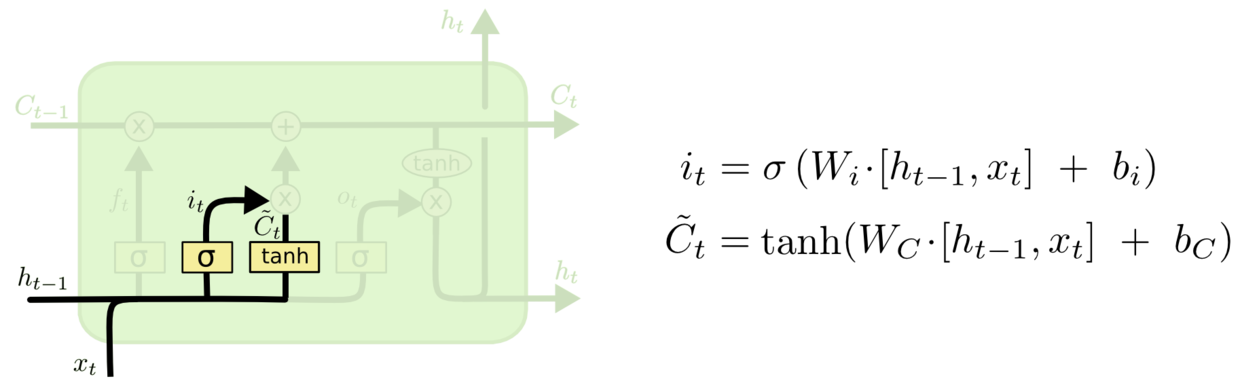
第三步便是对细胞状态更新的过程. 细胞状态先通过遗忘门所给出的遗忘程度对先前状态遗忘, 然后再将输入门的左右两条并行路线的结果计算出来, 与细胞状态相加, 就完成了细胞状态的更新. 从下述式子中可以看到, 对于旧信息的遗忘和新信息的输入, 是让它们自己决定到底留下哪些, 加入哪些. 这点与GRU的风格是不同的, 后面会提到.

最后决定要输出的东西, 所对应的结构就是输出门. 输出基于细胞当前的状态, 但会经过一次过滤才输出. 与输入门对应, 先利用$\sigma$函数得到一个输出的系数, 再将细胞状态过一次$tanh$将信息压到$[-1, 1]$之间, 与系数相乘就得到了结果. 也正是因为输出门的设置, 导致LSTM的输出$h_t$ 其实只是经过输出门过滤后的$C_t$ 的一部分信息.
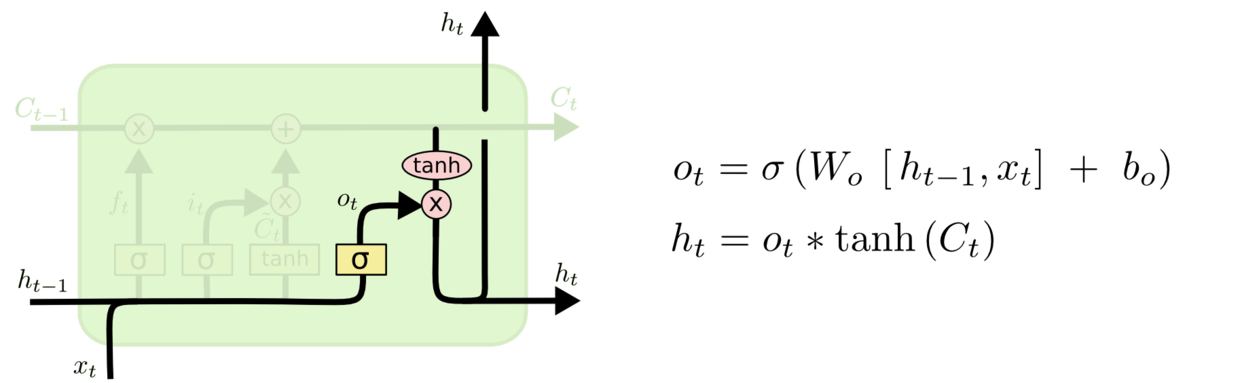
LSTM的遗忘门和输入门都对细胞状态进行了更改, 先遗忘再存储. 输出门发生作用的时候是不会对细胞状态再次更改的.
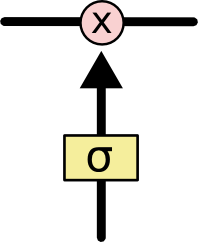
在这三种门控结构中, 不难观察门控作为一种关键的结构, 能起到让信息选择性通过的作用, 根据$\sigma$函数的特性, 向量的每个维度都能够得到一个介于$[0, 1]$ 之间的值, 在与其他向量相乘时, 可以作为保留或遗忘程度的依据.
门控循环单元 GRU Gate Recurrent Unit
GRU是一个LSTM的一个变种, 于Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation中提出. 它比LSTM参数更少, 结构更简单, 具有更高的效率, 达到的精度和LSTM相近. GRU和LSTM同样借鉴了门控的思想, 在RNN中添加不同的门控, 从而决定是否要更新信息. GRU结构比较简单, 所以用一张图就完全可以说得清.
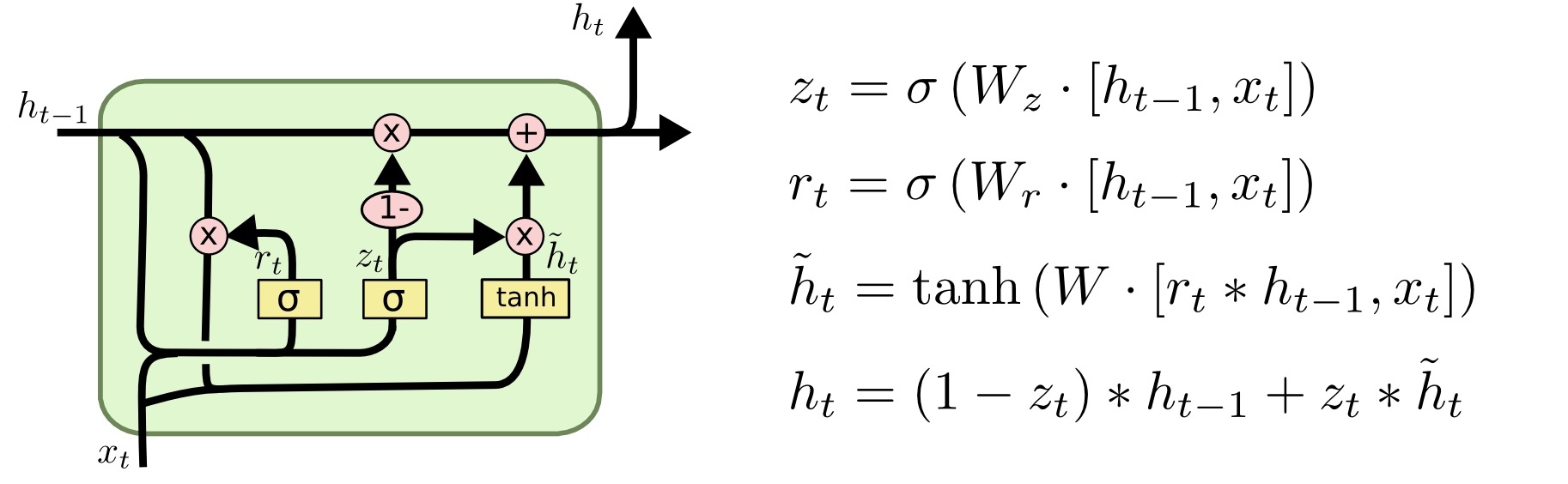
GRU分别有两个门控结构, 分别是重置门$r_t$ (reset gate)和更新门$z_t$ (update gate).
重置门: 重置门用于决定丢弃先前信息的程度.
更新门: 更新门能决定在当前时刻要丢弃哪些信息和要添加哪些新信息. 作用类似于LSTM中的遗忘门和输入门.
$\tilde h_t$表示的是相较于普通RNN的隐藏状态输出$h_t$的候选, 最终不会使用它, 仅作为最终输出$h_t$的依据.
下面描述一下数据在GRU的传播过程:
对于重置门, 上一个时刻$t-1$的隐藏状态$h_{t-1}$和当前时刻的输入$x_t$传入GRU, 通过重置门后将得到一个将$h_{t-1}$和$x_t$ 丢弃的程度系数向量$r_t$.
而对于更新门, 同样将是上一个时刻$t-1$的隐藏状态$h_{t-1}$和当前时刻的输入$x_t$传入, 获得表示一个更新程度的系数向量$z_t$.
重置门和更新门(或者说重置系数和更新系数)的值已经求出来了, 接着利用重置门的丢弃系数和上一时刻的隐藏状态$h_{t-1}$ 相乘, 并结合当前时刻输入, 经过激活函数为$tanh$ 的神经层, 求出当前时刻的候选隐藏状态$\tilde {h_t}$.
根据重置和更新的互斥关系, 求出当前时刻隐藏状态$h_t$ . 当更新门$z_t$的值趋近于1时, 就更倾向于更新记忆细胞的信息, $h_t$的值会和$\tilde{h_{t}}$相仿, 反之不更新, 即仍然沿用上个时刻的信息$h_{t-1}$.
两个门的作用在进行运算中十分明显, 重置门决定了要丢弃多少先前信息, 直接影响了$\tilde{h_t}$, 间接影响了结果$h_t$, 更新门决定了细胞要替换多少新信息, 直接影响最终输出的隐藏状态 $h_t$.
LSTM与GRU对比及个人理解
首先要明确细胞状态和隐藏状态的区别, 细胞状态$C_t$ 代表的是初始时刻一直到$t$ 时刻的全局信息, 而$h_t$ 代表的是初始时刻到$t-1$ 时刻的全局信息影响下, 当前$t$ 时刻的上下文表示.
LSTM中, 有细胞状态这个概念, GRU只有隐藏状态. LSTM对信息的保留更加细腻, 但对下一个时刻只暴露部分信息, 因为在LSTM中$h_t$ 才是真正的输出, $C_t$ 只作为一个信息载体继续传递下去. 相比于LSTM, GRU则更加简单粗暴, 对下个时刻暴露全部信息.
LSTM对细胞状态的更新过程中, 经过遗忘门和输入门后求出细胞状态$C_t$ 是相互独立的, 即$f_t$ 和 $i_t$ 之间没有关联, 由遗忘门和输入门分别控制遗忘和存储. 而对于GRU来说, 既然$h_t$ 被包含在$C_t$ 中了, 干脆将细胞状态与隐藏状态合并, 在求出最终隐藏状态$h_t$ 时, 而去除了细胞状态后, 当前信息与全局信息是此消彼长的, 即对于写入新信息和保留旧信息是互相制约的, 故令$f_t$ 和 $i_t$ 的总和1, 直接用一个更新门$z_t$ 来代替原有的遗忘门和输入门. 同样因为输出的调整, 重置门本质上是输出门的一种变化.
双向RNN和RNN的堆叠
双向RNN解决了网络不知道下文信息的问题, 使网络不光会结合前文进行判断, 还会结合后文信息进行预测. 如下图所示, 对于给定的$x^{<1>}, x^{<2>}, x^{<3>}, x^{<4>}$, 每个时刻都增加一个反向链接的神经元. 这样RNN就构成了一个无环图. 当进行前向传播时, 信息会从左到右, 再从右逆着传回来, 最后再做出预测, 即对于$t$时刻的预测值$y_t$, 是由$a^{<t\rightarrow>}$和$a^{<t\leftarrow>}$, $x^{<t>}$共同决定的.
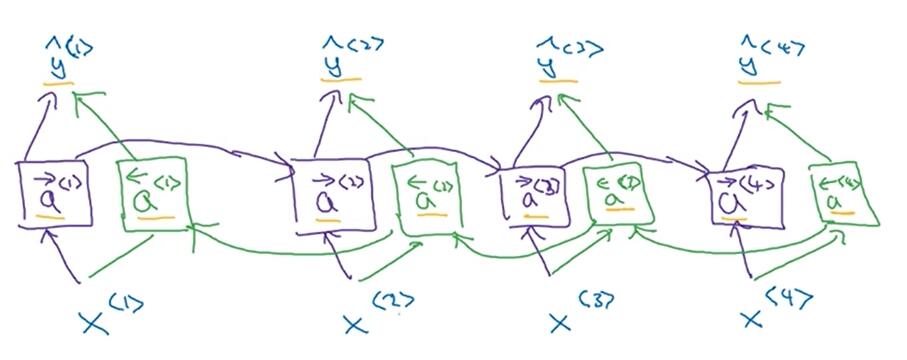
和下面这张图是一样的:
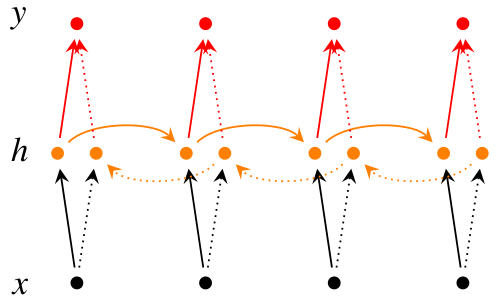
RNN的堆叠方式其实也非常简单, 就是按照层数往上传递隐藏状态, 最终得到预测值.
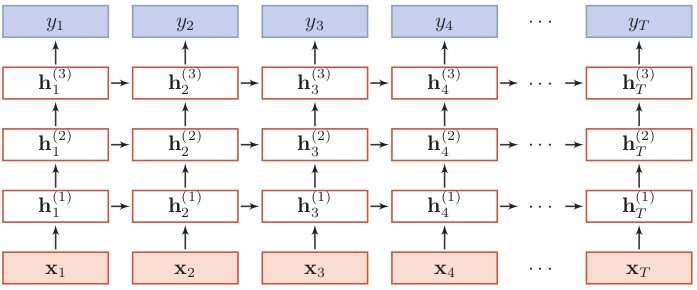
如果是若干双向RNN, 堆叠起来也和普通RNN大同小异:


