本文前置知识:
Denoising Diffusion Implicit Models
- 论文: Denoising Diffusion Implicit Models, ICLR 2021.
在DDPM. 中我们提到, 其Forward Process和Generative(Reverse) Process都是在一阶马尔科夫链下定义的, 如下图左:

但是依赖马尔科夫链的DDPM生成速度非常慢, 有没有什么办法来加速采样, 实现更高效率的生成呢? 要是能在这个基础上和DDPM的Forward Process兼容, 只改变Generative Process, 以此达到复用训练好的DDPM模型权重的目的就更好了.
Background
先来简单的回顾一下DDPM., 并且需要注意DDIM中的定义与DDPM中存在一些差异.
对于数据分布$q(\boldsymbol{x}_0)$, 生成类模型希望用可学习的分布$p_\theta(\boldsymbol{x}_0)$ 来近似$q(\boldsymbol{x}_0)$. DDPM将其建模为一个联合概率分布:
$$
p_\theta\left(\boldsymbol{x}_0\right)=\int p_\theta\left(\boldsymbol{x}_{0: T}\right) \mathrm{d} \boldsymbol{x}_{1: T}, \quad \text { where } \quad p_\theta\left(\boldsymbol{x}_{0: T}\right):=p_\theta\left(\boldsymbol{x}_T\right) \prod_{t=1}^T p_\theta^{(t)}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)
$$
其中$\boldsymbol{x}_1, \dots, \boldsymbol{x}_T$ 为隐变量.
DDPM中将Forward Process $q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)$ 定义为一个高斯过程的马尔科夫链:
$$
q\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right):=\prod_{t=1}^T q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}\right), \text { where } q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}\right):=\mathcal{N}\left(\sqrt{\frac{\alpha_t}{\alpha_{t-1}}} \boldsymbol{x}_{t-1},\left(1-\frac{\alpha_t}{\alpha_{t-1}}\right) \boldsymbol{I}\right)
$$
DDIM中的$\alpha_t$ 对应的是DDPM论文中的$\bar\alpha_t$.
其中, $\alpha_{1:T} \in (0, 1]^T$ 为逐渐减小的序列. 此时的$\boldsymbol{x}_t$ 具有一阶马尔科夫性, 即其分布受到$\boldsymbol{x}_{t-1}$ 影响.
与Forward Process相对应的Reverse Process就为 $q(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t)$, 需要用模型$p_\theta(\boldsymbol{x}_{0:T})$ 来近似, $p_\theta(\boldsymbol{x}_{0:T})$ 倒推的过程称为Generative Process.
如果你看过DDPM的论文, 这里的叫法可能会有些迷惑.
DDPM中将Generative Process $p_\theta\left(\boldsymbol{x}_{0: T}\right)$ 称为Reverse Process.
DDIM中更明确, 将Generative Process $p_\theta\left(\boldsymbol{x}_{0: T}\right)$ 和Reverse Process $q(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t)$ 区分开, $q$ 指的是推理分布.
根据一阶马尔科夫性, 发现$q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)$ 可以直接得到:
$$
q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right):=\int q\left(\boldsymbol{x}_{1: t} \mid \boldsymbol{x}_0\right) \mathrm{d} \boldsymbol{x}_{1:(t-1)}=\mathcal{N}\left(\boldsymbol{x}_t ; \sqrt{\alpha_t} \boldsymbol{x}_0,\left(1-\alpha_t\right) \boldsymbol{I}\right)
$$
因此可以用$\boldsymbol{x}_0$ 和噪声$\epsilon$ 的线性组合来表示$\boldsymbol{x}_t$:
$$
\boldsymbol{x}_t=\sqrt{\alpha_t} \boldsymbol{x}_0+\sqrt{1-\alpha_t} \epsilon, \quad \text { where } \quad \epsilon \sim \mathcal{N}(\mathbf{0}, \boldsymbol{I})
$$
$\alpha_T$ 接近于0, 且对于所有的$\boldsymbol{x}_0$, 都能使$q(\boldsymbol{x}_T \mid \boldsymbol{x}_0)$ 收敛于标准正态分布.
DDPM中用如下目标函数优化去噪网络参数$\theta$:
$$
L_\gamma\left(\epsilon_\theta\right):=\sum_{t=1}^T \gamma_t \mathbb{E}_{\boldsymbol{x}_0 \sim q\left(\boldsymbol{x}_0\right), \epsilon_t \sim \mathcal{N}(\mathbf{0}, \boldsymbol{I})}\left[\Vert\epsilon_\theta^{(t)}\left(\sqrt{\alpha_t} \boldsymbol{x}_0+\sqrt{1-\alpha_t} \epsilon_t\right)-\epsilon_t\Vert_2^2\right]
$$
其中, $\epsilon_\theta := \set{\epsilon_\theta^{(t)}}^{T}_{t=1}$ 为$T$ 个函数的集合, $\gamma:=[\gamma_1, \dots, \gamma_T]$ 为取决于$\alpha_{1:T}$ 的正系数.
Variational Inference for Non-Markovian Forward Processes
通过对DDPM的Training Object $L_\gamma$ 的观察, 发现$L_\gamma$ 实际上只取决于边缘分布$q(\boldsymbol{x}_{t}\mid\boldsymbol{x}_0)$, 而不是取决于联合分布$q(\boldsymbol{x}_{1:T} \mid \boldsymbol{x}_0)$. 因此可以考虑将$q(\boldsymbol{x}_{t}\mid\boldsymbol{x}_0)$ 推导过程中的遵循马尔科夫假设的$q(\boldsymbol{x}_{t}\mid\boldsymbol{x}_{t-1})$ 剥离, 建立一个非马尔科夫Forward Process, 从而得到一个新的Reverse Process与Generative Process.
因此这个观察也给我们一个启发, 只要任何满足DDPM条件, 且能保证模型具有等价目标函数的Forward Process设计都是可行的.
Non-Markovian Forward Processes
如果不再考虑马尔科夫性, 可以将Forward Process $q_\sigma\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)$ 重写为一组由方差$\sigma$ 为索引的一系列分布:
$$
\begin{equation}
q_\sigma\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right):=q_\sigma\left(\boldsymbol{x}_T \mid \boldsymbol{x}_0\right) \prod_{t=2}^T q_\sigma\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)
\end{equation}
$$
由于DDPM的定义, 所以需要满足$t > 1$ 时, $q_\sigma (\boldsymbol{x}_T\mid\boldsymbol{x}_0)=\mathcal{N}\left(\sqrt{\alpha_T}\boldsymbol{x}_0, (1-\alpha_T)\boldsymbol{I}\right)$, 即$q_\sigma\left(\boldsymbol{x}_T\mid\boldsymbol{x}_0\right)$ 已知.
回忆一下DDPM, 在DDPM中出现的$q_\sigma\left(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_t, \boldsymbol{x}_0\right)$ 实际上被我们用一阶马尔科夫链替换成$q_\sigma\left(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_t\right)$. 若想摆脱对马尔科夫链的依赖, 这里肯定就不能再把它替换成$q_\sigma\left(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_t\right)$ 了, 需要直接定义分布$q_\sigma\left(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_t, \boldsymbol{x}_0\right)$:
$$
\begin{equation}
q_\sigma\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)=\mathcal{N}\left(\sqrt{\alpha_{t-1}} \boldsymbol{x}_0+\sqrt{1-\alpha_{t-1}-\sigma_t^2} \cdot \frac{\boldsymbol{x}_t-\sqrt{\alpha_t} \boldsymbol{x}_0}{\sqrt{1-\alpha_t}}, \sigma_t^2 \boldsymbol{I}\right)
\end{equation}
$$
当然, $q_\sigma\left(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_t, \boldsymbol{x}_0\right)$ 肯定不能乱定义. 它不能违背老祖宗(DDPM)的规矩, 必须得保证对于任意的时间步$t$, 都满足$q_\sigma\left(\boldsymbol{x}_t\mid\boldsymbol{x}_0\right)=\mathcal{N}\left(\sqrt{\alpha_t} \boldsymbol{x}_0, (1 - \alpha_t\right)\boldsymbol{I})$. 这样可以保证DDIM的Forward Process和DDPM的Forward Process兼容.
有了$q_\sigma\left(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_t, \boldsymbol{x}_0\right)$, Forward Process就可以进一步的用贝叶斯法则得到:
$$
q_\sigma\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}, \boldsymbol{x}_0\right)=\frac{q_\sigma\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right) q_\sigma\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)}{q_\sigma\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_0\right)}
$$
它仍然是一个高斯分布. 但是与DDPM的Forward Process不同, 这里的Forward Process不再是一个马尔科夫链, 因为每个$\boldsymbol{x}_t$ 不光依赖于$\boldsymbol{x}_{t-1}$, 还依赖于$\boldsymbol{x}_0$.
$\sigma$ 决定了Forward Process的随机程度. 当$\sigma \rightarrow \boldsymbol{0}$ 时, 有一极端情况, 即已知$\boldsymbol{x}_0, \boldsymbol{x}_{t}$ 时, 所有的$\boldsymbol{x}_{t-1}$ 都是确定的.
Proof
分布$q_\sigma\left(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_t, \boldsymbol{x}_0\right)$ 的形式是怎么得到的呢?
这部分是证明, 从正反两个方向, 不感兴趣的可以跳过, 不过还是推荐看下.
Reverse Proof
逆向证明仅需证明作者构造的$q_\sigma\left(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_t, \boldsymbol{x}_0\right)$ 能使得DDPM的Forward Procees的设计$q_\sigma\left(\boldsymbol{x}_t\mid\boldsymbol{x}_0\right)=\mathcal{N}\left(\sqrt{\alpha_t} \boldsymbol{x}_0, (1 - \alpha_t\right)\boldsymbol{I})$ 对于所有的时间$t \leq T$ 都能被满足.
显然只需要检验中间过程是否有$q_\sigma\left(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_0\right)=\mathcal{N}\left(\sqrt{\alpha_{t-1}} \boldsymbol{x}_0, (1 - \alpha_{t-1}\right)\boldsymbol{I})$.
根据边缘分布, 用$\boldsymbol{x}_{t}$ 的积分计算$q_\sigma\left(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_0\right)$:
$$
q_\sigma\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_0\right):=\int_{\boldsymbol{x}_t} q_\sigma\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right) q_\sigma\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right) \mathrm{d} \boldsymbol{x}_t
$$
这个积分是二者的卷积运算, 而且$q_\sigma\left(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_0\right)$ 是一个高斯分布, 设其为$\mathcal{N}(\mu_{t-1}, \Sigma_{t-1})$, 将条件$q_\sigma\left(\boldsymbol{x}_t\mid\boldsymbol{x}_0\right)=\mathcal{N}\left(\sqrt{\alpha_t} \boldsymbol{x}_0, (1 - \alpha_t\right)\boldsymbol{I})$ 代入$q_\sigma\left(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_t, \boldsymbol{x}_0\right)$, 可得:
$$
\begin{aligned}
\mu_{t-1} &= \sqrt{\alpha_{t-1}} \boldsymbol{x}_0+\sqrt{1-\alpha_{t-1}-\sigma_t^2} \cdot \frac{\sqrt{\alpha_t} \boldsymbol{x}_0-\sqrt{\alpha_t} \boldsymbol{x}_0}{\sqrt{1-\alpha_t}} \\\
&= \sqrt{\alpha_{t-1}}\boldsymbol{x}_0 \\
\Sigma_{t-1} &= \sigma_t^2\boldsymbol{I} + \frac{1-\alpha_{t-1}-\sigma_t^2}{1-\alpha_t}(1-\alpha_t)\boldsymbol{I} \\\
&=(1-\alpha_{t-1})\boldsymbol{I}
\end{aligned}
$$
方差$\Sigma_{t-1}$ 的求解用到了方差分解公式.
所以有$q_\sigma\left(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_0\right)=\mathcal{N}\left(\sqrt{\alpha_{t-1}} \boldsymbol{x}_0, (1 - \alpha_{t-1}\right)\boldsymbol{I})$. 因此按照递推, 对于所有的$t \leq T$, 都能够满足$q_\sigma\left(\boldsymbol{x}_t\mid\boldsymbol{x}_0\right)=\mathcal{N}\left(\sqrt{\alpha_t} \boldsymbol{x}_0, (1 - \alpha_t\right)\boldsymbol{I})$.
Forward Proof
当然, 一个更合理的视角是用待定系数法正着推, 思路来自生成扩散模型漫谈(四):DDIM = 高观点DDPM - 科学空间|Scientific Spaces.
在DDPM中可知, $q_\sigma\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)$ 本身就是一个正态分布, 因此我们可以更一般的假设$q_\sigma\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right) \sim \mathcal{N}(k\boldsymbol{x}_0 + m\boldsymbol{x}_{t}, \sigma^2)$, 便有:
$$
\boldsymbol{x}_{t-1} = k\boldsymbol{x}_0 + m\boldsymbol{x}_t + \sigma\epsilon, \quad \text { where } \quad \epsilon \sim \mathcal{N}(\mathbf{0}, \boldsymbol{I})
$$
在DDPM中我们的假设是:
$$
\boldsymbol{x}_t=\sqrt{\alpha_t} \boldsymbol{x}_0+\sqrt{1-\alpha_t} \epsilon^\prime, \quad \text { where } \quad \epsilon^\prime \sim \mathcal{N}(\mathbf{0}, \boldsymbol{I})
$$
$\boldsymbol{x}_{t-1}$ 中有$\boldsymbol{x}_t$, 将$\boldsymbol{x}_t$ 代入$\boldsymbol{x}_{t-1}$, 得:
$$
\begin{aligned}
\boldsymbol{x}_{t-1} &= k\boldsymbol{x}_0 + m\boldsymbol{x}_t + \sigma\epsilon \\
&=k\boldsymbol{x}_0 + m(\sqrt{\alpha_t} \boldsymbol{x}_0+\sqrt{1-\alpha_t} \epsilon^\prime) + \sigma\epsilon \\
&=(k+m\sqrt{\alpha_{t}}) \boldsymbol{x}_0 + m\sqrt{1-\alpha_t}\epsilon^\prime + \sigma\epsilon
\end{aligned}
$$
此处的$\epsilon, \epsilon^\prime$ 互相独立, 来自于两个不同的分布, 两个正态分布的和的方差为二者方差之和.
由于$\boldsymbol{x}_{t-1}=\sqrt{\alpha_{t-1}} \boldsymbol{x}_0+\sqrt{1-\alpha_{t-1}} \epsilon$, 所以由待定系数法有:
$$
\begin{aligned}
k+m\sqrt{\alpha}&=\sqrt{\alpha_{t-1}} \\
m^2(1-\alpha_t) + \sigma^2 &= 1-\alpha_{t-1}
\end{aligned}
$$
可求得:
$$
\begin{aligned}
m &= \sqrt{\frac{1-\alpha_{t-1}-\sigma^2}{1-\alpha_t}} \\
k &= \sqrt{\alpha_{t-1}} - \sqrt{\alpha_t} \cdot \sqrt{\frac{1-\alpha_{t-1}-\sigma^2}{1-\alpha_t}}
\end{aligned}
$$
这样将$m, k$ 代回到$\boldsymbol{x}_{t-1}$ 中, 就得到了$q_\sigma\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)$, 得证.
Generative Process
接下来定义Generative Process $p_\theta(\boldsymbol{x}_{0:T})$, 这个过程中的每一步$p_\theta^{(t)}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)$ 都需要使用刚才定义的$q_\sigma\left(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_t, \boldsymbol{x}_0\right)$. 从直觉上来说, 对于一个Noisy Observation $\boldsymbol{x}_t$, 首先需要对$t$ 时刻的$\boldsymbol{x}_0$ 预测, 然后使用$q_\sigma\left(\boldsymbol{x}_{t-1}\mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)$ 来得到$\boldsymbol{x}_{t-1}$.
DDPM Forward Process中的条件为$\boldsymbol{x}_0 \sim q(\boldsymbol{x}_0)$, $\epsilon \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$, $\boldsymbol{x}_t=\sqrt{\alpha_t} \boldsymbol{x}_0 + \sqrt{1- \alpha_t} \epsilon$. 在Generative Process中, 想要使用$q_\sigma\left(\boldsymbol{x}_{t-1}\mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)$, 肯定不能依赖于推理时的最终目标$\boldsymbol{x}_0$ 对吧, 进而需要在已知$\boldsymbol{x}_t$ 的情况下用$f_\theta^{(t)}$ 将$\boldsymbol{x}_0$ 估计出来.
将 $\boldsymbol{x}_t=\sqrt{\alpha_t} \boldsymbol{x}_0 + \sqrt{1- \alpha_t} \epsilon$ 变形, 得到$\boldsymbol{x}_0 = \left(\boldsymbol{x}_t - \sqrt{1 - \alpha_{t}} \cdot \epsilon \right) / \sqrt{\alpha_t}$, 其中的$\epsilon$ 可以由模型$\epsilon^{(t)}_\theta(\boldsymbol{x}_t)$ 预测得到. 因此在$\boldsymbol{x}_t$ 处对$\boldsymbol{x}_0$ 的估计 $f_\theta^{(t)}\left(\boldsymbol{x}_t\right)$ 可以写成:
$$
\begin{equation}
f_\theta^{(t)}\left(\boldsymbol{x}_t\right):=\left(\boldsymbol{x}_t-\sqrt{1-\alpha_t} \cdot \epsilon_\theta^{(t)}\left(\boldsymbol{x}_t\right)\right) / \sqrt{\alpha_t}
\end{equation}
$$
接着就可以定义Generative Process $p_\theta(\boldsymbol{x}_{0:T})$, 同时将$q_\sigma\left(\boldsymbol{x}_{t-1}\mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)$ 中的 $\boldsymbol{x}_0$ 替换为$f_\theta^{(t)}\left(\boldsymbol{x}_t\right)$:
$$
\begin{aligned}
p_\theta^{(t)}\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)&= \begin{cases}\mathcal{N}\left(f_\theta^{(1)}\left(\boldsymbol{x}_1\right), \sigma_1^2 \boldsymbol{I}\right) & \text { if } t=1 \\\ \\
q_\sigma\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, f_\theta^{(t)}\left(\boldsymbol{x}_t\right)\right) & \text { otherwise }\end{cases} \\\ \\
p_\theta(\boldsymbol{x}_T)&=\mathcal{N}(\boldsymbol{0}, \boldsymbol{I}) \\\
\end{aligned}
$$
Sampling from Generalized Generative Processes
前面说过, DDPM中的训练目标$L_1$ 只取决于$q(\boldsymbol{x}_{t}\mid\boldsymbol{x}_0)$. 由于上面定义的$q_\sigma\left(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_t, \boldsymbol{x}_0\right)$ 满足$q_\sigma\left(\boldsymbol{x}_t\mid\boldsymbol{x}_0\right)=\mathcal{N}\left(\sqrt{\alpha_t} \boldsymbol{x}_0, (1 - \alpha_t\right)\boldsymbol{I})$ 的假设, 所以DDPM和DDIM的$q_\sigma(\boldsymbol{x}_{t}\mid\boldsymbol{x}_0)$ 是相同的, 因此DDPM和DDIM的目标函数就是等价的(偷个懒这里不证了, 感兴趣的去Reference里找资料看).
所以, 实际上在DDPM用$L_1$ 作为目标函数的同时, 不光训练了基于马尔科夫链的Forward Process对应的Generative Process, 还顺手训练了我们引入$\sigma$ 参数化的非马尔科夫的Forward Process对应的Generative Process. 如此以来就不用重新训DDPM, 这么一看DDPM真是个大善人.
Denoising Diffusion Implicit Models
写出Generative Process $p_\theta(\boldsymbol{x}_{1:T})$ 中基于非马尔科夫推导的$q_\sigma\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, f_\theta^{(t)}\left(\boldsymbol{x}_t\right)\right)$, 得到通过$\boldsymbol{x}_t$ 得到$\boldsymbol{x}_{t-1}$ 的最终表达式:
$$
\boldsymbol{x}_{t-1}=\sqrt{\alpha_{t-1}} \underbrace{\left(\frac{\boldsymbol{x}_t-\sqrt{1-\alpha_t} \epsilon_\theta^{(t)}\left(\boldsymbol{x}_t\right)}{\sqrt{\alpha_t}}\right)}_{\text {“predicted } \boldsymbol{x}_0 \text { “ }}+\underbrace{\sqrt{1-\alpha_{t-1}-\sigma_t^2} \cdot \epsilon_\theta^{(t)}\left(\boldsymbol{x}_t\right)}_{\text {“direction pointing to } \boldsymbol{x}_t \text { “ }}+\underbrace{\sigma_t \epsilon_t}_{\text {random noise }}
$$
其中定义$\alpha_0 := 1$, $\epsilon_t \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$ 为与$\boldsymbol{x}_t$ 无关的标准正态分布噪声. 不同的$\sigma$ 可以决定不同的Generative Process. $\epsilon_\theta$ 是由DDPM训练时候得到的, 所以在推理时采样可以不用对模型重新训练, 调整$\sigma$ 即可.
这个式子由三项组成, 逐一观察:
- 前面一项: 就是$f_\theta^{(t)}\left(\boldsymbol{x}_t\right)$ 前面乘了个$\sqrt{\alpha_{t-1}}$, 整体作用是对$\boldsymbol{x}_0$ 的一个估计值(Predicted $\boldsymbol{x}_0$). 明显的, 在Generative Process的起始阶段($t$ 较大时), 由于$\boldsymbol{x}_{t}$ 相距$\boldsymbol{x}_0$ 还比较远, $\boldsymbol{x}_t$ 已经被大量噪声污染, 在$t$ 时刻预测的$\boldsymbol{x}_0$ 很有可能不太准, 所以这个过程需要多次迭代来实现对$\boldsymbol{x}_0$ 相对准确的估计.
- 中间一项: $\epsilon_\theta^{(t)}$ 是在$t$ 时刻模型预测出的噪声. 对于$\boldsymbol{x}_{t-1}$ 来说, $\boldsymbol{x}_t$ 是对$\boldsymbol{x}_{t-1}$ 添加噪声得到的, 所以这一项指示了$\boldsymbol{x}_t$ 的方向(Direction Pointing to $\boldsymbol{x}_t$). 上面提到过, 对$\hat{\boldsymbol{x}}_{0}$ 的估计并不够准确, 因此这一项可以看成是在$\hat{\boldsymbol{x}}_{0}$ 的基础上引入对$\boldsymbol{x}_{t}$ 方向的修正, 使得Generative Process满足对Forward Process中$\boldsymbol{x}_{t-1} \rightarrow \boldsymbol{x}_t$ 条件的保证, 防止得到的$\boldsymbol{x}_{t-1}$ 偏离$\boldsymbol{x}_{t-1} \rightarrow \boldsymbol{x}_t$ 的路径. 其中的$\sqrt{1 - \alpha_{t-1} -\sigma_t^2}$ 是对$\epsilon_\theta^{(t)}$ 的修正系数. $\epsilon_\theta^{(t)}$ 与$\sigma_t$ 负相关.
- 最后一项: 为了保证$\boldsymbol{x}_{t-1}$ 为概率分布而做的重采样, 即在$t$ 时刻添加的随机噪声$\sigma_t \epsilon_t$. 它是与$\sigma_t$ 正相关的, 总的噪声$\epsilon_\theta^{(t)} + \epsilon_t$ 恰好可以在后两项得到平衡.
当然, $\sigma_t$ 是可以任意选取的, 有两种特殊情况:
- 当有$\sigma_t = \sqrt{(1-\alpha_{t-1}) / (1-\alpha_t)} \sqrt{1-\alpha_t / \alpha_{t-1}}$ 时, Forward Process是马尔科夫链, Generative Process恰好是DDPM..
- 当有$\sigma_t=0$ 时, 在给定$\boldsymbol{x}_{t-1}, \boldsymbol{x}_{0}$ 情况下, 除去$t=1$ 外, Forward Process会变成一个完全确定性的过程, 随机噪声$\epsilon_t$ 也就为0了. 第二项的修正系数恰好为$\sqrt{1-\alpha_{t-1}}$, 有$\boldsymbol{x}_{t-1} = \sqrt{\alpha_{t-1}}f_\theta^{(t)}\left(\boldsymbol{x}_t\right) + \sqrt{1-\alpha_{t-1}}\epsilon^{(t)}_\theta(\boldsymbol{x}_t)$.
虽然$\sigma_t$ 可以任意取, 但对于DDIM, 一般指$\sigma_t=0$ 的情况, 生成的结果不再具有随机性. 所以说它是一种具有DDPM训练目标的隐式概率模型, 因而被称为DDIM(Denoising Diffusion Implicit Model).
Accelerated Generation Processes
正上文所述, DDPM的Training Object $L_1$ 与Forward Process的形式无关, 当$q_\sigma\left(\boldsymbol{x}_t\mid\boldsymbol{x}_0\right)$ 固定时就是确定的. 所以只要满足$q_\sigma\left(\boldsymbol{x}_t\mid\boldsymbol{x}_0\right)=\mathcal{N}\left(\sqrt{\alpha_t} \boldsymbol{x}_0, (1 - \alpha_t\right)\boldsymbol{I})$ 即可, 怎么取Forward Process都没问题.
分析一下, DDIM的两个优势:
- 有了定义在非马尔科夫链上的$q_\sigma\left(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_t, \boldsymbol{x}_0\right)$, 这就使得$\boldsymbol{x}_{t-1}$ 可以依赖对$\boldsymbol{x}_0$ 的估计, 而不单取决于$\boldsymbol{x}_{t}$. 不过注意, 在DDPM中, $t-1, t$ 都来自于连续的时间序列$t \in [1, \dots, T]$, 所以$t-1, t$ 都是连续的. 但在DDIM中由于非马尔科夫性, 这里的$t-1, t$ 不再是一个连续序列中的两个时间步. 觉得别扭可以将它们换个字母, 比如在一个新的不连续子序列$s \in [1, \dots, s_{i-1}, s_{i}, \dots, T]$ 中, $s_{i-1}$ 可以对应DDPM里的$t=900$, $s_i$ 可以对应$t=800$.
- $\sigma_t=0$ 的确定性采样带来了一条确定性轨迹, 消除了随机性, 这个性质使我们在已知$\boldsymbol{x}_t$ 的情况下可以估计到更远的地方, 并具有更高的准确性, 即允许我们跳过更多的步骤采样.
综上, 甚至可以考虑定义长度远小于$T$ 的Forward Process来加速采样过程.
例如, 可以考虑定义在一个$\boldsymbol{x}_{1:T}$ 的子集$\set{\boldsymbol{x}_{\tau_1}, \dots, \boldsymbol{x}_{\tau_S}}$ 上的Forward Process, $\tau$ 为长度为$S$ 的递增子序列$[1, \dots, T]=[\tau_1, \dots, \tau_S]$. 该Forward Process需要满足:
$$
q\left(\boldsymbol{x}_{\tau_i}\mid\boldsymbol{x}_0\right)=\mathcal{N}\left(\sqrt{\alpha_{\tau_i}} \boldsymbol{x}_0, (1 - \alpha_{\tau_i}\right)\boldsymbol{I})
$$
相对应的, 此时的Generative Process是定义在这个子序列$\tau$ 的逆序列$\text{reversed}(\tau)$ 上的采样过程. 此时的Generative Process中$\boldsymbol{x}_{\tau_{i-1}}$ 为:
$$
\boldsymbol{x}_{\tau_{i-1}}=\sqrt{\alpha_{\tau_{i-1}}}\left(\frac{\boldsymbol{x}_{\tau_i}-\sqrt{1-\alpha_{\tau_i}} \epsilon_\theta^{\left(\tau_i\right)}\left(\boldsymbol{x}_{\tau_i}\right)}{\sqrt{\alpha_{\tau_i}}}\right)+\sqrt{1-\alpha_{\tau_{i-1}}-\sigma_{\tau_i}^2} \cdot \epsilon_\theta^{\left(\tau_i\right)}\left(\boldsymbol{x}_{\tau_i}\right)+\sigma_{\tau_i} \epsilon
$$
由于子序列长度$S$ 远远小于原序列长度$T$, 所以推理速度可以实现显著提升, 即”跳步采样“. 例如$\tau=[1, 3]$ 时有:
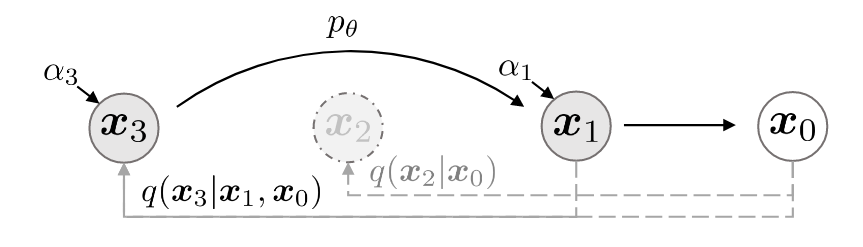
Proof
这里直接抄的论文.
由于$L_1$ 与Forward Process的形式无关, 所以在加速过程中, 可将Forward Process分解为:
$$
q_{\sigma, \tau}\left(\boldsymbol{x}_{1: T} \mid \boldsymbol{x}_0\right)=q_{\sigma, \tau}\left(\boldsymbol{x}_{\tau_S} \mid \boldsymbol{x}_0\right) \prod_{i=1}^S q_{\sigma, \tau}\left(\boldsymbol{x}_{\tau_{i-1}} \mid \boldsymbol{x}_{\tau_i}, \boldsymbol{x}_0\right) \prod_{t \in \bar{\tau}} q_{\sigma, \tau}\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)
$$
其中$\tau$ 为长度为$S$ 的子序列$[1, \dots, T]$, 且$\tau_S =T$, 同时令$\bar{\tau} := \set{1, \dots, T} \backslash \tau$ 为$\tau$ 的补集. 第一项与第二项来自子序列$\tau$, 第三项来自于补集$\bar{\tau}$.
接着, 仿照在推导非马尔科夫的Forward Process, 给出定义:
$$
\begin{gathered}
q_{\sigma, \tau}\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)=\mathcal{N}\left(\sqrt{\alpha_t} \boldsymbol{x}_0,\left(1-\alpha_t\right) \boldsymbol{I}\right) \quad \forall t \in \bar{\tau} \cup\{T\} \\
q_{\sigma, \tau}\left(\boldsymbol{x}_{\tau_{i-1}} \mid \boldsymbol{x}_{\tau_i}, \boldsymbol{x}_0\right)=\mathcal{N}\left(\sqrt{\alpha_{\tau_{i-1}}} \boldsymbol{x}_0+\sqrt{1-\alpha_{\tau_{i-1}}-\sigma_{\tau_i}^2} \cdot \frac{\boldsymbol{x}_{\tau_i}-\sqrt{\alpha_{\tau_i}} \boldsymbol{x}_0}{\sqrt{1-\alpha_{\tau_i}}}, \sigma_{\tau_i}^2 \boldsymbol{I}\right) \quad\forall i \in[S]
\end{gathered}
$$
使得子序列$\tau$ 对应的Forward Process满足条件:
$$
q\left(\boldsymbol{x}_{\tau_i}\mid\boldsymbol{x}_0\right)=\mathcal{N}\left(\sqrt{\alpha_{\tau_i}} \boldsymbol{x}_0, (1 - \alpha_{\tau_i}\right)\boldsymbol{I}) \quad\forall i \in[S]
$$
则对应的Generative Process定义为:
$$
p_\theta\left(\boldsymbol{x}_{0: T}\right):=\underbrace{p_\theta\left(\boldsymbol{x}_T\right) \prod_{i=1}^S p_\theta^{\left(\tau_i\right)}\left(\boldsymbol{x}_{\tau_{i-1}} \mid \boldsymbol{x}_{\tau_i}\right)}_{\text {use to produce samples }} \times \underbrace{\prod_{t \in \bar{\tau}} p_\theta^{(t)}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_t\right)}_{\text {in variational objective }}
$$
发现仅部分模型用于生成样本. 条件分布为:
$$
\begin{gathered}
p_\theta^{\left(\tau_i\right)}\left(\boldsymbol{x}_{\tau_{i-1}} \mid \boldsymbol{x}_{\tau_i}\right)=q_{\sigma, \tau}\left(\boldsymbol{x}_{\tau_{i-1}} \mid \boldsymbol{x}_{\tau_i}, f_\theta^{\left(\tau_i\right)}\left(\boldsymbol{x}_{\tau_{i-1}}\right)\right) \quad \text { if } i \in[S], i>1 \\
p_\theta^{(t)}\left(\boldsymbol{x}_0 \mid \boldsymbol{x}_t\right)=\mathcal{N}\left(f_\theta^{(t)}\left(\boldsymbol{x}_t\right), \sigma_t^2 \boldsymbol{I}\right) \quad \text { otherwise }
\end{gathered}
$$
因此采用子序列$\tau$ 进行Generative Process来得到$\boldsymbol{x}_0$ 是可行的.
Relevance to Neural ODEs
在$\sigma_t=0$ 时, DDIM的生成是确定性的, 可以将DDIM重写为一个Neural ODE:
$$
\begin{equation}
\frac{\boldsymbol{x}_{t-\Delta t}}{\sqrt{\alpha_{t-\Delta t}}}=\frac{\boldsymbol{x}_t}{\sqrt{\alpha_t}}+\left(\sqrt{\frac{1-\alpha_{t-\Delta t}}{\alpha_{t-\Delta t}}}-\sqrt{\frac{1-\alpha_t}{\alpha_t}}\right) \epsilon_\theta^{(t)}\left(\boldsymbol{x}_t\right)
\end{equation}
$$
这里拿$t-1$ 推广到$t - \Delta t$, $\alpha_t$ 推广到$\alpha_{t - \Delta t}$, 且令$\sigma=0$, 带进去推一下就能得到了, 过程略.
记$\sigma = \frac{\sqrt{1-\alpha}}{\sqrt{\alpha}}, \bar{\boldsymbol{x}} = \frac{\boldsymbol{x}}{\sqrt{\alpha}}$. 在连续条件下, $\sigma, \boldsymbol{x}$ 都为$t$ 的函数, 上式重写为:
$$
\bar{\boldsymbol{x}}(t-\Delta t)=\bar{\boldsymbol{x}}(t)+(\sigma(t-\Delta t)-\sigma(t)) \cdot \epsilon_\theta^{(t)}(\boldsymbol{x}(t))
$$
构造差分形式:
$$
\bar{\boldsymbol{x}}(t) - \bar{\boldsymbol{x}}(t-\Delta t)=(\sigma(t) - \sigma(t-\Delta t) \cdot \epsilon_\theta^{(t)}(\boldsymbol{x}(t))
$$
当$\Delta t \rightarrow 0$ 时, 有差分转换为微分:
$$
\mathrm{d} \bar{\boldsymbol{x}}(t)=\epsilon_\theta^{(t)}(\boldsymbol{x}_t)\mathrm{d} \sigma(t)
$$
将$\boldsymbol{x}_{t}$ 用$\bar{\boldsymbol{x}}(t), \sigma(t)$ 表示, 有:
$$
\begin{gathered}
\boldsymbol{x}_t = \sqrt{\alpha} \cdot \bar{\boldsymbol{x}}(t), \quad \sqrt{\alpha} = \frac{1}{\sqrt{\sigma^2(t) + 1}} \\\
\Downarrow \\
\boldsymbol{x}_{t} = \frac{\bar{\boldsymbol{x}}(t)}{\sqrt{\sigma^2(t)+1}}
\end{gathered}
$$
代入微分方程得:
$$
\mathrm{d} \bar{\boldsymbol{x}}(t)=\epsilon_\theta^{(t)}\left(\frac{\bar{\boldsymbol{x}}(t)}{\sqrt{\sigma^2+1}}\right) \mathrm{d} \sigma(t)
$$
因此, DDIM的迭代去噪过程可以被写成是一个Neural ODE. 它对应着一个向量场, 这意味着在这个场中任意粒子的运动轨迹都是确定与可逆的.
初始条件为$\boldsymbol{x}(T) \sim \mathcal{N}(0, \sigma(T))$, 其中$\sigma(T)$ 是一个非常大的值, 这对应着$\alpha \approx 0$ 的情况. 这意味着只要离散步足够多, 离散近似连续, 在这个Neural ODE中是可以按沿着Generative Process的逆向轨迹将$\boldsymbol{x}_0$ 转换为$\boldsymbol{x}_T$ 的, 在某些需要Latent Variable的下游任务中这一性质可能是有用的.
不过注意哈, DDIM的跳步步长肯定是不能选的太大的. 一方面是步长太大对$\boldsymbol{x}_{0}$的估计会不准, 多步错误累加会特别严重, 另外一方面是, 如果步长选的太大, DDIM就不能看成ODE了, 从而导致不再可逆.
Experiments
详细的模型参数设置和实验设置请参考原论文.
在实验部分都没有对DDPM的模型重新训练, 直接将训练好的DDPM复用, 原DDPM模型设置$T=1000$.
作者将DDIM中的标准差$\sigma$ 设定为与DDPM兼容的形式, 对DDPM前面乘上一个可控系数$\eta \in \mathbb{R}_{\geq 0}$:
$$
\begin{equation}
\sigma_{\tau_i}(\eta)=\eta \sqrt{\frac{1-\alpha_{\tau_{i-1}}}{1-\alpha_{\tau_i}}}\sqrt{1-\frac{\alpha_{\tau_i}}{\alpha_{\tau_{i-1}}}}
\end{equation}
$$
当$\eta=0$ 时为代表确定性的DDIM, $\eta=1$ 时为代表随机性的DDPM.
作者也考虑了随机噪声标准差大于$\sigma(1)$ 的情况, 用$\hat{\sigma}: \hat{\sigma}_{\tau_i} = \sqrt{1-\alpha_{\tau_i} / \alpha_{\tau_{i-1}}}$ 来表示.
考虑到不同的子序列$\tau$ 的取法可能会对结果产生影响. 对于希望的推理步长$\text{dim}(\tau) < T$, 作者也采用了两种不同的$\tau$ 的采样方式:
- Linear: 按照$\tau_i = \lfloor ci \rfloor$选择时间步, 在CIFAR10上采用.
- Quadratic: 按照$\tau_i = \lfloor ci^2 \rfloor$选择时间步, 在其余数据集上采用.
$c$ 为常数, 能够使得$\tau_{-1}$ 与$T$ 接近.
Sample Quality and Efficiency
DDIM($\eta=0$)和DDPM($\eta=1$)在CIFAR10(Linear)和CelebA(Quadratic)上的FID如下:
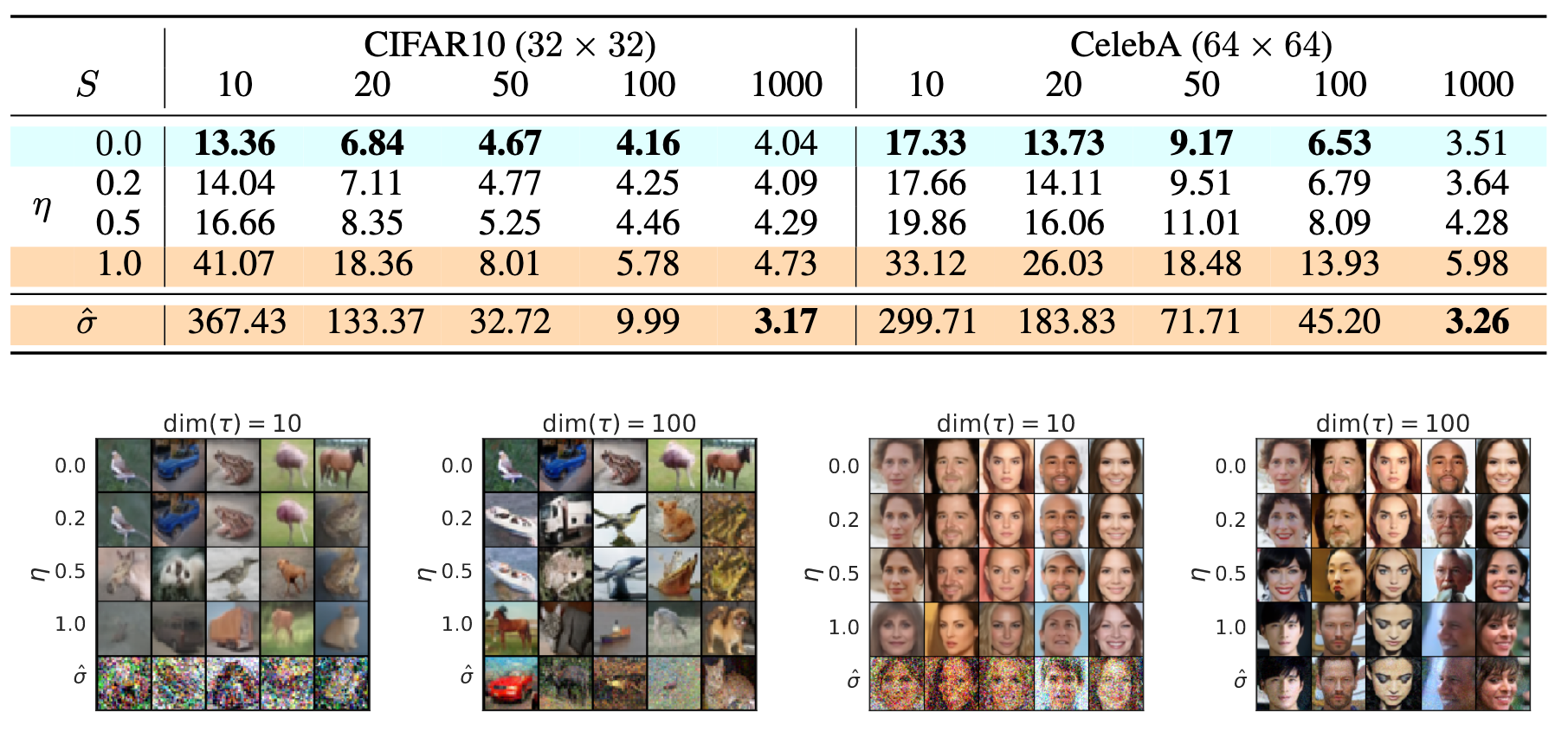
图中的$\text{dim}(\tau)$ 代采样步数$S$.
从表结果知, 对比DDIM和DDPM, DDIM在Step较小的时候($S \leq 100$)就可以取得比DDPM要好的多的效果. 不管是对Linear还是Quadratic, 结论基本不会变, 这基本上说明DDPM训练的时候每个Timestep Denoising也是因均匀采样而充分训练的, 进而再次证明了从中采样的子序列$\tau$ 是有效的.
但当时间步足够大($T=1000$)时, 反而较大噪声标准差的DDPM($\hat{\sigma}$)能取得更好的效果.
从图结果知, 当采样步数相对少的时候DDIM具有很高的样本质量. DDPM($\eta=1, \hat{\sigma}$)在$\text{dim}(\tau)=10$ 时受到噪声的影响要大得多, 样本质量很低.
DDIM的采样步数少, 自然而然采样成本也就压下来了:
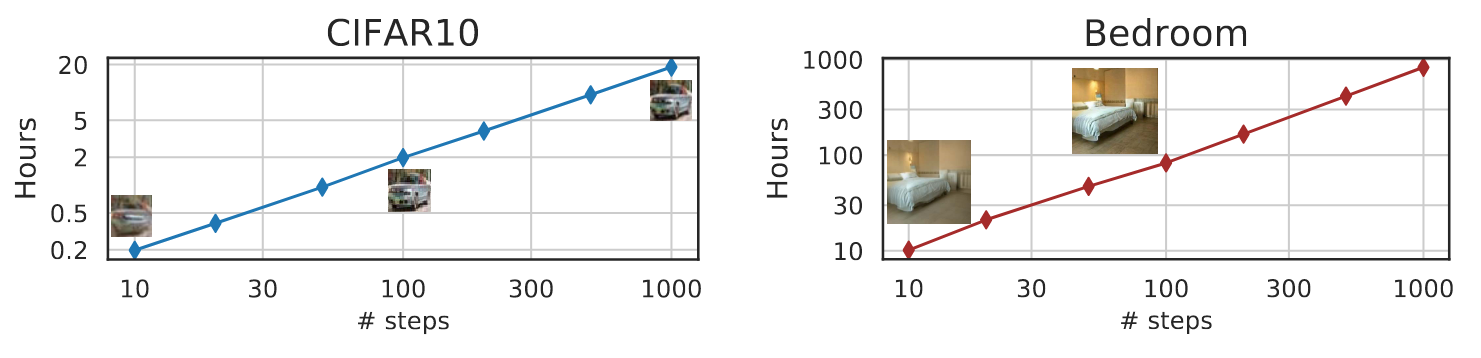
在100Steps的时候效果就已经很不错了, 采样那么多步也就没什么必要.
Sample Consistency in DDIMs
理论上的DDIM的生成过程是确定性的, 因为$\boldsymbol{x}_0$ 仅依赖于$\boldsymbol{x}_T$. 对于DDIM来说, 不同的$\text{dim}(\tau)$ 的选择意味着不同的生成轨迹. DDIM在相同的$\boldsymbol{x}_T$ 下, 不同轨迹$\tau$ 生成的图像几乎是一致的:

而且20步的结果基本上和1000步的相差不太多, 推理步长更大只会带来更多细节上的增益. 因此作者认为$\boldsymbol{x}_T$ 实际上已经可以作为一个信息丰富的Latent Encoding, 更多的细节被内化在模型参数$\theta$ 中.
Interpolation in Deterministic Generative Processes
如果$\sigma_t=0$ 的DDIM是一个能将某个随机噪声向量确定性的转化为某个样本的模型, 它实际上就与GAN几乎一样了. 所以结合GAN等模型的经验, 作者好奇是否对其进行插值会有类似GAN中出现的语义插值效果.
具体的, 将两个随机噪声$\boldsymbol{x}_{T}^{(0)}, \boldsymbol{x}_{T}^{(1)}$ 进行球面线性插值:
$$
\boldsymbol{x}_T^{(\alpha)} = \frac{\sin{\left((1-\alpha)\theta\right)}}{\sin{(\theta)}} \boldsymbol{x}_{T}^{(0)} + \frac{\sin{(\alpha\theta)}}{\sin{(\theta)}} \boldsymbol{x}_{T}^{(1)}
$$
其中$\theta = \arccos{(\frac{(\boldsymbol{x}_T^{(0)})^\top\boldsymbol{x}_T^{(1)}}{||\boldsymbol{x}_T^{(0)} || \cdot || \boldsymbol{x}_T^{(1)} ||})}$ .
然后就可以将得到的$\boldsymbol{x}_T^{(\alpha)}$ 用DDIM得到$\boldsymbol{x}_0$. 结果如下:

由于去除了DDPM中的随机生成过程, DDIM中可以在Latent中做语义插值. 而DDPM却不能做到这一点.
Reconstruction from Latent Space
前面说过, 当离散采样步数足够大的时候 ,DDIM可以被写成是一个Neural ODE, 轨迹是可逆的. 这就意味着可以用一个$\boldsymbol{x}_0$ 确定的得到一个$\boldsymbol{x}_{T}$. 作者在CIFAR10上进行了给定$\boldsymbol{x}_0$ 对$\boldsymbol{x}_T$ 的重建实验:

在步数足够多的时候, 重建误差是比较小的, 也就证明了此时轨迹是相对可逆的.
Recommended / Reference
- 比较推荐去看这个视频, 包含推导, 也比较易懂:
- 一些优秀的博客:
- 知乎上的一些文章:
- Huggingface diffusers库的代码实现, 注释写的很全:
Summary
DDIM构建了非马尔科夫的Forward Process与配套的Reverse Process / Generative Process, 并且其优化目标与DDPM完全一致(我在文中偷了个懒没有证), 因此可以直接复用训好的DDPM权重.
DDIM可以做到一些DDPM做不到的事情, 比如加速推理过程和确定性采样等. 如果只靠DDPM的资源消耗上确实很难绷. 如果DDPM $T=1000$, 那么DDIM就可以在维持图像生成质量的条件下只用20步生成, 达到50倍的加速效果. 这就更别说在建模更复杂任务时的效率了(比如出高清大图等).
现在的DDIM已经作为一项常见且实惠的技术内置在各类Diffusion Model中, 算是给DDPM续了一把火.

