本文前置知识:
- Flow Matching: Flow Matching for Generative Modeling.
或者:
Mean Flows for One-step Generative Modeling
- 论文: Mean Flows for One-step Generative Modeling, Kaiming He.
2025.05.20(北京时间)热乎出炉的工作, 主要引入了平均速度来提高单步生成效果:
MeanFlow
Flow Matching
首先来重温一下Flow Matching.
对于给定的数据分布$x \sim p_{\text{data}}(x)$ 和先验分布$\epsilon \sim p_{\text{prior}}(x)$, 对于时间$t$ 可以构造Flow Path $z_t = a_t x + b_t \epsilon$, $a_t, b_t$ 均由预定义的Scheduler决定, 一般取$a_t=(1-t), b_t=t$.
注意, 这里是将$z_1$ 定义为噪声, 而不是$z_0$, 后文同.
对于Flow Matching, 它的核心是学习一个速度场(ODE) $v_t=z^\prime_t = a_t^\prime x + b_t^\prime \epsilon$, 从而建模两个分布之间的传输过程:
$$
\frac{d}{d t} z_t = v(z_t, t)
$$
该过程始于$z_1 = \epsilon \sim p_{\text{prior}}$.
两边同时积分后, 它的解可以写成:
$$
z_t = z_r + \int_r^t v\left(z_\tau, \tau\right) d \tau
$$
即$z_r = z_t - \int_r^t v\left(z_\tau, \tau\right) d \tau$.
在解完这个ODE后, 可以用欧拉法来采样:
$$
z_{t_{i+1}} = z_{t_i} + (t_{i+1} - t_i) v(z_{t_i}, t_i)
$$
Flow Matching中用对条件速度场$v_t$ 的学习替换了对边缘速度场$v(z_t, t)$的学习:
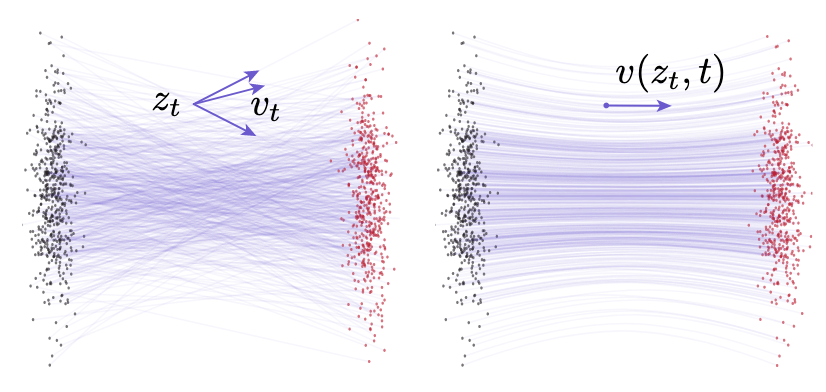
- 左侧: Conditional Flows. 通过给定的不同$(x, \epsilon)$ Pair, 学习条件速度场$v_t$, 能得到$x$ 在$t$ 时刻的多个不同的$z_t$. 所以Conditional Flow $v_t$ 学习的是已知分布到数据点之间的传输关系.
- 右侧: Marginal Flows. 将条件速度场中不同Pair对应的$z_t$ 求期望, 可以得到边缘速度场$v(z_t, t) \triangleq \mathbb{E}_{p_t(v_t|z_t)}[v_t]$, 所以$v(z_t, t)$学习的是已知分布到数据分布之间的传输关系.
上图中展示Conditional Flows / Marginal Flows都是Flow Matching里的瞬时速度场.
如果不知道这两个速度场之间的区别, 可以看下面这个图, 出自Meta的对Flow Matching的官方解读Flow Matching Guide and Code:
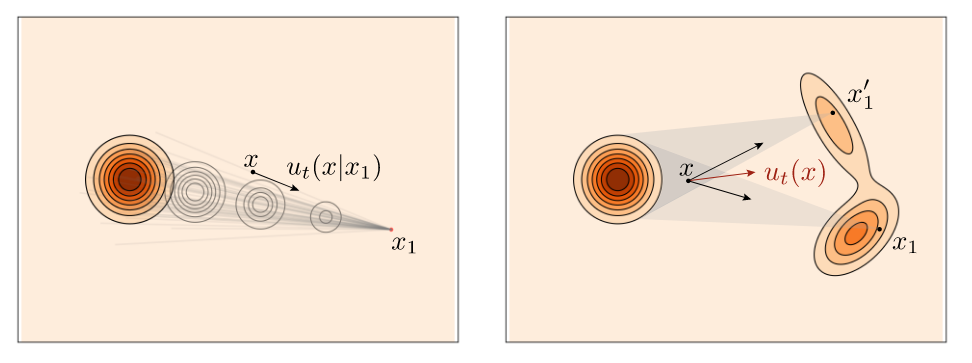
同样的, 左侧为条件速度场$u_t(x \mid x_1)$, 右侧为边缘速度场$u_t(x)$.
MeanFlow Models
平均速度就是对两个不同时间步$t$ 和$r$ 之间在速度场$v$ 内的积分, 并除以它们时间间隔$t-r$. 形式化上来说, 平均速度场$u$ 为:
$$
u\left(z_t, r, t\right) \triangleq \frac{1}{t-r} \int_r^t v\left(z_\tau, \tau\right) d \tau
$$
平均速度场$u(z, r, t)$ 应该长这个样子:
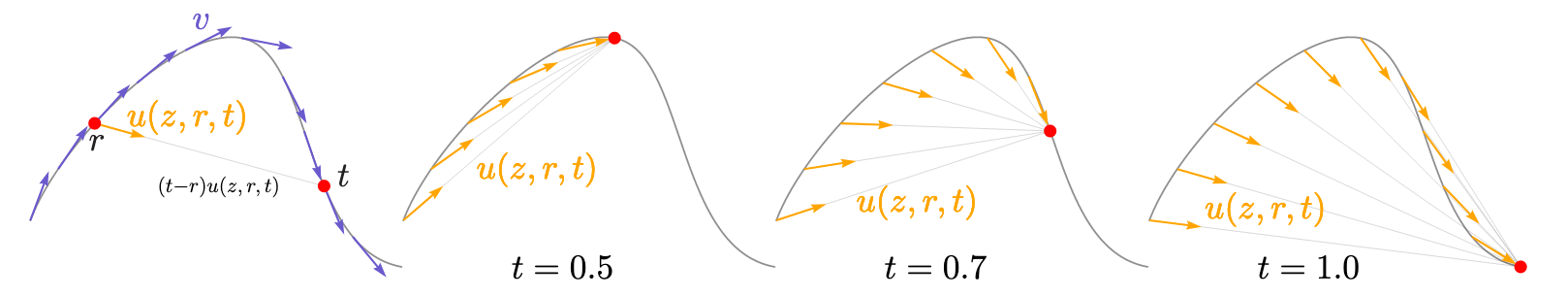
- 最左侧: 瞬时速度场$v$ 决定了路径的切线方向, 而平均速度$u$ 通常与瞬时速度$v$ 是不平行的. 但这段速度变化对应的位移一定是平行的, 因为位移是$(t-r)u(z, r, t)$.
- 右侧三图: 不同时间$t$ 对应的平均速度场.
从图上不难猜测出MeanFlow的核心思想, 是通过瞬时速度$v$ 学习一个从开始到结束平均速度$u(z, 0, 1)$, 然后完成一步生成, 从而达到加速的效果.
MeanFlow Identity
将平均速度场公式重写为:
$$
(t-r)u(z_t, r, t) = \int_r^t v(z_\tau, \tau) d \tau
$$
两边同时对时间求导, 有:
$$
\frac{d}{d t}(t-r) u\left(z_t, r, t\right)=\frac{d}{d t} \int_r^t v\left(z_\tau, \tau\right) d \tau \Longrightarrow u\left(z_t, r, t\right)+(t-r) \frac{d}{d t} u\left(z_t, r, t\right)=v\left(z_t, t\right)
$$
因此, 便得出了平均速度场$u$ 与瞬时速度场$v$ 的关系, 作者将其称为”MeanFlow Identity“:
$$
\underbrace{u\left(z_t, r, t\right)}_{\text {average vel. }}=\underbrace{v\left(z_t, t\right)}_{\text {instant. vel. }}-(t-r) \underbrace{\frac{d}{d t} u\left(z_t, r, t\right)}_{\text {time derivative }}
$$
这个式子非常简洁而且符合直觉, 平均速度$u$ 就是瞬时速度$v$ 减去对平均速度对时间的导数. 平均速度$u$ 就等于瞬时速度$v$ 减去在一段时间间隔$t-r$ 与期间对应的平均速度变化量$\frac{d}{d t} u\left(z_t, r, t\right)$ 之间的乘积.
平均速度$u$ 可以看做是瞬时速度$v$ 的一个函数, 即$u=\mathcal{F}[v]\triangleq\frac{1}{t-r}\int_r^tvd\tau$. 但是它不依赖于任何参数, 和Flow Matching一样, MeanFlow的想法就是用NN $u_\theta(z_t, r, t)$ 来学这个平均速度场$u$.
Computing Time Derivative
下面继续计算导数项$\frac{d}{d t}u$, 其偏导为:
$$
\frac{d}{d t} u\left(z_t, r, t\right) = \frac{d z_t}{dt}\partial_z u + \frac{d r}{dt}\partial_r u + \frac{d t}{dt}\partial_t u
$$
根据瞬时速度场$v$ 的ODE, 有$\frac{d z_t}{dt} = v(z_t, t)$, $\frac{dr}{dt}=0$, $\frac{dt}{dt}=1$, 因此得到:
$$
\frac{d}{d t} u\left(z_t, r, t\right) = v(z_t, t) \partial_z u + \partial_t u
$$
即函数$u$ 的雅可比阵$[\partial_z u, \partial_r u, \partial_t u]$ 在$[v, 0, 1]$ 方向上的方向导数.
Training with Average Velocity
类似于Flow Matching, MeanFlow的训练目标就是去拟合前面说的”MeanFlow Identity“.
在有了上面的推导后, MeanFlow的训练目标就是去拟合$u\left(z_t, r, t\right)$, 用瞬时速度$v$ 当做Ground Truth:
$$
\begin{gather}
\mathcal{L}(\theta) =\mathbb{E}\left\Vert u_\theta\left(z_t, r, t\right)-\operatorname{sg}\left(u_{\mathrm{tgt}}\right)\right\Vert _2^2 \\
u_{\mathrm{tgt}} =v\left(z_t, t\right)-(t-r)\left(v\left(z_t, t\right) \partial_z u_\theta+\partial_t u_\theta\right)
\end{gather}
$$
其中, $\text{sg}(\cdot)$ 为停止梯度运算符. 上式中的$v(z_t, t)$ 为Flow Matching里的边缘向量场.
仿照Flow Matching, 将边缘向量场用条件速度场$v_t = a^\prime_t x+ b^\prime_t \epsilon$ 替换, 目标为:
$$
u_{\mathrm{tgt}}=v_t-(t-r)\left(v_t \partial_z u_\theta+\partial_t u_\theta\right)
$$
当极端情况$t=r$ 时, 第二项消失, 此时的平均速度场$u_{\mathrm{tgt}}$ 学习目标为瞬时速度$v$.
采样则是直接将积分$\int_r^t v\left(z_\tau, \tau\right) d \tau$ 替换为平均速度得到的位移$(t - r)u(z_t, r, t)$:
$$
z_r = z_t - (t - r)u(z_t, r, t)
$$
对于一步生成的特殊Case, 直接取$r=0, t=1$ 的情况, 即$z_0 = z_1 - u(z_1, 0, 1)$. 其中$z_1 = \epsilon \sim p_\text{prior}(\epsilon)$.
所以从直观感觉上来说, 就是将采样时的瞬时速度$v$ 替换为了平均速度$u$. 同时, 在面对瞬时速度场变化不够剧烈的情况下, 由于平均速度变化更为平缓, 所以在采用较大的步长$t-r$ 作为时间间隔时速度方向更准确, 所以MeanFlow在采样步长较少的时候容易获得优势.
相应的, 在面对一些需要瞬时速度场动态变化的特性的任务上, 平均速度的使用也牺牲了这部分动态特性, 不过似乎可以通过对时间差$t-r$ 进行控制得到一些弥补.
虽然暂时没有公开代码, 不过伪代码里已经写的很明确了:
实现角度, 由于里面涉及到平均速度场$u$ 的导数项$\frac{d}{d t}u$, 作者采用torch.func.jvp直接计算偏导数$[\partial_z u, \partial_r u, \partial_t u]$ 在沿$[v, 0, 1]$ 方向的方向导数$v(z_t, t) \partial_z u + \partial_t u$.
u, dudt = jvp(fn, (z, r, t), (v, 0, 1))即分别计算函数fn在输入(z, r, t)的下对方向(v, 0, 1)的方向导数, 函数fn的输出结果为u, 偏导数项为dudt.
Mean Flows with Guidance
论文中还有一部分与CFG的说明, MeanFlow可以和CFG天然结合, 主要是我还没写博客, 所以这部分懒得看了… 感兴趣的自行看原论文.
Design Decisions
Loss Metrics
FM训练的时候采用L2 Loss. 但是根据一些Consistency Model的研究, 作者在计算Loss的时候同时附加上自适应权重, 权重$w=1/\left(\left\Vert \Delta \right\Vert_2^2 + c\right)^p$, 其中$p=1-\gamma$ 且$c>0$. 用于模型优化的Loss则为$\text{sg}(w)\cdot \left\Vert \Delta \right\Vert_2^2$.
Sampling Time Steps
对于要采样的两个时间步$(r, t)$来说, 有均匀分布$\mathcal{U}(0, 1)$ 和对数正态分布两种选择. 对数正态分布是先从正态分布$\mathcal{N}(\mu, \sigma)$ 中采样, 然后再用Sigmoid函数归一化到(0, 1)之间. 然后将大一点的值分配给$t$, 小一点的分配给$r$, 也会有一小部分有$r=t$.
Condition
作者用Positional Embedding来编码$(r, t)$ 的时间信息. 这里面就有点说法了, 因为$u_\theta(z_t, r, t)$ 虽然依赖于$(r, t)$, 但是可以不直接依赖于$(r, t)$, 比如引入$\Delta t=t-r$ , 让$(t, \Delta t)$ 作为模型的输入.
Experiments
Main Result
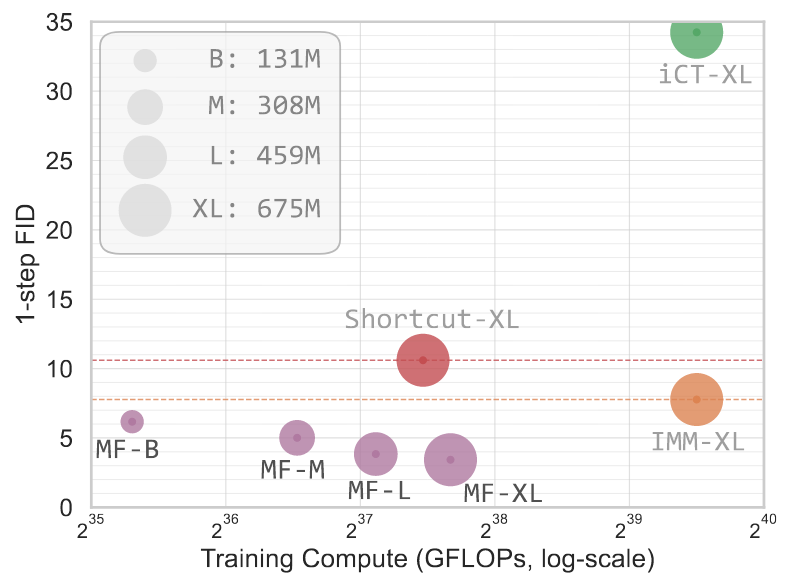
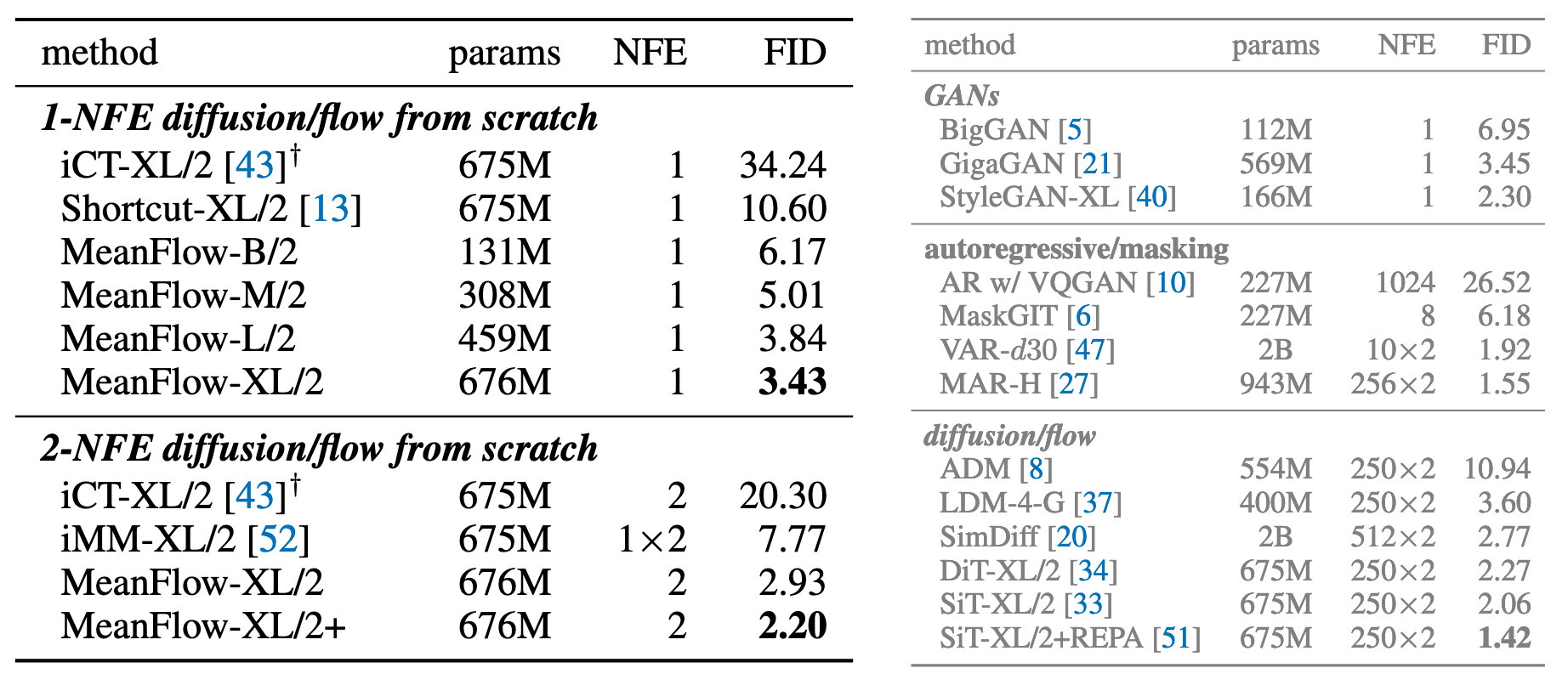
实验结果表明, MeanFlow能在一步或者两步的情况下与一些同规模采用更多步数的模型效果相当:
Ablation Study
下面是针对一些因素做的消融实验.
Ratio of sampling $r \neq t$:
0%, 即全部有$r=t$ 时, MeanFlow退化为Flow Matching, 已经没法完成一步生成了. 虽然在25%, 50%, 100%都可以做到一步生成, 但仅当有25%的$r\neq t$ 时能产生最好的一步生成效果.
这实验应该可以说明Flow Matching和MeanFlow之间存在一种可以做一步生成的平衡点, 但是为什么是25%感觉还可以深挖.
JVP computation:
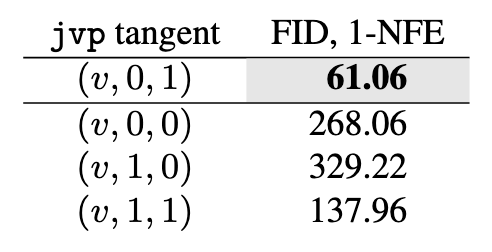
采用错误的JVP计算会导致非常差的效果, 仅当正确的Tangent存在时MeanFlow才能Work.
Positional Embedding:
使用什么总体上都不会有特别大的影响. 只使用$(t, r)$ 时就能使用相对好的性能, 但是在使用$(t, t-r)$ 时能取得最好的性能.
如果只使用$t-r$ 也是可以的, 这也说明了MeanFlow的平均速度场其实随时间变化在总体上比较平缓.
Time samplers:
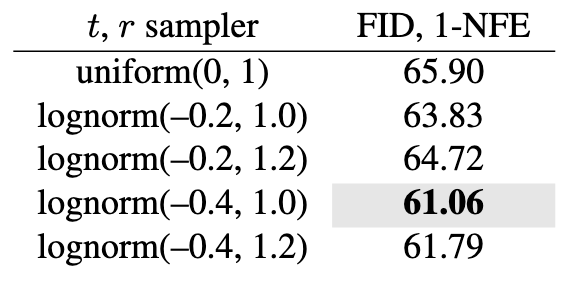
结果显示采用对数正态采样比较好, 和Flow Matching中的结论是一致的. 而且总体来看, 即使基于均匀分布采样, 也不会让模型结果变得很差.
Loss metrics:
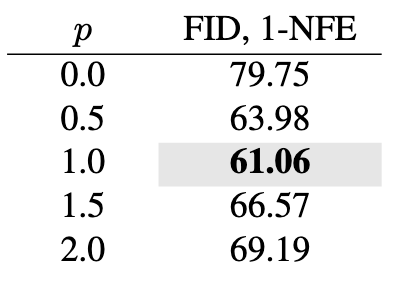
$p=1$ 时, 有$w=1/\left(\left\Vert \Delta \right\Vert_2^2 + c\right)$, 即MSE越大的项权重越小, 此时可以取得最好的效果.
CFG scale:
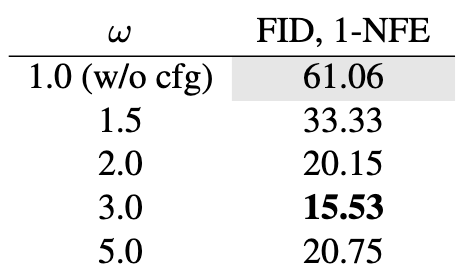
在不同的Guidance Scale下CFG都能增强MeanFlow单步生成的效果.
Scalability:
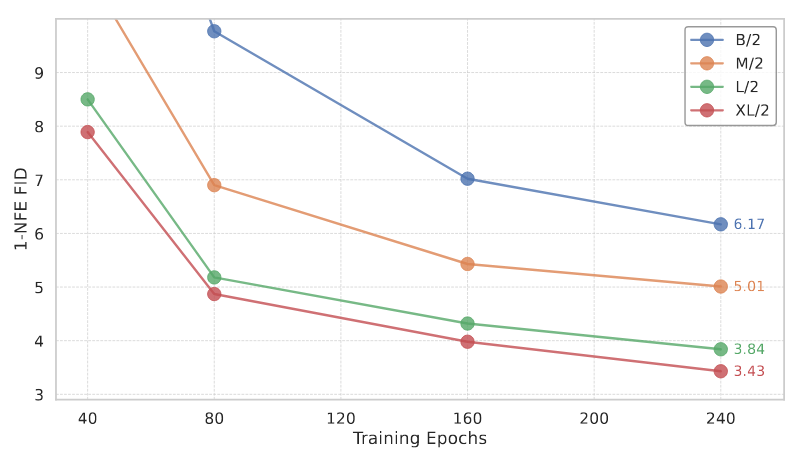
MeanFlow有Scaling到更大的规模的潜力.
Summary
MeanFlow通过引入平均速度来加速了在步长比较少的情况下的生成速度. 也是一个比较简洁的工作.
我个人认为, MeanFlow和Flow Matching之间存在一定的转化关系, 因此MeanFlow算是在Flow-based Model流行的时代一种加速推理的手段. 而且它也不难实现, 如果实际复现效果真的还可以的话, 感觉很多Flow-based Model都会实装, 期待在未来看到MeanFlow能发挥更大的作用.
