本文前置知识:
Contextual Parameter Generation for Knowledge Graph Link Prediction
本文是论文Contextual Parameter Generation for Knowledge Graph Link Prediction的阅读笔记和个人理解. 本文是CMU发布的参数生成系列论文中的一篇, 系列文章请参见参数生成(Parameter Generation/Adaption)相关论文整理.
Basic Idea
作者发现, 现在的KGE模型中Relation Embedding经常被限制为加性的, 这使得模型在处理不同关系变换时的表达能力被限制.
为解决此问题, 作者使用上下文参数生成方法, 去除掉加性限制. 更具体的, 作者将关系作为上下文来做Knowledge Embedding, 下图是作者改进ConvE的示意图:
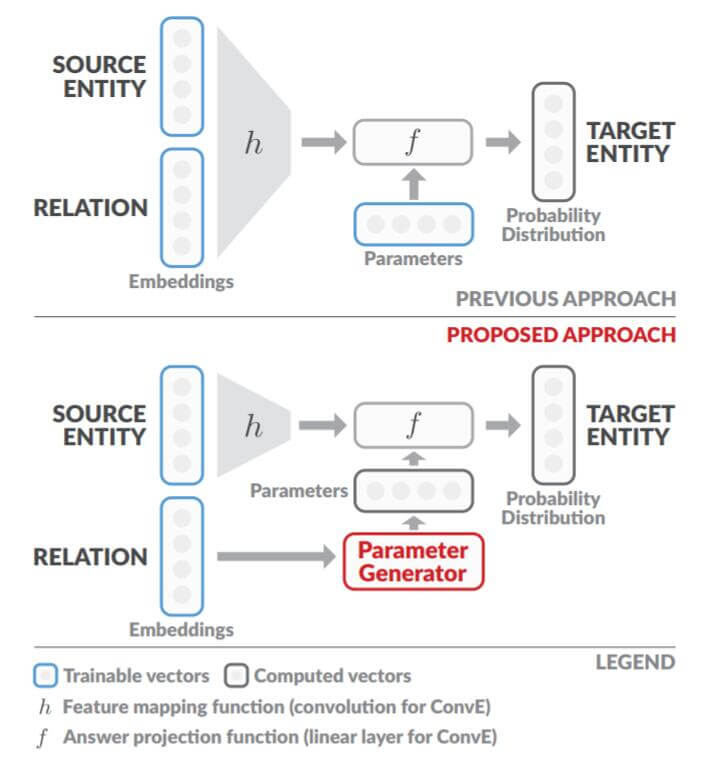
如图构想所示, Relation Embedding作为用于生成操作Entity Embedding的参数信息而存在. 这种方式被作者称为CoPER(Contextual Parameters from Embedded Relations).
Limited Expressive Power
现在Knowledge Embedding框架普遍可以由如下四部组成:
$$
\begin{array}{lr}
\mathbf{e}_{s}=\mathbf{E} e_{s}, &\quad \text { (embedding) }\\
\mathbf{r}=\mathbf{R} r, &\quad \text { (embedding) }\\
\mathbf{z}=h_{\phi}\left(\mathbf{e}_{s}, \mathbf{r}, \ldots\right), &\quad\text { (merge) }\\
\text {ans}=f_{\theta}(\mathbf{z}, \ldots), &\quad \text { (prediction) }
\end{array}
$$
其中$e_s , r$ 分别是头实体和关系的独热编码, $\mathbf{E}, \mathbf{R}$ 是实体和关系的Embedding矩阵. $h$ 为Merge Function, 参数为$\phi$, 用于获取关系和头实体的聚合表示. $f$ 为Prediction Function, 参数为$\theta$, 用于预测出尾实体.
四步可以概括为获取头实体表示, 获取关系表示, KGE聚合, 投影预测.
Merge和Prediction的具体操作在不同的KGE方法中通常是不同的, 作者以ConvE为例, 具体的说明了表达是如何被限制的. 在ConvE中, 后两步的数学表达如下:
$$
\begin{array}{lr}
\mathbf{z}=\operatorname{Conv2D}\left(\operatorname{Reshape}\left(\left[\mathbf{e}_{s} ; \mathbf{r}\right]\right)\right), & \text { (merge) } \\
\hat{e}_{t} =f_{\theta}(\mathbf{z}), & \text { (prediction) }
\end{array}
$$
ConvE中, Merge Function为将头实体和关系的嵌入表示Concat, 后Reshape成二维数据, 然后用二维卷积获取聚合后的表示$\mathbf{z}$, $f_\theta$ 为一次线性变换, 即$\theta$ 代表投影矩阵.
考虑一种最简单的情况, 当Merge Function为Concat + Linear时的场景:
$$
h_{\phi}\left(\mathbf{e}_{s}, \mathbf{r}\right)=\phi \cdot\left[\mathbf{e}_{s} ; \mathbf{r}\right]
$$
$[\cdot; \cdot]$ 为Concat, $\phi$ 为单层线性投影. 正是因为Concat在操作上使得$\mathbf{e}_s, \mathbf{r}$ 之间是相互独立的, $h_\phi (\mathbf{e}_s; \mathbf{r})$ 可以被写为$h_\phi (\mathbf{e}_s; \mathbf{r})=\phi_s \mathbf{e}_s + \phi_r\mathbf{r}$, 所以$\mathbf{e}_s, \mathbf{r}$ 只能做加性交互. ConvE在大多数情况下都符合上述情况, 唯独除了卷积核在对$\mathbf{e}_s$ 和$\mathbf{r}$ 的交界处做交互的情况.
作者所提出的问题仅适用于ConvE这种没有进行模块堆叠的方法, 因为ConvE仅仅只使用了一层卷积.
同样也不适用于能够同时覆盖$\mathbf{e}_o$ 和$\mathbf{e}_r$ 的操作. 如果操作能够覆盖二者, 那么二者之间将不单进行简单的加和运算, 还会有其他部分的交互运算.
如果是多层卷积堆叠, 随着堆叠加深, $\mathbf{e}_s$ 和$\mathbf{r}$ 交界处所映射的范围也越来越大, 直到感受野可以覆盖住整个特征图, 每次卷积都可以对整块数据交互, 即使是使用了Concat, 也不符合作者所述的情况.
作者举出了一个非常简单的例子(Toy Example)来详细说明一些KGE模型在应对这些场景时所暴露的问题:
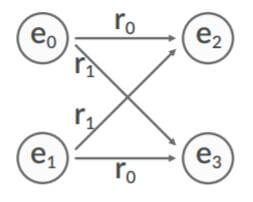
如果以三元组作为结构, 那么$\mathbf{e_2}, \mathbf{e_3}$ 可以按照如下方式表示:
$$
\begin{array}{l}
\mathbf{e}_{2}=\phi_{e} \mathbf{e}_{0}+\phi_{r} \mathbf{r}_{0} \\
\mathbf{e}_{3}=\phi_{e} \mathbf{e}_{0}+\phi_{r} \mathbf{r}_{1} \\
\mathbf{e}_{3}=\phi_{e} \mathbf{e}_{1}+\phi_{r} \mathbf{r}_{0} \\
\mathbf{e}_{2}=\phi_{e} \mathbf{e}_{1}+\phi_{r} \mathbf{r}_{1}
\end{array}
$$
将上述四个式子可以分别做减法得到如下两个$\mathbf{e}_2, \mathbf{e}_3$ 的表示式:
$$
\begin{array}{l}
\left(\mathbf{e}_{2}-\mathbf{e}_{3}\right)=\phi_{r}\left(\mathbf{r}_{0}-\mathbf{r}_{1}\right) \\
\left(\mathbf{e}_{3}-\mathbf{e}_{2}\right)=\phi_{r}\left(\mathbf{r}_{0}-\mathbf{r}_{1}\right)
\end{array}
$$
这两个表示式非常的矛盾, 除非满足如下情况:
- $\mathbf{e}_2 = \mathbf{e}_3$: 将导致$\mathbf{e}_2, \mathbf{e}_3$无法区分.
- $\phi_r=0$ 或$\mathbf{r}_0 = \mathbf{r}_1$: 将导致$\mathbf{r}_1, \mathbf{r}_2$ 无法区分或失效.
- $\phi_e=0$ 或$\mathbf{e}_0 = \mathbf{e}_1$: 将导致$\mathbf{e}_0, \mathbf{e}_1$ 无法区分.
即模型无法处理Toy Example的情况. 主要原因就在于, 虽然Merge Function操作对象表面是$\mathbf{e}_s$ 和$\mathbf{r}$, 但做后续操作的时候还是近似对它们单独处理的.
CoPER
在CoPER中, Relation被定义为, 为了产生尾实体, 应该对头实体进行何种操作. 因此, $h$ 只作用于$\mathbf{e}_s$, 而$\mathbf{r}$ 将用于生成$f$ 的参数$\theta$. $f$ 的参数将不再由学习得来, 而由CPG(Contextual Parameter Gneration)模块的输出得来, CPG是一种能够对于给定的Relation独热编码$r$ 给出操作头实体的参数$\theta$ 的模块.
Parameter Generator Network
有多种方式可以通过$r$ 来获取$\theta$. 最简单的一种是通过查表:
$$
g_{\text {lookup }}(r)=\mathbf{W}_{\text {lookup }} r
$$
但是这种方式不能在跨关系时实现信息共享, 而且非常容易过拟合, 尤其是面对训练集中所出现的关系.
换一种方法, 也可以是简单的Linear Projection:
$$
g_{\text {linear }}(r)=\mathbf{W}_{\text {linear }} \mathbf{R} r+\mathbf{b}
$$
这样, 通过一个权重矩阵$\mathbf{W}$, 不同的关系嵌入$\mathbf{r}$ 可能共享一些潜在的共性, 因为$\mathbf{r}$ 会被重新线性组合.
一般非常大的线性变换矩阵很容易造成过拟合, 而MLP可以作为一种线性变换的低秩近似:
$$
g_{\mathrm{MLP}}(r)=\operatorname{MLP}(\mathbf{R} r)
$$
当然也可以是其他更复杂的结构, 这里只列举了最简单的三种.
Enhanced Expressive Power
其实作者的解决思路非常的简朴, 把加性变成乘性的不就完了么. 还是针对前面的Toy Example, 构建最简单的情况. 假设Merge Function有$h_\phi(\mathbf{e}_s)=\mathbf{e}_s$, $f$ 是最简单的线性投影, 即$f_\theta(x)=\theta x$, $\theta=g_{\text{linear}}(r)=\mathbf{WR}r+\mathbf{b}=\mathbf{Wr}+b$, 因此:
$$
\hat{e}_{t}=f_{\theta}\left(h_{\phi}\left(\mathbf{e}_{s}\right)\right)=f_{\theta}\left(\mathbf{e}_{s}\right)=\theta \mathbf{e}_{s}=(\mathbf{W r}+\mathbf{b}) \mathbf{e}_{\mathbf{s}}
$$
这使得Relation Embedding将以乘性地作用于$\mathbf{e}_s$, Toy Example重新表示为如下四个式子:
$$
\begin{array}{l}
\mathbf{e}_{2}=\left(\mathbf{W r}_{0}+\mathbf{b}\right) \mathbf{e}_{0} \\
\mathbf{e}_{3}=\left(\mathbf{W r}_{0}+\mathbf{b}\right) \mathbf{e}_{1} \\
\mathbf{e}_{2}=\left(\mathbf{W} \mathbf{r}_{1}+\mathbf{b}\right) \mathbf{e}_{1} \\
\mathbf{e}_{3}=\left(\mathbf{W} \mathbf{r}_{1}+\mathbf{b}\right) \mathbf{e}_{0}
\end{array}
$$
还是将上式做减法, 能得出在两个三元组下的表示结果是不同的:
$$
\begin{array}{l}
\mathbf{e}_{3}-\mathbf{e}_{2}=\left(\mathbf{W r}_{0}+\mathbf{b}\right)\left(\mathbf{e}_{1}-\mathbf{e}_{0}\right) \\
\mathbf{e}_{3}-\mathbf{e}_{2}=\left(\mathbf{W} \mathbf{r}_{1}+\mathbf{b}\right)\left(\mathbf{e}_{0}-\mathbf{e}_{1}\right)
\end{array}
$$
除去一组解$\mathbf{e}_0=\mathbf{e}_1$, 其他解都可以使得该式有意义:
$$
\mathbf{W}\left(\mathbf{e}_{1}-\mathbf{e}_{0}\right)\left(\mathbf{r}_{0}+\mathbf{r}_{1}\right)+2 \mathbf{b}\left(\mathbf{e}_{1}-\mathbf{e}_{0}\right)=0
$$
因此, $\mathbf{e}_2, \mathbf{e}_3$ 找到了更合适的表示.
CoPER - ConvE
基于上述方法, 作者将ConvE改写为如下过程:
$$
\begin{aligned}
\mathbf{z} &=\operatorname{Conv2D}\left(\operatorname{Reshape}\left(\mathbf{e}_{s}\right)\right)\\
\theta &=g(r)\\
\hat{e}_{t} &=f_{\theta}(\mathbf{z})=\theta_{1}+\theta_{2: D_{\theta}} \mathbf{z}
\end{aligned}
$$
即投影层的参数是由$\mathbf{r}$ 生成的, $\theta_1, \theta_2$ 是由$\theta$ 分割而来, 即$\theta = [\theta_1; \theta_2]$.
CoPER - MINERVA
同样, 对于基于LSTM的方法MINERVA也可以改写为下述式子:
$$
\mathbf{h}_{i}=\mathbf{L S T M}\left(\mathbf{h}_{i-1},\left[\mathbf{e}_{i} ; \mathbf{r}_{i-1}\right]\right)
$$
$$
\begin{array}{lr}
\mathbf{o}_{i}=\operatorname{MLP}\left(\left[\mathbf{h}_{i} ; \mathbf{e}_{i} ; \mathbf{r}_{q}\right]\right), &\quad \text { (merge) }\\
a_{j}=\operatorname{Categorical}\left(\mathbf{A}_{i} \mathbf{o}_{i}\right)&\quad \text { (prediction) }
\end{array}
$$
这个模型不是很了解, 在此不做说明了.
上述两种方法更改前与更改后的对比图如下:
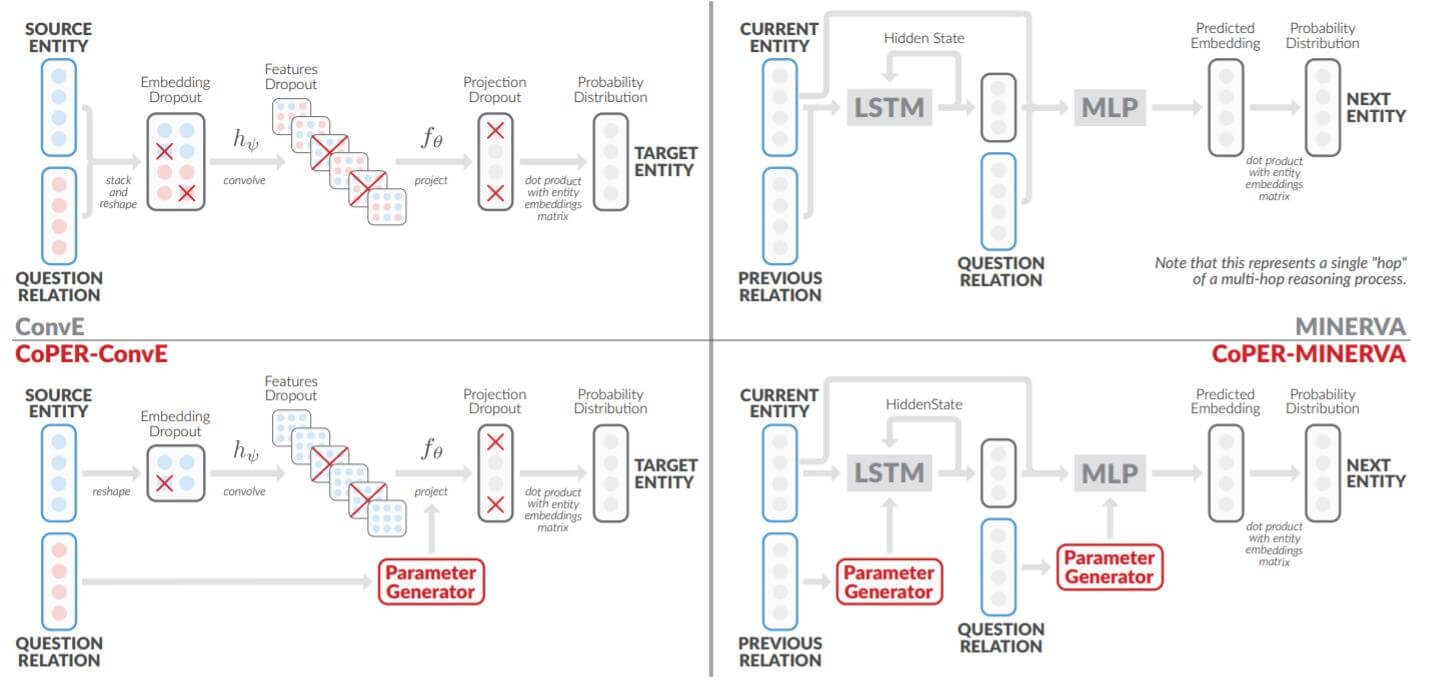
主要区别在于不将实体嵌入和关系嵌入一起输入模型, 仅将关系嵌入作为对头实体嵌入操作参数生成的依据.
Experiments
作者将当前SOTA的模型在五个常用数据集上做了实验, 统计信息如下:
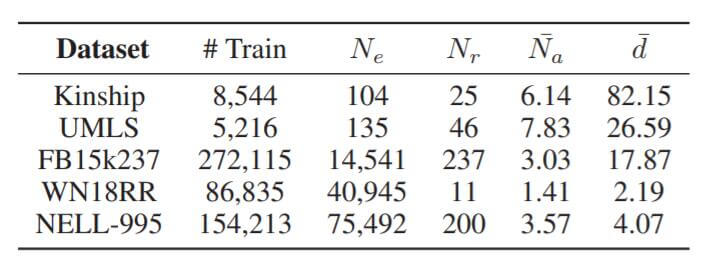
$N_e$ 为实体数量, $N_r$ 为关系数量, $\tilde{N}_a$ 为每个问题平均的答案数量, $\tilde{d}$ 为平均节点度.
下面是实验结果:
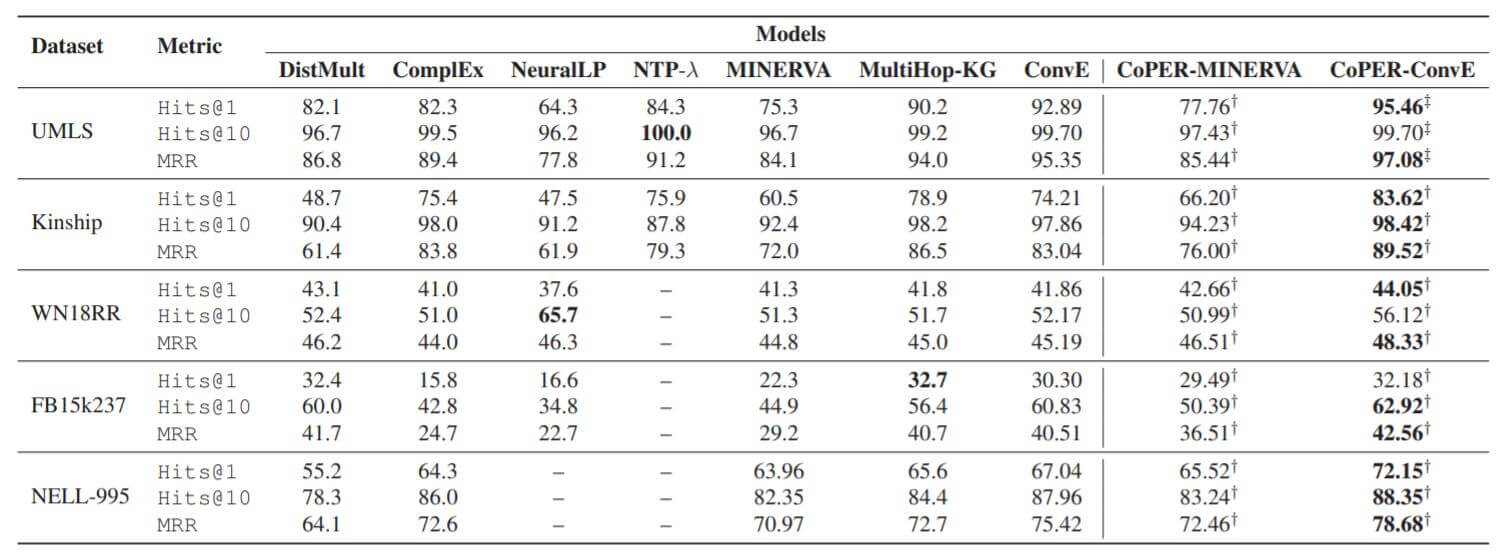
效果显著的变好了, 涨点特别多.
除涨点外, 最为显著的是其收敛提速效果:
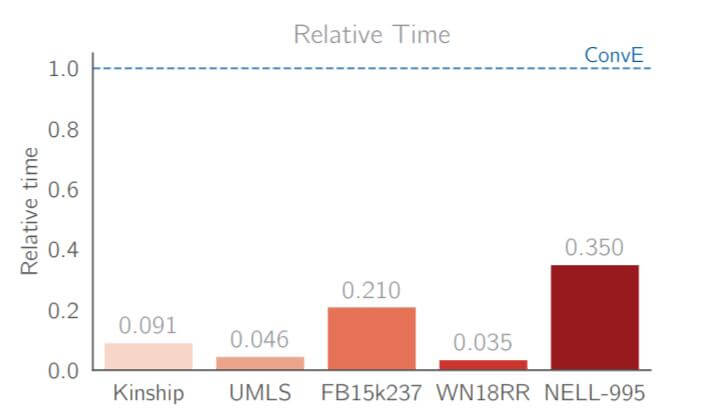
在不将实体嵌入和关系嵌入一并Merge过后, 收敛提速效果极其明显. 但是加速效果具体应该有多少似乎与数据集没有固定的规律.
消融实验结果如下:
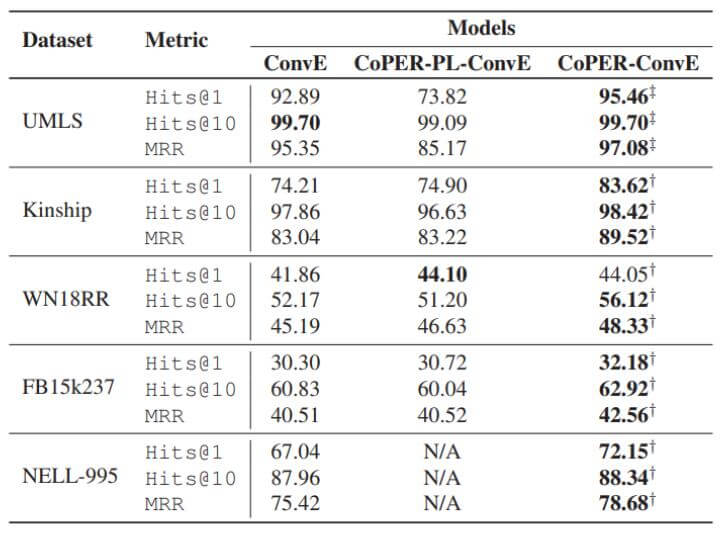
“CoPER - PL - ConvE”代表作者前面所述的查表的方法. 而CoPER指的是使用$g_{\text{linear}}$ 或者$g_{\text{MLP}}$ 的方法.
Summary
CoPER针对作者提出的场景解决方法简单而有效, 将参数生成应用到链接预测任务上, 将关系视为上下文, 生成操作头实体的函数参数.
但作者的方法仅能用于改进无交互性操作的模型, 例如ConvE等.
这篇论文其实可以与类似的方法ConvR进行对比, 这二者同样都可以针对ConvE做出改进, 也同样都是对关系的特化处理.
ConvR侧重于从结构的角度将关系嵌入直接作为卷积核, 而CoPER - ConvE将关系嵌入作为参数生成的上下文依据, 生成投影所需的参数.
所以甚至可以集二者之优, 沿着CoPER中参数生成的思路去改进ConvR? 或许一定程度上可以缓解ConvR中关系嵌入没有深层次化的问题.

