本文前置知识:
ConvR: Adaptive Convolution for Multi-Relational Learning
本文是论文Adaptive Convolution for Multi-Relational Learning的阅读笔记和个人理解.
Basic Idea
即使ConvE在KGE上利用CNN取得了突破性的成就, 但它的设计仍然忽略了实体和关系之间的交互性, 限制了Link Prediction的性能.
在ConvE中, 是将头实体和关系Reshape, 然后用标准卷积的卷积核进行运算, 而实际包含有实体和关系Embedding交互的只有卷积核经过的中间那一条(图中用红色标出):
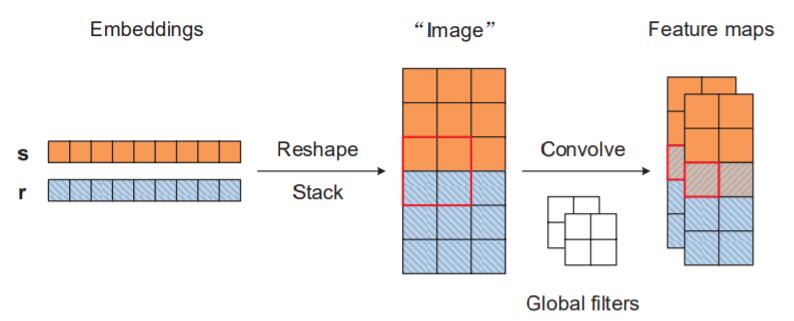
少量的交互次数使得关系对实体Embedding的影响降低了许多, 如果能进一步提升交互应该能改善性能.
因此, 作者同样是希望利用卷积, 最大化实体和关系间的交互次数, 从而提升卷积类模型在链接预测的性能.
ConvR
ConvR其实非常简单, 它仍然没有脱离ConvE的框架. 它仅仅只是将卷积核直接拿掉了, “关系就是卷积核“.
ConvR的精髓在于, 适应性的将Relation Embedding构建成卷积核, 与Entity Embedding交互:
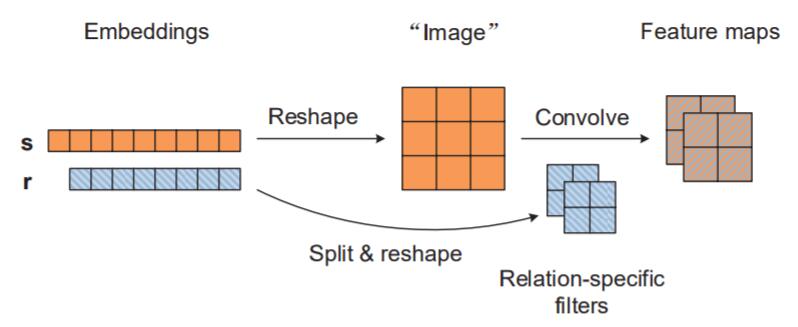
这样每次卷积都是100%的交互.
The ConvR Model
与ConvE一样, 先将Entity Embedding Reshape成2D矩阵$\mathbf{S} \in \mathbb{R}_{e}^{d_{e}^{h} \times d_{e}^{w}}$, 且$d_e = d_e^h d_e^w$. 在ConvE中已经论证过在2D上做卷积运算比1D卷积的优越性了.
然后需要用Relation Embedding构建成卷积核. 首先将Relation Embedding划分为大小相同的若干小块$\mathbf{r}^{(1)}, \cdots, \mathbf{r}^{(c)}$, 该过程称为Split.
因为是2D卷积, 对于每个小块$\mathbf{r}^{(\ell)} \in \mathbb{R}^{d_{r} / c}$, 都重新Reshape成高$h$, 宽$w$ 的卷积核$\mathbf{R}^{(\ell)} \in \mathbb{R}^{h \times w}$, $d_{r}=chw$.
若拿$chw$ 作为$d_r$, 可能导致维数过大.
在卷积时就采用关系特化的卷积核$\mathbf{R}^{(\ell)}$进行运算, 卷积过程的数学表示如下:
$$
c_{m, n}^{(\ell)}=f\left(\sum_{i, j} s_{m+i-1, n+j-1} \times r_{i, j}^{(\ell)}\right)
$$
其中$f$ 为非线性函数. 每个卷积核都能产生大小为$\mathbb{R}^{\left(d_{e}^{h}-h+1\right) \times\left(d_{e}^{w}-w+1\right)}$ 的特征图$\mathbf{C}^{(\ell)}$:
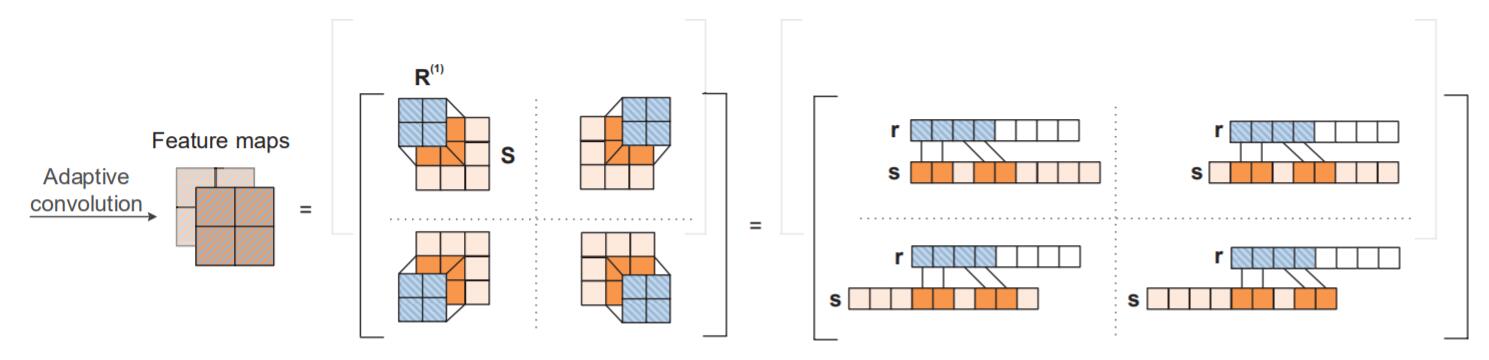
最后, 将前面卷积产生的所有特征图$\mathbf{C}^{(1)}, \cdots, \mathbf{C}^{(c)}$全部打平, 然后堆叠成一个向量$\mathbf{c}$, 然后通过一个投影层将其转化为大小为$\mathbb{R}^{d_{e}}$ 的向量, 与尾实体向量$\mathbf{o}$ 做点积, 打分函数如下:
$$
\psi(s, r, o)=f(\mathbf{W} \mathbf{c}+\mathbf{b})^{\top} \mathbf{o}
$$
其中$\mathbf{W} \in \mathbb{R}^{d_{e} \times c\left(d_{e}^{h}-h+1\right)\left(d_{e}^{w}-w+1\right)}$, $\mathbf{b} \in \mathbb{R}^{d_{e}}$. 形式与ConvE完全一致.
Parameter Learning
首先计算尾实体的概率:
$$
p_{o}^{s, r}=\sigma(\psi(s, r, o))
$$
其中$\sigma$ 是对数几率函数, 即$\sigma(x)=\frac{1}{1+e^{-x}}$.
与ConvE提出的1 - n Scoring相同, 然后用二分类交叉熵(BCE)损失函数进行优化:
$$
\mathcal{L}(s, r)=- \frac{1}{|\mathcal{E}|} \sum_{o \in \mathcal{E}} y_{o}^{s, r} \log \left(p_{o}^{s, r}\right)+
\left(1-y_{o}^{s, r}\right) \log \left(1-p_{o}^{s, r}\right)
$$
其他小Trick例如Dropout, BN, Label Smoothing仍然沿用ConvE.
Advantages over ConvE
既然是ConvE的优化方法, 作者将着重论证ConvR比ConvE的优越性. 主要有两点:
交互次数比ConvE变多了, 每次卷积都是Entity Embedding和Relation Embedding的交互.
参数比ConvE少了, 因为”关系就是卷积核“.
ConvE:$\mathcal{O}\left(d|\mathcal{E}|+d|\mathcal{R}|+c h w+c d\left(2 d^{h}-h+1\right)\left(d^{w}- w + 1\right)\right)$
ConvR: $\mathcal{O}\left(d_{e}|\mathcal{E}|+d_{r}|\mathcal{R}|+c d_{e}\left(d_{e}^{h}-h+1\right)\left(d_{e}^{w}-w+1\right)\right)$
ConvR少掉的部分$chw$ 被集成进了Relation Embedding中.
Experiments
详细的实验参数设置请参照原论文.
Link Prediction Results
作者主要探究了ConvR在WN18, FB15K, WN18RR, FB15K - 237上的性能:
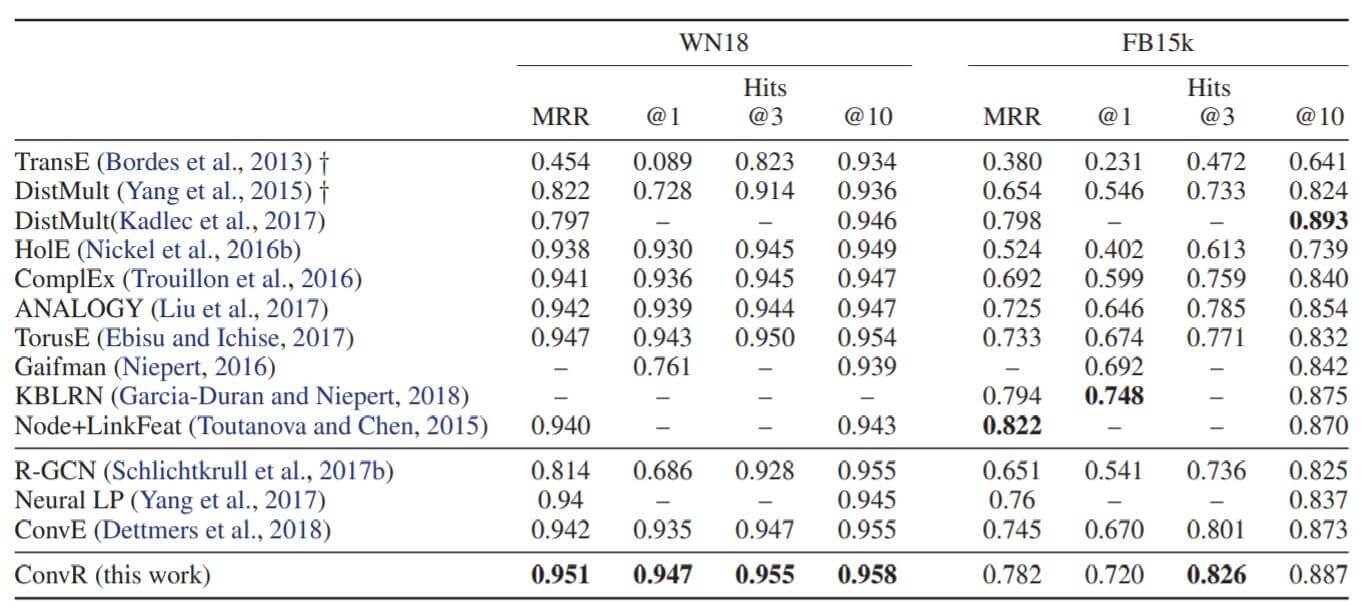
WN18和FB15K这两个数据集是存在大量逆关系的, 结果可能是过拟合了的.

主要的对比还是集中在卷积类的模型, ConvR比ConvE有了小幅提升, 比ConvKB的效果也要好.
其中所采用的最佳配置如下:

能看到, 如果使用ConvR, $d_r=chw$, 在列出的最佳结果中$d_r$ 都是远比$d_e$ 大的.
Parameter Efficiency
作者探究了不同卷积核大小和不同数量对模型性能的影响:

总体来说各类参数对性能影响不大, 可以认为算法对超参是比较不敏感的.
Summary
从卷积核自身结构下手, 与关系信息融合是一个非常好的思路. ConvR的设计即减少了参数量, 也增加了实体关系嵌入的交互次数.
但是以结构为基础的融合也是一把双刃剑, 我认为ConvR还存在两个重要的问题:
- 虽然提升了关系和实体之间的交互次数, 但受制于直接拿关系Embedding作为卷积核的方式, ConvR无法像其他卷积类方法把模型做得更深. 一般来讲, 卷积层数越深, 所抽取到的特征也就越高阶, 也就意味着更复杂的实体与关系交互, 但在ConvR中只能做一层卷积.
- 因为卷积的特殊机制, $d_e$ 和$d_r$ 大概率不相同, 可能会对下游任务使用产生一定影响(许多场景要求$d_e$ 和$d_r$ 是相同维度的, 所以还需要额外维度压缩). 作者所给出的示例$d_r$ 都比较大, 如果强行调整至一致可能会导致性能衰减.

