本文前置知识:

• Transformer(Masked Self - Attention和FFN)
• BERT(与XLNet做对比)
• Seq2Seq(AutoRegressive & AutoEncoding)

2020.10.26: 更新了Transformer - XL的隐态更新维度分析.

Transformer - XL与XLNet

本文是Transformer - XL和XLNet论文的阅读笔记和个人理解(实际上还包括Vanilla Transformer).

Background

这两篇论文都没有从Transformer开始, 而是从Character-Level Language Modeling with Deeper Self-Attention开始, 该模型利用了Self - Attention在更深层次的语言模型上进行字符级建模, 因内容比单词级更长, 所以提出了直接将内容按照固定大小划分为Segment处理的方法. 该在文中被称为Vanilla Transformer, 被多次提及. 分段的方式伴随着多种缺点, Vanilla Transformer对Segment的划分没有进行任何优化. 而Transformer - XL对该模型存在的问题进行了优化, 而XLNet将Transformer - XL和BERT的优势结合到了一起.

Vanilla Transformer

中使用的Transformer被称为Vanilla Transformer(普通Transformer). 我们只需要知道它将一个Masked 多头Self - Attention和一个由两层全连接构成的FFN称为一个Transformer Layer, 然后堆叠多层Transformer Layer. 训练时使用语言模型的方式, 采用字符级数据. 它能够堆叠的非常深, 达到了64层, 其实它也是通过加深模型的方式来增长前文依赖能力的.

如果没有Transformer基础建议看我写过的<Transformer精讲>. 关于Vanilla Transformer, 其他具体内容如果想了解可以去看原论文.

在Transformer中通常需要设定一个固定的长度, 如果输入序列长小于固定长则进行填充. 因为使用字符级数据, 所以经常会出现大于序列长的情况. 它采用分段处理, 引入辅助函数训练.

与Transformer一样, 训练阶段, 模型能够一次处理整段数据:

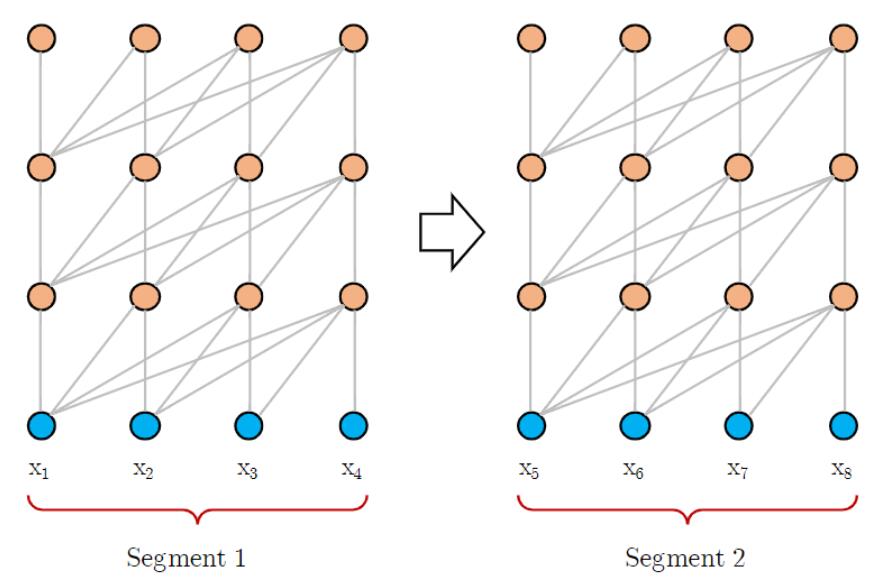
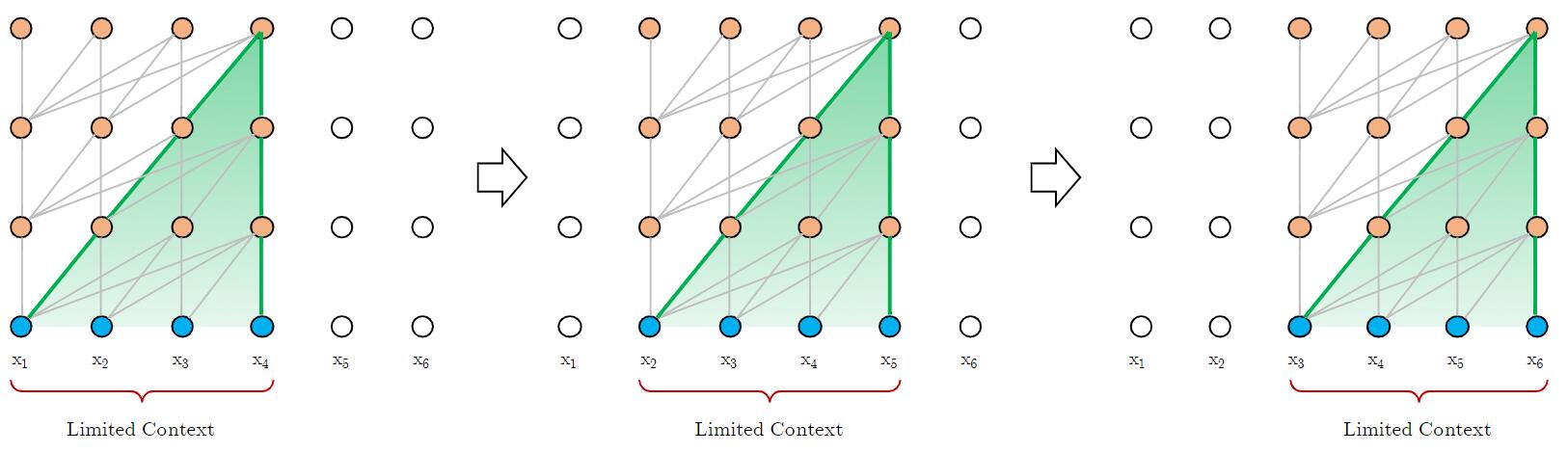
评估阶段, 模型需要按照自回归每次前进一个Token:

Transformer - XL

Transformer - XL出自论文Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context. 其中XL指的是extra - long. 作者主要通过Segment - Level Recurrence的方式来缓解Transformer中的内容长度限定问题, 其衍生问题由Relative Positional Encoding解决.

在Vanilla Transformer中的分段导致了两个问题:

1. 依赖的最大长度被固定长这个参数严格的限制了.
2. 在划分时很有可能会截断上下文的含义, 导致不同的Segment之间考虑不到上下文联系, 这被称为上下文碎片化(Context framentation).

不同段之间的梯度传播会被分段而截断:

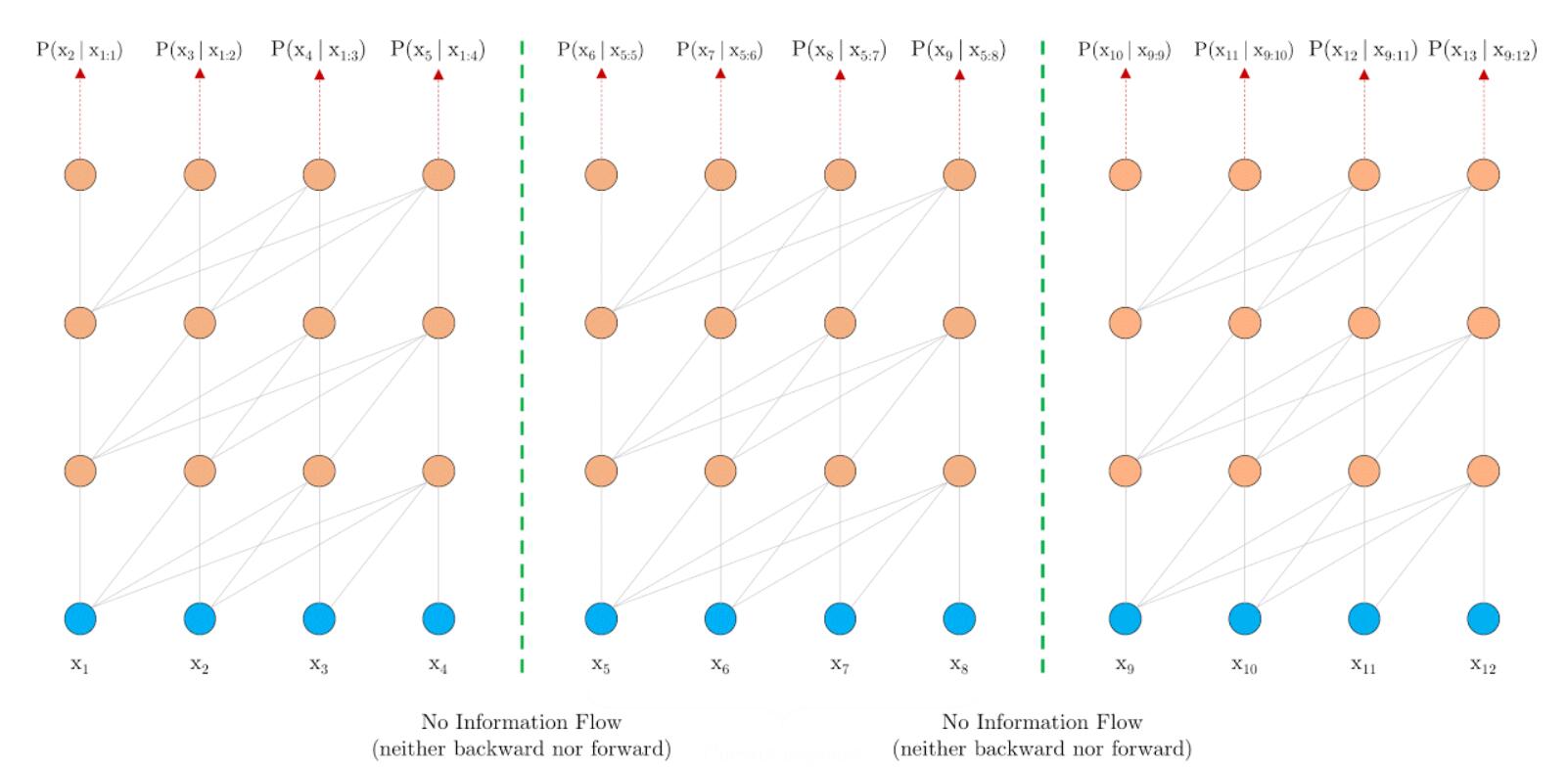
这两个缺陷是Transformer - XL改进的动机.

Segment - Level Recurrence with State Reuse

最首要的想法就是建立前后Segment之间的联系, 想办法将前面Segment的信息传到后面.

作者直接以Segment为单位进行操作, 每次都将同层上个Segment的隐态暂存下来, 而并非是对隐态重新计算. 但不保存梯度, 因为我们只是用同层的上个Segment隐态做为一种记忆信息对当前Segment产生影响, 并不需要进行反向传播. 储存的隐态数量尽可能多的.

$$
\begin{array}{l}
\widetilde{\mathbf{h}}_{\tau+1}^{n-1}=\left[\mathrm{SG}\left(\mathbf{h}_{\tau}^{n-1}\right) \circ \mathbf{h}_{\tau+1}^{n-1}\right] \\
\mathbf{q}_{\tau+1}^{n}, \mathbf{k}_{\tau+1}^{n}, \mathbf{v}_{\tau+1}^{n}=\mathbf{h}_{\tau+1}^{n-1} \mathbf{W}_{q}^{\top}, \widetilde{\mathbf{h}}_{\tau+1}^{n-1} \mathbf{W}_{k}^{\top}, \widetilde{\mathbf{h}}_{\tau+1}^{n-1} \mathbf{W}_{v}^{\top} \\
\mathbf{h}_{\tau+1}^{n}=\text { Transformer-Layer }\left(\mathbf{q}_{\tau+1}^{n}, \mathbf{k}_{\tau+1}^{n}, \mathbf{v}_{\tau+1}^{n}\right)
\end{array}
$$

其中$n$ 代表层数, $\tau$ 代表Segment号. $\mathrm{SG}(\cdot)$ 代表不求梯度, 不算作反向传播的一部分. 注意上面的式子, $\mathbf{k}_{\tau+1}^{n}$ 和 $\mathbf{v}_{\tau+1}^{n}$ 都是由当前Segment隐态和上个Segment隐态Concat后的$\widetilde{\mathbf{h}}_{\tau+1}^{n-1}$ 生成的, 而$\mathbf{q}_{\tau+1}^{n}$ 仅由当前Segment隐态$\mathbf{h}_{\tau+1}^{n-1}$影响. 每个Segment都做相同的动作, 因此称该方法为Segment - Level Recurrence.

在训练时仍然每次前进一段:

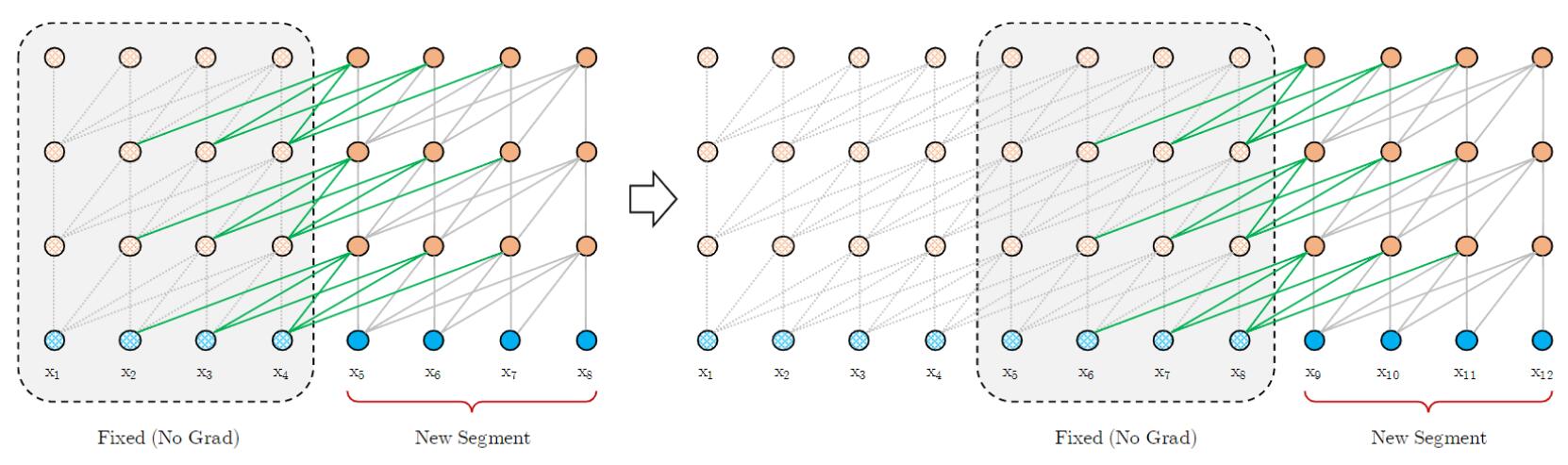
与Vanilla Transformer不同的是, 因为能够直接复用整个Segment的信息, 能够极大加快Evaluation的速度, 所以每次前进Segment个Token:

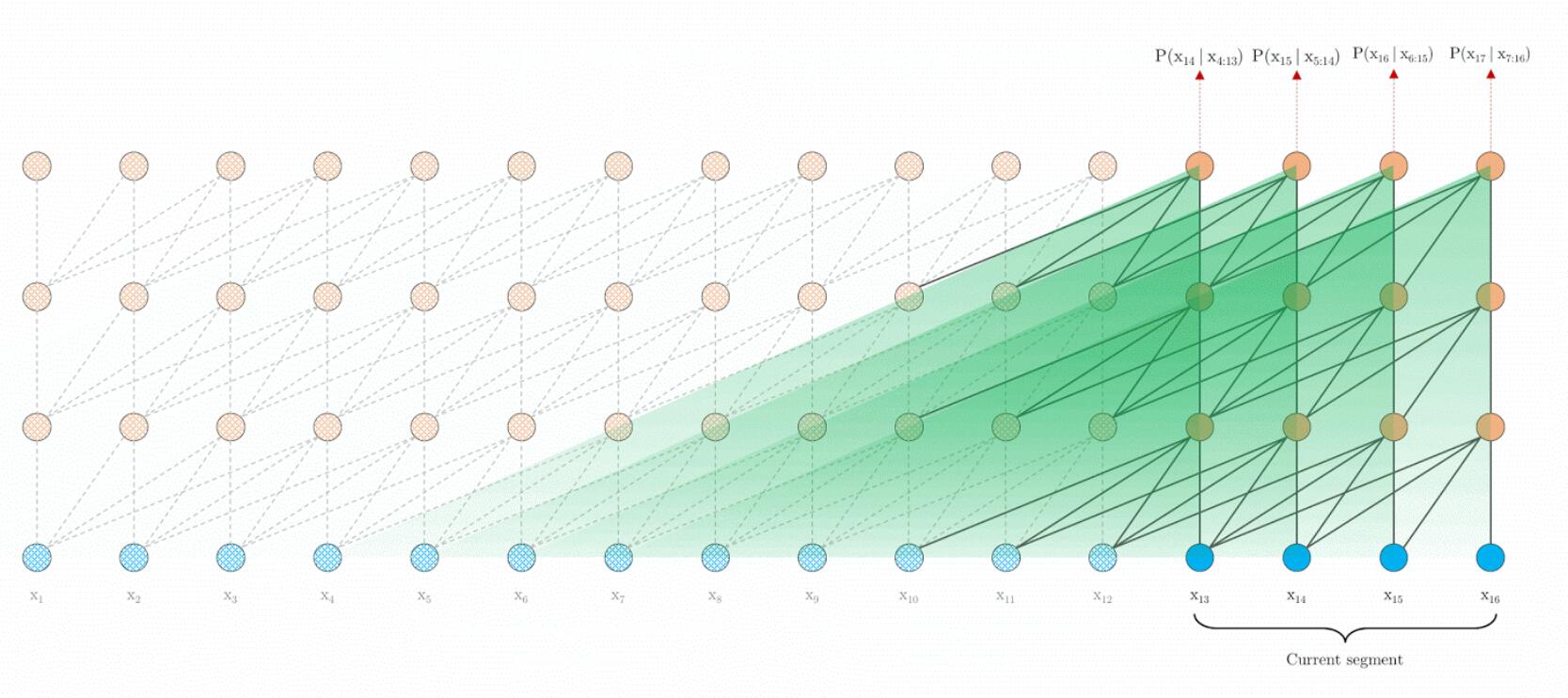
如果对前进Segment个Token有些模糊, 还是要理解作者是以整个Segment为单位进行操作的, 即使是进行自回归运算, 也是直接生成Segment个输出, 并输入进下个Segment.
$$
\mathbf{h}_{\tau}=f\left(\mathbf{h}_{\tau-1}, \mathbf{E}_{\mathbf{s}_{\tau}}+\mathbf{U}_{1: L}\right)
$$
如果在对前一个Segment的隐态和当前时刻隐态做Concat这个操作有疑惑, 我们来分析一下在这个计算过程中维度的变化. 请记住一个结论: Transformer隐态输出大小取决于Query的序列长度.

假设前一时刻隐态$\mathbf{h}_{\tau}^{n-1}$ 和当前时刻隐态$\mathbf{h}_{\tau+1}^{n-1}$ 的Size为$L\times d$, $W_q^T$, $W_v^T$, $W_k^T$ 的Size为$d_k \times d$. 在做完Concat后, 拼接后隐态$\widetilde{\mathbf{h}}_{\tau+1}^{n-1}$ Size为$2L \times d$, 看一下Attention分数的计算:
$$
\displaylines{
\mathbf{q}_{\tau+1}^{n}, \mathbf{k}_{\tau+1}^{n}, \mathbf{v}_{\tau+1}^{n}=\mathbf{h}_{\tau+1}^{n-1} \mathbf{W}_{q}^{\top}, \widetilde{\mathbf{h}}_{\tau+1}^{n-1} \mathbf{W}_{k}^{\top}, \widetilde{\mathbf{h}}_{\tau+1}^{n-1} \mathbf{W}_{v}^{\top} \\
\text{Attention Score}_{\tau+1}^n = \frac{\mathbf{q}_{\tau+1}^{n}{\mathbf{k}_{\tau+1}^{n}}^T}{\sqrt{d_k}}\mathbf{v}_{\tau+1}^{n}
}
$$
重复一遍之前的话, $\mathbf{k}_{\tau+1}^{n}$ 和 $\mathbf{v}_{\tau+1}^{n}$ 都是由当前Segment隐态和上个Segment隐态Concat后的$\widetilde{\mathbf{h}}_{\tau+1}^{n-1}$ 生成的, 而$\mathbf{q}_{\tau+1}^{n}$ 仅由当前Segment隐态$\mathbf{h}_{\tau+1}^{n-1}$影响.

在求得分时, $\mathbf{q}_{\tau+1}^{n}$ 的维度是$L \times d_k$, $\mathbf{k}_{\tau+1}^{n}$ 和的$\mathbf{v}_{\tau+1}^{n}$维度都是$2L \times d$, 求完$\mathbf{q}_{\tau+1}^{n} \cdot {\mathbf{k}_{\tau+1}^{n}}^T$ 后维度是$L\times 2L$, 然后与$\mathbf{v}_{\tau+1}^{n}$ 再相乘, 维度变成$L\times d_k$. 乘完后的计算维度是与Transformer保持一致的.

并且还能更好的联系前文信息, 每次能够依赖的最大长度也从$\text{Segment Length}$ 提升到$\text{Layer} \times \text{Segment Length}$的倍数:

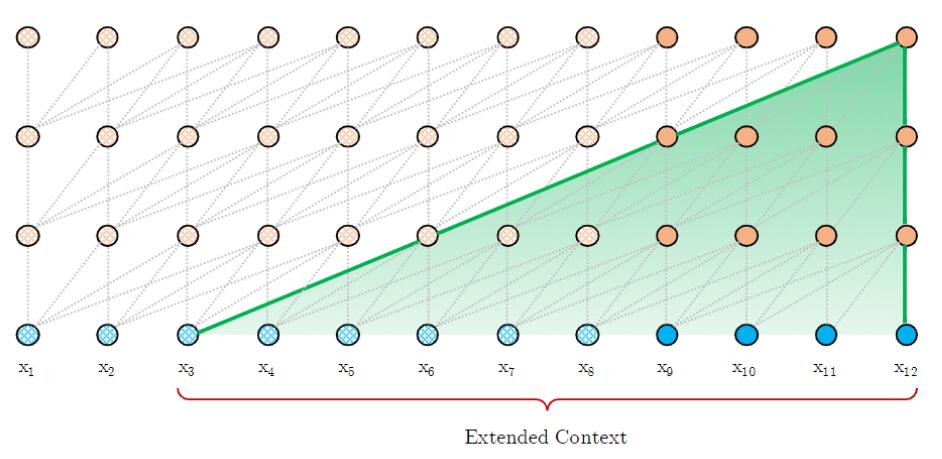
Relative Positional Encoding

虽然已经利用Segment - Level Recurrence来解决固定长问题, 但在计算位置编码时候还没有彻底将段递归的思想融合进去.

Absolute Positional Encoding

在Transformer中, 使用的是绝对位置编码:

$$
\begin{aligned}
\mathbf{A}_{i, j}^{\mathrm{abs}}&= \left[ \mathbf{W}_{q}\left( \mathbf{E}_{x_{i}}+\mathbf{U}_i \right)\right]^{\top} \mathbf{W}_{k}\left(\mathbf{E}_{x_j}+\mathbf{U}_j\right)\\
&=\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{E}_{x_{j}}}_{(a)}+\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{U}_{j}}_{(b)}
+\underbrace{\mathbf{U}_{i}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{E}_{x_{j}}}_{(c)}+\underbrace{\mathbf{U}_{i}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{U}_{j}}_{(d)}
\end{aligned}
$$

这个式子是由Transformer中的Attention拆来的, 其中$\mathbf{W}$ 代表权重矩阵, $\mathbf{E}$ 代表某个Token的Embedding, $\mathbf{U}$ 代表位置编码.

这样的位置编码在同一个Segment中是生效的, 但是对于不同的Segment就无法区分两个Segment中的同一对应位置, 即绝对位置不同, 但位置编码相同. 因此作者提出使用相对位置编码来解决该问题.

Relative Positional Encoding

作者先是说明了位置编码的作用:

Conceptually, the positional encoding gives the model a temporal clue or “bias“ about how information should be gathered.

概念上来说位置编码告诉模型一些如何收集信息的时序线索或者”偏置”.

when a query vector $q_{τ,i}$ attends on the key vectors $k_{τ,≤i}$, it does not need to know the absolute position of each key vector to identify the temporal order of the segment. Instead, it suffices to know the relative distance between each key vector $k_{τ,j}$ and itself $q_{τ,i}$, i.e. $i−j$.

但是在进行查询的时候, 每个key的绝对位置实际上通常是无关紧要的, 但与query的相对位置却非常关键. 也就是说我只要知道Query和Key的距离就足够了, 根本不关心它们到底处于原文中的哪个具体位置. 所以可以引入相对位置编码来告诉模型Token之间的相对位置关系, 从而代替更为复杂的绝对位置编码.

$$
\mathbf{A}_{i, j}^{\mathrm{rel}} =\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k, E} \mathbf{E}_{x_{j}}}_{(a)}+\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k, R} \mathbf{R}_{i-j}}_{(b)}
+\underbrace{u^{\top} \mathbf{W}_{k, E} \mathbf{E}_{x_{j}}}_{(c)}+\underbrace{v^{\top} \mathbf{W}_{k, R} \mathbf{R}_{i-j}}_{(d)}
$$

主要关注两个替换点:

• 所有与Key对应的绝对位置$j$ 相关的项$\mathbf{U}_j$ 应该被替换为相对位置项$\mathbf{R}_{i-j}$.
• 由于Query总出于同一位置, 所有与Query对应的绝对位置$i$ 相关的项$\mathbf{U}_i^{\top}\mathbf{W}_q^{\top}$ 也应该被替换掉, 在这里替换成两个可训练参数$u$ 和$v$ .

其中$\mathbf{R}_{i-j}$的编码方式与Transformer中的正余弦位置编码方式相同.

对于相对位置的四项, 作者做了汇总, 并给它们下了直观含义:

term (a) represents contentbased addressing, term (b) captures a contentdependent positional bias, term (c) governs a global content bias, and (d) encodes a global positional bias.

项数	绝对位置表示	相对位置表示	相对位置含义
a	$\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{E}_{x_{j}}$	$\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k, E} \mathbf{E}_{x_{j}}$	基于内容的寻址
b	$\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{U}_{j}$	$\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k, R} \mathbf{R}_{i-j}$	依赖内容的位置偏置
c	$\mathbf{U}_{i}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{E}_{x_{j}}$	$u^{\top} \mathbf{W}_{k, E} \mathbf{E}_{x_{j}}$	全局内容偏置
d	$\mathbf{U}_{i}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{U}_{j}$	$v^{\top} \mathbf{W}_{k, R} \mathbf{R}_{i-j}$	全局位置偏置

我开始很难理解(c)和(d)的含义到底是如何观察出来的. 如果从映射和查询的角度去理解的话, 可以看作是权重矩阵左侧的内容做了一次Embedding, 投影进潜在空间, 然后与权重矩阵右侧的内容计算得分.

个人理解还是有些模糊, 可解释性不够好.

在加上相对位置编码后, 整个过程就完善了, 形成一个闭环:
$$
\begin{aligned}
\widetilde{\mathbf{h}}_{\tau}^{n-1}=&\left[\mathrm{SG}\left(\mathbf{m}_{\tau}^{n-1}\right) \circ \mathbf{h}_{\tau}^{n-1}\right] \\
\mathbf{q}_{\tau}^{n}, \mathbf{k}_{\tau}^{n}, \mathbf{v}_{\tau}^{n}=& \mathbf{h}_{\tau}^{n-1} \mathbf{W}_{q}^{n \top}, \widetilde{\mathbf{h}}_{\tau}^{n-1} \mathbf{W}_{k, E}^{n}, \widetilde{\mathbf{h}}_{\tau}^{n-1} \mathbf{W}_{v}^{n \top} \\
\mathbf{A}_{\tau, i, j}^{n}=& \mathbf{q}_{\tau, i}^{\top} \mathbf{k}_{\tau, j}^{n}+\mathbf{q}_{\tau, i}^{n} \mathbf{W}_{k, R}^{n} \mathbf{R}_{i-j}
+u^{\top} \mathbf{k}_{\tau, j}+v^{\top} \mathbf{W}_{k, R}^{n} \mathbf{R}_{i-j} \\
\mathbf{a}_{\tau}^{n}=& \text { Masked-Softmax }\left(\mathbf{A}_{\tau}^{n}\right) \mathbf{v}_{\tau}^{n} \\
\mathbf{o}_{\tau}^{n}=& \text { LayerNorm }\left(\operatorname{Linear}\left(\mathbf{a}_{\tau}^{n}\right)+\mathbf{h}_{\tau}^{n-1}\right) \\
\mathbf{h}_{\tau}^{n}=& \text { Positionwise-Feed-Forward }\left(\mathbf{o}_{\tau}^{n}\right)
\end{aligned}
$$
其中$\mathbf{m}_{\tau}^{n-1}$ 指的是第$\tau$ 个Segment时GPU缓存中的所有第$n-1$ 层的隐态.

推荐阅读:

• Transformer-XL: Unleashing the Potential of Attention Models 是谷歌官方发布的Blog, 里面有动图.

XLNet

XLNet出自论文XLNet: Generalized Autoregressive Pretraining for Language Understanding.

虽然BERT在各类任务上的出色表现, 但BERT是一个自编码(Auto Encoding)模型, 相较与自回归(Auto Regressive)模型, 自编码模型在面对生成式的任务是天生具有劣势的(我们后面再提). XLNet尝试在自回归的基础上将BERT身上的优点吸取过来.

但是怎么才能在自回归模型中引入双向捕捉上下文的能力呢? 在先前的任务中, AR模型一般只能通过Forward和Backward两次单向编码来尝试捕捉上下文, 但并没有双向捕捉上下文效果来的理想, 下游任务又非常需要这种双向建模的能力. 自回归和自编码的模型各有优劣, 很多时候特点既是一种优势, 也是一种限制. AR模型受限于自身结构, 不能从结构上改变. 作者巧妙的想到了利用打乱Token之间的顺序来获取上下文.

Why not BERT?

Disadvantage of BERT

XLNet的作者指出了BERT的两个致命缺点:

1. 被BERT使用的人工制造符号譬如[MASK]完全贯穿于BERT的预训练过程, 但在用实际数据做Fine - tune时根本没有, 导致了预训练和微调之间的差异. 我记得在BERT中, 作者提到了缓解这个问题的方案, 但不能从根本上解决这个问题:

   在Fine tune的时候不可能对单词进行Mask, 这样就会导致预训练和微调的不匹配, 为缓解这种问题, 并非总是将选中的单词Mask, 而是在每个句子中, 有15%的词会被选中, 在选中单词后有三种可能性:

   1. 80%的概率将被选中的单词替换为[MASK].
   2. 10%的概率将被选中的单词替换为随机词.
   3. 10%的概率对被选中的单词不进行替换.

2. BERT假设被Mask掉的Token与句子中剩下的内容是独立的, 但在实际任务中普遍有远程依赖.

   比如”New York is a city.” 假设Mask了”New”和”York”两个词语, 那么在已知”is a city”的情况下, 就不太可能预测准确.

Comparsion of AutoEncoding and AutoRegressive

假设你真的不知道AE和AR是什么意思, 我们用大白话给AE何AR重新下个定义吧:

• 自回归模型(AR): 将上一时刻的输出作为输入, 对当前时刻输出进行预测.

  

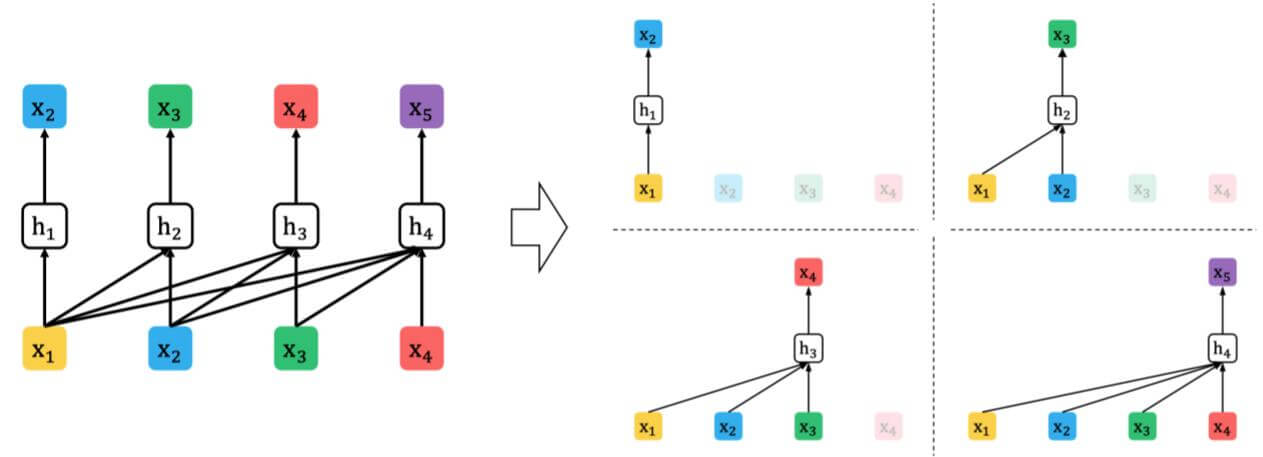
• 自编码模型(AE): 把完整的内容破坏掉一部分作为输入, 来预测被破坏掉的那部分.

  

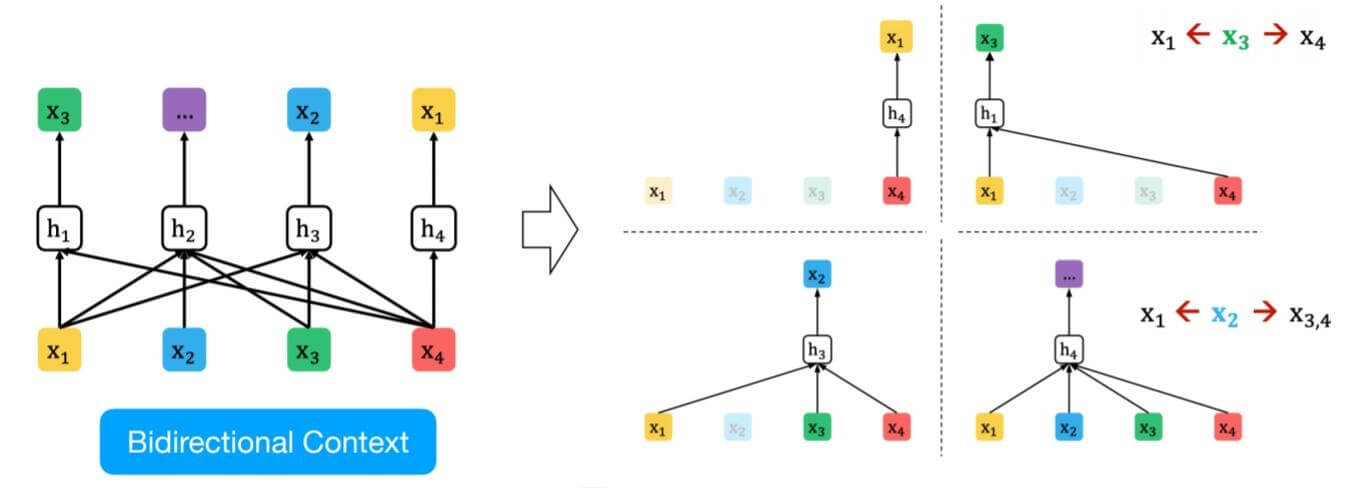
上述图片出自NLPCC 2020中科大讯飞和HIT - SCIR做的报告<Revisiting Pre-Trained Models for Natural Language Processing>.

对给定的文本输入序列$\mathbf{x}=\left[x_{1}, \cdots, x_{T}\right]$, $e(x)$ 代表Token $x$ 的Embedding.

自回归模型的任务目标是最大似然该函数:
$$
\max _{\theta}\quad \log p_{\theta}(\mathbf{x})=\sum_{t=1}^{T} \log p_{\theta}\left(x_{t} \mid \mathbf{x}_{<t}\right)=\sum_{t=1}^{T} \log \frac{\exp \left(h_{\theta}\left(\mathbf{x}_{1: t-1}\right)^{\top} e\left(x_{t}\right)\right)}{\sum_{x^{\prime}} \exp \left(h_{\theta}\left(\mathbf{x}_{1: t-1}\right)^{\top} e\left(x^{\prime}\right)\right)}
$$
但是对于AE模型来说(主要以BERT作为对比对象), 由于会选中15%的Token做Mask, 假设被污染的Token用$\hat{\mathbf{x}}$ 表示, 自编码模型的任务目标是从带噪声的$\hat{\mathbf{x}}$ 中重建$\overline{\mathbf{x}}$:
$$
\max _{\theta}\quad \log p_{\theta}(\overline{\mathbf{x}} \mid \hat{\mathbf{x}}) \approx \sum_{t=1}^{T} m_{t} \log p_{\theta}\left(x_{t} \mid \hat{\mathbf{x}}\right)=\sum_{t=1}^{T} m_{t} \log \frac{\exp \left(H_{\theta}(\hat{\mathbf{x}})_{t}^{\top} e\left(x_{t}\right)\right)}{\sum_{x^{\prime}} \exp \left(H_{\theta}(\hat{\mathbf{x}})_{t}^{\top} e\left(x^{\prime}\right)\right)}
$$

其中当Token $x_t$ 被Mask时$m_t=1$, 其他时候为0. $H_\theta$ 是Transformer将长度为$T$ 的文本序列$\mathbf{x} $ 映射成隐态向量$H_{\theta}(\mathbf{x})=\left[H_{\theta}(\mathbf{x})_{1}, H_{\theta}(\mathbf{x})_{2}, \cdots, H_{\theta}(\mathbf{x})_{T}\right]$ .

注意这两个目标函数, 首先条件不同, 其次是隐态表示不同. AR模型中因为只能看到前文的信息, 而AE模型能够看到全部的上下文信息. 将二者比较后, 作者得出三个结论:

• 独立假设: 这里强调了在自编码任务目标中的$\approx$, BERT假设在给定$\hat{\mathbf{x}}$ 的情况下被Mask的词是相互独立的. 而AR模型不需要独立性假设.

• 输入噪声: 在预训练时会出现特殊的人造Token, Fine - tune时没有, 导致不匹配. 而AR模型不对输入引入噪声, 所以不会遇到该问题.

• 上下文依赖: AR模型只能捕捉到位置位于前面的信息$h_\theta(\mathbf{x_{1:t-1}})$, BERT能更好的捕捉双向上下文信息$H_\theta(\mathbf{x})_t$.

  对于双向捕捉可以参考ELMo, GPT, BERT.

作者观察到的这三点非常重要, 作为模型的改进方向.

此外, AR模型的特性能带来一个AE模型不能带来的优势, 这也是BERT为捕捉双向上下文付出的代价. 我们考虑一个场景:

• BERT要对[New, York, is, a, city] 中的[New, York] 进行预测, 作为AE模型对[New, York] 做了Mask.
• XLNet要对[is, a, city, New, York] 中的[New, York] 进行预测, 作为AR模型, 需要先预测出[New], 再利用[New] 的信息预测[York].

那么这两种方式产生的信息量是绝对不一样的:
$$
\begin{aligned}
\mathcal{J}_{\mathrm{BERT}} &=\log p(\text { New } \mid \text { is a city })+\log p(\text { York } \mid \text { is a city }) \\
\mathcal{J}_{\mathrm{XLNet}} &=\log p(\mathrm{New} \mid \text { is a city })+\log p(\text { York } \mid \mathrm{New}, \text { is a city })
\end{aligned}
$$
很明显, XLNet因为是AR模型, 永远都能学到更多的依赖对. 至于为什么可以在二者输入不一样的情况下进行比较, 在读完下一小节后你就会恍然大悟.

在附录中还有更多的比对, 更详细的内容请自行阅读原论文.

Permutation Language Model Based on AutoRegressive Model

由于AR语言模型比较特殊, 不好实现像BERT那样双向捕捉上下文的效果. 作者提出用置换的方法, 既能保留AR模型的优势, 又允许模型捕捉上下文.

对于给定长度为$T$ 的序列$\mathbf{x}$, 总共有$T!$ 种不同的排列方式. 如果模型参数能通过多次随机的句子排列共享, 那么AR模型就能将所有位置上的信息结合到一起.

假设$\mathcal{Z}_{T}$ 代表长度为$T$ 的序列下标, $z_t$ 代表第$t$ 个元素, $\mathbf{z}_{<t}$ 代表置换后的前$t-1$ 个元素.

沿着之前AR模型的目标, 现在给置换语言模型(PLM)的基本优化目标重新下个定义吧:
$$
\max _{\theta} \mathbb{E}_{\mathbf{z} \sim \mathcal{Z}_{T}}\left[\sum_{t=1}^{T} \log p_{\theta}\left(x_{z_{t}} \mid \mathbf{x}_{\mathbf{z}<t}\right)\right]
$$
我们的目标只是单纯的从原来有序的输入序列变成了位置随机重排后的序列, 这样在做自回归时就能够看到原本不属于该位置的元素, 这样就能双向捕捉上下文.

作者在这里强调, 仅生成一个置换后的新下标序列, 而输入序列的原文顺序是不变的. 沿用与原始输入相对应的位置编码, 并依靠Attention来实现对下标的置换. 因为在FineTuning期间文本的顺序是正常而不发生置换的.

作者给出了一张对置换部分的阐述图, 假设当前要对$x_3$ 进行预测, 在置换语言模型中只能通过Attention来关注置换后序列在$3$ 前的输入:

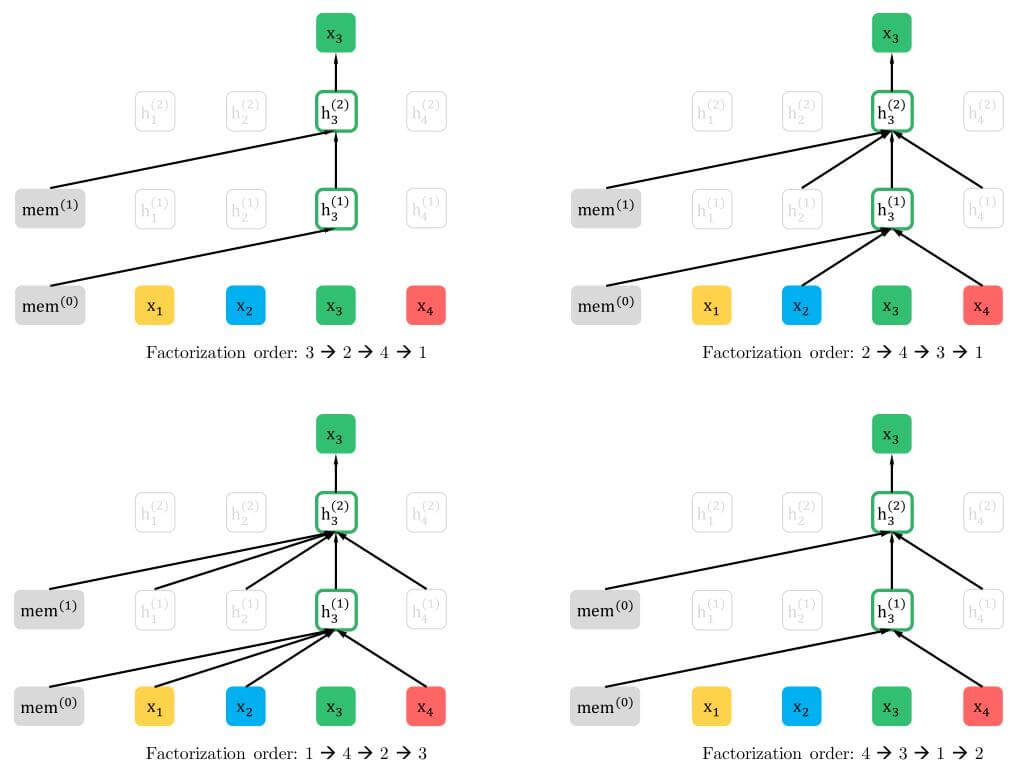
例如左上角, 分解顺序为$3 \rightarrow 2 \rightarrow 4 \rightarrow 1$ 时, 只能对之前的隐态$\text{mem}$ 做Attention. 右上角, 分解顺序为$2 \rightarrow 4 \rightarrow 3 \rightarrow 1$ 时, 只能对置换顺序在$3$ 前的$2$ 和 $4$ 做Attention. 下面两幅图同理.

是不是有些巧妙? 对, 置换的方法确实比较巧妙, 但是请思考一个问题, 假设置换后的顺序为$2 \rightarrow 4 \rightarrow 3 \rightarrow 1$, 马上就要预测$x_3$ 了, 由于打乱了顺序, 模型怎才能知道它要预测的是$x_3$ 还是 $x_1$ 呢?

Two - Stream Self - Attention for Target - Aware Representations

Target - Aware

由于采用了置换的方式, 所以按照Transformer的方法处理目标可能会遇到一些问题.

如果我们沿用之前Transformer的方式, $h_{\theta}\left(\mathbf{x}_{\mathbf{z}<t}\right)$ 代表$\mathbf{X}_{\mathbf{Z}<t}$ 的隐态, 来计算下一个单词的分布:
$$
p_{\theta}\left(X_{z_{t}}=\right.\left.x \mid \mathbf{x}_{\mathbf{z}<t}\right)=\frac{\exp \left(e(x)^{\top} h_{\theta}\left(\mathbf{x}_{\mathbf{z}<t}\right)\right)}{\sum_{x^{\prime}} \exp \left(e\left(x^{\prime}\right)^{\top} h_{\theta}\left(\mathbf{x}_{\mathbf{z}<t}\right)\right)}
$$
由于我们之前打乱了原有的句子顺序, 模型完全不知道该预测哪个Token了. 对于未知的所有Token, 它们有可能不在原来的位置上, 也有可能在原来的位置上. 换句话说, 如果使用Transformer的方法, 下一个要预测的Token分布与它原来的位置就没有关联了.

因此必须将下一个要预测的Token通过某种方式显式的告诉模型, “哦它才是打乱顺序后我该预测的下一个Token”, 这也就是论文中说的Target - Aware:
$$
p_{\theta}\left(X_{z_{t}}=x \mid \mathbf{x}_{z<t}\right)=\frac{\exp \left(e(x)^{\top} g_{\theta}\left(\mathbf{x}_{\mathbf{z}<t}, z_{t}\right)\right)}{\sum_{x^{\prime}} \exp \left(e\left(x^{\prime}\right)^{\top} g_{\theta}\left(\mathbf{x}_{\mathbf{z}<t}, z_{t}\right)\right)}
$$
$g_{\theta}\left(\mathbf{x}_{\mathbf{z}<t}, z_{t}\right)$ 代表加入目标位置信息的表示方法.

Two - Stream Self - Attention

因为置换把要预测的Token的位置信息直接搞掉了, 所以必须通过其他方式提供位置信息. 我们必须符合以下两个点的限制:

1. 预测$x_{z_t}$ 时, $g_{\theta}\left(\mathbf{x}_{\mathbf{z}<t}, z_t\right) $ 不能$z_t$ 处的内容信息$x_{z_t}$, 只能使用$z_t$ 处的位置信息.
2. 在预测一个位置上$j>t$ 的Token$x_{z_j}$ 时, $g_{\theta}\left(\mathbf{x}_{\mathbf{z}<t}, z_t\right) $ 应该将$x_{z_t}$ 编码来提供全部的上下文信息.

基于这两点规则, XLNet采用双流注意力机制, 其中一种注意力提供上下文信息, 另一种提供位置信息.

• $h_\theta\left(\mathbf{x}_{\mathbf{z}\leq t}\right)$, 记为$h_{z_t}$, 表示包括$x_{z_t}$ 在内的编码的上下文信息, 与标准的Transformer相同, 被称作为内容流(Content Stream).
• $g_\theta\left(\mathbf{x}_{\mathbf{z}_<t}, z_t\right)$, 记为$g_{z_t}$, 表示仅包括$\mathbf{x}_{\mathbf{z} < t}$ 在内的上下文信息和$z_t$ 的位置信息, 并没有$x_{z_t}$ 处的位置信息, 被称之为请求流(Query Stream).

Content Stream and Query Stream

下面就来以论文中的图为例子, 看一下具体的双流注意力在场景中的结构.

第一层的Query Stream被定义为一个可训练的向量, 记作$g_i^{(0)}=w$, 设置Content Stream是对应的Embedding, 记作$h_i^{(0)}=e(x_i)$. Self - Attention层记为$m=1,\dots,M$.

XLNet的每一层与Transformer - XL相同, 包括FFN, Layer Norm, 残差连接, 多头注意力… 这些细节都暂时省略掉, 到后面我们会串起来看.

先来看看最熟悉的Self - Attention, 这与Transformer中是保持一致的, 不要忘记它也被称为内容流:

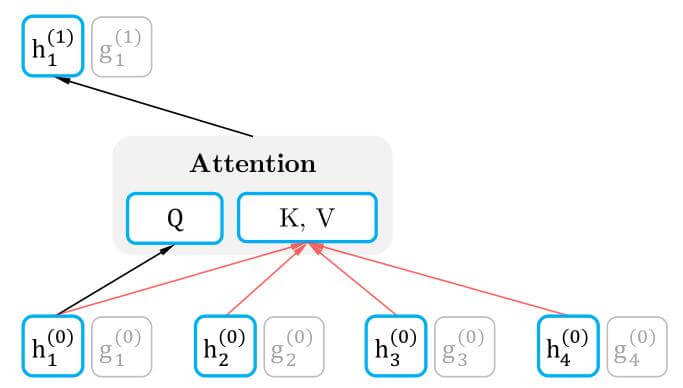
Content Stream能使用包括其本身在内的所有上下文信息. 为了存储上下文信息, 所以Q依赖于上层对应位置的Content Stream, K和V均依赖于所有输入的隐态:
$$
h_{z_{t}}^{(m)} \leftarrow \text { Attention }\left(\mathrm{Q}=h_{z_{t}}^{(m-1)}, \mathrm{KV}=\mathbf{h}_{\mathrm{z} \leq t}^{(m-1)} ; \theta\right), \quad\left(\text {content stream: use both } z_{t} \text { and } x_{z_{t}}\right)
$$
下面来看看XLNet中独有的请求流$g_\theta$:

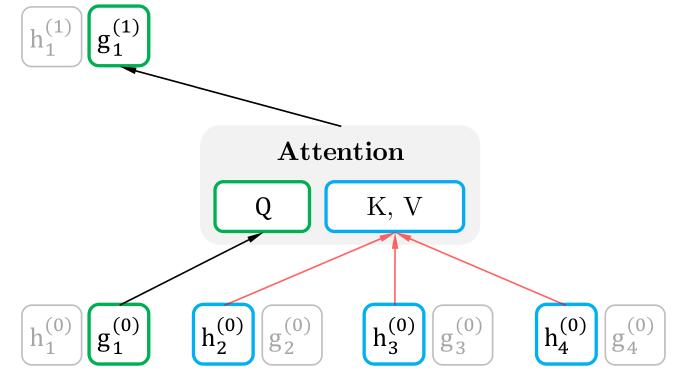
因为只用于发起请求, 请求流的Q只能由上一层的Query Stream生成, 而K和V不能使用当前位置的内容信息, 所以只能由其他位置的上下文信息决定:
$$
g_{z_{t}}^{(m)} \leftarrow \text { Attention }\left(\mathrm{Q}=g_{z_{t}}^{(m-1)}, \mathrm{KV}=\mathbf{h}_{\mathrm{z}<t}^{(m-1)} ; \theta\right), \quad \text { (query stream: use } z_{t} \text { but cannot see } \left.x_{z_{t}}\right)
$$
对比一下Query Stream和Content Stream, 二者的不同点主要在Q的依赖来源和能否使用上层当前位置的内容信息 $h_{z=t}^{(m-1)}$:
$$
\begin{aligned}
&g_{z_{t}}^{(m)} \leftarrow \text { Attention }\left(\mathrm{Q}=g_{z_{t}}^{(m-1)}, \mathrm{KV}=\mathbf{h}_{\mathrm{z}<t}^{(m-1)} ; \theta\right), \quad \text { (query stream: use } z_{t} \text { but cannot see } \left.x_{z_{t}}\right)\\
&h_{z_{t}}^{(m)} \leftarrow \text { Attention }\left(\mathrm{Q}=h_{z_{t}}^{(m-1)}, \mathrm{KV}=\mathbf{h}_{\mathrm{z}<t}^{(m-1)} ; \theta\right), \quad\left(\text {content stream: use both } z_{t} \text { and } x_{z_{t}}\right)
\end{aligned}
$$

Permutation Attention Mask

其实我们也不用做真正意义上的置换, 只需要将Attention中的Mask机制结合起来使用就好, 如下图:

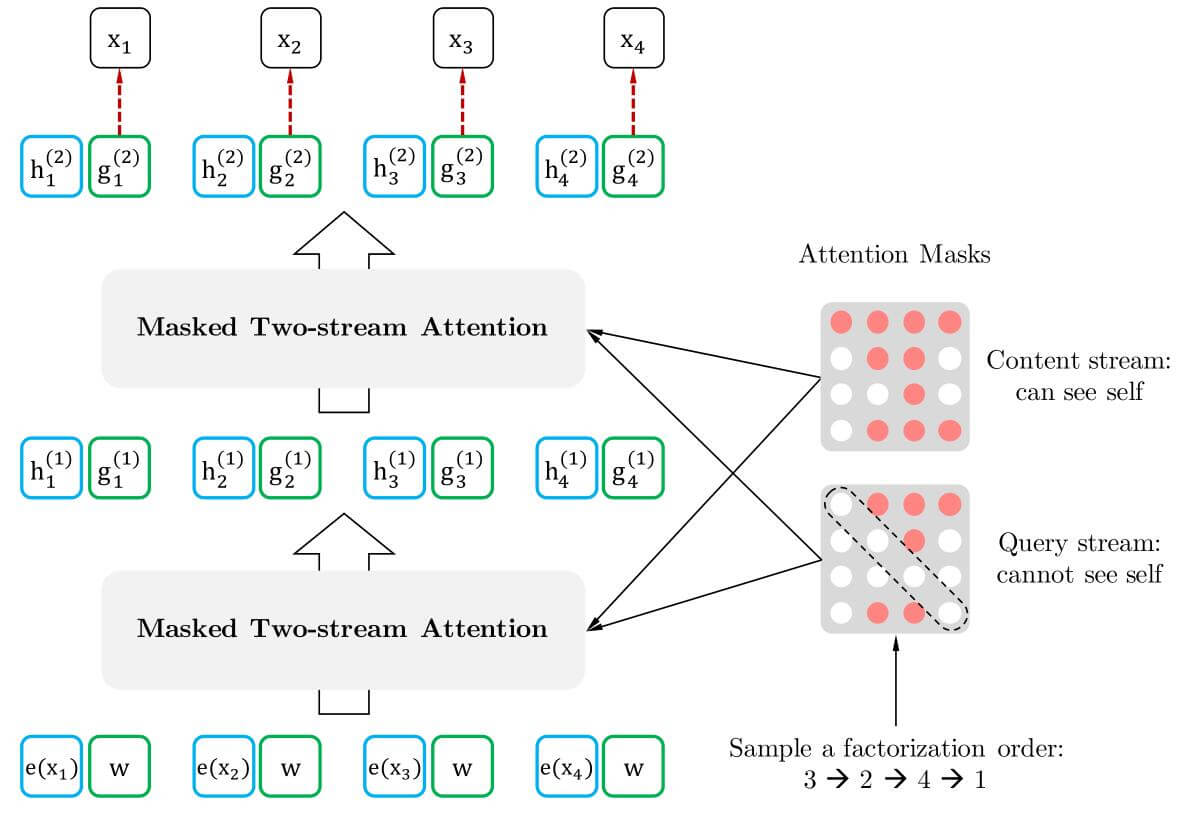
图中的白点代表被Mask, 红点代表可以被Attend.

置换后的顺序为$3\rightarrow2\rightarrow4\rightarrow1$ 时, 请求流是不能看到当前正在预测的Token的内容信息的, 所以请求流矩阵主对角线一定都是被Mask的. 因为第一个要预测的就是位置$3$ 的内容, 所以矩阵第三行全都被Mask. 在预测出位置$3$ 后的内容后, 在请求流矩阵第二行的第三列就变得已知了. 在预测位置$4$ 和$1$ 时同理.

当搞懂了请求流矩阵后, 再看内容流矩阵, 完全符合我们之前对这两种流的定义: 内容流矩阵不过是请求流矩阵主对角线没被Mask而已, 因为请求流的要求是当前要预测的内容不可知, 内容流却只是存储上下文, 没有这种限制.

Particial Prediction

在实验过程中, 发现如果对所有置换后的序列输入进行预测, 会导致收敛缓慢, 难以优化. 作者只去预测置换后序列的最后几个Token, 这样置换后序列$\mathbf{z}$ 就被分成了两个部分, 分别是分割点$c$ 前的$\mathbf{z}_{\leq c}$, 和需要预测的分割点后的序列$\mathbf{z}_{>c}$. 根据这个变化, XLNet的优化目标变为:
$$
\max _{\theta} \mathbb{E}_{\mathbf{z} \sim \mathcal{Z}_{T}}\left[\log p_{\theta}\left(\mathbf{x}_{\mathbf{z}>c} \mid \mathbf{x}_{\mathbf{z} \leq c}\right)\right]=\mathbb{E}_{\mathbf{z} \sim \mathcal{Z}_{T}}\left[\sum_{t=c+1}^{|\mathbf{z}|} \log p_{\theta}\left(x_{z_{t}} \mid \mathbf{x}_{\mathbf{z}<t}\right)\right]
$$

关于分割点, 作者假设了超参数$K$, 设$|\mathbf{z}| /(|\mathbf{z}|-c) \approx K$. 有$\frac{1}{K}$ 个Token需要被预测, 不需要预测的Token所对应的Query Stream是不需要被计算的, 这样能够节省计算资源.

Integrate Attention into Transformer Backbone

我们现在可以把除了双流Attention以外的结构加进来了, 仍然也都是Transformer中的组件, 只是位置编码采用的是相对位置编码(这里的相对位置编码和Transformer - XL还不一样, 后面会提及).

对于时间步$t=1,\dots,T$, 将含有相对位置编码的Attention记为$\text{RelAttn}$, 将Position - wise的Feed Forward记为$\text{PosFF}$, 整个双流Attention更新过程如下:
$$
\begin{array}{l}
\hat{h}_{z_{t}}^{(m)}=\text { LayerNorm }\left(h_{z_{t}}^{(m-1)}+\operatorname{RelAttn}\left(h_{z_{t}}^{(m-1)},\left[\tilde{\mathbf{h}}^{(m-1)}, \mathbf{h}^{(m-1)}_{\mathbf{z}_{\leq t}}\right]\right)\right) \\
h_{z_{t}}^{(m)}=\text { LayerNorm }\left(\hat{h}_{z_{t}}^{(m)}+\operatorname{PosFF}\left(\hat{h}_{z_{t}}^{(m)}\right)\right) \\
\hat{g}_{z_{t}}^{(m)}=\text { LayerNorm }\left(g_{z_{t}}^{(m-1)}+\operatorname{RelAttn}\left(g_{z_{t}}^{(m-1)},\left[\tilde{\mathbf{h}}^{(m-1)}, \mathbf{h}_{\mathbf{z}<t}^{(m-1)}\right]\right)\right) \\
g_{z_{t}}^{(m)}=\text { LayerNorm }\left(\hat{g}_{z_{t}}^{(m)}+\operatorname{PosFF}\left(\hat{g}_{z_{t}}^{(m)}\right)\right)
\end{array}
$$

Incorporating Ideas From Transformer - XL

因为Transformer - XL是最近颇有成效的AR模型, 所以作者尝试将它的两种最关键的技术相对编码和段级递归引入, 与XLNet结合. 作者引入了两种相对编码, Transformer - XL一模一样的相对位置编码和结合段问题添加的相对段编码.

Segement Level Recurrence

其实和Transformer - XL中的段级递归一样. 假设现在有两段长序列$\mathbf{s}$, $\tilde{\mathbf{x}}=\mathbf{s}_{1: T}$ 与 $\mathbf{x}=\mathbf{s}_{T+1: 2 T}$, 其置换后的序列分别是$\tilde{\mathbf{z}}=\text{Permutation}([1\cdots T])$ 和 $\mathbf{z}=\text{Permutation}([T+1\cdots 2T])$. 那么计算第二段$\mathbf{x}$的内容流可以按照如下方式更新:
$$
h_{z_{t}}^{(m)} \leftarrow \text { Attention }\left(\mathrm{Q}=h_{z_{t}}^{(m-1)}, \mathrm{KV}=\left[\tilde{\mathbf{h}}^{(m-1)}, \mathbf{h}_{\mathbf{z}_{\leq t}}^{(m-1)}\right] ; \theta\right)
$$
将Memory中缓存的隐态$\tilde{\mathbf{h}}^{(m-1)}$ 和$\mathbf{x}$ 产生的隐态$\mathbf{h}_{\mathbf{z}_{\leq t}}^{(m-1)}$ Concat起来, 一起计算K和V.

Multiple Segments

XLNet与BERT一样, 在预训练阶段也是随机选择了两段连续或不连续的上下文合并到一起, 作为一个序列的两个Segment输入进XLNet中, 但只对连续内容使用Segment Memory. 两段之间采用的符号也和BERT类似, [CLS, A, SEP, B, SEP].

Relative Segment Encoding

注意, 这是相对段编码而并非相对位置编码. XLNet中的段编码方式与BERT中的绝对段编码方式不同, XLNet采用相对段编码.

对于给定的序列位置$i$ 和 $j$, 当这两个位置都位于同一个Segment时, 令$s_{ij}=s_+$, 否则$s_{ij}=s_-$. 其中$s_+$ 和$s_-$ 是每个注意力头分别学习的. 这种编码只关注两个Token是否位于同个Segment内, 而并不考虑来自于哪个特定的Segment, 这个角度来看与相对编码的思想是保持一致的.

在计算注意力时, $i$ 对$j$ 的注意力是这样计算的:
$$
a_{i j}=\left(\mathbf{q}_{i}+\mathbf{b}\right)^{\top} \mathbf{s}_{i j}
$$
$q_i$ 是标准注意力计算来的Query Vector, $\mathbf{b}$ 是一个可学习的参数, 最后将这个注意力$a_{ij}$和正常的注意力相加得到最终的注意力.

相对编码增强了模型的泛化能力, 并提供了完成多段输入任务的可能性.

Summary

Transformer - XL结合了段循环和注意力机制, 缓解了Transformer受限于输入长度的问题, 也节省了计算资源的开销, 减少了不必要的计算. 并在段循环的基础上做出相对位置编码的改进.

XLNet用置换的方法将AE模型引以为傲的双向捕捉上下文能力移植到AR模型上, 将Transformer - XL的特性也组装到自己的模型中.

从大家对XLNet的看法来说, 它是饱受争议的. 虽然根据所给出的实验数据来说, XLNet能够取得比较好的效果, 但是对比BERT使用的13G数据, XLNet使用了158G数据, 而BERT才仅仅使用了13G数据, 到底是模型本身的方法导致效果好, 还是数据堆上去的, 我个人认为很难说. 后人基于XLNet所作出的后续研究非常少. 相反, BERT的魔改模型都快一窝了.

我记得前段时间还有人说XLNet完爆BERT, 大家吵得不可开交. 具体见XLNet团队：只要公平对比，BERT毫无还手之力(可能也有点标题党的嫌疑).

另外吐槽一下, 因为XLNet整篇论文特别碎, 也很乱, 所以才一直拖着, 毕竟写这篇博客实在是太费劲了. 虽然明确的指出了BERT确实存在的问题, 但XLNet解决方案不是很优雅, 感觉像一堆零件拼凑到了一起.

虽然XLNet诟病繁多, 但XLNet为AR模型实现双向上下文捕捉能力提供了可能, 这种带领大家突破BERT框架的思维模式还是很重要的..