发布日期: 2020-12-27

更新日期: 2022-03-27

文章字数: 4.5k

阅读时长: 16 分

Realistic Re-evaluation of Knowledge Graph Completion Methods: An Experimental Study

本文是论文Realistic Re-evaluation of Knowledge Graph Completion Methods: An Experimental Study 的阅读笔记和个人理解.

Basic Idea

作者发现, 在FB15k和WN18中存在着大量的逆关系和重复关系, 表现出高度冗余, 从而导致Data Leakage. 作者希望能够系统性的去评估这些存在问题所带来的危害. 这些数据集上含有问题的关系导致了KGE模型在Link Prediction上的表现被高估了.

例如, 前人已经发现逆关系在FB15k和WN18中大量出现, 在去除逆关系前后对模型性能的影响非常大:

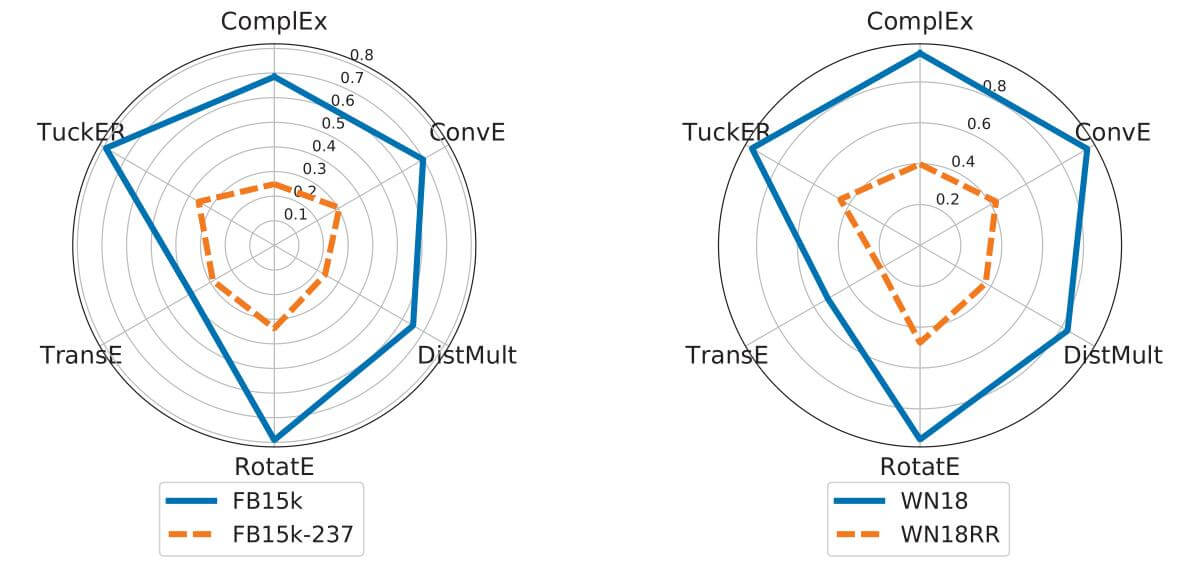
Evaluation Framework

本节是对目前现存的KGE中评估框架的简单的介绍, 为后文作者所进行的所有实验做简单的铺垫, 对于一些KGE领域的常识在此不再赘述, 详细内容请读者自行查阅.

Evaluation DataSets

现在KGE评估所使用的主流数据集是FB15k, FB15k - 237, WN18, WN18RR. YAGO在最近的论文中似乎用的比较少. 数据集中的实体, 关系个数以及它们所使用的数据划分如下所示:

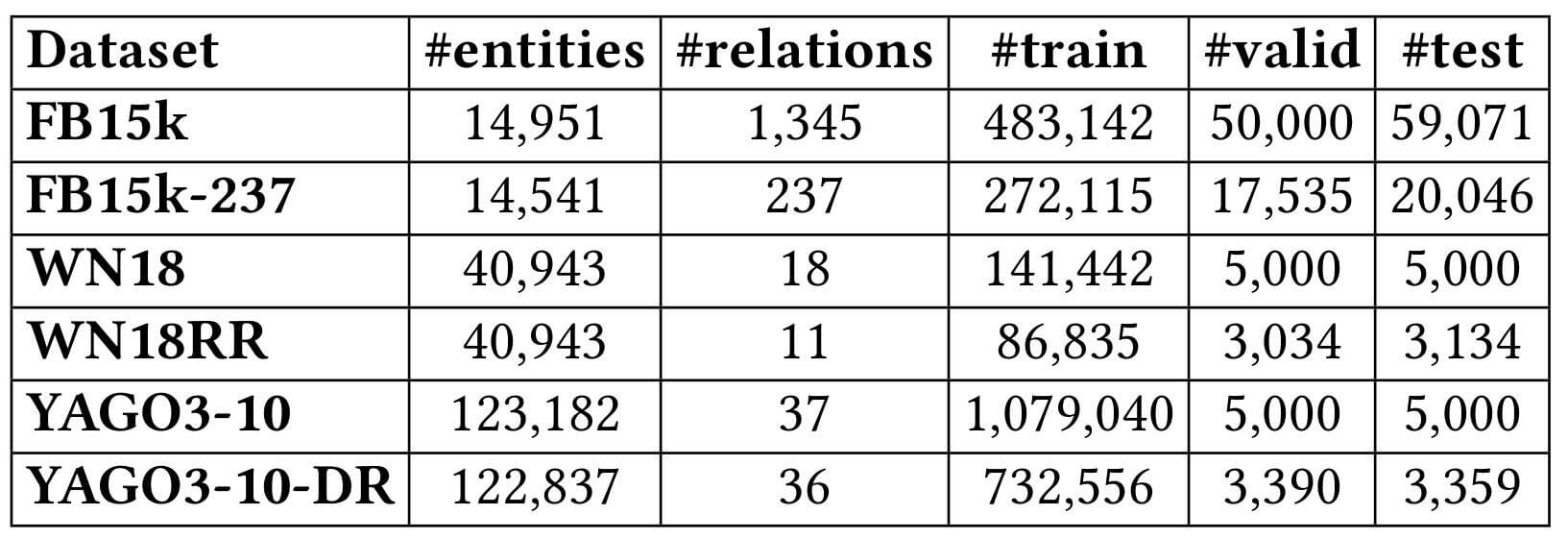
FB15k - 237, WN18RR, YAGO3 - 10 - DR是针对逆关系处理过后的数据集, 其实体或关系数据量都有不同程度的下降.

Evaluation Method and Measures

现在常用的评估指标主要和搜索问题上相关的评估指标相重合.

首先, 要明确KGE模型主要使用链接预测作为评估模型的主要任务. 即对于完整的三元组$(h, r, t)$, 在丢失头实体$h$ 或者尾实体$t$ 的情况下, 需要通过问题$(h, r, ?)$ 或$(?, r, t)$ 信息来预测出丢失的部分. 从这个角度来看, 将Link Prediction用于知识图谱补全, 本身与一个搜索问题无异.

在搜索问题中常用的指标如下:

指标名	正方向	描述
Hits@k	↑	概率最高的k个结果若正确则为命中
MR(Mean Rank)	↓	正确实体在所有实体中的排名, 并将它们相加求平均
MRR(Mean Reciprocal Rank)	↑	正确实体在所有实体中的排名的倒数, 并将它们相加求平均

当然, 由于可能存在多个正确的头实体或尾实体答案, 上述没有经过任何过滤的排名评估计算方式被称为Raw, 如果将其余正确的答案从测试集中去除, 仅保留唯一的正确答案, 则称为Filtered. 那么上述评估指标也被相应的替换为FHits@k(↑), FMR(↓), FMRR(↑), 方向保持不变.

该方法在TransE中被提出, 详见TransE.

Inadequacy of Benchmarks and Evaluation Measures

本文的核心工作在本节. 本节作者着重叙述了在FB15K和WN18中出现的种种问题. 主要存在的问题是逆关系和笛卡尔积关系. 逆关系其实已经被前人所提出并解决, 作者比较新颖的概念是提出了笛卡尔积关系.

Identifying the Most Probable Freebase Snapshot for Producing FB15k

为了探寻FB15k中各类缺陷的根本原因, 作者需要观察Freebase原本的样貌. 但Freebase是一直在进行更新的, FB15k并未声明是在哪个时间节点进行创建. Freebase可能会由类似于快照的形式存储起来, 过一段周期对Freebase保存一次, 作者尝试搜索了与创建FB15k时相似的Snapshot版本, 有99.54%的三元组都出现在了FB15k中.

作者列举了一个关于长篇小说《A Room With A View》在Freebase中存储的真实样貌, 以便我们更好的来理解Freebase中的各种结构:

能够看到, 在Freebase中存在着大量的逆关系, 几乎每一种关系都能找到它所对应的逆关系.逆关系是导致Data Leakage的主要原因, 模型通过关联逆关系对获得提升.

注意, FB15k中来自Freebase的冗余逆关系是人为创建的, 它被添加了一个反向三元组, 用关系reverse_property显式表示出来.

CVT and Concatenated Edges

在Freebase中, 有一类特殊的节点被称为CVT(Compound Value Type), 其发挥的作用更像中继节点, 以便能更好的处理多元关系. CVT能够作为更抽象的节点被多种二元关系所连接, 而三元组则以合并CVT所连接的两条边后的形式被创建. 例如(Bafta Award For Best Film, award_category/nominees, CVT)和(CVT, award_nomination/ nomated_for, A Room With A View)在奖项和作品之间形成三元组, 对这两种关系$r_1, r_2$ 的合并记为$r_1 . r_2$. CVT常用于更简单的标识某个事件所对应的多种属性.

例如, 关于Obama任职期限的多元关系government_position_held包含了多个子二元关系, offer_holder, office_position, from, to等:

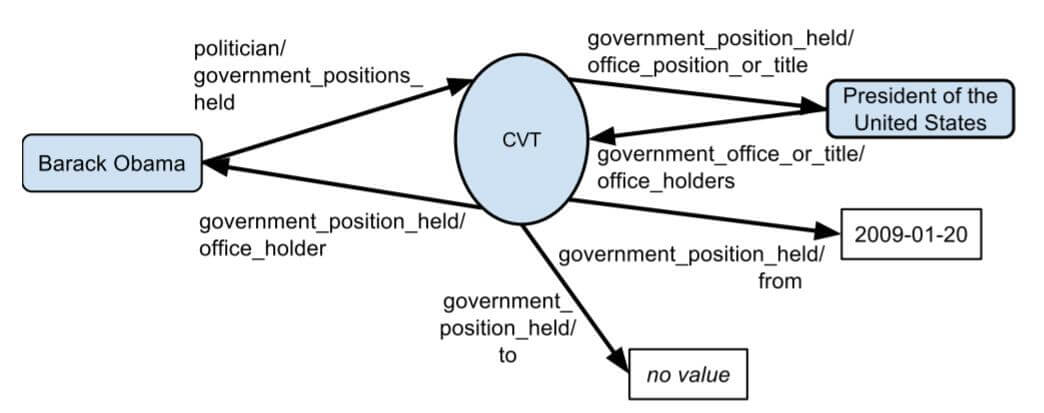
该图片取自From Freebase to Wikidata: The Great Migration.

而在FB15k中, 将大多数的CVT节点合并掉了, 合并的边以三元组的形式出现在FB15k中.

Data Redundancy

Data Redundancy是导致Data Leakage的根本原因. 冗余的数据使得模型倾向于关联各种逆关系对, 从而获得在真实任务中不能获得的额外信息, 导致过拟合.

Data Leakage due to Reverse Triples

前人已经发现, 在FB15k中含有大量的逆关系. 一般的, 对于逆三元组对$(h, r, t), (t, r^{-1}, h)$, 其中的$r$ 被称为逆关系. 实际上在Freebase中, 逆关系已经使用特殊的关系reverse_property来显式关联逆关系对. 例如, (film/directed_by, reverse_property, director/film)意味着film/directed_by和是一对逆关系. 如果是由CVT合并来的两关系$r_1. r_2$, 它们的逆关系理所当然的是$r_2^{-1} . r_1^{-1}$.

FB15k

在FB15k中, 训练集中的48w个三元组中, 有将近34w的三元组形成了17w的逆关系对, 在测试集中约有70.3%的三元组的逆关系能够在训练集中被找到. 这是非常严重的泄露了, 模型非常容易的将自己的训练目标转化为如何才能学习到更多的逆关系对, 从表面上优化在FB15k中的效果.

WN18

在WN18中, 一共有18个关系, 其中有14个关系构成了7对逆关系对, 除此外还有三种对称关系. 在测试集和训练集中包含逆关系对的三元组非常多, 也导致了非常严重的泄露.

Other Redundant Triples

作者指出, 除去表面上已经明确指出的逆关系, 在FB15k中还存在其他类型的语义冗余关系. 作者通过一种简单的衡量标准来判断关系对$(r_1, r_2)$ 中出现的两种关系$r_1, r_2$ 是否是冗余的.

假设$\left| r \right|$ 是关系$r$ 所对应的三元组实例个数, $T_r$ 代表关系$r$ 对应三元组实例中的头实体$h$ 和尾实体$t$ 对的集合, 即$T_r=\{(h, t) \mid r(h, t) \in \mathcal{G} \}$. 如果满足以下条件, 那么称$r_1$ 和$r_2$ 为重复关系:
$$
\frac{\left|T_{r_{1}} \cap T_{r_{2}}\right|}{\left|r_{1}\right|}>\theta_{1} \text { and } \frac{\left|T_{r_{1}} \cap T_{r_{2}}\right|}{\left|r_{2}\right|}>\theta_{2}
$$
其实就是非常简单的去看两种关系所对应的头尾实体对的重合度. 如果两种关系所对应的头尾实体对交集越多, 则证明其对应头尾实体的重合区域就越大, 两种关系也越有可能具有相似的语义, 冗余的可能性也就越大.

更多的, 对于关系$r_1$ 和逆关系$r_2^{-1}$ 也能由之推广而来. $T_r^{-1}$ 代表$T_r$ 的逆实体对, 即$T_r^{-1}=\{(t, h) \mid (h, t) \in T_r \}$. 同样的, 如果满足以下条件, 则称$r_1$ 和$r_2$ 为逆重复关系:
$$
\frac{\left|T_{r_{1}} \cap T_{r_{2}}^{-1}\right|}{\left|r_{1}\right|}>\theta_{1} \text { and } \frac{\left|T_{r_{1}} \cap T_{r_{2}}^{-1}\right|}{\left|r_{2}\right|}>\theta_{2}
$$
作者将$\theta_1, \theta_2$ 在FB15k中设置为0.8.

例如, 关系$r_1$ football_position/players 和关系$r_2$ sports_position/players.football_roster_position/player, 就是一对重复关系, 因为计算得出$\frac{\left|T_{r_{1}} \cap T_{r_{2}}\right|}{\left|r_{1}\right|}=0.87 , \frac{\left|T_{r_{1}} \cap T_{r_{2}}\right|}{\left|r_{2}\right|}=0.97$. 上述两种关系在下图中分别用红色, 绿色标记出:

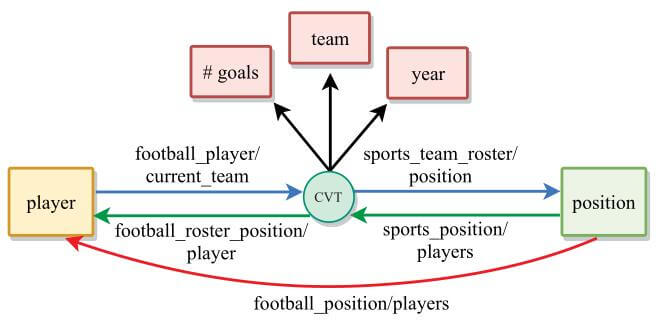
红色的关系记载了每个足球运动员整体的职业生涯所踢的位置, 绿色关系是通过CVT连接而来的, 代表特定时间球员在球队中所处的位置, 属于多元关系. 但实际上, 绝大多数的球员在职业生涯中只踢某一个特定的位置, 所以这两种关系大多数情况下是冗余的. 另一个类似的例子是$r_1$ 和关系$r_3$ football_player/current_team . sports_team_roster/position, 在图中用蓝色标出. $r_1, r_3$ 是逆重复的, 因为计算得出$\frac{\left|T_{r_{1}} \cap T_{r_{2}}^{-1}\right|}{\left|r_{1}\right|}=0.88 , \frac{\left|T_{r_{1}} \cap T_{r_{2}}^{-1}\right|}{\left|r_{2}\right|}=0.97$.

在上述讨论下, 作者将其他的冗余情况分为4种:

训练集中存在逆三元组.
训练集中存在重复三元组或逆重复三元组.
测试集中存在逆三元组.
测试集中存在重复三元组或逆重复三元组.

作者将上述四种情况用四位二进制码来表示, 并统计了FB15k中的测试集冗余情况:

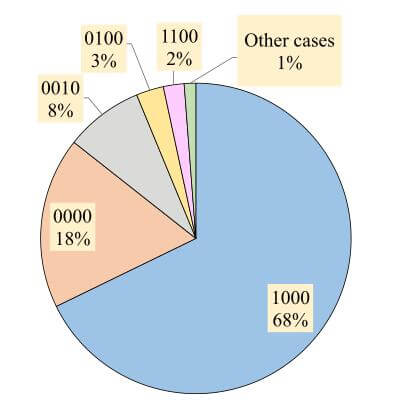
从中能够看出, 68%的三元组集中在1000, 即训练集中存在逆三元组. 没有出现作者所归纳出的四种问题的三元组0000也占了18%, 只在测试集中存在逆三元组的0010占了8%. 其余情况占少部分.

Cartesian Product Relations

笛卡尔积关系在之前的研究中并没有被提出过, 作者第一次发现了这种特殊的关系. 我们首先来回顾一下笛卡尔积. 集合$A=\{a_1, a_2\}, B=\{b_1, b_2, b_3\}$, 假设用$\times$ 来表示笛卡尔积, 那么有:
$$
\begin{aligned}
A\times B &= \{(a_x, b_y)\mid x\ in (1, 2), y \in (1, 2, 3)\}\\
&=\{(a_1, b_1), (a_1, b_2), (a_1, b_3), (a_2, b_1), (a_2, b_2), (a_2, b_3)\}
\end{aligned}
$$
如果将笛卡尔积用于三元组中, 那么对于笛卡尔积关系$r$, 其对应的头实体$h$ 和尾实体$t$ 总是符合笛卡尔积的运算关系, 即$h \in \mathcal{H}, t \in \mathcal{T}$, 关系$r$ 中的头尾关系实体对应该为$\mathcal{H} \times \mathcal{T}$, $\mathcal{H}$ 到$\mathcal{T}$ 中的每个实体都存在关系$r$.

例如, 关系climate, 通常以(a, climate, b) 的形式出现在现实生活中, 其中a为城市, b为月份. 但实际上, Link Prediction在这种三元组上做的预测毫无意义. 例如链接预测在climate上的意义会转化为某城市在几月份是否有气候.

再假设一个场景, Tokyo与CVT相连, 边上的Label为climate, January与CVT相连, 边上的Label为month, 34与CVT相连, 边上Label为average_min_temp_c. 这个关系代表东京一月份的平均低温为34度, 但人们实际上在现实世界中更关心平均气温, 而不是将链接预测用于此预测一月是否有温度. 根本原因是现实世界的多重关系与链接预测任务将其简化为多重二元关系, 而多重二元关系在拆解开后不能恢复成多元关系.

此外, 负采样获得的三元组也有可能是正确的, 而笛卡尔积关系在这个问题上尤为突出.

在笛卡尔积关系大量出现在数据集中时, 会拉高整体模型的评估精度. 这种特殊性使得笛卡尔积与其他关系放在一起比较不太公平, 作者在论文中给出的建议是, 将笛卡尔积关系和非笛卡尔积关系分别比较.

作者仍然尝试使用简单的方法来检测笛卡尔积关系, 对于关系$r$, 其头实体集$S_{r}=\{\mathrm{h} \mid \exists \ r(\mathrm{h}, \mathrm{t}) \in \mathcal{G}\}$, 尾实体集 $O_r = \{\mathrm{t} \mid \exists \ r(\mathrm{h}, \mathrm{t}) \in \mathcal{G}\}$, 若$|r| /\left(\left|S_{r}\right| \times\left|O_{r}\right|\right)$ 高于了某个阈值(之前设置的为0.8), 则认为该关系是笛卡尔积关系.

尽管笛卡尔积关系不像逆关系数量那么多, 但是笛卡尔积关系非常容易被模型学习到, 下图为FB15k - 237中部分笛卡尔积关系的FMRR:

作者尝试证明自己的假设, 观察笛卡尔积关系所带来的影响. 如果笛卡尔积关系能被检测到, 则在链接预测时直接从已知的笛卡尔积头尾实体对的候选集中随机排序, 挑选合适的头尾实体.

随机排序是我在代码中看到的, 并不是很确定正确与否, 作者在论文中并没有明确指出.

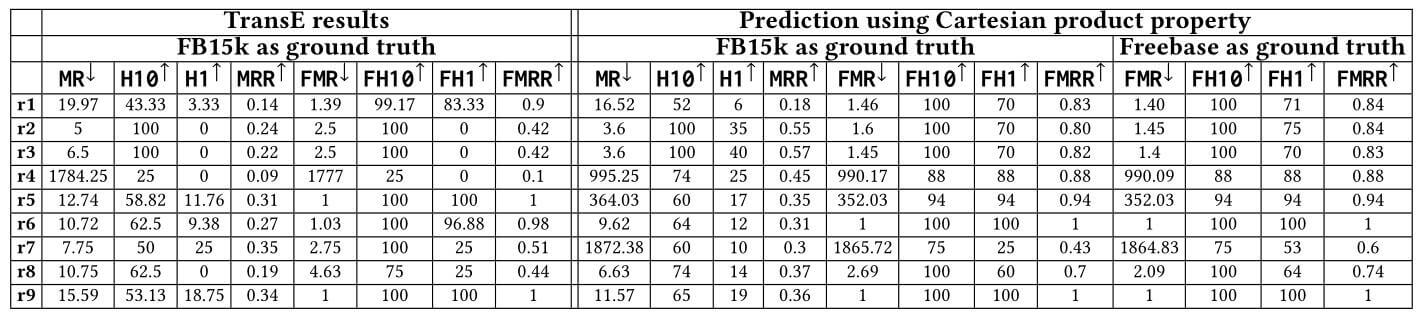
下图为单纯使用TransE在笛卡尔积关系上的表现和利用笛卡尔积特性后的模型表现:

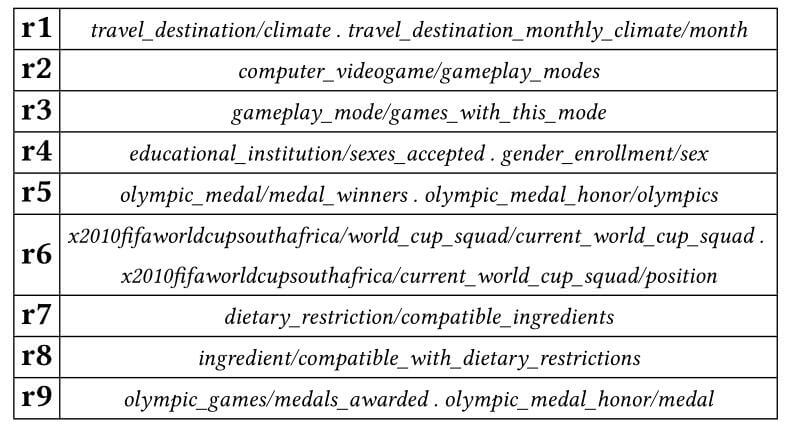
下图为上图中所有关系的具体含义:

能从结果中观察到, 利用笛卡尔积特性的效果比单纯使用TransE要更好. 使用Freebase效果要比它的子集FB15k更强一些.

Experiments

FB15k - 237, WN18RR, YAGO3 - 10 - DR是三种去除逆关系后数据集, 基本上消除了论文中提到的逆关系带来Leakage的问题.

FB15k - 237中, 删除逆关系的过程与作者提出的过程本质上一致, 这就有可能存在误伤, 即删除了一些在语义上不冗余的关系, 没有考虑笛卡尔积关系.
WN18RR中, 保留了对称关系(也产生了逆关系对), 数据集中的11种关系中, 有3种是自反关系.
YAGO3 - 10 - DR是作者自制的数据集, 也做了移除逆关系的处理.

Results

作者将诸多流行的Baseline在多种数据集上用链接预测详细测试. 我在写的时候对原文中陈述的顺序进行了调整, 按照数据集将各种结果整合到一起, 方便阅读.

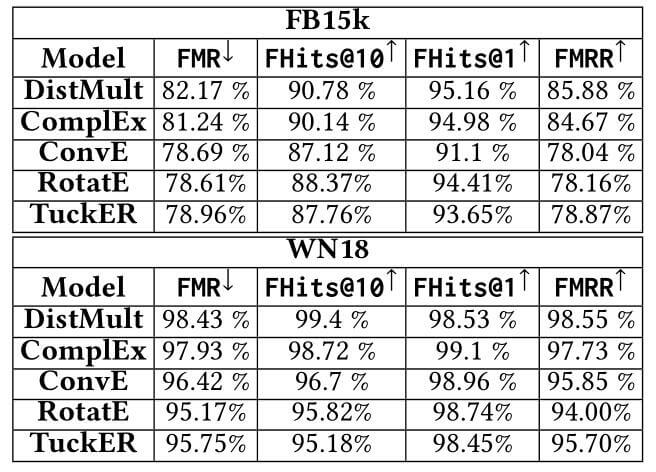
FB15k and FB15k - 237

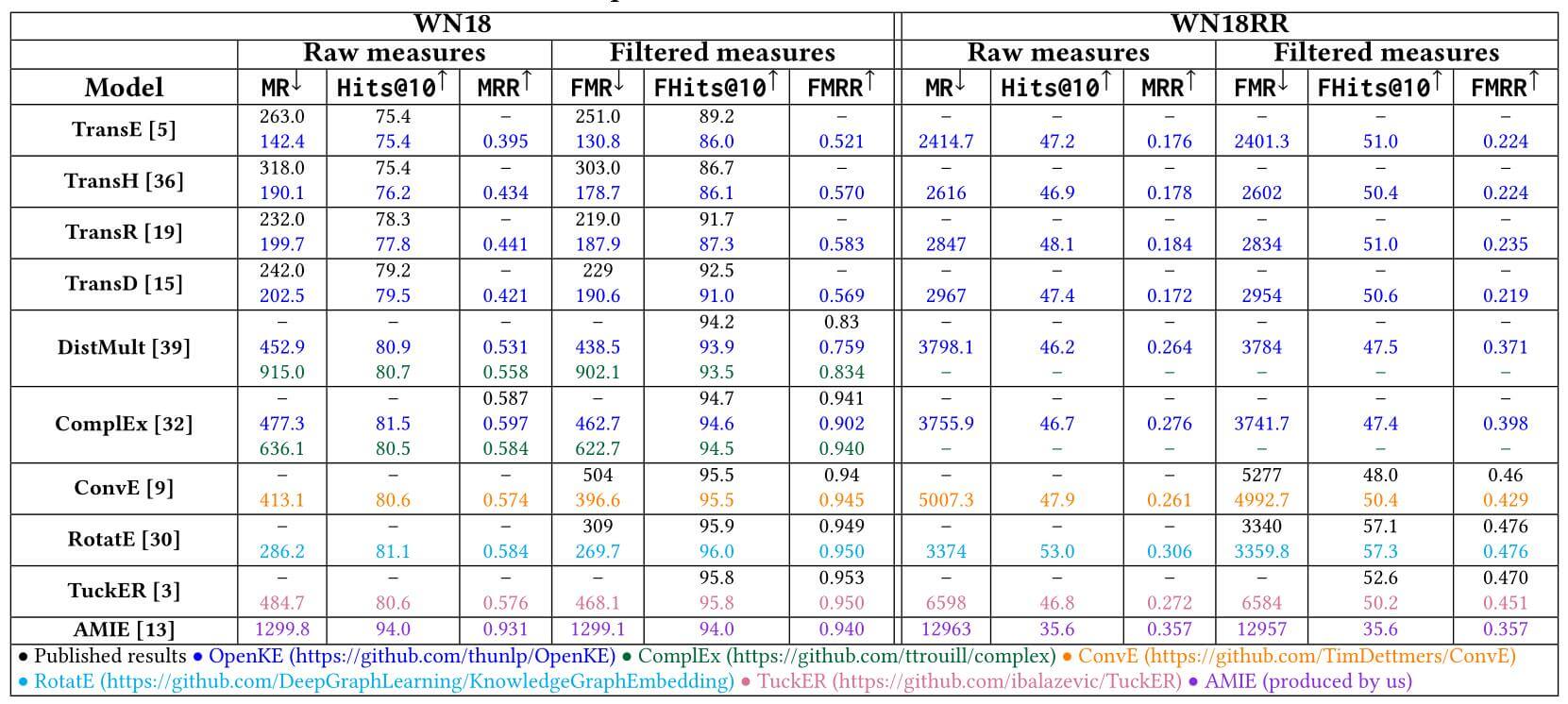
FB15k, FB15k - 237上, 各类模型结果如下:

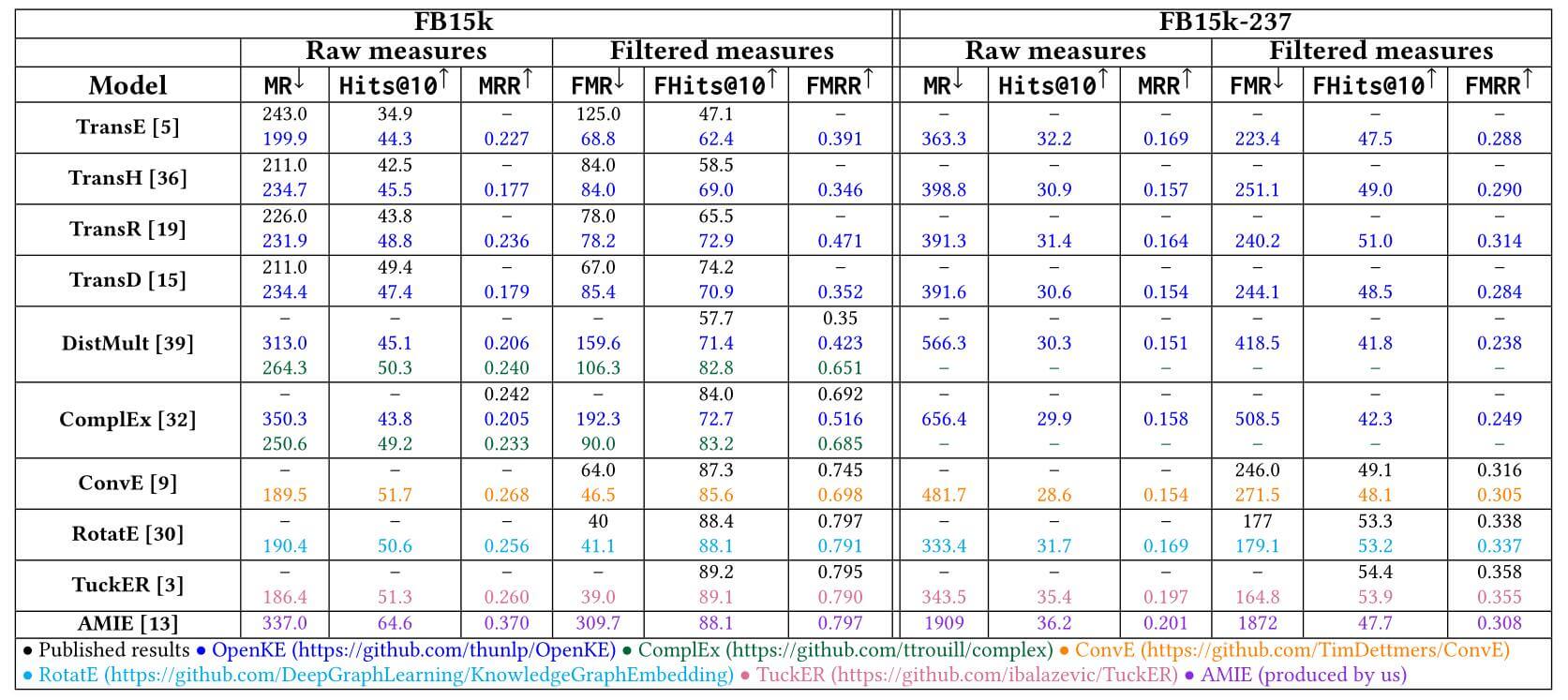
不同颜色的结果代表不同的实验结果来源, 其中AMIE是基于规则的模型.

在将逆关系移除后, 所有的模型结果都发生了明显的退化.

作者进一步精确的分析了模型在数据集中各种关系的性能(以FMRR为指标), 将每个模型在测试集中相较于其他模型性能最好的关系所占百分比. 下图是FB15k - 237的热力图:

为了更好地理解模型优缺点, 作者将上表中的关系分类对待, 根据前面得出的FMRR做出柱状图:

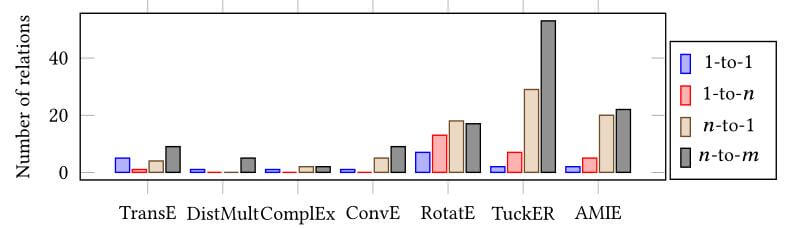
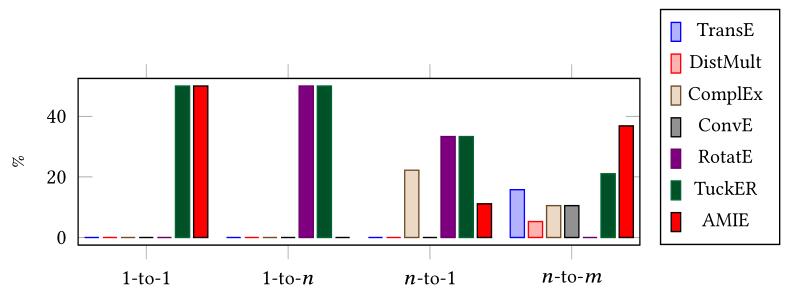
下图为模型在每类别关系表现最优的占比:

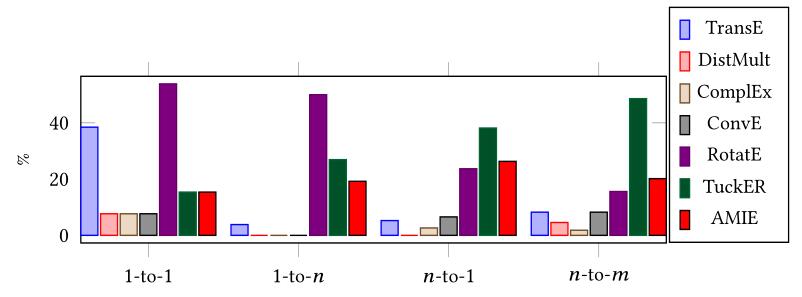
各模型在FB15k - 237区分类别的关系下的FHits@10:

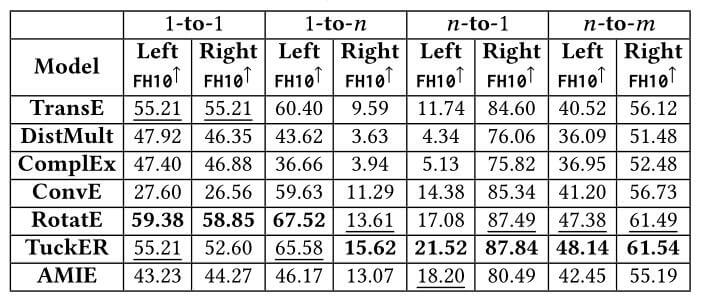
WN18, WN18RR

本小节结构与上小节完全一致. WN18, WN18RR上, 各类模型结果如下:

下图是WN18RR的热力图:

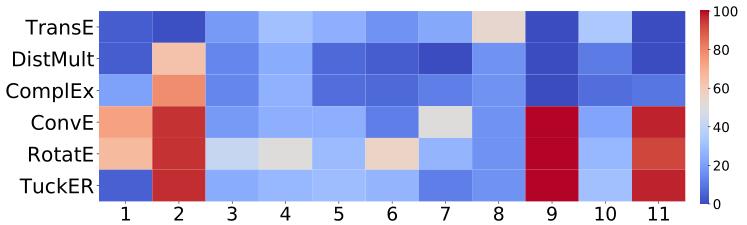
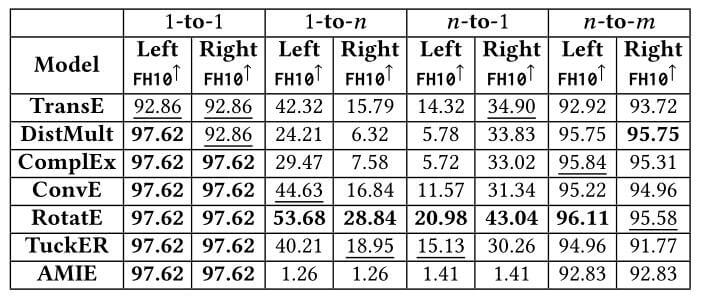
因为WN18RR中含有的关系数量过少, 为了维持实验的稳健性, 所以作者并没有做出与FB15k - 237中类似的柱状图分析. 各模型在WN18RR区分类别的关系下的FHits@10:

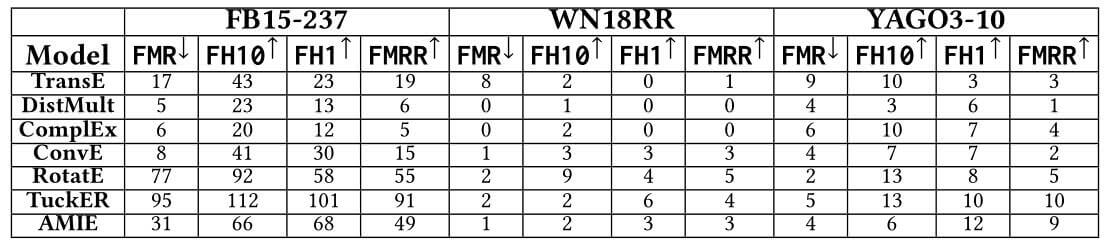
YAGO3 - 10, YAGO3 - 10 - DR

本小节结构与上上小节也完全一致. YAGO3 - 10, YAGO3 - 10 - DR上, 各类模型结果如下:

同样的, 在YAGO 3 - 10上作者也做了同样的可视化:

下图为模型在每类别关系表现最优的占比:

各模型在YAGO3 - 10区分类别的关系下的FHits@10:

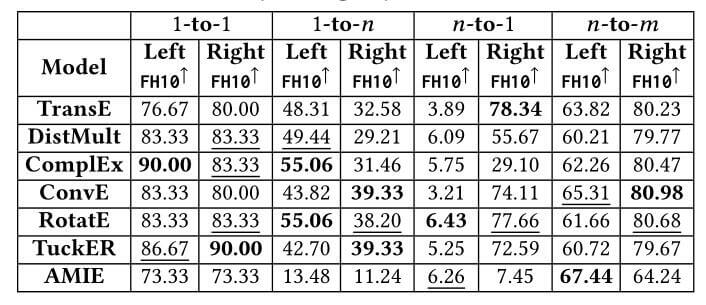
Together

作者假设删除了逆三元组和重复三元组后, 优于TransE的模型并没有体现出很好优势,

下图是在测试集的三元组某指标上优于TransE的模型中, 在训练集中含有逆或冗余三元组所占的百分比:

这证实了在FB15k和WN18上, 大多数比TransE效果好的方法与逆关系或冗余三元组是强相关的, 并且在去掉它们之后, 会有相当大的性能损失.

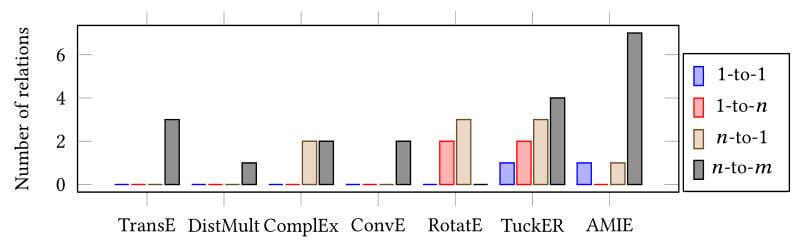
作者进一步的分析了在改进后的数据集上, 不同模型在不同指标中取得最优的关系数量:

从中能观察到, 在移除了包含逆关系的三元组后, 很多模型并不能取得比TransE好太多的效果.

最后, 作者汇总了各模型在各类数据集下的FHits@1:

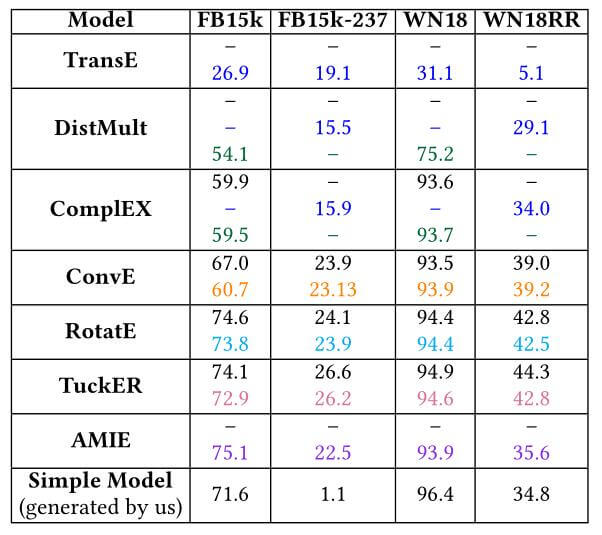
其中, Simple Model是作者提出的一个简单的基于统计信息的模型, 能够自动推断出两个关系能否形成逆关系对, 从而简单的推断出答案. 仅仅使用统计信息在FB15k和WN18上取得了相当好的成绩, 但在FB15k - 237和WN18RR上的成绩非常差, 进一步证明了之前数据集问题的存在性和危害.