TransE: Translating Embeddings for Modeling Multi-relational Data
本文是论文Translating Embeddings for Modeling Multi-relational Data的阅读笔记和个人理解. 这篇论文是一篇比较早的论文了, 2012年Knowledge graph这个概念被谷歌提出, 2013年这篇论文就发表了, 并且大家也对它认可度很高, 几乎之后的所有关于KGE的论文中都会出现以它为Baseline的实验.
Basic Idea
在有向图中, 可以允许有多元关系数据的存在, 例如图中的边可以被表示为$ (head, label, tail) $, 即$(h, \ell, t)$. 这点经常体现在各种知识库中, 比如Google的知识图谱.
在先前的Knowledge Embedding方法中, 要么具有很高复杂度, 要么有高计算成本.
作者阐述, 基于平移的模型主要来源于下列两个Motivation:
- 最主要的Motivation是在很多KBs中, 层次化表示都非常的常见, 那么平移一种很自然的转换表示法. 比如树的自然表示就可以用兄弟关系和父子关系来投射到一个二维坐标系中表示. 所以可以尝试可以把三元组嵌入到低维空间中.
- 类似与Word2vec, 作者观察到Word Embedding能够捕获一些文本中的一对一关系, 例如国家和城市之间的”省会”关系, 在嵌入空间上就是平移.
Translation - Based Model
TransE的思想其实是非常简单的. 对于三元组$(h, \ell, t)$, TransE希望能够在空间中有$h+\ell \approx h$, 即$h+\ell$ 离$t$ 最近, 离其他的尾实体$\ell^{\prime}$非常远. 用$d(h+\ell^{\prime}, t)$ 代表二者间不相似的程度, 其中使用的不相似度度量$d$ 可以是L1范数, 也可以是L2范数等等.
TransE Algorithm
其实明白了TransE的思想, 算法的流程也就不难明白. 算法伪代码如下:

基本分为如下几步:
- 用均匀分布初始化关系和实体矩阵.
- 进入循环, 每次循环开始都对实体$e$ 归一化.
- 从三元组中采样出一个Minibatch来.
- 对每个Batch中的三元组进行替换, 主要是替换头实体或者尾实体生成负样本, 将打乱后的数据(负样本)和原来正确的三元组(正样本)和放到一个集合中.
- 对集合中的样本按照损失函数梯度对Embedding进行更新.
与SVD一样, 采用最大化间隔作为损失函数:
$$
\mathcal{L}=\sum_{(h, \ell, t) \in S} \sum_{\left(h^{\prime}, \ell, t^{\prime}\right) \in S_{(h, \ell, t)}^{\prime}}\left[\gamma+d(\boldsymbol{h}+\boldsymbol{\ell}, \boldsymbol{t})-d\left(\boldsymbol{h}^{\prime}+\boldsymbol{\ell}, \boldsymbol{t}^{\prime}\right)\right]_{+}
$$
其中$\gamma$ 是超参数, 代表间隔. $[x]_+$ 代表取$x$ 的正的部分, 其实就是ReLU.
这个损失函数的意义是, 希望能够最小化正例三元组在空间中的距离, 最大化负例三元组在空间中的距离.
其中$S^{\prime}$ 来自正确三元组替换头实体或尾实体的集合:
$$
S_{(h, \ell, t)}^{\prime}=\left\{\left(h^{\prime}, \ell, t\right) \mid h^{\prime} \in E\right\} \cup\left\{\left(h, \ell, t^{\prime}\right) \mid t^{\prime} \in E\right\}
$$
Dissimilarity Function
正如我们之前所说, 不相似度度量可以使用L1或L2范数, 这里作者直接使用L2范数:
$$
d(\boldsymbol{h}+\boldsymbol{\ell}, \boldsymbol{t})= \lVert\boldsymbol{h} \rVert_{2}^{2}+
\lVert\ell\rVert_{2}^{2}+
\lVert\boldsymbol{t}\rVert_{2}^{2}-2\left(\boldsymbol{h}^{T} \boldsymbol{t}+\boldsymbol{\ell}^{T}(\boldsymbol{t}-\boldsymbol{h})\right)
$$
那么$h+\ell$ 与$t$ 越近, 不相似度就越低(越相似), 反之不相似度就越高(越不相似). 因为每个Batch都对实体做归一化, 所以还有$\lVert\boldsymbol{h}\rVert_{2}^{2}=\lVert\boldsymbol{t}\rVert_{2}^{2}=1$.
Some Explain
在优化时使用SGD, 并且在训练过程中, 作者提出的算法只对每个Batch更新时的实体进行了归一化, 关系没有做要求, 在此作者没有说明原因.
Experiments
DataSets
因为是比较早的KGE方法, 作者只在WN, FB15k, FB1M上进行了对比.
Evaluation protocol
评估阶段的协议非常重要, 直到现在, 很多模型也都遵循着TransE的协议.
对每个测试三元组移除头实体, 并用其他实体轮流替换, 按照Loss升序排列, 最后再计算正确的三元组Loss. 然后对每个尾实体做相同的操作.
可能在替换后, 三元组是仍然正确的. 如果不做任何过滤的操作, 这个被替换后仍然正确的三元组将被记为错误, 这样就可能会低估模型能力. 所以应该将已经在训练集, 验证集, 测试集中出现的三元组从替换后的三元组中剔除, 从而保证在替换头实体或尾实体后三元组一定是错误的. 这种方法被称为Filtered setting, 没有经过过滤的称为raw, 该方法在其他很多论文中都出现过.
Link Prediction
在实体链接上的结果如下:
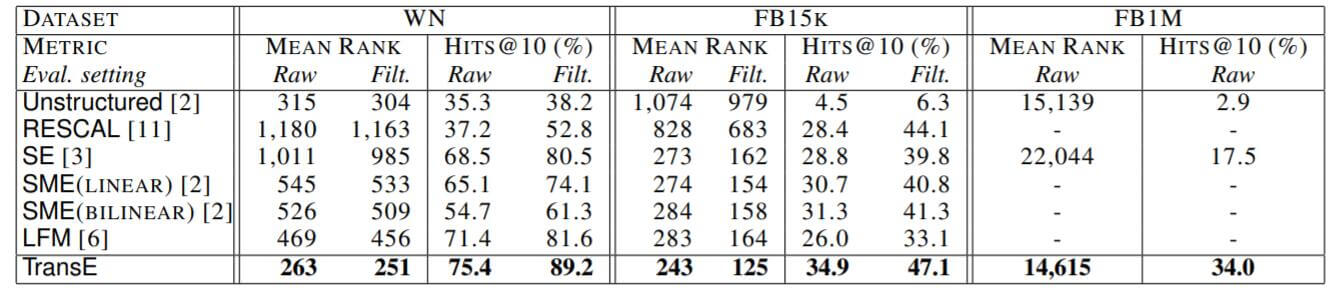
结果分为了两类, 有些指标在Raw和Filtered上表现差距非常大, 说明Filtered Setting还是非常有必要的.
在和Baseline模型相比较时都显示出TransE的强大.
之后作者又在FB15k上做了区分类别的实体链接实验:

能够很清楚的看出, TransE在一对一的建模能力上要好于其他Baseline模型, 并且在预测头实体时一对多, 预测尾实体时多对一时本身的效果比较好, 但不及于其他模型.
Case Study
作者将预测尾实体时的一些案例放了出来, 其中粗体表示测试集中的正确元组, 斜体表示训练集中预测正确的元组.
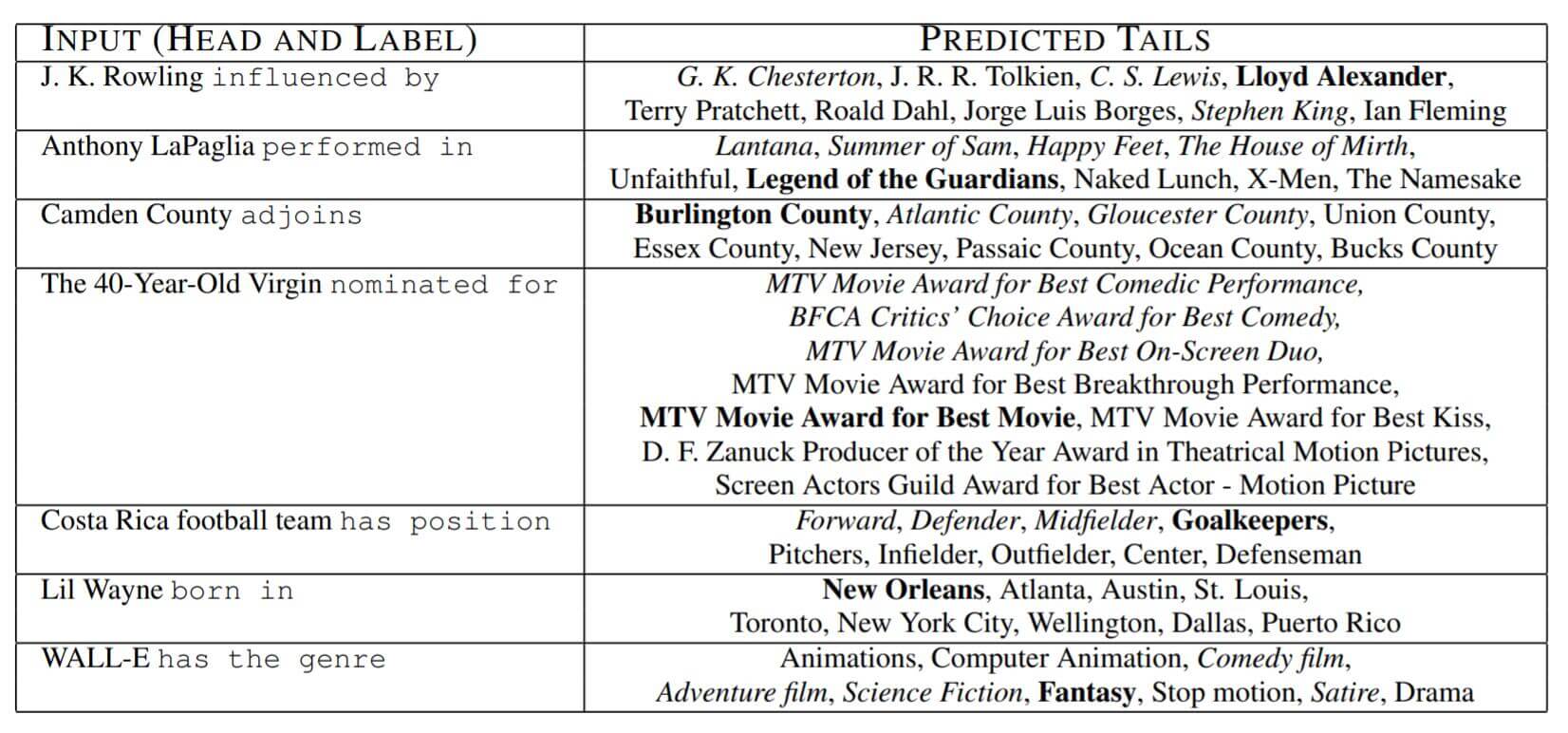
虽然在最高位的不是最佳答案, 但也说明了TransE能够表示一些常识.
Generalization Ability
在FB15k上, 作者随机选择了40种关系作为FB15k - 40rel, 并将其于三元组全部作为FB15k - rest. 作者只让所有Embedding模型学习这四十个关系所对应的数据, 即只学习FB15k - 40rel, 并对FB15k - rest进行连接预测, 尝试观察TransE的泛化能力:
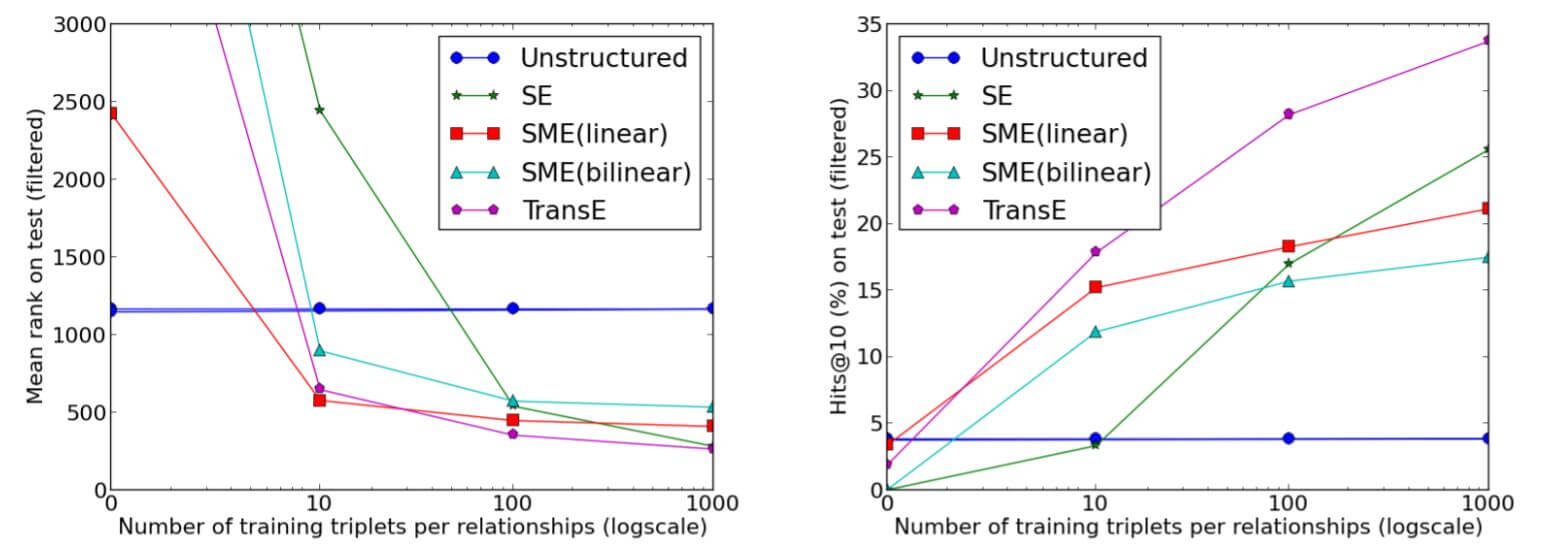
左图是模型在MR上的表现, 右图是Hit@10的表现.
结果表明, TransE是学习速度最快的方法, 即使只有少量三元组, TransE表现仍然不错. 随着知识的数量增大, TransE仍然有进步空间.
Summary
Trans它为KGE世界打开了新的大门, 之后衍生了例如TransR, TransH等不少基于平移的模型. 并且参数量和计算量都不算特别多. 但TransE也有非常多的缺点, 这些问题包括但不限于:
- 一对多建模存在竞争, 即比如$(Writer, Compose, Novel)$这个三元组, 一名作者可以写多部小说, 作品之间是不同的实体. 在TransE中, $Writer + Compose$只能尽可能指向某一部作品, 如果有多部作品就会导致竞争. 多对多同理, 肯定更不擅长了.
- 不能完成对称关系的建模, 例如”朋友”这种关系. 在TransE中, 假设小明和小李是朋友, 用$(Ming, Friend, Li)$ 来表示, 小李被表示为$Ming + Friend$. 但是小明却不能被表示为$Li + Friend$.
- 不能完成自反关系的建模, 例如$(h, r, h)$ 的关系在TransE中完全没有办法表示.
- 没有考虑语义关系.

