本文前置知识:
- GNN
Relational Reflection Entity Alignment
本文是论文Relational Reflection Entity Alignment的阅读笔记和个人理解. 这是我第一次接触关于实体对齐领域的文章.
Basic Idea
整篇文章的出发点都源于作者观察到的两个反直觉的现象:
- 在实体对齐问题中, GNN中使用标准线性变换表现得不好.
- 那些在链接预测上表现很好的Knowledge Embedding Model在实体对齐上表现不好.
针对上述两个现象, 作者说明GNN中约束变换矩阵的重要性, 并提出了统一的实体对齐框架, 将现有的两种主流方法相统一.
Background
因为是第一次接触实体对齐领域的文章, 所以我在这里将实体对齐相关的背景补充上.
实体对齐的目标是检测多源Knowledge Graph中的实体对是否等价, 这对多源知识图谱的合并是至关重要的. 通俗一点说, 在两个KG中, 对于同一种实体可能有两种不同的表述, 通过实体对齐能够将两种表述相统一. 在下一节, 我会补充上实体对齐问题的数学描述.
Translation - Based Methods
基于平移的方法灵感来自于Word Embedding中的跨语言表示方法, 例如TransE等, 在实体对齐领域使用时, 有一个非常重要的假设: 在不同的Knowledge Graph中各实体的相对位置是相似的.
一般分为两个模块, Translation Module和Alignment Module.
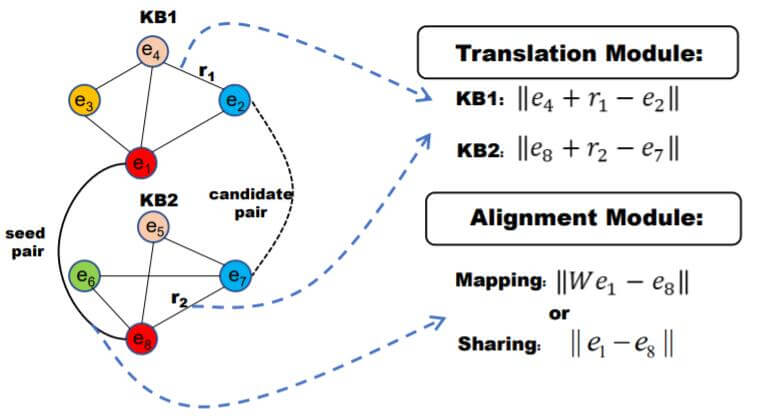
Translation Module
平移模块负责学习到两个KG中相似的实体位置分布, 例如最简单的TransE使用$h+r\approx t$ 来学习位置分布.
Alignment Module
对齐模块负责将两个KG中的实体做对齐. 在Translation Based Model中, 一般有两种方式:
Mapping: 使用变换矩阵将两个KG中的实体统一到一个空间中最小化它们的距离. 例如$W e_{1} \approx e_{2}$ 或 $W_{1} e_{1} \approx W_{2} e_{2}$.
Sharing: 更为激进, 直接共享两个KG中实体的Embedding. 例如在MTransE中通过最小化$||\boldsymbol{e}_{1}-\boldsymbol{e}_{2}||$ 达到共享的效果.
GNNs - Based Methods
受孪生网络启发, 大多方法使用两个多层的GNN编码, 再加上额外的损失函数. 与基于平移的方法不同, 基于平移的方法使用独立的三元组, 而缺少了实体和关系的全局信息, GNN摆脱了三元组的束缚, 依靠聚合从邻居节点获取实体的Embedding.
在获取完不同KG中的实体Embedding后, 采用Contrastive Loss或Triplet Loss来对齐实体:
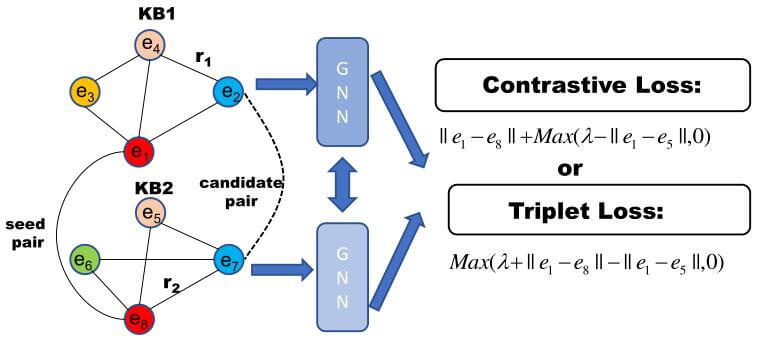
许多基于GNN的方法中经常约束变换矩阵为对角阵或单位阵, 但从未交代原因.
Preliminary
本节描述实体对齐任务的数学描述, 并介绍后续实验中使用的数据集, 为接下来的内容做铺垫.
Problem Formulation
一般的KG都定义为$G=(E,R,T)$, 其中$E,R,T$ 分别代表实体, 关系, 和三元组的集合.
实体对齐的目标是找到两个不同源的KG中的等价的实体对, 例如$G_1, G_2$ 分别为两个不同源的KG, 对齐的实体对表示为:
$$
P=\left\{\left(e_{i_{1}}, e_{i_{2}}\right) \mid e_{i_{1}} \in E_{1}, e_{i_{2}} \in E_{2}\right\}_{i=1}^{p}
$$
模型应该能够利用已知的对齐好的实体来预测新的实体对.
DataSets
在后续的实验中, 作者主要使用了两种数据集:
- DBP15K: 跨语言数据集, 其中含有中文(ZH), 英文(EN), 日语(JA), 法语(FR)的数据. 包括三种跨语言的对齐实体对, 分别是ZH - EN, JA - EN, FR - EN.
- DWY100K: 跨KG数据集, 它是从DBpedia, Wikidata, YAGO3中抽取出来的. 包含两个不同源KG的对齐实体对集, 分别是DBpedia - Wikidata, DBpedia - YAGO3.
具体信息如下:
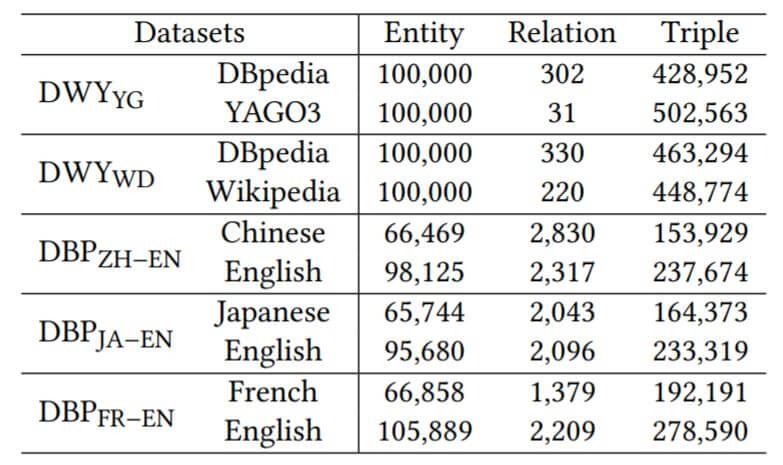
Unified Entity Alignment Framework
在本节中, 作者抽取了基于平移的模型和基于GNN的共性, 将二者统一到一个框架下.
Shape - Builder & Alignment
Shape - Builder
Shape - Builder的主要任务是将随机初始化的实体分布调整到合适形状的分布. 例如上图中, 其实任何Knowledge Embedding Model都可以做为Shape - Builder. 但是仍然要注意前提条件, 等价实体在不同空间中具有相似的分布.
Alignment
当空间相似性保持时, 就能够使用Mapping之类的手段对齐实体:
$$
\min _{W} \sum_{\left(e_{i}, e_{j}\right) \in P}||\boldsymbol{W} \boldsymbol{h}_{e_{i}}-\boldsymbol{h}_{e_{j}}||
$$
其中$(e_i, e_j)$ 是已知对齐的实体对. $\boldsymbol{h}_{e_i}$ 代表实体$e_i$ 的Embedding.
但是, 当变换矩阵$\boldsymbol{W}$ 不加以任何约束时, 空间相似性是极其容易被破坏的. 除非$\boldsymbol{W}$ 能够满足正交性来保证空间中的实体只是经过旋转操作, 而不改变它们之间的相对位置.
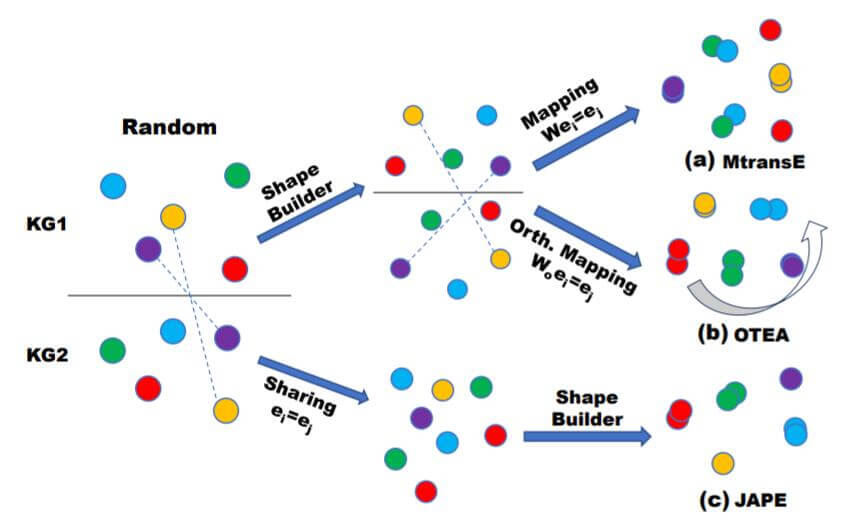
在上图中有:
- (a): MTransE没有约束变换矩阵$\boldsymbol{W}$, 所以在对齐后产生了一些混乱.
- (b): OTEA对矩阵加以正交约束, 比较好的对齐了实体.
- (c): JAPE直接对两个Knowledge Graph使用相同的实体嵌入, 最后再做Shape - Building操作, 也取得了比较好的效果.
GNNs - Based Methods Are Also Subject to Unified Framework
GNN Based Methods
GNN的循环迭代由聚合和更新两部分组成:
聚合:
$$
h^l_{N_{e_{i}}^{e}} \leftarrow \text { Aggregate }\left(\left\{\boldsymbol{h}_{e_{k}}^{l}, \forall e_{k} \in\left\{e_{i}\right\} \cup \mathcal{N}_{e_{i}}^{e}\right\}\right)
$$
聚合时包括了节点自身到自身的特征, 即视为节点有一条自己到自己的闭环.
聚合方式$\text{Aggregate}$有多种, 在GCN中是求平均, 在GAT中是加权求和, 不详细展开说了.
更新:
$$
h_{e_{i}}^{l+1} \leftarrow \sigma\left(\boldsymbol{W}^{l} \cdot h_{\mathcal{N}_{e_{i}}^{e}}^{l}\right)
$$
对邻居节点信息使用第$l$ 层的变换矩阵$\boldsymbol{W}^l$, 能获得更好的节点表示.
损失函数:
基于GNN实体对齐方法的损失函数能使等价实体更近, 让不相关的实体更远:
$$
L=\sum_{\left(e_{i}, e_{j}\right) \in P} \mathop{\underline{\lVert\boldsymbol{h}_{e_{i}}-\boldsymbol{h}_{e_{j}}\rVert}}
\limits_\text {alignment}
+
\sum_{\left(e_{i}^{\prime}, e_{j}^{\prime}\right) \in P^{\prime}} \max \left(
\mathop{
\underline{\lVert\boldsymbol{h}_{e_{i}^{\prime}} - \boldsymbol{h}_{e_{j}^{\prime}}\rVert+\lambda}}\limits_{\text {apart}}, 0
\right)
$$
其中$\lambda$ 为间距, $(e_i^\prime, e_j^\prime)$ 代表从$(e_i, e_j)$ 中随机替换一个实体的负样本实体对.
有了Translation Based Models的基础, 这里能很容易的发现, 损失中的第一项$\lVert\boldsymbol{h}_{e_{i}}-\boldsymbol{h}_{e_{j}}\rVert$ 正巧和作者前面提到的Sharing Aligment一致, 而第二项$\lVert\boldsymbol{h}_{e_{i}^{\prime}} - \boldsymbol{h}_{e_{j}^{\prime}}\rVert+\lambda$恰巧和前面提到的Shape - Builder作用相同. 因此基于GNN的方法也可以视为作者提出的统一框架中的一种. 假设基于GNN的方法也属于作者提出的统一框架的一种, 那么经过GNN进行实体对齐后, 一定能保留量KG中实体对的相似性. 下面作者就要通过实验来证明该猜想.
Visual Experiment
作者使用最简单的GCN - Align, 保留Triplet Loss, 将GCN从监督模型转化为自监督模型:
$$
L_{\text {apart}}=\sum_{\left(e_{i}^{\prime}, e_{j}^{\prime}\right) \in P^{\prime}} \max \left(\lambda-\lVert\boldsymbol{h}_{e_{i}^{\prime}}-\boldsymbol{h}_{e_{j}^{\prime}}\rVert_{1}, 0\right)
$$
用T - SNE对两个法语和英语的多个实体对齐后的结果进行降维可视化:

经过GCN对齐后的实体分布确实有很大的相似性.
Quantitative Experiment
光有可视化分析还不够, 作者希望进行量化实验. 作者提出了Shape Similarity来衡量两个Knowledge Graph中任意两实体构成实体对后的相对距离的差距:
$$
SS=\frac{\sum_{\left(e_i, \tilde{e_i}\right) \in P} \sum_{\left(e_j, \tilde{e_j}\right) \in P}dist(e_i, e_j) - dist(\tilde{e_i}, \tilde{e_j})}{\sum_{\left(e_i^{\prime}, \tilde{e_i}^{\prime}\right) \in P^{\prime}} \sum_{\left(e_j^{\prime}, \tilde{e_j}^{\prime}\right) \in P^{\prime}}dist(e_i^{\prime}, e_j^{\prime}) - dist(\tilde{e_i}^{\prime}, \tilde{e_j}^{\prime})}
$$
其中, $e_i, e_j \in G_1, \tilde{e_i}, \tilde{e_j} \in G_2$. $e_i, e_j$ 为$G_1$ 中的任意两实体构成的实体对, $\tilde{e_i}, \tilde{e_j}$ 为$G_2$ 中相应的实体构成的实体对. $({e_i}^{\prime}, \tilde{e_i}^{\prime}, {e_j}^{\prime}, \tilde{e_j}^{\prime})$ 代表$({e_i} , \tilde{e_i} , {e_j} , \tilde{e_j} )$ 中随机替换一个负例实体后的四元组. 故$P$ 代表有效的对齐实体对, $P^{\prime}$ 代表无效的负采样的负例实体对.
因此, 分子为对齐实体之间的相对距离差, 分母为随机实体对之间的距离差. 如果两个KG中的实体分布相似, 分子应该尽可能的小, 分母尽可能的大.
作者测试了随机分布, TransE, GCN(未训练), GCN对齐后的结果:
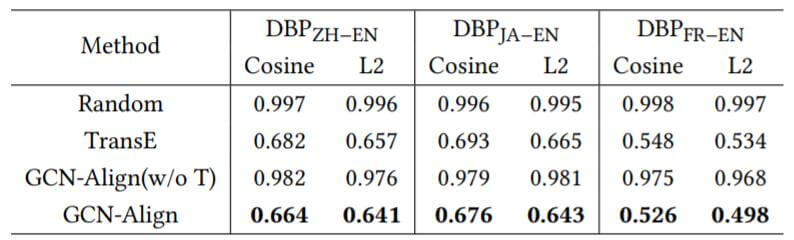
这符合作者的预先设想, 随机和未训练的GCN对齐后的余弦距离都非常大, 接近于1. TransE效果比GCN - Align要稍差一些.
Why Linear Transformation Not Work
基于前文提到的假设, 作者开始对标准线性变换在GNN中不Work的原因分析.
对于$\boldsymbol{W}$ 加以正交约束或不加约束实际上对应着Translation Based Model中的两种情况:
- 当$\boldsymbol{W}$ 为正交矩阵或者单位矩阵$\boldsymbol{I}$ 时, 本质上就等价于Translation Based Model中的Sharing Alignment.
- 当$\boldsymbol{W}$ 不加以约束时, 本质上等价于Translation Based Model中的Mapping Alignment. 这可能会破坏掉数据集中的空间分布相似性.
Experiment on GCN - Align
作者使用最简单的GCN在实体对齐任务上, 对加以各类约束和不加约束的设置做了实验, 采用Loss来保证变换矩阵$\boldsymbol{W}$ 的正交性:
$$
L_{o}=\lVert\boldsymbol{W}^{T} \boldsymbol{W}-\boldsymbol{I}\rVert_{2}^{2}
$$
实验结果如下:
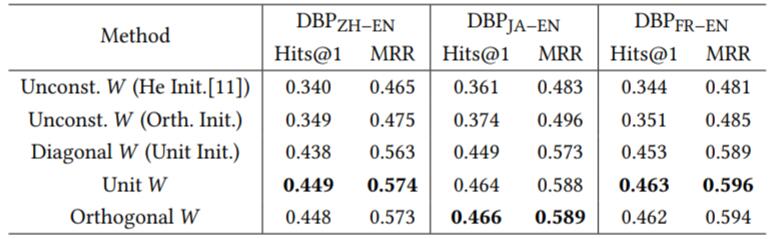
在加以正交约束后, 将近涨了10个点. 这足以说明作者的假设成立. 更一般的, 作者发现, 使用更加简单的单位阵比正交矩阵的效果要稍好一些.
Experiment on Complex GNNs
作者认为对更加复杂的GNN方法做探究也是有必要的, 所以作者也测试了其他GNN方法在使用单位阵或正交阵作为$\boldsymbol{W}$ 的性能:
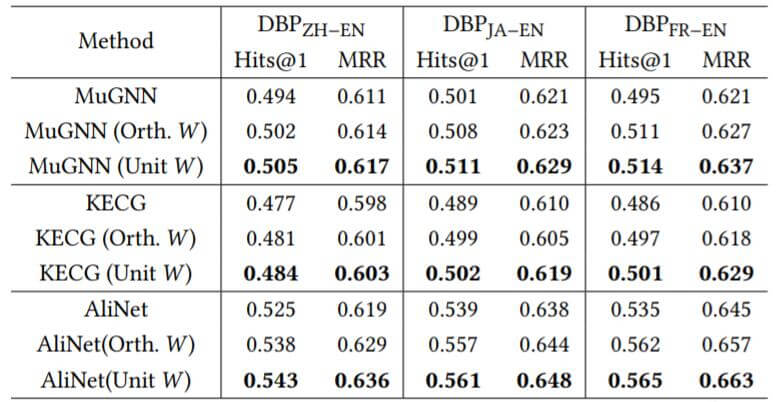
对于更加复杂的方法, 加以约束仍然能取得更好的效果, 使用单位阵作为$\boldsymbol{W}$ 的结果总是比单纯正交约束要好一些. 作者猜测复杂的方法中所包含的变换矩阵更多, 使得正交约束的优化有些困难.
Why Advanced KG Embedding Not Work
作者将在链接预测上表现比较好的模型在实体对齐中做了测试:
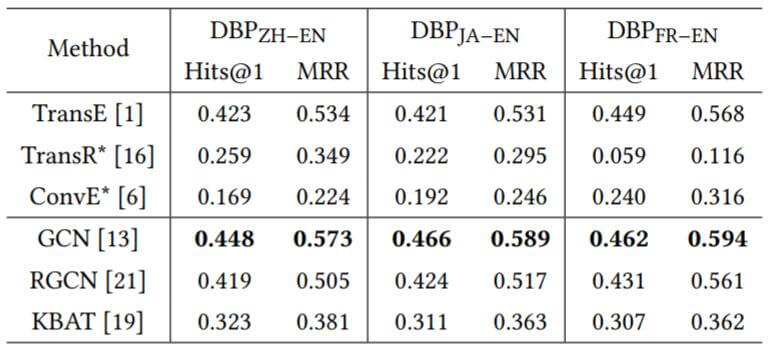
很多在链接预测中表现很好的KGE模型, 在实体对齐中效果很差, 至少比简单的TransE效果差17%, 而基于GNN的方法比GCN至少差3%. 作者将它们汇总在下表中:

其中$\mid\mid$ 代表Concat, $\ast, \omega$ 分别代表卷积操作和卷积核. $d_i$ 代表实体$e_i$ 的度(GCN中需要用到度矩阵来衡量节点的重要性).
KGE方法本质上的思想都是将实体嵌入转换为特定的关系嵌入.
对于这句话, 我认为可以这样理解, 在列出的模型中, 在训练时必然离不开关系$r$, 其实学习实体嵌入也是为了学习到关系$r$ 的表示, 因为关系的嵌入表示不可能在不依靠实体的情况下学习到.
在基于平移的模型中, 头实体$h$ 更像是锚点, 经过关系$r$ 的作用后能够确定尾实体$t$, 通过调整$r$ 能决定$t$ 的落点. 基于GNN的模型以节点为单位学习, 也将关系隐式表现在节点与邻居节点的聚合之间.
作者也指出, 尤其是RGCN是GCN和TransR的结合, KBAT是ConvE和GAT的结合.
作者发现, 在最初的设计中, 所有的模型都没有对它们的变换矩阵加以约束, 从而违背了变换矩阵需要满足的正交结论.
作者提到, 现在的方法很难在实际中做到正交. 例如TransR和RGCN不可能同时约束KG中非常多的关系. ConvE和KBAT在转换后的嵌入维度必须与输入维度保持一致, 否则会发生尺寸不匹配, 因此ConvE和KBAT的变换矩阵不能是方阵, 更不可能是正交阵.
Key Criteria for Transformation Operation
根据作者分析的问题, 作者提出了两种理想状态下的实体对齐变换标准, 对实体对齐操作加以约束.
Relation Differentiation
对于不同的关系类型, 作者希望将统一实体在不同关系下的表示变得不同:
$$
\varphi\left(\boldsymbol{h}_{e}, \boldsymbol{h}_{r_{1}}\right) \neq \varphi\left(\boldsymbol{h}_{e}, \boldsymbol{h}_{r_{2}}\right), \forall e \in E, \forall r_{1}, r_{2} \in R
$$
这一约束避免了模型学习到同实体在不同关系下的相同表示, 从而不能区分开关系之间的不同.
Dimensional Isometry
同一KG下的两个实体转换进同一关系空间时, 它们之间的范数和相对位置应该保持不变:
$$
\begin{array}{c}
\lVert\boldsymbol{h}_{e}\rVert=\lVert\varphi\left(\boldsymbol{h}_{e}, \boldsymbol{h}_{r}\right)\rVert, \forall e \in E, \forall r \in R \\
\boldsymbol{h}_{e_{1}}^{T} \boldsymbol{h}_{e_{2}}=\varphi\left(\boldsymbol{h}_{e_{1}}, \boldsymbol{h}_{r}\right)^{T} \varphi\left(\boldsymbol{h}_{e_{2}}, \boldsymbol{h}_{r}\right), \forall e_{1}, e_{2} \in E, \forall r \in R
\end{array}
$$
第一个约束保证了在经过关系变换后, 实体的Embedding范数与没变化时相同.
第二个约束保证了在经过关系变换后, 两实体的相对位置不发生变化(点积不变).
The Proposed Method
在本节中, 作者依托上节中提出的两个操作, 提出了一种基于GNN的新实体对齐方法RREA(Relational Reflection Entity Alignment).
Relational Reflection Transformation
令关系嵌入$\boldsymbol{h}_r$ 为法向量, 其垂直的超平面为$\boldsymbol{P}_r$, 使用与关系相关的反射矩阵$\boldsymbol{M}_r$ 来描述实体经过的变换:
$$
\boldsymbol{M}_{r}=\boldsymbol{I}-2 \boldsymbol{h}_{r} \boldsymbol{h}_{r}^{T}
$$
其中$\boldsymbol{h}_r$ 应该是归一化的. 并且, 非常容易能够证明反射矩阵$\boldsymbol{M}_r$ 的正交性:
$$
\begin{aligned}
\boldsymbol{M}_{r}^{T} \boldsymbol{M}_{r} &=\left(\boldsymbol{I}-2 \boldsymbol{h}_{r} \boldsymbol{h}_{r}^{T}\right)^{T}\left(\boldsymbol{I}-2 \boldsymbol{h}_{r} \boldsymbol{h}_{r}^{T}\right) \\
&=\boldsymbol{I}-4 \boldsymbol{h}_{r} \boldsymbol{h}_{r}^{T}+4 \boldsymbol{h}_{r} \boldsymbol{h}_{r}^{T} \boldsymbol{h}_{r} \boldsymbol{h}_{r}^{T}=\boldsymbol{I}
\end{aligned}
$$
因此, 只要不满足$\{\boldsymbol{h}_{r_i}\neq\boldsymbol{h}_{r_j} \forall{r_i, r_j} \in R \}$, 关系反射变换就能够满足在上一节中提出的两个理想标准.
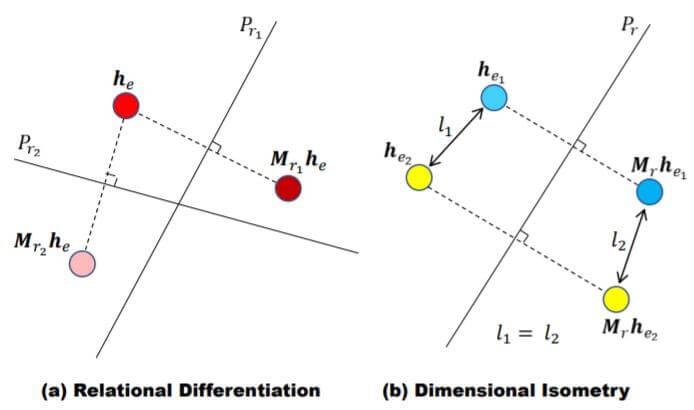
Relational Refection Entity Alignment
下面作者正式介绍RREA. 模型需要输入实体嵌入矩阵$\boldsymbol{H}^{e} \in \mathbb{R}^{|E| \times d}$ 和关系嵌入矩阵$\boldsymbol{H}^{r} \in \mathbb{R}^{|R| \times d}$.
Relational Reflection Aggregate Layer
节点$e_i$ 第$l$ 层的输出特征如下:
$$
\boldsymbol{h}_{e_{i}}^{l+1}=\operatorname{ReLU}\left(\sum_{e_{j} \in \mathcal{N}_{e_{i}}^{e}} \sum_{r_{k} \in R_{i j}} \alpha_{i j k}^{l} \boldsymbol{M}_{r_{k}} \boldsymbol{h}_{e_{j}}^{l}\right)
$$
其中$\mathcal{N}_{e_i}^e$ 为节点$e_i$ 的邻居集, $R_{ij}$ 为节点$e_i$ 到节点$e_j$ 之间的关系集. $\boldsymbol{M}_{r_{k}} \in \mathbb{R}^{d \times d}$ 为关系$r_k$ 的关系反射矩阵, 能够通过节点$e_i$ 和节点$e_j$ 之间的关系$r_k$ 直接使用关系反射变换得到. $\alpha^l_{ijk}$ 是节点$e_i$ 对其经过关系变换后的邻居节点$e_j$ 的注意力权重.
因为$\boldsymbol{M}_{r_{k}}$ 是正交阵, 所以它不像RGCN中的$\boldsymbol{W}_r$ 中含有$d^2$ 个自由度, 而是只含有$d$ 个自由度.
类似于GAT, 注意力权重$\alpha_{ijk}^l$ 由$\beta_{ijk}^l$ 得来:
$$
\alpha_{i j k}^{l}=\frac{\exp \left(\beta_{i j k}^{l}\right)}{\left.\sum_{e_{j} \in N_{e_{i}}^{e}} \sum_{r_{k} \in R_{i j}} \exp \left(\beta_{i j k}^{l}\right)\right)}
$$
$$
\beta_{i j k}^{l}=\boldsymbol{v}^{T}\left[\boldsymbol{h}_{e_{i}}^{l}||\boldsymbol{M}_{r_{k}} \boldsymbol{h}_{e_{j}}^{l}|| \boldsymbol{h}_{r_{k}}\right]
$$
其中$\boldsymbol{v} \in \mathbb{R}^{2d}$ 是可以学习的参数.
$\mathcal{v}$ 的尺寸存疑.
将所有层的输出Concat起来, 能得到实体$e_i$ 的最终特征输出$\boldsymbol{h}_{e_{i}}^{o u t}$:
$$
\boldsymbol{h}_{e_{i}}^{o u t}=\left[\boldsymbol{h}_{e_{i}}^{0}||\ldots||\boldsymbol{h}_{e_{i}}^{l}\right]
$$
这样能够保存全局信息, 而不是只以最后一层的输出作为特征.
Dual - Aspect Embedding
基于一些最近的研究, GNN只能包含拓扑结构信息, 缺少实体附近的关系信息, 因此作者直接将节点附近的关系信息一起Concat起来, 作为实体和关系的共同嵌入$\boldsymbol{h}_{e_{i}}^{M u l}$:
$$
\boldsymbol{h}_{e_{i}}^{M u l}=\left[\boldsymbol{h}_{e_{i}}^{o u t} || \frac{1}{\left|\mathcal{N}_{e_{i}}^{r}\right|} \sum_{r_{j} \in N_{e_{i}}^{r}} \boldsymbol{h}_{r_{j}}\right]
$$
其中$\mathcal{N}_{e_i}^r$ 是节点$e_i$ 的关系集. 这样就包含了GNN对节点本身抽取的节点特征和节点附近的关系特征.
Alignment Loss Function for Training
为了保证等价的实体在统一的空间中接近, 使用三元组损失:
$$
L=\sum_{\left(e_{i}, e_{j}\right) \in P} \max \left(\operatorname{dist}\left(e_{i}, e_{j}\right)-\operatorname{dist}\left(e_{i}^{\prime}, e_{j}^{\prime}\right)+\lambda, 0\right)
$$
其中, $(e_i, e_j) \in P$ 是等价实体对, $e_i^\prime, e_j^\prime$ 是通过最近邻居采样得来的负样本实体对.
注意, 这里的$e_i, e_j$ 和之前描述$SS$ 时的意义是不一样的.
然后采用与GCN - Align相同的距离度量:
$$
\operatorname{dist}\left(e_{i}, e_{j}\right)=\lVert\boldsymbol{h}_{e_{i}}^{M u l}-\boldsymbol{h}_{e_{j}}^{M u l}\rVert_{1}
$$
Experiments
详细的实验参数设置请参考原论文.
Baselines
由于实体对齐现在还处于没有统一的阶段, 有一些研究认为数据集信息不足, 尝试引入额外信息, 所以这会导致不公平的比较. 作者基于现在所使用的数据, 将其分为三类:
- Basic: 只使用原始数据.
- Semi - supervised: 引入半监督生成额外的结构化数据.
- Textual: 除了结构化数据, 引入了实体名作为额外的输入特征.
作者对RREA也制作了符合三类标准的三种版本, 以做公平比较.
Main Results
RREA vs. Basic and Semi-supervised Methods
与前两种模型比较结果如下:
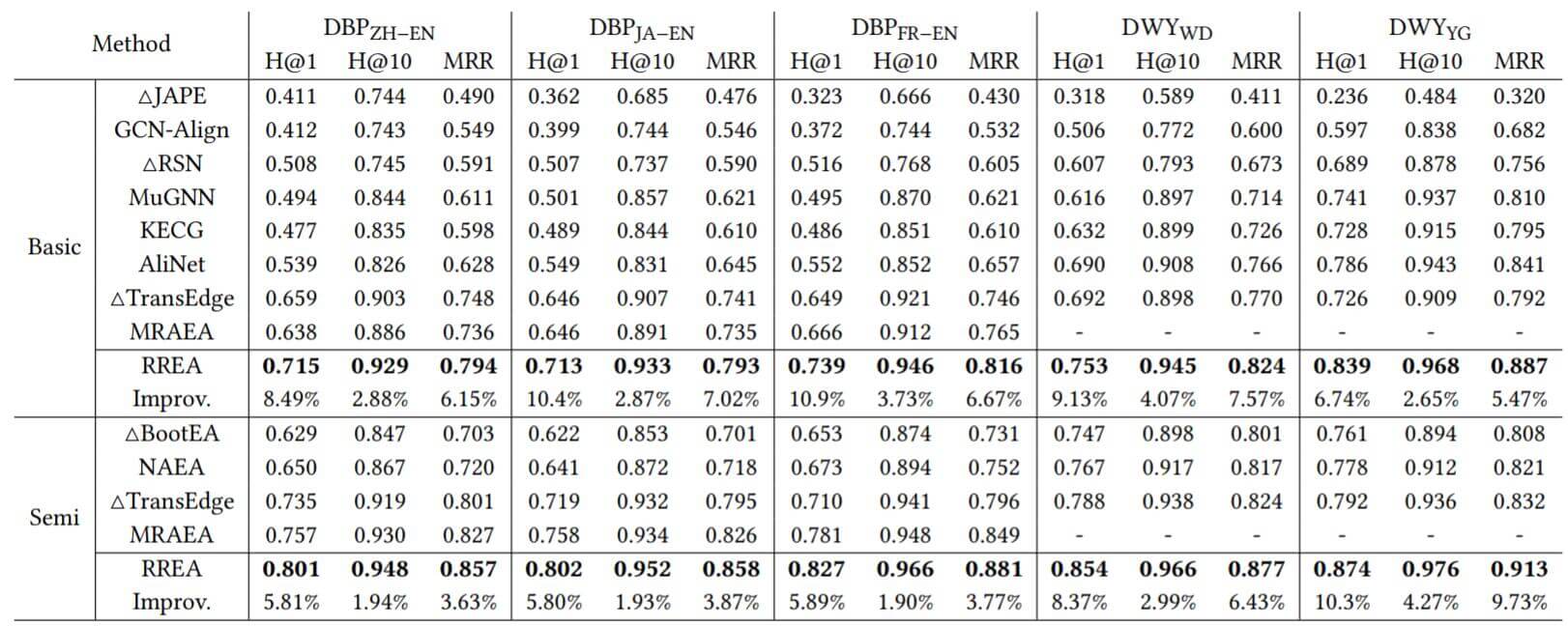
在Hits@1上提升非常明显, 可以说作者的方法有效性得到了验证. 在Hits@10上提升不是很多, 主要的提升都集中在Hits@1上, 说明RREA能够更精确的挑选出合适的实体对. 主要是因为关系反射变换为实体构建了特定关系的嵌入, 能更好的捕获信息.
RREA vs. Textual Methods
与引入实体名的方法相比, 结果如下:
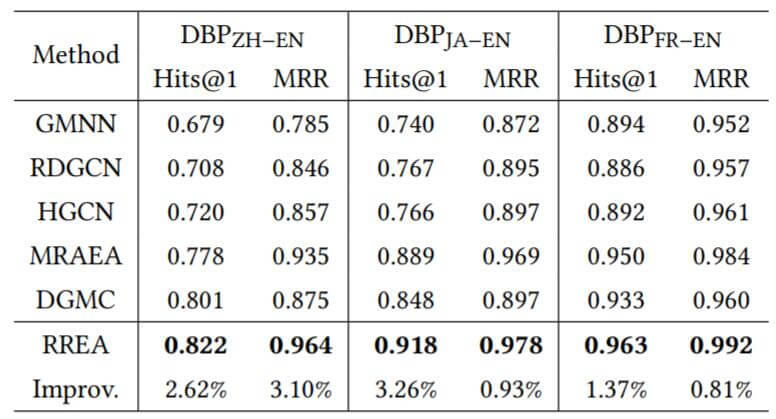
作者将提升归功于使用了MRAEA提出的无监督文本框架.
Ablation Study
消融实验结果如下:
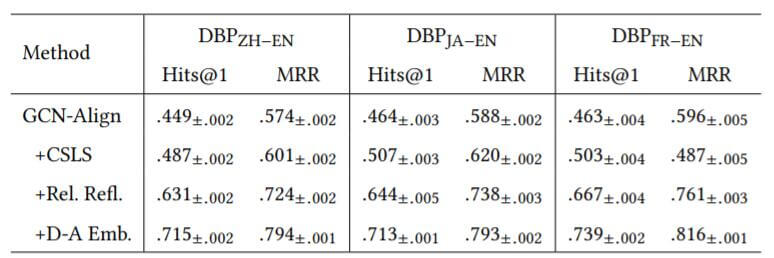
在模型中加入关系反射聚合和多重Embedding对模型提升都比较大, 引入了不同的信息.
Robustness Analysis
Robustness on Pre - aligned Ratio
作者希望能在低资源下表现良好, 因此在DBP15K中比较了三种基于GNN模型在不同数据量下的性能:
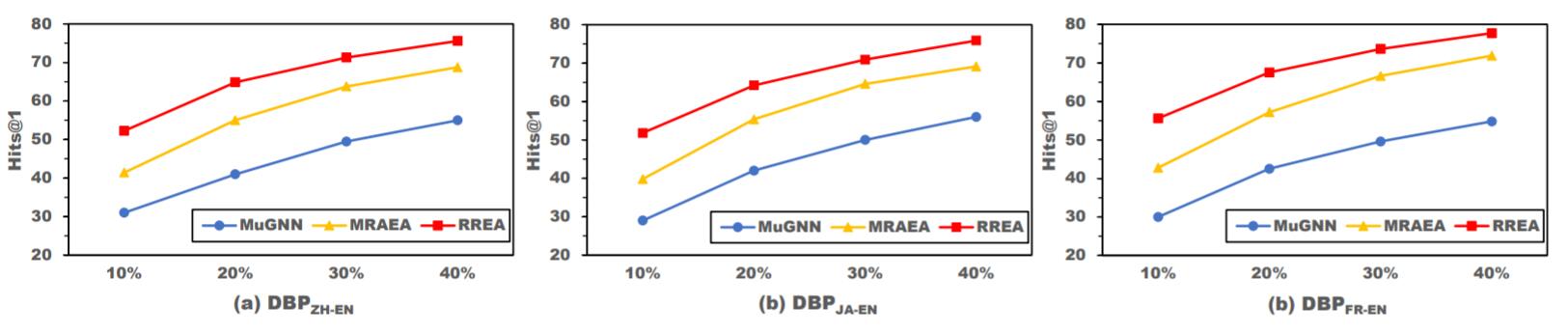
RREA全面领先.
Robustness on Hyper-parameter
为了探究RREA对超参数的鲁棒性, 作者在DBP15K上, 探究了RREA的超参数设置所带来的影响:
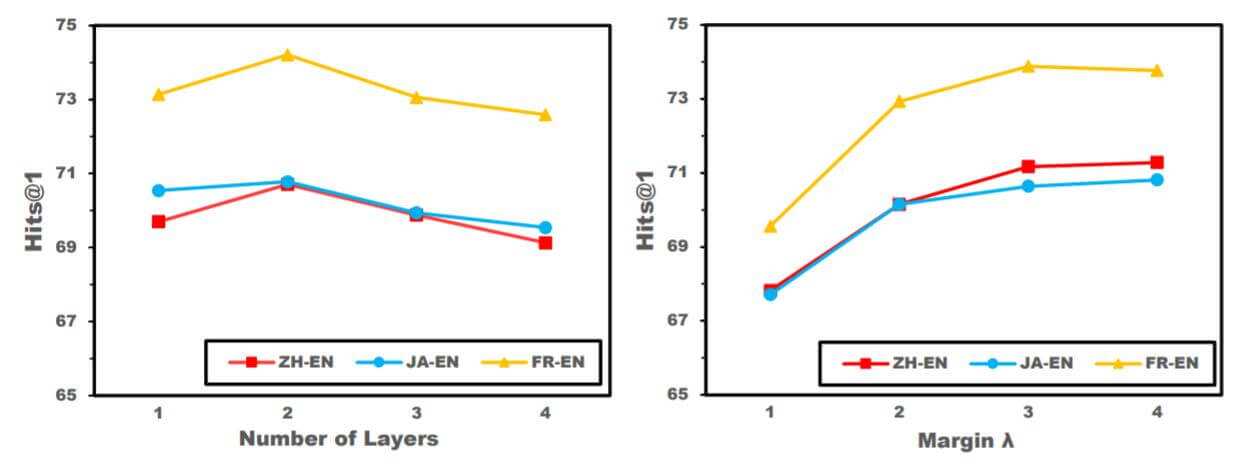
无论是GNN层数还是间隔$\lambda$, 作者认为对模型的影响都比较有限, 模型随超参变化相对比较稳定.
Summary
作者基于两个反直觉的现象, 提出了一种统一的实体对齐框架. 并强调了变换矩阵正交的重要性.
依据对两个问题的解释, 作者设计了一种能够解决反直觉问题的关系反射变换操作, 并提出了以此为基础的新方法RREA, 通过实验证明, 作者提出的方法在多种方法中属于优越的方法, 并且提升非常大.

