本文前置知识:

• Self - Attention
• BERT

2020.11.17: 解决了标签泄露的疑惑.

2021.04.09: 修正可视化实验的描述.

CoKE: Contextualized Knowledge Graph Embedding

本文是论文CoKE: Contextualized Knowledge Graph Embedding 的阅读笔记和个人理解.

Basic Idea

作者指出, 在先前的Embedding方法都是静态的, 忽略了实体和关系在不同图之间的上下文所对应的真正含义. 在不同的上下文中, 实体和关系的含义经常是不同的, 例如下图:

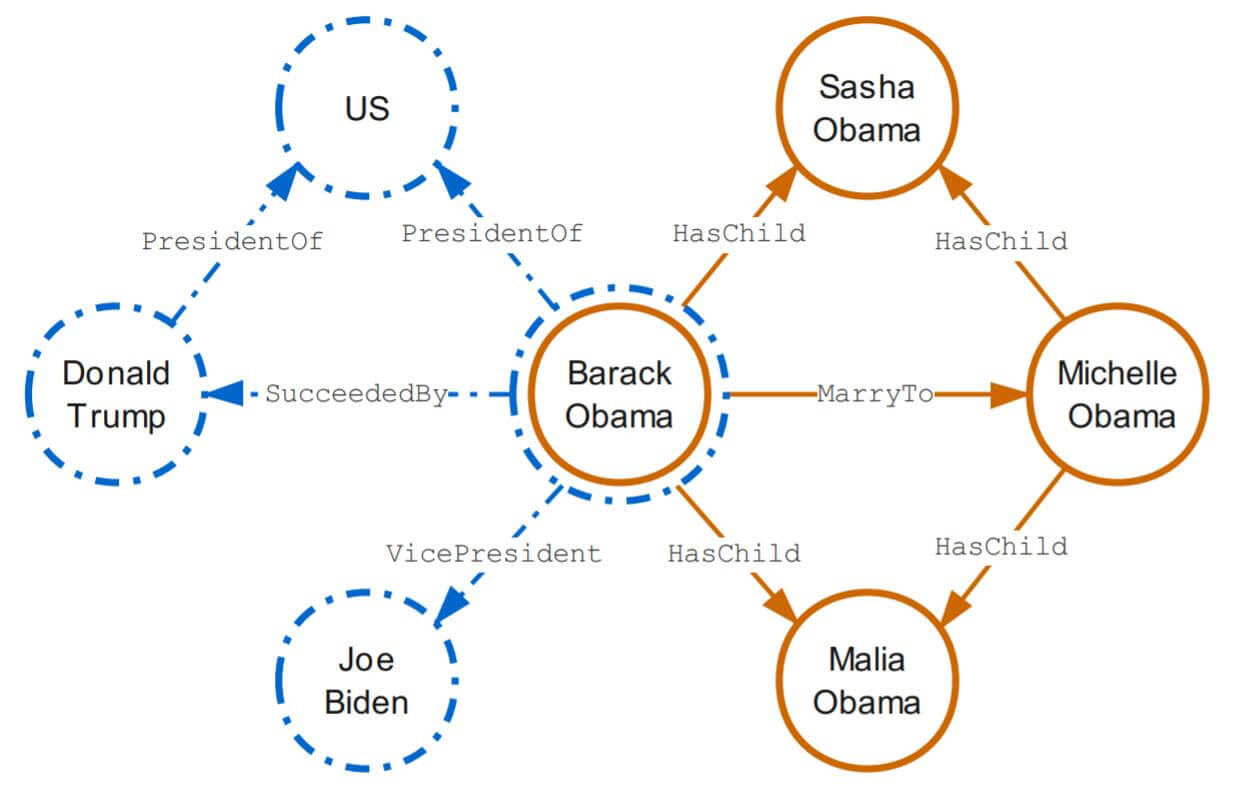
假设有两个子图, 代表政治关系的子图(左侧蓝色)和代表家庭关系子图(右侧橘色), 它们都指向同一个实体Barack Obama, 在不同子图中它们所代表的表示应该是不同的, 因为在政治和家庭领域中, Barack Obama应该具有不同的含义, 因此Embedding需要在不同语境中被动态表示. 必须根据上下文语义信息来判断应该采取怎样的表示. 相比于静态表示法, 结合上下文语义信息的表示法有更丰富而灵活的Embedding.

除此外还有一个重要原因, 作者发现实体和关系很少孤立出现, 它们更多的出现伴随丰富的上下文, 甚至以边, 路径, 子图的方式出现, 这就为利用上下文提供了极大地便利.

CoKE(Contextualized Knowledge Graph Embedding)的设计初衷便是一种结合语境的动态知识表示法.

CoKE

Problem Formulation

对于Knowledge Graph中给定的三元组结构$(s, r, o)$, 两个实体之间可能在给定的上下文中对应着两种情况:

• Edge:$s \rightarrow r \rightarrow o$, 即实体到实体只经过一跳, 用一种关系的边就能表示, 这是一种在知识图谱中最基本的方式. 例如$\text{BarackObama}\rightarrow\text{HasChild}\rightarrow\text{SashaObama}$.
• Path: $s \rightarrow r_{1} \rightarrow \cdots \rightarrow r_{k} \rightarrow o$, 即实体到实体需要用一系列关系构成的路径来表示, 由于包含了多跳信息, 这种表示往往伴随着更强的推理性. 例如$\text{BarackObama}\rightarrow\text{HasChild}\stackrel { (\text {Sasha}) }\rightarrow\text {LivesIn} \stackrel { \text {(US)} } \rightarrow\text{OffcialLanguage}\rightarrow\text{English}$.

CoKE的目标就是根据丰富的图结构上下文学习到实体和关系的动态自适应性表示.

Model Architecture

CoKE也采用了现在大家一致认为表现最好的Transformer Encoder(BERT) 架构完成Embedding. 其实模型的结构非常简单, 就是Transformer Encoder.

对于给定的输入序列$X=\left(x_{1}, x_{2}, \cdots, x_{n}\right)$, 在输入到Transformer Encoder前, 只需要对Token Emedding额外加上位置编码:
$$
\mathbf{h}_{i}^{0}=\mathbf{x}_{i}^{\mathrm{ele}}+\mathbf{x}_{i}^{\mathrm{pos}}
$$
需要注意的是, 这里没有对Entity和Relation的Embedding加以区分, 直接统一使用Word Embedding.

然后就对Transformer Encoder进行堆叠:
$$
\mathbf{h}_{i}^{\ell}=\text { Transformer }\left(\mathbf{h}_{i}^{\ell-1}\right), \quad \ell=1,2, \cdots ,L
$$
其中$\ell$ 代表Transformer的堆叠层数. 论文这里还吹了一波Transformer的双向捕捉上下文能力和其他优点等等. 通过多层堆叠处理后, 得到的表示$\left\{\mathbf{h}_{i}^{L}\right\}_{i=1}^{n}$ 是对输入自适应的.

Training

CoKE也用给Token打[Mask]的方式训练模型, 作者设计了一种给出子图上下文情况下的实体预测任务.

但是与Masked Language Model的Mask方式不同, 并不是对Sequence 随机Mask, 而是只对边(路径)中的实体进行Mask, 这样每次预测的任务类似于问答的任务. 并且这样还有一个好处, 在执行很多下游任务(例如实体链接, 路径查询问答)时, 这种方式能够完全的避免BERT遇到的Train - Test discripency.

Double Entity Mask

Double Entity Mask这个名字是我自己起的, 因为它分别Mask了两个不同的实体并创建了两个不同的实例.

针对我们在Problem Formulation中提到的, 在KG中对于给定的两个实体可能有两种情况, 分别是边和路径. 边可以看做是一种特殊的路径, 所以作者采用相同策略对它们进行Mask, 虽然形式上没有区别, 但实际上对模型有着不同的影响.

• 对于边$s \rightarrow r \rightarrow o$, 将产生两个实例, 分别是$? \rightarrow r \rightarrow o$ 和 $s \rightarrow r \rightarrow ?$. 要把实体预测出来, 这样的问题是在问答任务中的单跳问题. 例如$\text{BarackObama}\rightarrow\text{HasChild}\rightarrow?$, 就是在询问”Who is the child of Barack Obama?“.
• 对于路径$s \rightarrow r_{1} \rightarrow \cdots \rightarrow r_{k} \rightarrow o$, 也映射成两个实例, 分别预测头实体$s$ 和尾实体$o$. 它可以被看做是问答任务中的多跳问题. 例如$\text{BarackObama}\rightarrow\text{HasChild}\rightarrow\text {LivesIn} \rightarrow\text{OffcialLanguage}\rightarrow?$, 就是在询问”What is the official language of the country where Barack Obama’s child lives in?“.

将上面二者统一, 对于给定的输入序列$X=\left(x_{1}, x_{2}, \cdots, x_{n}\right)$, 创建两个训练实例, 一个用[MASK] 替换掉$x_1$ 来让模型预测头实体$s$, 与之相对的另一个用[MASK] 替换$x_n$, 让模型预测尾实体$o$. 然后将替换后的序列加上位置编码, 一股脑放进Transformer Encoder, 最后得到最终隐态$\mathbf{h}_{1}^{L}$ 和$\mathbf{h}_{n}^{L}$, 然后用它来预测被Mask的实体.

我之前以为这样会产生标签泄露, 实际上并不会产生标签泄露. 假设原三元组是$(h, r, t)$, 那么CoKE产生的实例是$(?, r, t)$ 和$(h, r, ?)$. 这时模型预测的分别是头实体和尾实体在相同关系下的概率分布.

与WN18和WN18RR的关系不一样, WN18RR是在WN18的基础上, 在训练集去除类似于$(t, r^{-1}, h)$ 这样的三元组. 也就是说在WN18中存在$(h, r, ?)$ 和$(t, r^{-1}, ?)$ 如果模型对顺逆关系做关联, 逆关系能直接泄露出另一端的实体嵌入.

Classification

和BERT一致, 在最后分类的时候用前馈神经网络和Softmax来做实体的预测:
$$
\begin{array}{l}
\mathbf{z}_{1}=\text { Feedforward }\left(\mathbf{h}_{1}^{L}\right), \mathbf{z}_{n}=\text { Feedforward }\left(\mathbf{h}_{n}^{L}\right) \\
\mathbf{p}_{1}=\operatorname{softmax}\left(\mathbf{E}^{\mathrm{ele}} \mathbf{z}_{1}\right), \mathbf{p}_{n}=\operatorname{softmax}\left(\mathbf{E}^{\mathrm{ele}} \mathbf{z}_{n}\right)
\end{array}
$$
其中$\mathbf{E}^{\mathrm{ele}}$ 是和实体Embedding共享权重的分类权重矩阵.

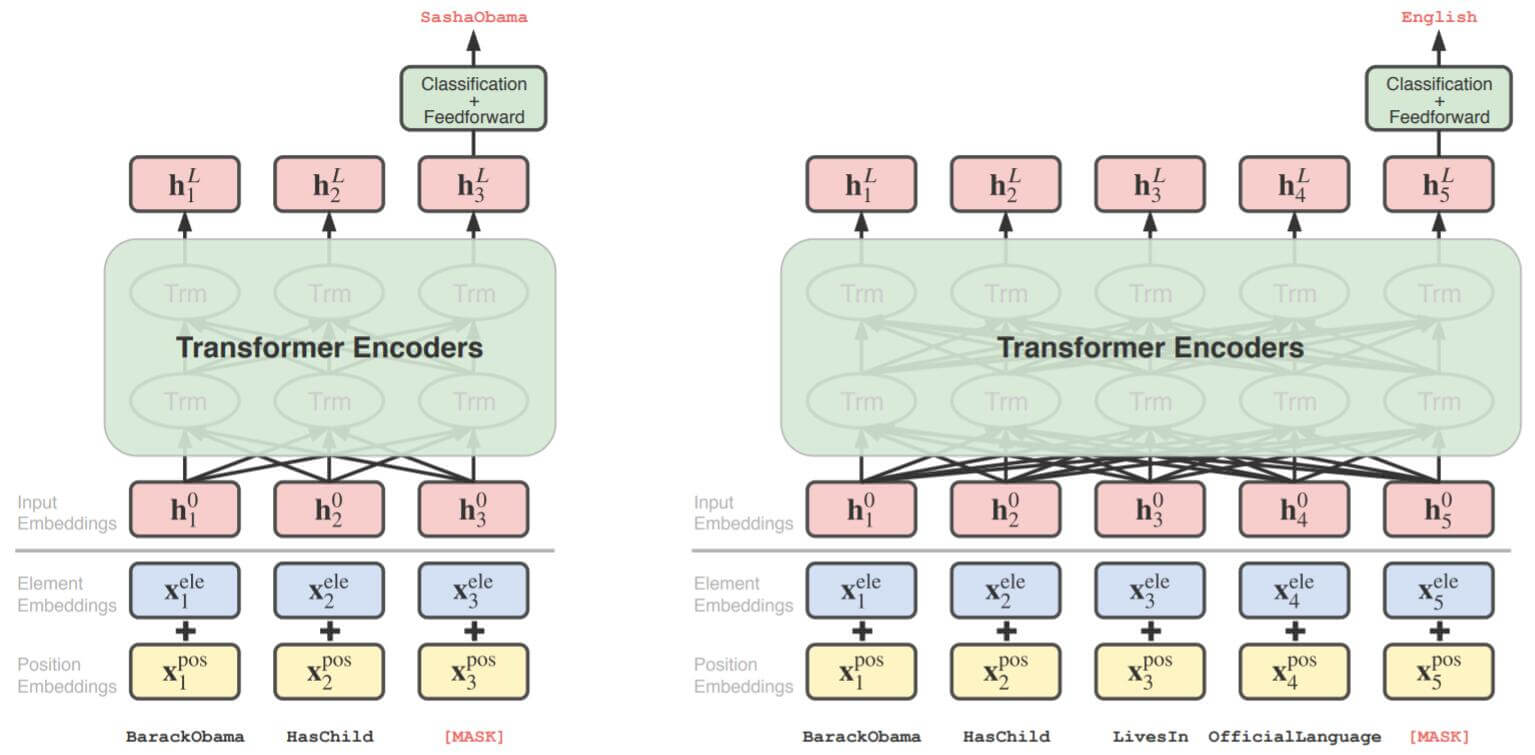
模型的概览图如下:

左图是对边的Mask, 右图是对关系的Mask. 它们都是通过Transformer Encoder最后时刻的隐态来确定被Mask掉的目标实体.

Loss Function

因为以分类为目标, 所以用交叉熵为损失函数;
$$
\mathcal{L}(X)=-\sum_{t} y_{t} \log p_{t}
$$
训练时还使用了标签平滑, 设定实体标签所对应的$y_t=\epsilon$, 其他实体$y_{t}=\frac{1-\epsilon}{V-1}$.

Experiment

Link Prediction

链接预测上使用了FB15k, WN18和剔除包含反关系的FB15k-237, WN18RR.

CoKE只允许最大输入序列长度为3, 即只使用三元组, 不使用上下文. 结果直接使用了filtered setting, 对头实体和尾实体分别Mask再预测, 用MRR, H@n来测试性能. 详细的参数设置和训练Trick请见原论文.

Filtered setting最早出现在TransE的论文中, 为了避免在替换实体后三元组仍然正确, 从而将正确的答案判为错误, 看低模型性能. 避免的方法是从替换后的实体中剔除在训练集, 验证集, 测试集中已经出现过的三元组.

Main Result

FB15k, WN18:

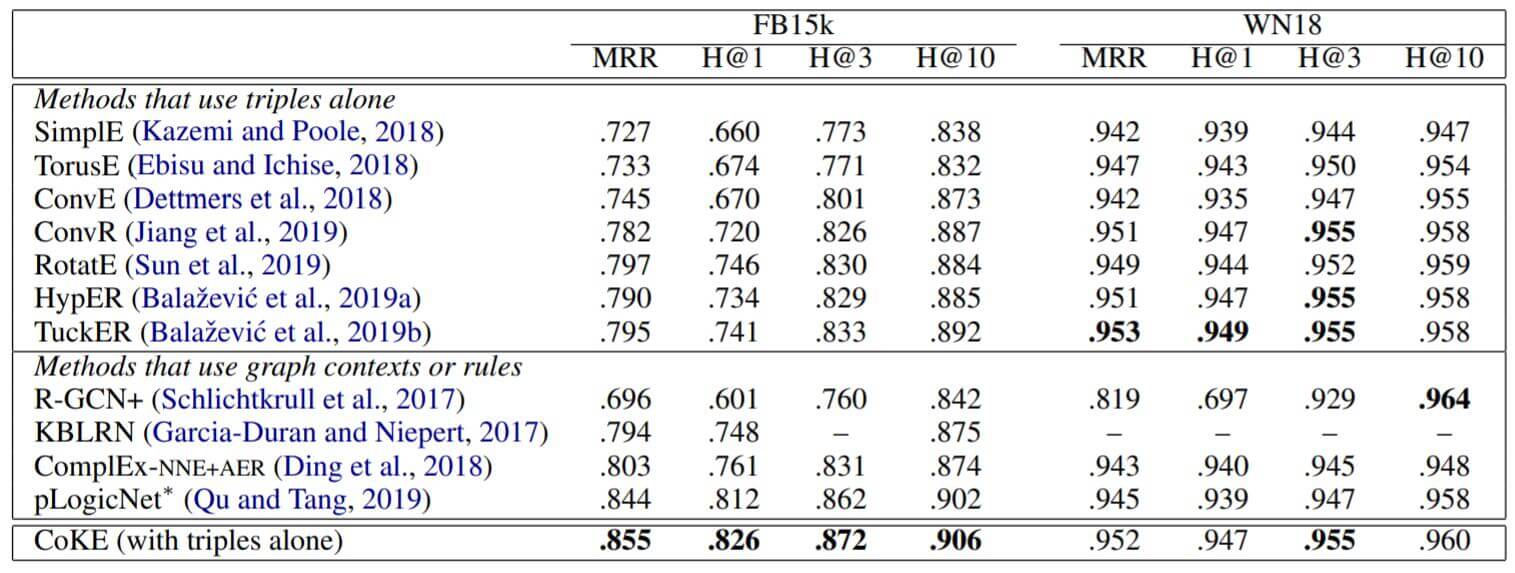
上面一组是没有使用上下文的Embedding方法, 下面一组是结合上下文或路径的方法. CoKE在这里只使用了三元组, 应该从属于第一组. 在FB15k上表现良好, WN18上与最佳结果差距不大.

FB15k-237, WN18RR:

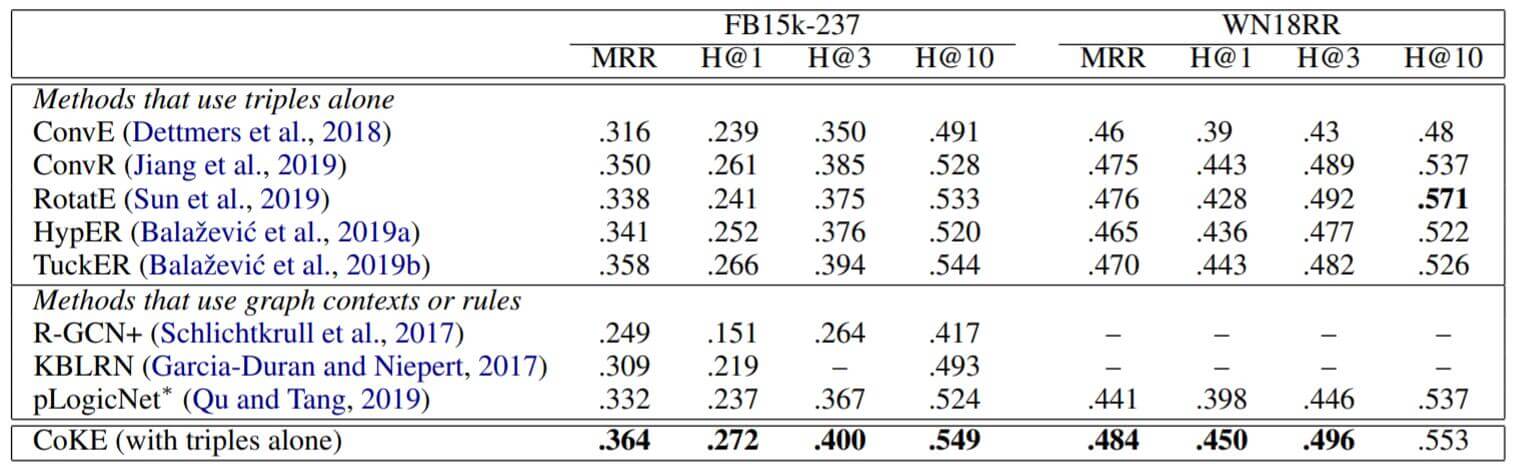
仍然表现不错, 除了WN18RR上与RotatE差距较大.

这组只使用三元组的CoKE证明它在单跳推理上的表现很不错.

Parameter Efficiency

作者还在这比较了一下CoKE的参数效率, 当然这是建立在预测效果之上:

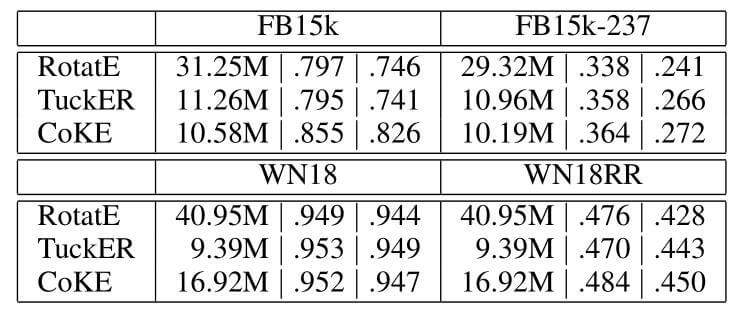
我觉得都已经上Transformer了, 就别再考虑啥参数效率了吧, 很大一个原因是它只使用了256维的Embedding, 并且每层只用了4个头.

Path Query Answering

这个任务与两实体间需要多跳, 且有一个实体被Mask掉情况相同. 作者使用Random Walk从WordNet和FreeBase生成数据. 最多通过连续$k$ 跳从头实体$s$ 到达尾实体$o$. 在本任务中, 限制输入序列长为7, 即两实体间最多有5跳.

Main Results

作者将正确的答案$o$ 和不正确的答案$\mathcal{N}$ 的概率分布按降序排序, 并计算在$o$ 后不正确的答案占结果的总比例, 记为MQ, 范围是0到1, 1为最佳. 是按结果如下:

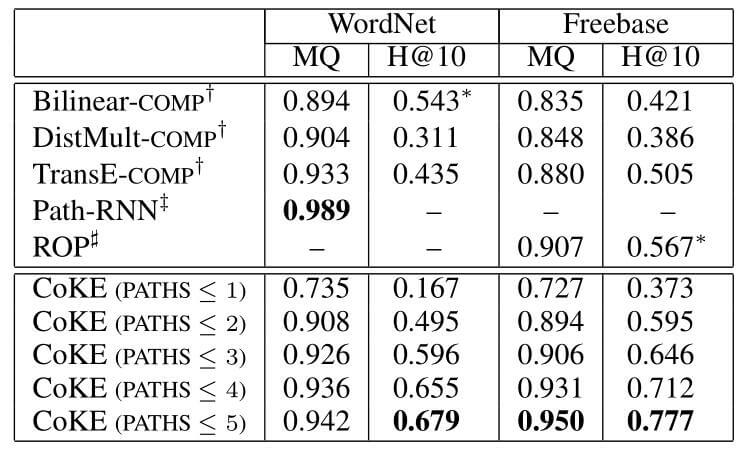
关于问答相关的内容还不是很了解. 但能看到随着Path长度的增加, 性能逐渐提升. 到$k\leq3$ 时, 性能就已经全面领先于作者列出的方法了. 在本任务中CoKE作者证明了具有多跳推理能力.

Further Analysis

作者想检测CoKE是否不但拥有多跳推理能力, 还同时经过多跳推理而强化了单跳推理能力. 作者设计了一个实验, 在训练CoKE时使用不同路径长的数据, 但在测试时仅让CoKE预测三元组(长度为1). 结果如下:

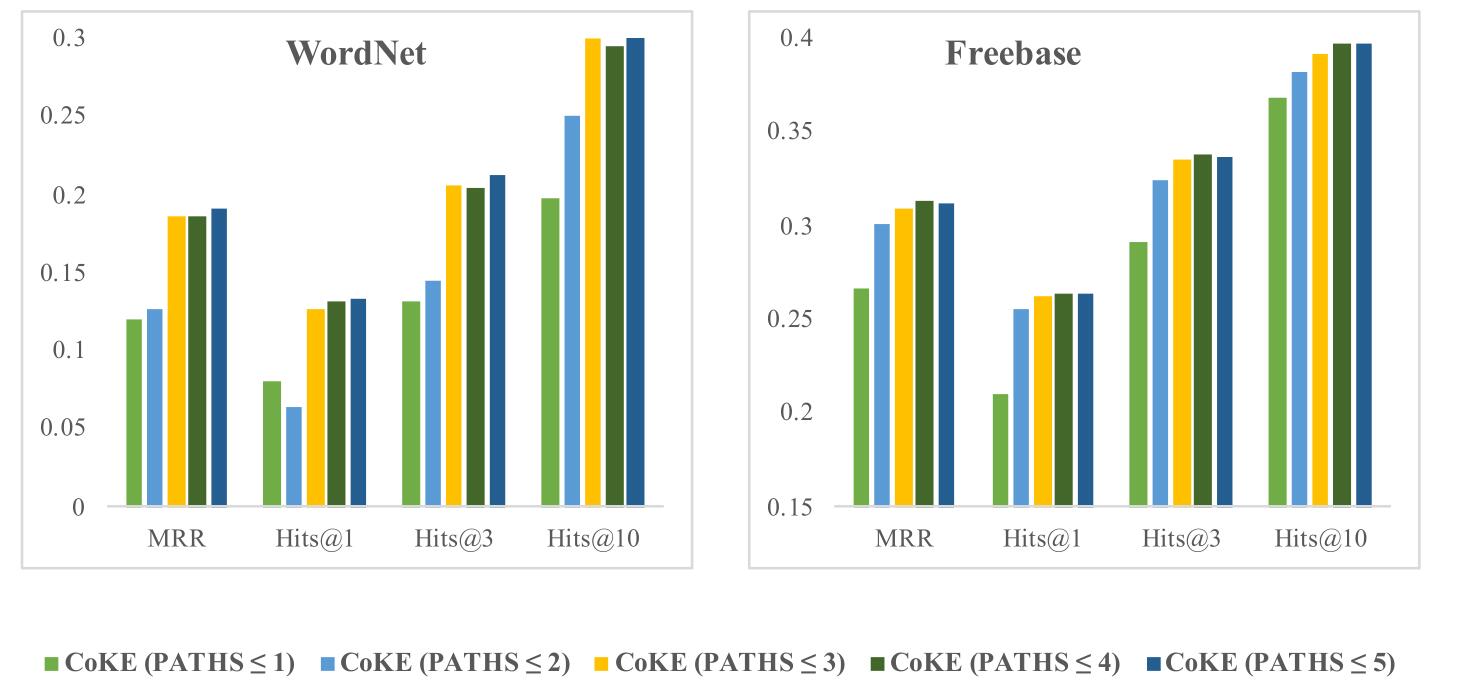
结果显示, CoKE随着训练时可使用的数据路径长的增加, 单跳推理能力也会增加. 证明了多跳推理的训练有利于单跳推理能力的提升.

Visual Illustration

作者通过T - SNE探究了CoKE对上下文语境利用的情况.

从FB15k中以实体TheKingsSpeech为例, 将所有三元组收集起来. 将在不同语境下的TheKingsSpeech Mask掉(无论是头还是尾), 然后用已经训练好的CoKE获取它的Final Hidden State $\mathbf{h}_n^L$, 再用T - SNE降维可视化.

先看左图, TheKingsSpeech的表示形式在不同的关系之间表示是不同的, 大概有几种不同的关系. 作者不同关系使用不同颜色区分. 例如award winning work/award winner 和award nominated work/award nominee具有几乎相同的表示, 都聚在左上角. 这说明CoKE具有了结合上下文信息的能力.

另外, 对于顺关系$(s, r, o)$的逆关系$\left(o, r^{-1}, s\right)$, 例如film/genre和film genre/films in this genre, 因为TheKingsSpeech在顺逆关系中从属于不同的头尾位置, 但是它们居然获得了相同的表示, 说明CoKE对逆关系能够很好的识别.

右图也是CoKE对顺逆关系学习的探究, 这回作者直接将每组互逆关系对用相同的颜色和正三角倒三角表示, 结果显示几乎所有相同颜色的三角都聚到了一起. 但右侧有两堆不同颜色的三角聚到了一起, 分别是JoelCoen和EthanCoen, 这两人被称为科恩兄弟, 共同创作. 这表明了CoKE对关系的区分粒度.

Summary

CoKE的思路其实很不错, 考虑到了已出现两个实体之间的单跳和多跳关系, 采用了目前效果最好的Transformer Encoder(BERT)作为特征抽取器.

同时该思考, 如果有某些暗含的背景因素没有出现在两实体中, 是否有可能对这两实体或关系的表示产生影响? 比如我们得到的路径是$A \rightarrow r_{1} \rightarrow \cdots \rightarrow r_{k} \rightarrow B$, 但是有某个隐含的背景条件或是实体有$C\rightarrow A$, 能对$A, B$的表示产生影响, 这种情况应该如何处理? 其实已经有方法给出了这个问题的解决方案.

值得一提的是, 作者在探究实验上的设计是很有意思的, 首先是想到了证明多跳能强化单跳的推理能力, 其次就是使用T - SNE来可视化探究CoKE对上下文的利用和识别能力.

最后, 如果对我提出的思考感兴趣, 或是对结合上下文Embedding的相关内容感兴趣, 欢迎阅读我写的CoLAKE: Contextualized Language and Knowledge Embedding, 我认为CoLAKE比CoKE要进步了不少.