Generative Adversarial Zero-Shot Relational Learning for Knowledge Graphs
本文是论文Generative Adversarial Zero-Shot Relational Learning for Knowledge Graphs的阅读笔记和个人理解. 本论文涉及到大量关于GAN的内容, 我对GAN还不是很熟悉, 在论文中具体的内容也不展开讲了, 我会放在推荐阅读中. 其中涉及到的地方如果有错误欢迎指出.
Basic Idea
作者指出, 即使是现在的大规模知识图谱, 仍然有可能无法满足日益增长的扩展需求.
对于新加入的关系, 经典的KGE算法无法应对新加入的关系. 而获取人为标注的数据是非常困难的, 因此作者希望能通过Zero - Shot Learning来缓解数据缺失的问题. 更具体点, 从关系的文本中学习它们的语义特征, 来增强在没有见过任何样本的情况下对没见过的关系的认知能力.
作者提出了一种KGE范式, 能够把任意的KGE方法应用于此.
Convert into Knowledge Transfer Problem
作者将Zero Shot Learning转化为一个知识迁移问题, 作者将关注如何只用文本描述生成没见过的关系嵌入, 这样, 只要经过训练, 模型能对任意关系在不进行Fine Tune的情况下生成嵌入. 通过关系嵌入, 能够对没有见过的关系通过余弦相似度简单的识别.
最首要的问题就是将文本语义空间的信息迁移到KG语义空间, 对此作者采用GAN来做知识迁移, 作者提出的架构如下:

对于模型已经见过的文本, 训练一个生成器(Generator), 能够从文本中生成相应的Fake Relation Embedding, 再针对该关系中所涉及到的头尾实体使用某种方法编码成Real Relation Embedding. 将真与假的Relation Embedding交替输入判别器(Discriminator), 让它来判断Relation Embedding到底是真的还是假的.
当Generator生成的数据能够以假乱真时, 生成器所生成的Relation Embedding就能直接近似的当做是未见过的关系的Relation Embedding, 在Link Prediction任务中, 便能轻松应对未见过的关系.
Zero - Shot Learning in KG
有必要稍微说一下Zero - Shot Learning在Link Prediction的设定.
对于一个查询关系三元组$\left\{\left(e_{1}, r, e_{2}\right)\right\}$, 给定头实体和关系元组$(e_1, r)$, 假设其应该对应的候选尾实体$e_2^\prime \in C_{\left(e_{1}, r\right)}$, 其真正的尾实体是$e_2$. 模型应该能将真正尾实体$e_2$ 排在最高, 而其余候选集合的实体$e_2^{\prime}$ 应该排在后面.
在Zero - Shot Learning的设置下, 还应该有见过的关系集$R_{s}=\left\{r_{s}\right\}$ 和没有见过的关系集$R_{u}=\left\{r_{u}\right\}$, 显然$R_{s} \cap R_{u}=\emptyset$.
对于训练集, 所有关系都是见过的, 即:
$$
D_{s}=\left\{\left(e_{1}, r_{s}, e_{2}, C_{\left(e_{1}, r_{s}\right)}\right) \mid e_{1} \in E, r_{s} \in R_{s}, e_{2} \in E\right\}
$$
在测试集中, 所有关系都是没有见过的, 即:
$$
D_{u}=\left\{\left(e_{1}, r_{u}, e_{2}, C_{\left(e_{1}, r_{u}\right)}\right) \mid e_{1} \in E, r_{u} \in R_{u}, e_{2} \in E\right\}
$$
出于可行性, 作者将所有实体设置为闭集, 即测试集中出现的所有实体均在训练集中见过.
Model for Zero-Shot KG Relational Learning
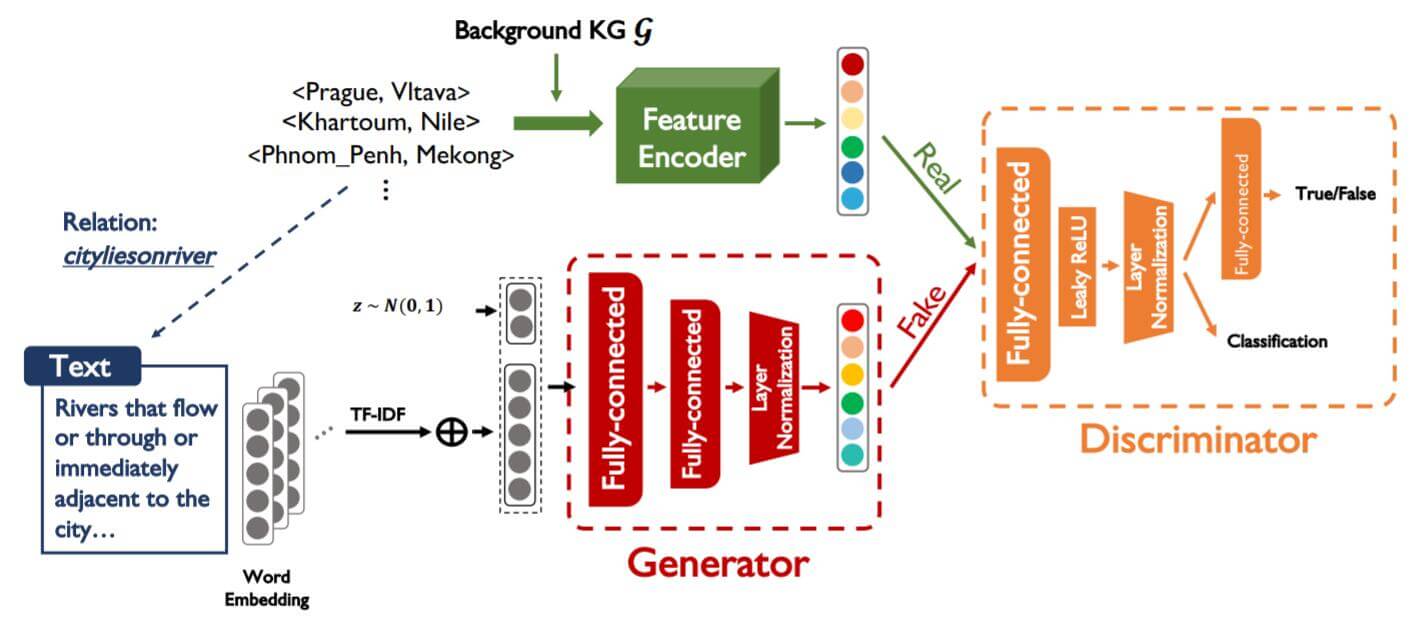
该图在后文中讲解关于GAN的部分会再次出现.
作者提出的方法中, 核心问题是如何设计一种条件生成模型, 去学习从文本中生成高质量的关系嵌入. 在作者的框架中, 主要设计了三个组件:
- Feature Encoder: 仅通过实体生成真实的Relation Embedding.
- Generator: 在文本表示下生成合理的Relation Embedding.
- Discriminator: 判断数据的来源真假, 并识别关系类别.
Feature Encoder
对于没见过的关系, 普通KGE方法是无法取得其Embedding的.
Feature Encoder使用的Embedding可以是任意KGE模型得来的Embedding, 这也就是为什么作者说这是一种Zero - Shot的使用范式, 能够应用于任何的KGE方法.
Feature Encoder应该是在GAN训练前预先训练好的, 训练生成器和判别器时, 其参数应该不变.
Network Architecture
出于大规模KG的复杂度, 考虑到实验的可行性, 对于每个实体对中的$e$, 作者只考虑到它们的一阶邻居$\mathcal{N}_{e}$:
$$
\mathcal{N}_{e}=\left\{\left(r^{n}, e^{n}\right) \mid\left(e, r^{n}, e^{n}\right) \in \mathcal{G}\right\}
$$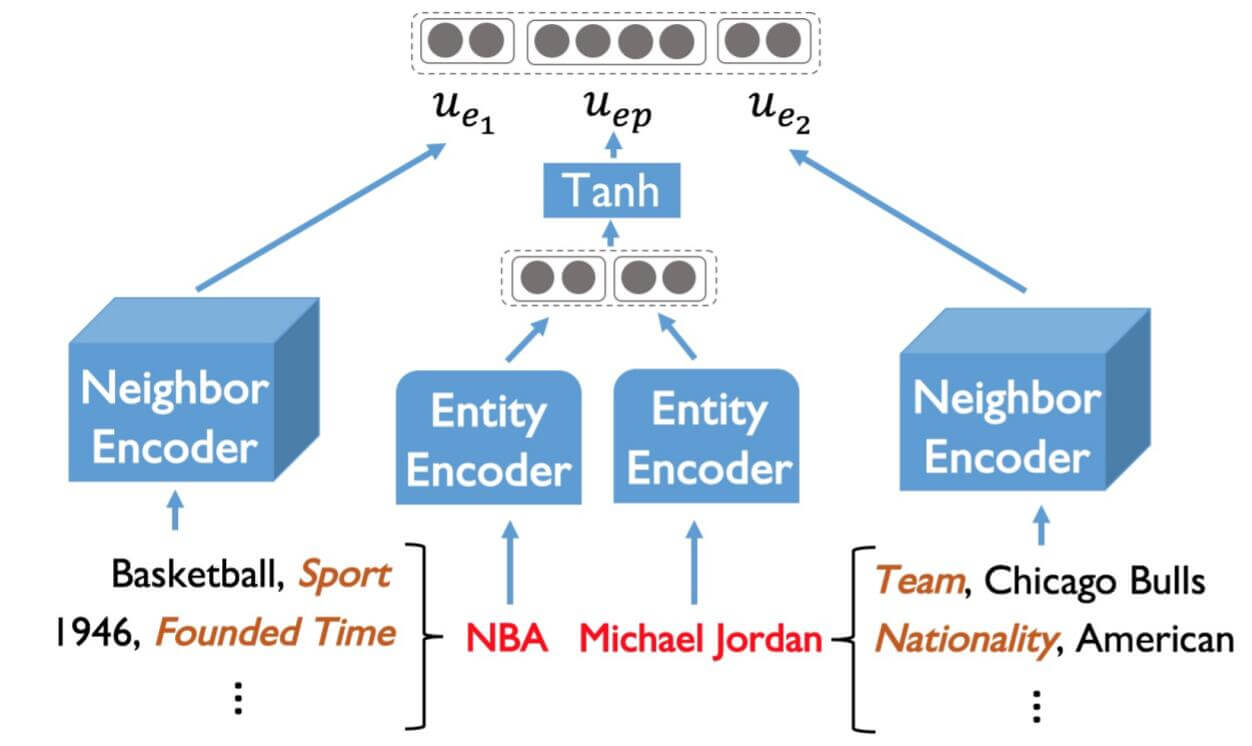
假设在原来的KGE模型中, 给出的邻居关系和实体Look Up Table Embedding分别为$v_{r^{n}}, v_{e^{n}}$, 其嵌入维度为$d$, 那么该实体$e$ 一阶邻居的所有信息$u_e$ 能被表示为:
$$
\begin{array}{l}
f_{1}\left(v_{r^{n}}, v_{e^{n}}\right)=W_{1}\left(v_{r^{n}} \oplus v_{e^{n}}\right)+b_{1} \\
u_{e}=\sigma\left(\frac{1}{\left|\mathcal{N}_{e}\right|} \sum_{\left(r^{n}, e^{n}\right) \in \mathcal{N}_{e}} f_{1}\left(v_{r^{n}}, v_{e^{n}}\right)\right)
\end{array}
$$
其中的$\sigma$ 是$\operatorname{tanh}$. $\oplus$ 代表Concat操作. 出于可行性, 作者限制了邻居的采样个数.
将该实体对应在图中, 这个操作其实本质上就是图聚合.
对于实体对$(e_1, e_2)$ 中的两个实体本身也需要被编码, 只考虑用前馈神经网络简单的进行编码即可:
$$
\begin{array}{l}
f_{2}\left(v_{e}\right)=W_{2}\left(v_{e}\right)+b_{2} \\
u_{e p}=\sigma\left(f_{2}\left(v_{e_{1}}\right) \oplus f_{2}\left(v_{e_{2}}\right)\right)
\end{array}
$$
最后将计算出的实体对编码和实体对中实体的邻居编码Concat起来, 得到$e_1, e_2$ 之间的关系表示$x_{(e_1, e_2)}$:
$$
x_{\left(e_{1}, e_{2}\right)}=u_{e_{1}} \oplus u_{e p} \oplus u_{e_{2}}
$$
上述过程中$W_1 \in R^{d \times 2d}, W_2 \in R^{d \times d}, b_1,b_2 \in R^d$ 均为可以学习的参数.
Pretrained Strategy
作者指出, 预训练的关键是学习到了簇状结构数据的分布, 一般具有簇内的高相似度和簇外的低相似度. 对于每个关系$r_s$, 在每个Training Step中, 采样以下三种三元组:
- $\left\{e_{1}^{\star}, r_{s}, e_{2}^{\star}\right\}$: 直接无差别的随机从KG中选择与$r_s$ 相关的三元组, 称为参考三元组.
- $\left\{e_{1}^{+}, r_{s}, e_{2}^{+}\right\}$: 从训练集中, 采样包含关系$r_s$ 的正例三元组.
- $\left\{e_{1}^{+}, r_{s}, e_{2}^{-}\right\}$: 从其余的训练集中, 做替换尾实体的负采样, 称为负例三元组.
通过Feature Encoder能生成参考三元组的真实关系表示$x_{(e_1^{\star}, e_2^{\star})}$, 然后分别计算参考三元组与正例负例三元组之间的余弦相似度:
$$
\begin{aligned}
score^+_\omega &=\operatorname{cosine}(x_{(e_1^{\star}, e_2^{\star})}, x_{(e_1^{+}, e_2^{+})}) \\
score^-_\omega &=\operatorname{cosine}(x_{(e_1^{\star}, e_2^{\star})}, x_{(e_1^{+}, e_2^{-})})
\end{aligned}
$$
那么最终目标就是最大化间隔:
$$
L_{\omega}=\max \left(0, \gamma+\operatorname{score}_{\omega}^{+}-\operatorname{score}_{\omega}^{-}\right)
$$
其中$\gamma$ 是间隔, $\omega$ 是模型中涉及到的所有可学习参数. 通过计算余弦相似度, Feature Encoder能尽可能的将实体之间的关系聚类, 从而生成到作者所说的簇状结构数据.
Generative Adversarial Model

Generator
生成器的作用是从嘈杂的文本$T_r$ 中生成伪造的Relation Embedding. 但因为文本中经常伴随着非常多的停止词之类的无意义词语, 所以作者简单的去除停止词和标点, 并使用TF - IDF来分配词语的权重. 词向量直接使用Word2Vec将词语转化为稠密向量. 在Sentence Level Modeling上, 作者使用无视语序的词袋模型对句子建模.
至于为什么作者没有在词向量上使用BERT, 在后文的实验中作者做了探究.
Generator在生成数据时, 一般都需要加入一些噪声. 在这里, 作者加入高斯随机噪声$z \in R^Z$, $z$ 是从高斯分布$N(0, 1)$ 中采样的来的向量.
作者将高斯噪声$z$ 和TF - IDF后的句向量Concat起来, 经过两个FC层和一个Layer Norm, 最后得到生成器$G$ 通过文本生成的Relation Embedding $\tilde{x}_{r}$, 即$\tilde{x}_{r} \leftarrow G_{\theta}\left(T_{r}, z\right)$, 其中$\theta$ 是参数.
对于GAN的训练方面, 为了避免模型崩溃并增强多样性(在推荐阅读中, 有解释GAN训练上出现的常见问题), 作者使用了WGAN中的Wasserstein Loss.
作者继续添加了分类损失, 其形式与Feature Encoder中使用的最大化间隔损失类似, 计算它分别与正例(在GAN训练时正例指$\tilde{x}_{r}$)和负例三元组之间的相似度, 但作者将簇中心$x_c^r$ 作为真实的关系表示:
$$
x_{c}^{r}=\frac{1}{N_{r}} \sum_{i=1}^{N_{r}} x_{\left(e_{1}, e_{2}\right)}^{i}
$$
其中$N_r$ 为涉及到关系$r_s$ 所有的三元组个数.
那么分类损失可以被写成:
$$
\begin{aligned}
score^+_\omega &=\operatorname{cosine}(x_{c}^r, \tilde x_r) \\
score^-_\omega &=\operatorname{cosine}(x_{c}^r, x_{(e_1^{+}, e_2^{-})}) \\
L_{cls}\left(G_{\theta}\left(T_{r}, z\right)\right)&=\max \left(0, \gamma+\operatorname{score}_{\omega}^{+}-\operatorname{score}_{\omega}^{-}\right)
\end{aligned}
$$
最后, 作者还添加了Visual Pivot Regularization, 用于增加类内的区别.
生成器的损失函数如下:
$$
L_{G_{\theta}}=-\mathbb{E}_{z \sim p_{z}}\left[D_{\phi}\left(G_{\theta}\left(T_{r}, z\right)\right)\right] +L_{c l s}\left(G_{\theta}\left(T_{r}, z\right)\right)+L_{P}
$$
第一项是Wasserstein Loss, 第二项是Classification Loss, 第三项是Visual Pivot Regularization.
Discriminator
判别器的作用是用于识别输入是否是伪造的. 生成器的结构比较简单, 只由一层使用Leaky ReLU的FC层, 接上Layer Norm组成, 最后结果分别用于判别真假和对关系分类, 损失函数如下:
$$
L_{D_{\phi}}=\mathbb{E}_{z \sim p_{z}}\left[D_{\phi}\left(G_{\theta}\left(T_{r}, z\right)\right)\right]-\mathbb{E}_{x \sim p_{\text {data}}}\left[D_{\phi}(x)\right]
+\frac{1}{2} L_{c l s}\left(G_{\theta}\left(T_{r}, z\right)\right)+\frac{1}{2} L_{c l s}(x)+L_{G P}
$$
第一二项仍然来自于Wasserstein Loss, 第三四项来源于分类, 分别对应着生成器的假数据$\tilde{x}_{r}$ 和Feature Encoder生成的真实数据$x_{(e_1, e_2)}$, 最后一项是梯度惩罚项.
GAN相关的细节还不太懂, 不瞎解释了.
GAN Training Process
在讲解完生成器和判别器后, 作者将GAN训练流程总结如下:

在GAN中, 通常采用多次更新判别器参数后只更新一次生成器的策略.
Predicting Unseen Relations
在训练完GAN后, 生成器对于一个没有见过的关系描述文本$T_{r_u}$ 应该能给出合理的Relation Embedding, 即$\tilde{x}_{r_u} \leftarrow G_{\theta}\left(T_{r_u}, z\right)$. 在已知$(e_1, r_u)$ 的情况下, 我们应该根据生成器所生成的$\tilde{x}_{r_u}$ 与Feature Encoder产生的$x_{(e_1, e_2)}$ 的余弦相似度来评估计排名:
$$
\operatorname{score}_{\left(e_{1}, r_{u}, e_{2}\right)}=\operatorname{cosine}\left(\tilde{x}_{r_u}, x_{(e_1, e_2)}\right)
$$
但生成器会为生成的数据添加噪声, 为了尽可能弱化随机造成的影响, 作者采用生成多组数据最后取平均的方法计算得分:
$$
\operatorname{score}_{\left(e_{1}, r_{u}, e_{2}\right)}=\frac{1}{N_{\text {test}}} \sum_{i=1}^{N_{\text {test}}} \text {score}_{\left(e_{1}, r_{u}, e_{2}\right)}^{i}
$$
即生成任意数量$N_{test}$ 的Relation Embedding$\left\{\tilde{x}_{r_{u}}^{i}\right\}_{i=1,2, \dots, N_{\text {test}}}$, 最后取平均余弦相似度作为真正的得分.
Experiments
在本节中, 详细的参数设置请参考原论文.
DataSet
作者发现没有可用的ZS数据集, 所以作者自己根据需要制作了两个数据集:
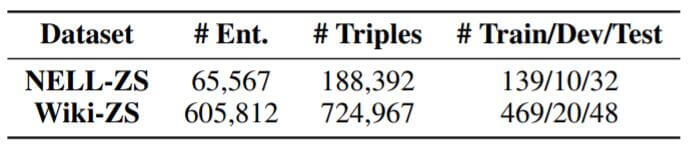
作者选取数据集的标准是, 满足大规模, 并含有关系文本描述.
Baselines
在非常普遍使用的KGE方法中, 它们基本不具备Zero - Shot的能力, 因为对于没有见过的关系, 在它们所存储的Embedding矩阵中是查询不到的, 所以作者用与Generator类似的方法为它们添加了Zero - Shot的能力: 使用一个与Generator类似的神经网络结构, 而不是直接为未知的关系生成随机的Relation Embedding. 在这个条件下, 模型能够直接根据文本信息生成未见过关系的Embedding, 然后继续结合它们原来的目标函数来调整Entity Embedding和与Generator类似的结构的参数.
例如, 在TransE中, Entity Embedding和Relation Embedding都是使用一个Look Up Table存储的:
$$
f_{\text {Trans} E}(\boldsymbol{h}, \boldsymbol{r}, \boldsymbol{t})=\left|v_{h}+v_{r}-v_{t}\right|_{1 / 2}
$$
在经过改造后, 它们的Relation Embedding不再通过Look Up Table给出, 而是通过类似生成器的结构$g$ 从文本$T_r$ 中生成:
$$
v_{r}=g\left(T_{r}\right)
$$
在对实体排名时, 也是按照它们原本的打分函数进行排名.
对于DisMult, ComplEx亦是如此. RESCAL都没有替换Relation Embedding的位置, 所以就不对它进行比较了.
Results
作者将改进后的Zero - Shot模型在自己制作的数据集NELL - ZS和Wiki - ZS上测试了它们Link Prediction的能力, 结果如下:
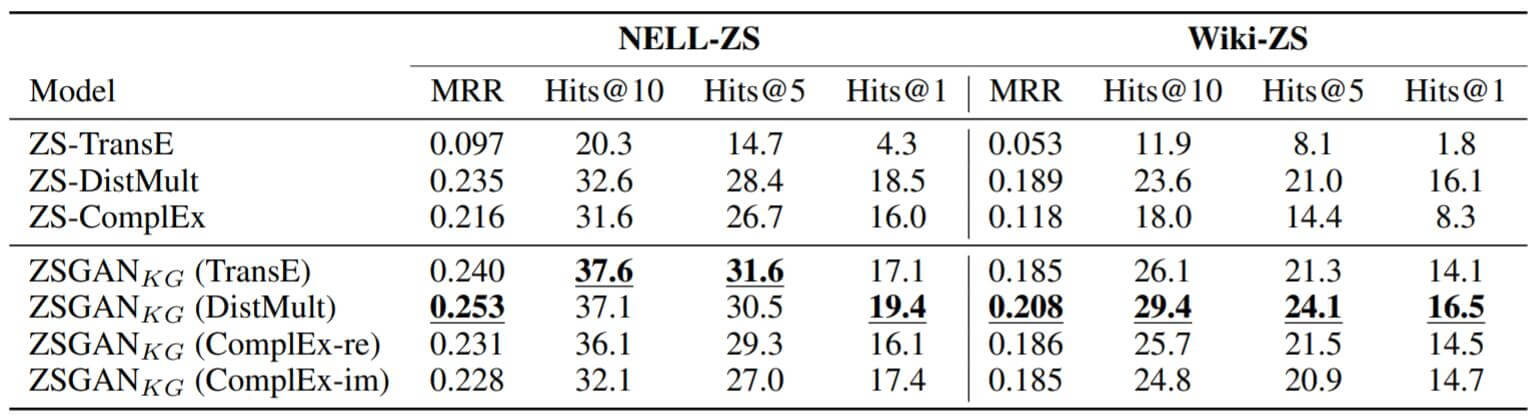
其中ZSGAN代表使用了GAN训练框架, 即在之前的基础上加入了判别器, 并引入GAN相关的训练损失.下划线代表该结果在ZSGAN中是最棒的.
能从结果中观察到, 所有使用ZSGAN的模型都比未使用GAN的Baseline效果要好, 并且在这些模型中, DisMult体现出更好的能力.
Analysis of Textual Representations
Text Descriptions Analysis
作者将自制的两个数据集中的关系文本描述词频统计了出来:
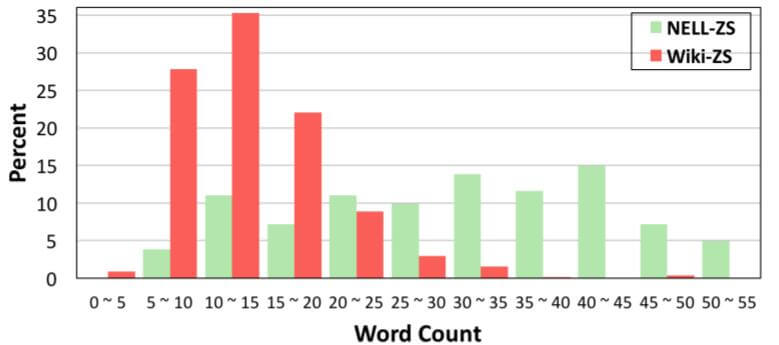
NELL - ZS的文本长度明显没有Wiki - ZS高.
在经过TF - IDF过滤后, 作者统计了TF - IDF > 0.3的词语个数:
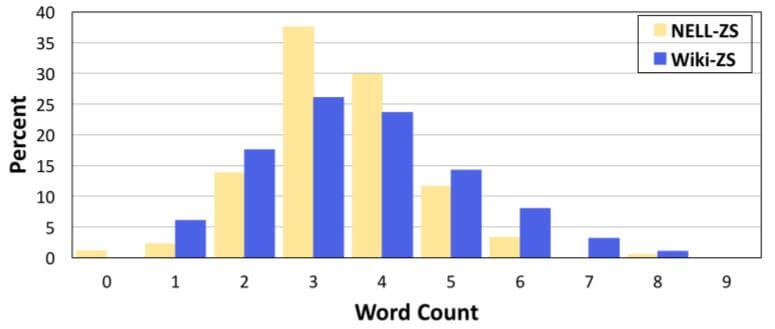
在使用了TF - IDF后, 大多数重要的词语都落在$[2, 5]$ 区间内, 说明TF - IDF能够比较有效的降噪.
Word Representations
作者其实尝试过现在非常流行的词向量表示BERT(Transformer Encoder):
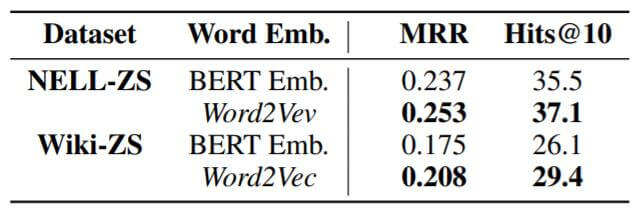
但实际上效果不理想, 作者认为其中与以下原因有关:
- BERT引入了更多的句子级噪声, 在这个任务上似乎句子中的信息是无效的.
- BERT产生的Word Embedding维度过高, 不利于GAN的训练.
我认为跟BERT的打开方式有一定的关联, Self - Attention本身就会根据句子中的其他内容来调整自身的表达, 跟TF - IDF的功能有一部分重复的地方.
Quality of Generated Data
作者为了评估生成器所生成的Relation Embedding的质量, 作者计算Feature Encoder生成的簇中心$x_r^c$ 和生成器生成的关系嵌入$\tilde x_r$ 之间的余弦相似度:
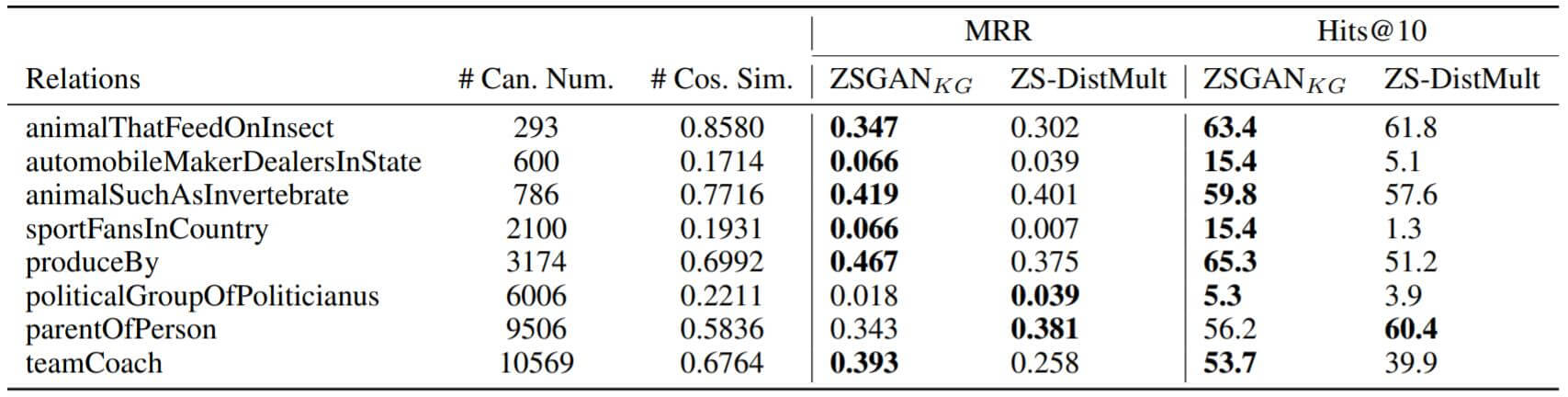
能看到, 生成器所生成的关系嵌入的余弦相似度基本与模型的MRR和Hits@10表现成正比.
Discussion
作者尝试过类似CNN, LSTM对Sentence建模的方法, 但都失败了. 作者认为这些方法都引入了更多的参数, 从而不利于GAN的学习, 会导致GAN的过拟合. 所以对句子建模只是使用简单的使用词袋模型, 结合TF - IDF. 此外, 现在作者方法中的实体均为闭集, 将来会考虑到实体在开集中的处理.
Summary
本文非常巧妙的想到用GAN结合KGE处理在未见过的关系上的问题. 作者通过使用Feature Encoder来构造真实的数据分布, 并通过一个简单的生成器来伪造数据, 当生成器能够很好的骗过判别器后, 直接使用生成器生成的Relation Embedding近似当做真实的Relation Embedding.
作者声称, 这是在KG领域的首个Zero - Shot关系学习方法.
抛开作者提出的方法本身不谈, 就作者在论文中提到关于GAN的内容来说, 有很大一部分是关于GAN的训练Trick. GAN虽然是一个非常好的idea. 但GAN的训练可能是一个很大的问题, 这点在实验结果中也多次提到, 在模型中引入的其他部分都有可能会对GAN的训练产生很大影响, 导致训练的不稳定.
Recommended
关于本文的:
关于文中涉及到的GAN:

