本文前置知识:
Learning Hierarchy-Aware Knowledge Graph Embeddings for Link Prediction
本文是论文Learning Hierarchy-Aware Knowledge Graph Embeddings for Link Prediction的阅读笔记和个人理解.
这篇讲解之所以把RotatE作为前置知识, 是因为HAKE与RotatE有很大关系, 并且通篇论文的论述也是与RotatE的对比. 本文有一部分参考于AAAI 2020 | 中科大:可建模语义分层的知识图谱补全方法.
Basic Idea
现有的KGE方法将注意力聚焦在对关系模式的建模上, 但没有对语义层级结构的建模, 而这种层级结构在现实世界的应用中是普遍存在的.
例如, mammal, dog, run, move 处于不同语义层级中, rose, peony, truck, lorry处于相同的语义层级中. 语义分层的现象在知识图谱所使用的三元组结构中是随处可见的. 并且可以进一步的将这种分层现象抽象成树形结构:
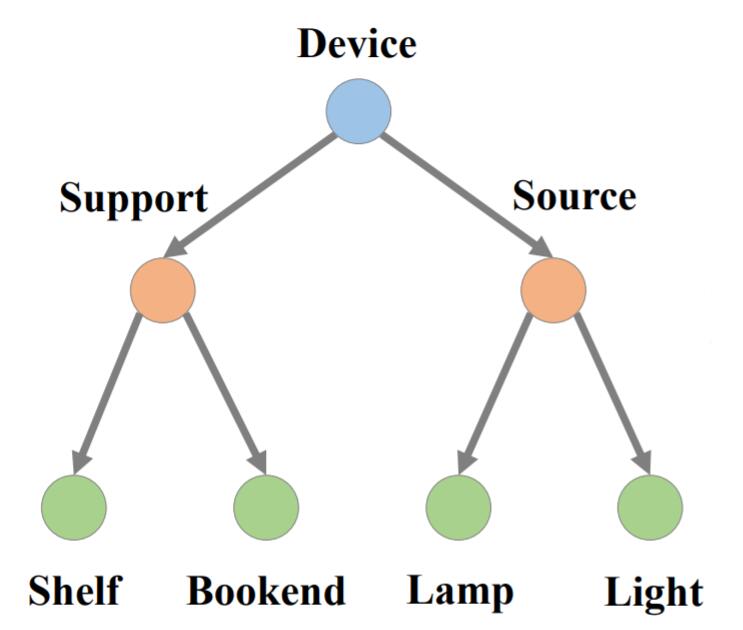
在这棵树中, 语义层级由上至下逐渐变得具体, 离根部越近的节点语义层级越高, 越抽象.
在本文中, 作者定义如下符号:
$$
[\mathbf{a} \circ \mathbf{b}]_{i}=[\mathbf{a}]_{i} \cdot[\mathbf{b}]_{i}
$$$[\mathbf{h}]_i$ 代表第$i$ 个实体的Embedding, $\lVert\cdot\rVert_1$, $\lVert \cdot \rVert_2$ 分别代表L1范数和L2范数.
HAKE
有了RotatE在复数空间建模的前车之鉴, HAKE希望在极坐标中直接对语义层次建模. 在极坐标中, 用极径(模长)$r$ 和角度$\rho$ 来表示在二维坐标系中的一个点, 模长和角度能完美的对语义层级建模:
- 模长部分对不同层级的实体建模.
- 角度部分对同一层级的实体建模.
想通过头实体$\mathbf{h}$ 在关系$\mathbf{r}$ 的作用下找到尾实体$\mathbf{t}$, 需要在极坐标中按照极坐标的运算规则来找到:
- 模长部分对应着固定角度下的放缩.
- 角度部分对应着固定模长时的旋转.
所以, 能把之前抽象出的树形结构直接用极坐标来表达:
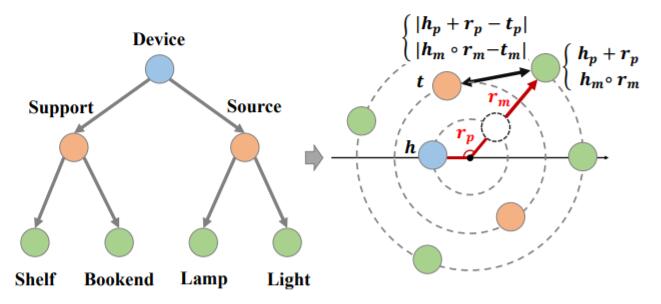
Hierarchy - Aware Knowledge Graph Embedding
Modulus Part
模长部分的关系被定义为对头实体模长的放缩:
$$
\mathbf{h}_{m} \circ \mathbf{r}_{m}=\mathbf{t}_{m}, \text { where } \mathbf{h}_{m}, \mathbf{t}_{m} \in \mathbb{R}^{k}, \text { and } \mathbf{r}_{m} \in \mathbb{R}_{+}^{k}
$$
模长所对应的距离函数为:
$$
d_{r, m}\left(\mathbf{h}_{m}, \mathbf{t}_{m}\right)=\lVert\mathbf{h}_{m} \circ \mathbf{r}_{m}-\mathbf{t}_{m}\rVert_{2}
$$
作者规定实体嵌入可以为负, 但约束Relation Embedding必须为正, 因为符号有助于尾实体的预测. 例如, 三元组$(h, r, t_1)$ 为正例, $(h, r, t_2)$ 为负例, 目标为最小化$d_r(\mathbf{h}_m, \mathbf{t}_{1, m})$, 最大化$d_r(\mathbf{h}_m, \mathbf{t}_{2, m})$.
- 对于正样本, $[\mathbf{h}]_i, [\mathbf{t}_1]_i$ 倾向于使用同一个符号, 因为$[\mathbf{r}_m]_i>0$.
- 对于负例, $[\mathbf{h}_m]_i, [\mathbf{t}_{2,m}]_i$ 可能是随机的符号.
这样, $d_r(\mathbf{h}_m, \mathbf{t}_{2, m})$ 会倾向于比$d_r(\mathbf{h}_m, \mathbf{t}_{1, m})$ 更大, 更有利于优化.
Phrase Part
相位部分的关系被定义为角度的旋转:
$$
\mathbf{h}_p+\mathbf{r}_p \approx\mathbf{t}_p
$$
通过求余的方式来解决相位的周期问题:
$$
\left(\mathbf{h}_{p}+\mathbf{r}_{p}\right) \bmod 2 \pi=\mathbf{t}_{p}, \text { where } \mathbf{h}_{p}, \mathbf{r}_{p}, \mathbf{t}_{p} \in[0,2 \pi)^{k}
$$
由于相位具有周期性, 所以相位所使用的距离度量函数应该与模长部分不同. 不能以简单的相位之差$\mathbf{h}_p + \mathbf{r}_p - \mathbf{t}_p$ 来度量两实体之间在相位部分的距离.
作者在这里使用了$\sin$ 来描述三元组中两实体的距离:
$$
d_{r, p}\left(\mathbf{h}_{p}, \mathbf{t}_{p}\right)=\lVert\sin \left(\left(\mathbf{h}_{p}+\mathbf{r}_{p}-\mathbf{t}_{p}\right) / 2\right)\rVert_{1}
$$
因为$\sin$ 是有负值的, 所以这里用L1范数(即绝对值)来约束$\sin$ 的结果.
该距离度量能很好的描述三者之间的相位距离关系.
因为对相位除了2, 所以周期变为$\pi$, 所以每当头实体的相位, 和关系相位, 与尾实体的相位的差$\mathbf{h}_p + \mathbf{r}_p - \mathbf{t}_p = k\pi, k\in(2k+1)$时, $(\mathbf{h}_p + \mathbf{r}_p - \mathbf{t}_p)/2 = \frac{\pi}{2}k, k\in (2k+1)$, 可以取到$\sin$ 函数的最大值1, 即此时距离最大.
Map into Polar Coordinate System
综合前两个小节, HAKE被整合进了极坐标系统中, 实体能在极坐标下唯一的被二维坐标标识.
$$
\left\{\begin{array}{l}
\mathbf{h}_{m} \circ \mathbf{r}_{m}=\mathbf{t}_{m}, \text { where } \mathbf{h}_{m}, \mathbf{t}_{m} \in \mathbb{R}^{k}, \mathbf{r}_{m} \in \mathbb{R}_{+}^{k} \\
\left(\mathbf{h}_{p}+\mathbf{r}_{p}\right) \bmod 2 \pi=\mathbf{t}_{p}, \text { where } \mathbf{h}_{p}, \mathbf{t}_{p}, \mathbf{r}_{p} \in[0,2 \pi)^{k}
\end{array}\right.
$$
距离函数是模长部分的距离函数和相位部分的组合:
$$
d_{r}(\mathbf{h}, \mathbf{t})=d_{r, m}\left(\mathbf{h}_{m}, \mathbf{t}_{m}\right)+\lambda d_{r, p}\left(\mathbf{h}_{p}, \mathbf{t}_{p}\right)
$$
其中$\lambda$ 为可学习的参数.
HAKE的打分函数如下:
$$
f_{r}(\mathbf{h}, \mathbf{t})=-d_{r}(\mathbf{h}, \mathbf{t})=-d_{r, m}(\mathbf{h}, \mathbf{t})-\lambda d_{r, p}(\mathbf{h}, \mathbf{t})
$$
因为距离越大, 打分应该越小, 所以这里在距离前面加上一个负号.
下图是HAKE与常见KGE模型的打分函数对比:

在跑实验时, 作者还发现了一种混合距离度量, 比原度量更加有效:
$$
d_{r, m}^{\prime}(\mathbf{h}, \mathbf{t})=\lVert\mathbf{h}_{m} \circ \mathbf{r}_{m}+\left(\mathbf{h}_{m}+\mathbf{t}_{m}\right) \circ \mathbf{r}_{m}^{\prime}-\mathbf{t}_{m}\rVert_{2}
$$
下面这个式子与上式是等价的:
$$
d_{r, m}^{\prime}(\mathbf{h}, \mathbf{t})=\lVert\mathbf{h}_{m} \circ\left(\left(\mathbf{r}_{m}+\mathbf{r}_{m}^{\prime}\right) /\left(1-\mathbf{r}_{m}^{\prime}\right)\right)-\mathbf{t}_{m}\rVert_{2}
$$
作者在后续实验发现这种方式有很大提升.
这个混合度量还有一些疑问, 以后研究.
Loss Function
HAKE与RotatE一样, 使用最大化间隔的损失函数来优化:
$$
L=-\log \sigma\left(\gamma-d_{r}(\mathbf{h}, \mathbf{t})\right)
-\sum_{i=1}^{n} p\left(h_{i}^{\prime}, r, t_{i}^{\prime}\right) \log \sigma\left(d_{r}\left(\mathbf{h}_{i}^{\prime}, \mathbf{t}_{i}^{\prime}\right)-\gamma\right)
$$
其中$\gamma$ 为间隔, $\sigma$ 为Sigmoid函数, $(h_i^\prime, r, t_i^\prime)$ 为负三元组.
HAKE也使用了RotatE中提到的自对抗负采样, 我在RotatE中已经有过讲解:
$$
p\left(h_{j}^{\prime}, r, t_{j}^{\prime} \mid\left\{\left(h_{i}, r_{i}, t_{i}\right)\right\}\right)=\frac{\exp \alpha f_{r}\left(\mathbf{h}_{j}^{\prime}, \mathbf{t}_{j}^{\prime}\right)}{\sum_{i} \exp \alpha f_{r}\left(\mathbf{h}_{i}^{\prime}, \mathbf{t}_{i}^{\prime}\right)}
$$
其中$\alpha$ 为Temperature.
除了带来性能上的提升外, HAKE在后续与RotatE对比时也显得更加公平.
Experiments
详细的参数设置请参照原论文.
Main Results
作者分别在WN18RR, FB15k - 237, YAGO3 - 10上做了实验, 它们的统计信息如下:
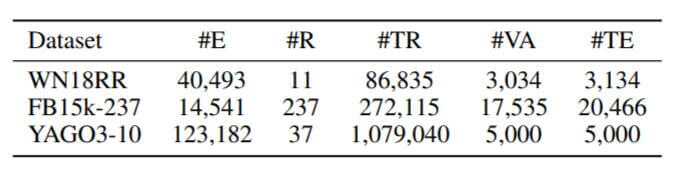
实验结果如下:
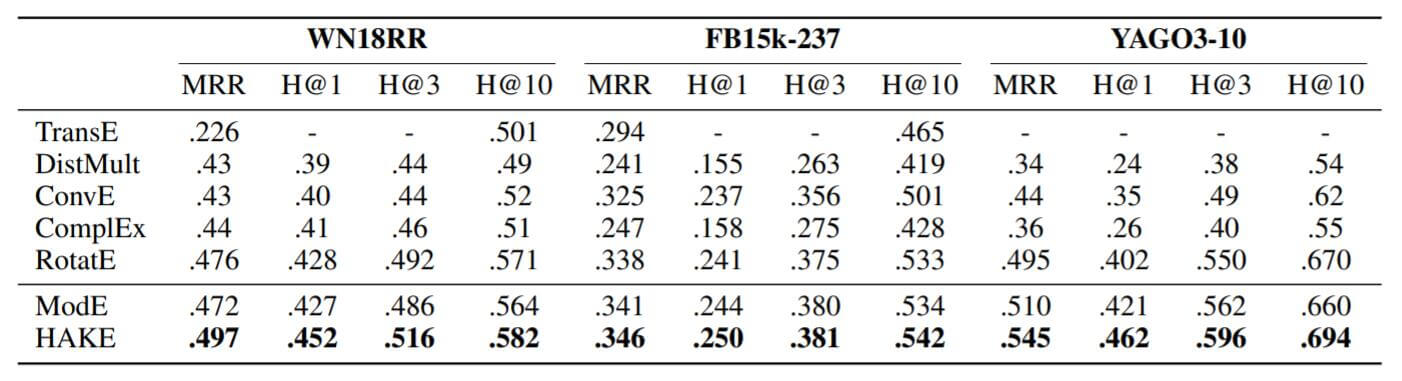
HAKE将相较于RotatE有一些提升, ModE和RotatE差不多.
Relation Embeddings Analysis
Modulus Part
作者把关系中所对应的实体模长分布直方图画了出来:
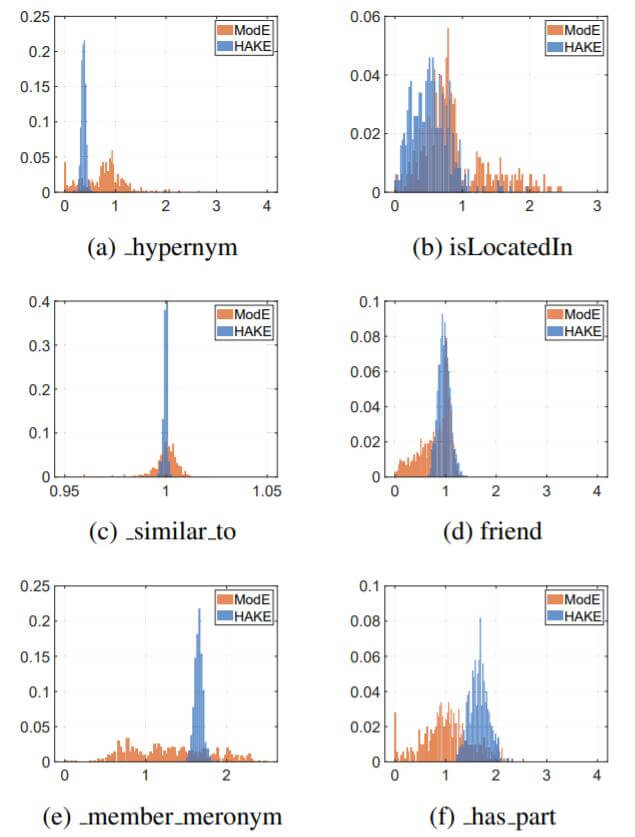
对于以关系$\mathbf{r}_m$作者有如下期望:
- 头实体相比于尾实体的语义层次更高时, 关系的模长$\mathbf{r}_{m}=\mathbf{t}_{m} / \mathbf{h}_{m}>1$.
- 头实体相比于尾实体的语义层次更低时, 关系的模长$\mathbf{r}_{m}=\mathbf{t}_{m} / \mathbf{h}_{m}<1$.
- 头实体与尾实体位于相同的语义层次时, 关系的模长$\mathbf{r}_{m}=\mathbf{t}_{m} / \mathbf{h}_{m} \approx 1$.
在作者展示出的六种关系中, 作者猜想得到了佐证.
Phrase Part
因为在上幅图中, _similar_to和friend没能利用模长做出区分, 作者将它们的相位分布做了出来:
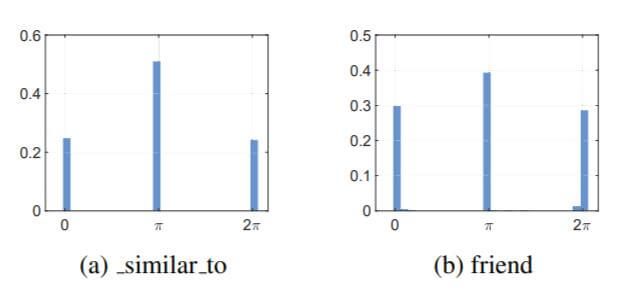
大多数的相位区分都集中在$\pi$ 的整数倍, 当相位差为$\pi$ 时, 实体可以被区分开.
Entity Embedding Analysis
将RotatE的实部, 虚部, HAKE的模长部分, 相位部分视为是二维坐标系中的坐标, 将它们的每个维度放到2D平面上可视化:
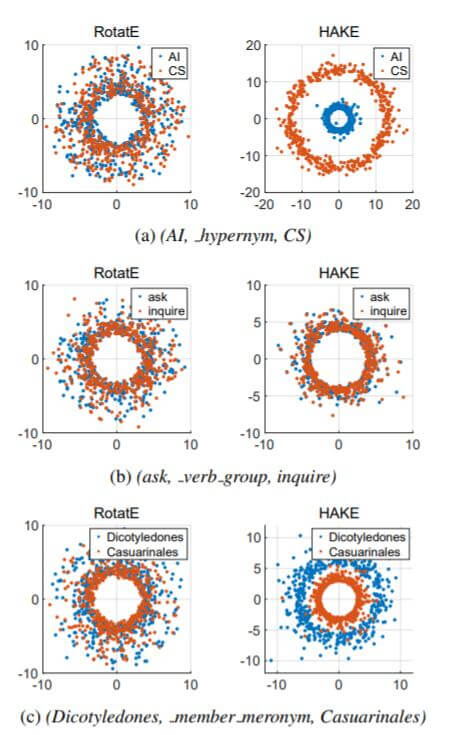
在RotatE中, 不同语义层级关系的实体是不能被区分开的, HAKE能保证不同语义层级的实体之间有一定的间隔, 相同语义层级之间的实体大致相同.
相同语义层级之间的实体可能被多元关系所包含, 它们从图(b)上来看是不好区分的, 暴露了HAKE不擅长处理多元关系的特性.
Ablation Studies
作者在三个数据集上做了相应的消融实验, 结果如下:
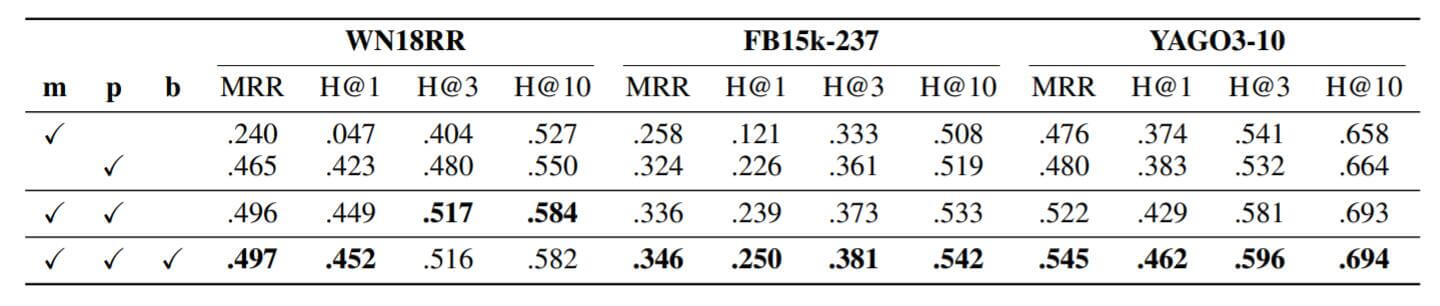
$\mathbf{b}$ 代表作者所称的混合距离度量.
如果只使用模长的部分, 性能是非常差的. 但如果只使用相位部分, HAKE将退化为pRotatE. 把二者混合性能可以得到进一步提升. 如果再采用混合距离度量性能还会有点提升.
Comparsion with Other Related Work
在FB15k上与四种TKRL的模型对比:

Summary
HAKE与RotatE相似, RotatE利用了复数空间的旋转建模关系, HAKE利用极坐标中的角度和模长建模语义层级结构.
作者着重与RotatE做了对比, 它确实比RotatE能针对语义层级关系做处理.
HAKE也十分的简洁, 但和RotatE一样, 理论上它还是只能做一对一的建模, 不善于处理多对一, 一对多, 多对多的多元关系.

