发布日期: 2021-04-18

更新日期: 2022-03-27

文章字数: 1.7k

阅读时长: 6 分

GAKE: Graph Aware Knowledge Embedding

本文是论文GAKE: Graph Aware Knowledge Embedding的阅读笔记和个人理解.

Basic Idea

在现有的KGE方法中, 都是基于三元组的, 但三元组之间是相互孤立的, 并没有利用上图信息.

作者尝试提出一种融入图结构信息的KGE方法.

GAKE

KG中的知识以图的结构按如下方式存在着:

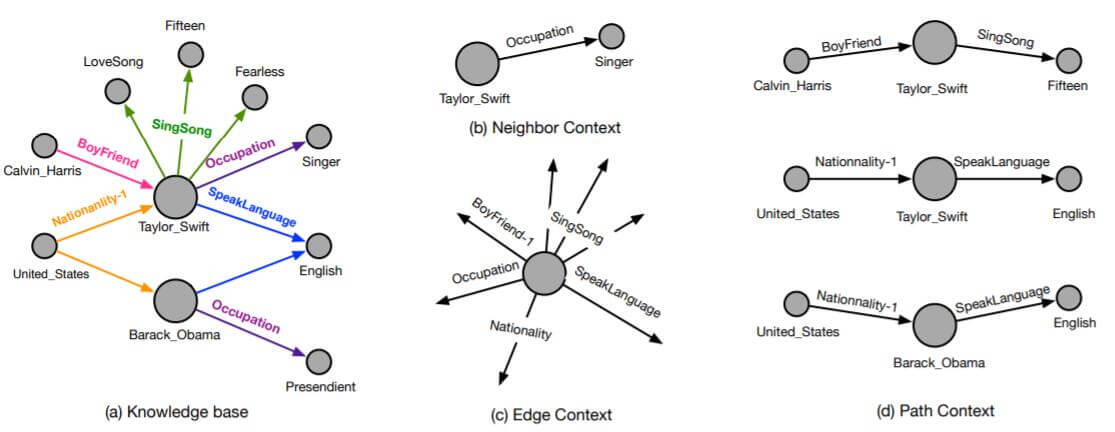
作者将图中的结构信息划分为三类:

邻居上下文(Neighbor Context)
边上下文(Edge Context)
路径上下文(Path Context)

如果能够处理图信息, 那么与其他KGE方法相比, 能够对Triple, Path, Edge同时建模:

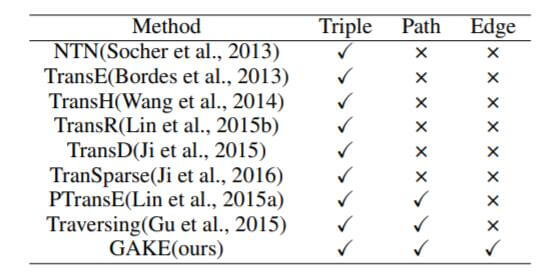
能够看到, 之前的方法一般都以三元组的方式对待KG, 即使融入路径信息, 也从未考虑图中的边信息.

Definitions

有向图可以被表示为$G=(V, E)$, $V, E$ 均为$G$ 中的Subject, 在GAKE中, 知识图谱$G=(V, E)$ 中的每一种顶点(实体)和每一种边(关系), 都是GAKE要学习的Embedding.

作者更一般的将$V, E$ 统称Subject $S$, 其中$s=(t, k)$. 当$t=0$ 时代表$s$ 为顶点, $t=1$ 时代表$s$ 为边. $k$ 为$s$ 在Subject Set $S$ 中的索引.

在给出Subject的定义后, 也能给出$s$ 上下文的定义. 对于给定的$s_i$, 其图上下文$c(s_i)$ 为与$s_i$ 相关的Subject Set $\left\{s_w \mid s_w \in S, s_w \text{ relevant to }s_i \right\}$. 因为Subject是很抽象的, 所以对于不同类型的Subject会有不同的Context定义.

作者还定义了如下符号: $C(s)$ 代表$s$ 的图上下文, $\phi(s)$ 代表取$s$ 的Embedding, $\pi(C(s))$ 代表获取$s$ 在上下文情况下的表示, $\theta$ 为模型参数.

Framework

GAKE是一种利用图结构信息的KGE范式, 其目标为预测图中缺失的Subject $s_i$, 那么缺失Subject $s_i$ 的概率应该在其上下文已知的情况下得到最大化:
$$
P\left(s_{i} \mid c\left(s_{i}\right)\right)=\frac{\exp \left(\phi\left(s_{i}\right)^{\top} \pi\left(c\left(s_{i}\right)\right)\right)}{\sum_{j=1}^{|S|} \exp \left(\phi\left(s_{j}\right)^{\top} \pi\left(c\left(s_{i}\right)\right)\right)}
$$
其中, $\pi(\cdot)$ 为聚合函数, 在这里先用简单的平均求和来计算各种上下文因素对$s_i$ 的影响:
$$
\pi\left(c\left(s_{i}\right)\right)=\frac{1}{\left|c\left(s_{i}\right)\right|} \sum_{s_{j} \in c\left(s_{i}\right)} \phi\left(s_{j}\right)
$$

Neighbor Context

给定一个Subject $s_i$, 以$s_i$ 是实体为例, 它的上下文是它的每个一阶邻居和它们之间的关系. 所以$s_i$ 为实体时, 邻居上下文和$s_i$ 的所有相关三元组无异.

然后采用极大似然优化$s_i$ 的概率:
$$
O_{N}=\sum_{s_{i} \in S} \sum_{c_{N}\left(s_{i}\right) \in C_{N}\left(s_{i}\right)} \log p\left(s_{i} \mid c_{N}\left(s_{i}\right)\right)
$$
$C_N(s_i)$ 是$s_i$ 的Neighbor Context.

作者没有说明Relation的邻居上下文是什么样的, 代码里也只是构造的实体邻居, 应该是本来就没有定义.

Path Context

KG中的路径直接或间接的反映了实体之间的关系. 因此, 作者定义Path Context $c_P(s_i)$ 为Random Walk生成的一系列顶点和边的集合.

与Neighbor Context类似, 也是用极大似然去优化:
$$
O_{P}=\sum_{s_{i} \in S} \sum_{c_{P}\left(s_{i}\right) \in C_{P}\left(s_{i}\right)} \log p\left(s_{i} \mid c_{P}\left(s_{i}\right)\right)
$$

Edge Context

对于一个实体, 所有与之直接相连的边都可能反映实体本身的情况. 因此, 当Subject为顶点时, Edge Context $c_E(s_i)$ 为$s_i$ 的边集.

同样, 还是用极大似然去优化:
$$
O_{E}=\sum_{s_{i} \in S} \log p\left(s_{i} \mid c_{E}\left(s_{i}\right)\right)
$$

Context extension

在作者提出的范式下, 如果有其他形式的Graph Context也可以继续扩展, 因为$c(s_i)$ 的含义可以随着对Context的定义变化而改变, 保证了一定的灵活性.

Attention Mechanism

在现实生活中, 每个Subject Context对Subject的本身的影响可能是不同的, 如果使用之前说的平均求和就略显不妥. 作者使用Attention机制对$s_i$ 的上下文元素加权求和, 使得模型更加灵活, 也更契合场景.

$a(s)$ 代表$s$ 所占的注意力权重, Attention计算方式如下:
$$
a\left(s_{i}\right)=\frac{\exp \left(\theta_{i}\right)}{\sum_{s_{j} \in C\left(s_{i}\right)} \exp \left(\theta_{j}\right)}
$$
$\theta$ 为要优化的参数.

在Attention机制下, $s_i$ 会受到其上下文元素的加权影响:
$$
\pi\left(c\left(s_{i}\right)\right)=\sum_{s_{j} \in c\left(s_{i}\right)} a\left(s_{j}\right) \phi\left(s_{j}\right)
$$
当模型预测English时, 对上下文所分配的各类权重是不同的:

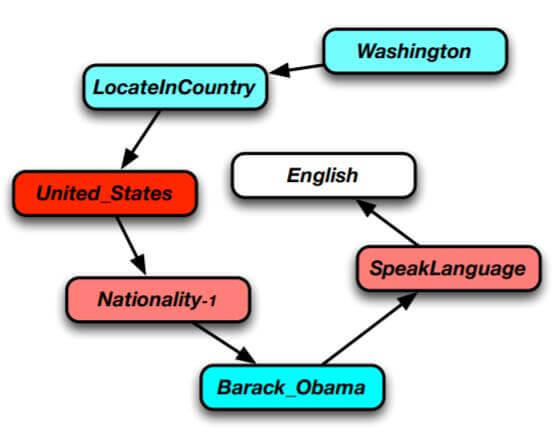
深暖色代表分配的注意力权重多, 冷色代表分配的注意力权重少. United_States, Nationality-1, SpeakLanguage 分配的权重就比较大, 因为它们能直接或间接的推导出English.

Model Learning

在训练模型时, 作者将上述三种目标函数整合到一起:
$$
O=\lambda_{N} O_{N}+\lambda_{P} O_{P}+\lambda_{E} O_{E}
$$
$\lambda_N, \lambda_P, \lambda_E$ 分别是Neighbor Context, Path Context, Edge Context所对应的占比, 总和为1. 在后续实验中, 作者定义$\lambda_N=0.8, \lambda_P=0.1, \lambda_E=0.1$, 强调了Neighbor Context的作用.

Experiments

详细的参数设置请参照原论文.

Triple Classification

作者在FB15K上做了三元组分类实验, 并与其他方法对比:

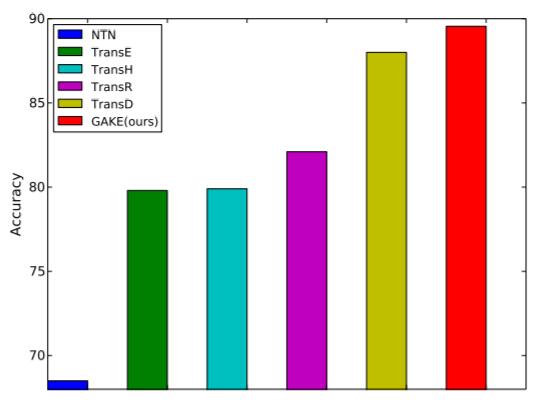
GAKE要优于其他方法, 达到近乎90%左右的准确率.

为了更好展示Attention在GAKE中起到的作用, 作者对预测Terminate2:JudgementDay时的其他路径上下文所占的注意力权重展示出来:

Action和Sequel所占的比重非常大, 因为终结者2是一部动作电影, 还是续集. Genre占的比重比较少, 因为每部电影都有所对应的体裁, 最起码在这条路径中, 体裁没那么重要.

Link Prediction

作者还做了链接预测任务, 在FB15K上的实验结果如下:

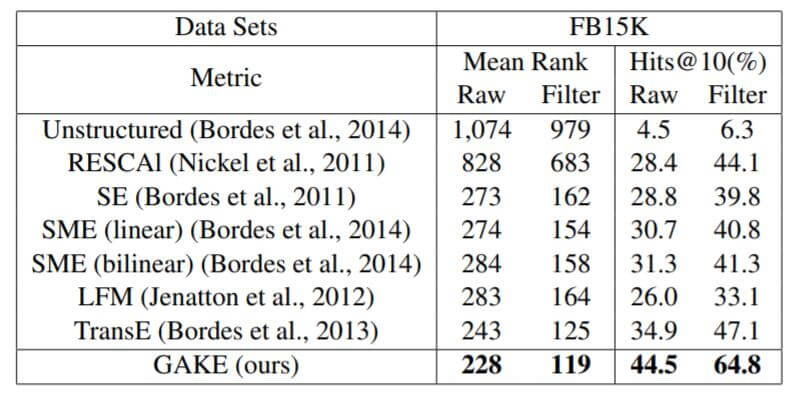
相较于其他早期的KGE方法, GAKE的性能有明显提升.

Summary

本文发布于COLING2016, 算是一篇相对比较早的文章了. 作者提出了在KGE中同时使用Neighbor Context, Path Context, Edge Context三种上下文来融入图结构信息, 并用Attention去增强图结构对Subject的表示, 取得了比较好的效果.