Introduction: Vector Quantization
Vector Quantization
AutoEncoder(AE)由Encoder和Decoder组成, Encoder将图像压缩为一个低维的隐向量(Latent), 再由Decoder使用Latent将图像恢复出来. 在此基础上有向原始图像中加噪的Denoising AutoEncoder(DAE)和从将Latent规约为标准正态分布的生成式模型Variational AutoEncoder(VAE)两种. 我们在之前的博客中已经讲述过了:
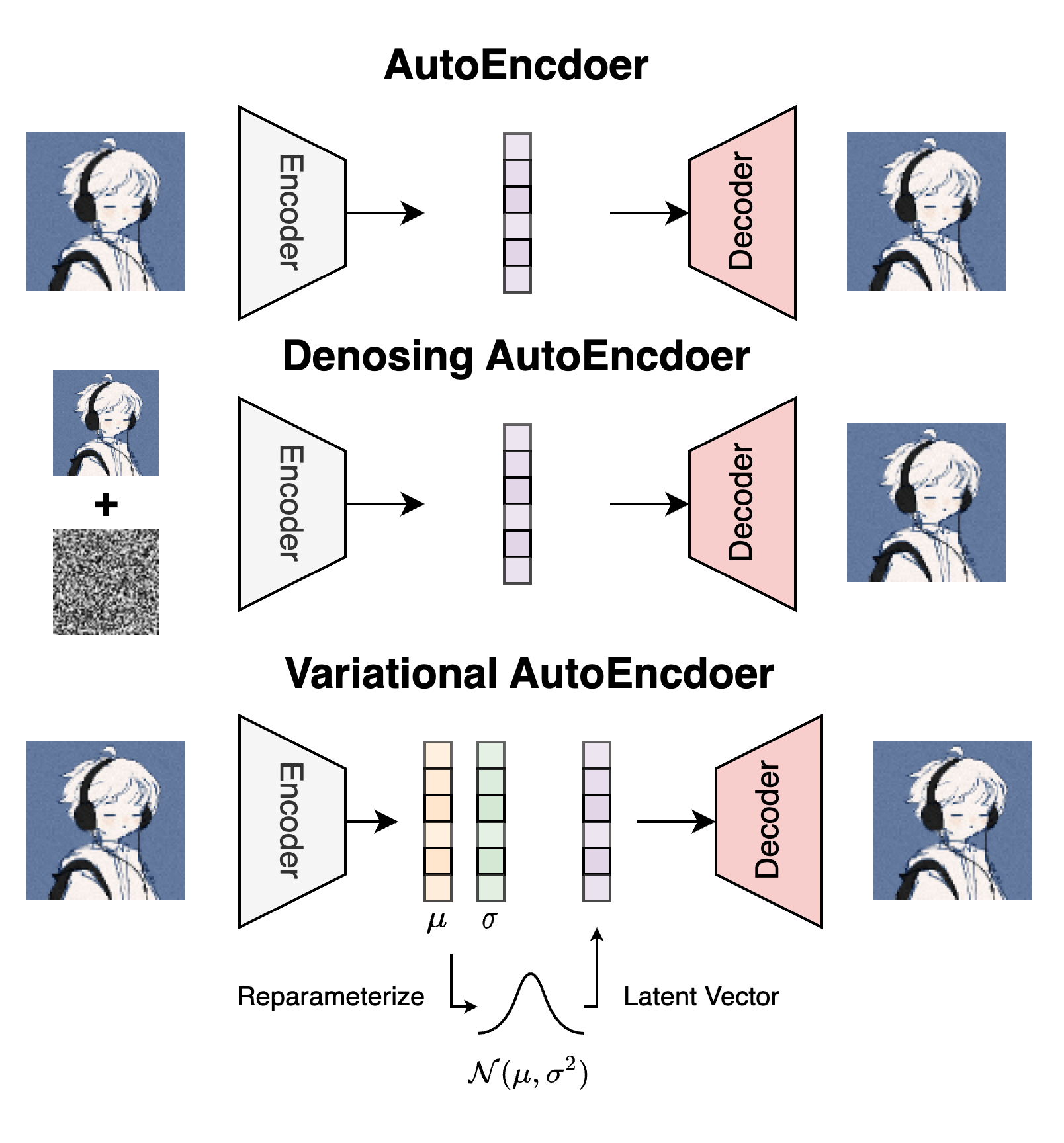
它们的Latent Vector都是连续的, 能不能将中间的Latent从连续变成一个离散的状态呢?
因为有时, 物体的特征可能是一种离散状态, 此时我们不希望样本在Latent Space连续的分布.
例如人是否在坐着, 只能是坐与不坐两种状态, 不能介于二者之间变成一个即坐又不坐的状态. 如果是连续的Latent Space设计, 模型可能会学习到从坐到不坐的连续变化过程, 但实际上它并不应该存在.
我们可以通过Vector Quantization(VQ)来实现这一想法:
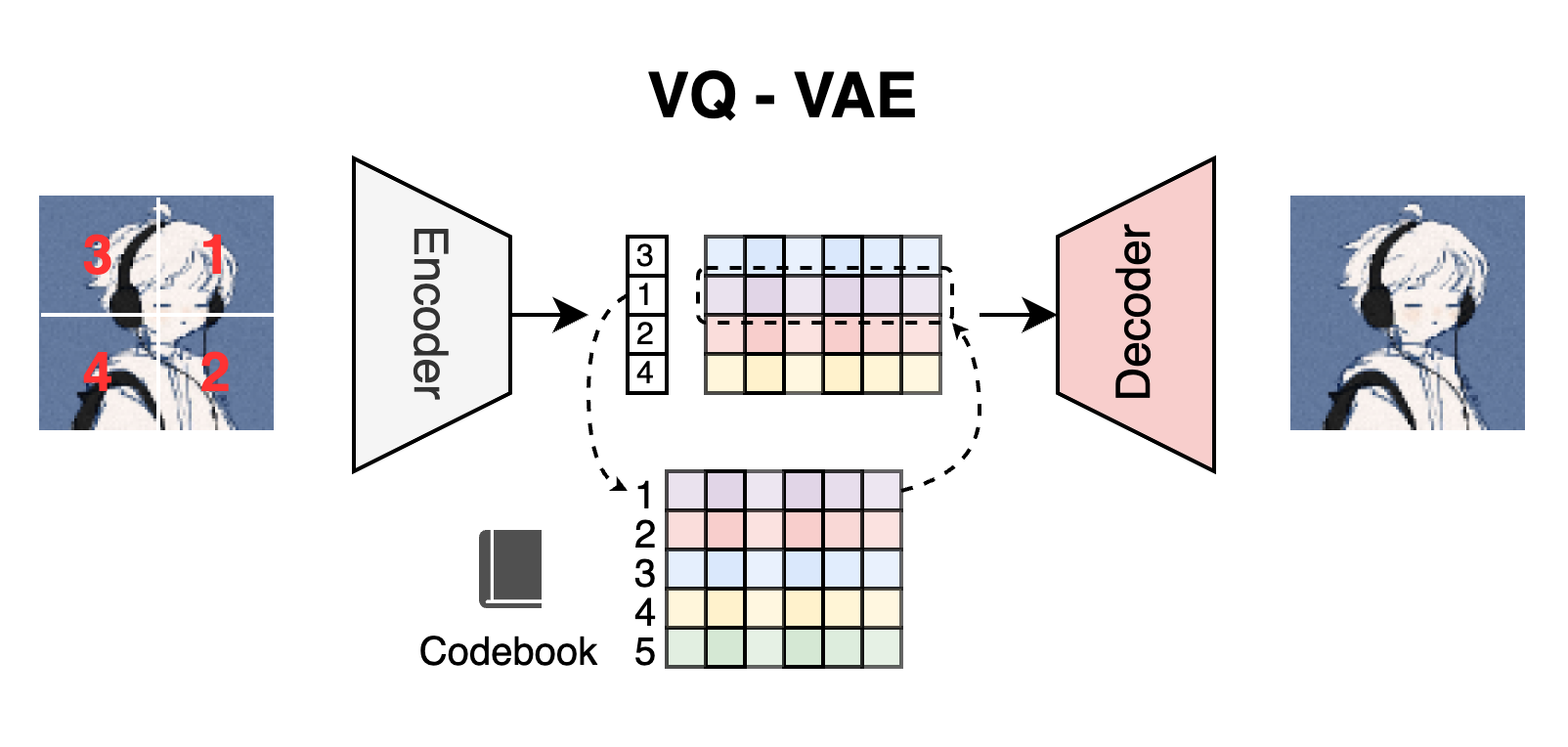
VQ - VAE
Discrete Latent Variables
VQ - VAE仍然遵循AE的框架, 它也有Encoder $z_e$, Decoder $z_q$. 对图像用Encoder抽得一个表示$z_e(x)$, 然后用Decoder对输入$z_q(x)$ 解码, 得到原图像$x$.
与一般AE不同的是, VQ - VAE额外有一个Codebook, 存放了$K$ 个$D$ 维的Embedding $e_i \in \mathbb{R}^D$, 称为Latent Embedding Space $e \in \mathbb{R}^{K \times D}$. 这个Codebook也可以看做是VQ - VAE的先验分布, 只不过它是离散的.
在Latent处, 后验类别分布$q(z|x)$ 也不再是连续空间, 而是离散空间, 这与做一个$K$ 分类任务类似. 其分布可以用One - Hot来表示:
$$
q(z=k \mid x)= \begin{cases}1 & \text { for } \mathrm{k}=\operatorname{argmin}_j\left\Vert z_e(x)-e_j\right\Vert_2 \\\ 0 & \text { otherwise }\end{cases}
$$
接下来, 将Encoder抽取到的图像表示$z_e(x)$ 直接替换为Codebook中离$z_q(x)$ 距离最近的$e_k$, 并作为Decoder的输入$z_q(x)$:
$$
z_q(x)=e_k, \quad \text {where} \quad k=\operatorname{argmin}_j\left\Vert z_e(x)-e_j\right\Vert_2
$$
由于其中有$\text{argmin}$, 所以这里存在梯度断裂, Decoder侧的梯度是没法通过链式法则传到Encoder做更新的.
注意, 这里Encoder抽取出的表示$z_e(x)$ 一般是一个用CNN获得的$m \times m \times D$ 的特征, 所以这张图像$x$ 对应的离散表示就是一个$m \times m$ 的二维矩阵. 如果$z_e(x) \in \mathbb{R}^D$, 在重构的时候就比较困难了, 这代表着Codebook里的某个Embedding对应了若干张训练集图片, 而不是图像中的某个部分.
Learning
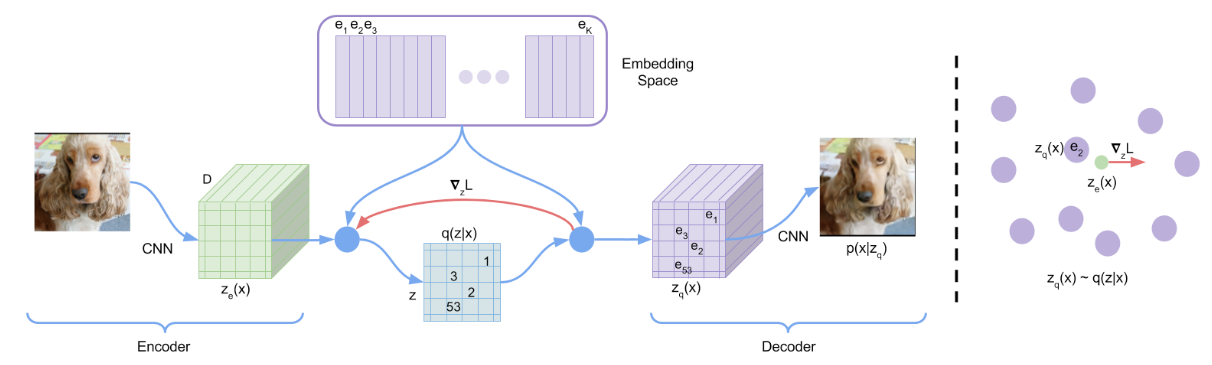
接上文, 因为Encoder的输出$z_e(x)$ 维度和Decoder输入$z_q(x)$ 维度是一致的, 作者使用Straight - Through Estimator(STE), 直接将Decoder input处$z_q(x)$ 的梯度Copy到Encoder output处$z_e(x)$即可, 这样就链接了Encoder和Decoder的梯度更新, 官方给出的代码如下:
decoder_input = z_e + (z_q - z_e).detach()虽然作者引入的STE解决了Encoder和Decoder的梯度更新, 但如果按照上述代码来走, Codebook里面的Embedding的梯度没法通过Decoder拿到了, 因为z_q 的梯度被detach掉了. 这样就需要通过额外约束来优化Codebook.
Codebook中的Embedding $e$ 肯定是希望离Encoder的输出$z_e(x)$ 越近越好, 这样才说明Codebook的对应Embedding $e_i$ 跟Encoder输出匹配的更好, 也更有利于Decoder做生成, 因为$z_q(x) = e_k$ 嘛.
最终, Training Loss共包含三个部分:
$$
L=\underbrace{\log p\left(x \mid z_q(x)\right)}_{\text{Reconstruction}}+\underbrace{\left\Vert \operatorname{sg}\left[z_e(x)\right]-e\right\Vert _2^2}_{\text{VQ}}+\beta\underbrace{\left\Vert z_e(x)-\operatorname{sg}[e]\right\Vert _2^2}_{\text{Commitment}}
$$
其中, $\text{sg}$ 为Stop Gradient Operator.
- 第一项为Reconstruction Loss, 就是由Decoder重建图像的Loss, 与AE损失相同. 并由STE链接Encoder和Decoder的梯度更新.
- 第二项为VQ Loss, 负责让Codebook中的Embedding $e$ 离Encoder output $z_e(x)$ 更近.
- 第三项为Commitment Loss, 这是与第二项对称的Loss, 前面多乘上了一个超参$\beta$ 用于调节比例, 负责让Encoder output$z_e(x)$ 也朝着$e$ 移动. 作者认为Codebook Embedding无量纲, 且Codebook和Encoder的参数更新速度不同添加的.
另外, $\beta$ 文中作者取0.25, 并且作者发现从0.1取到2.0模型表现变化都不大.
看到这里, 能够发现VQ - VAE实际上并不是一个VAE, 它和VAE没有任何关系, 只是一个用VQ实现的AE. 因为只靠VQ - VAE自己是不能直接生成若干张不同随机图像的, 因此它只能看做是一种压缩方式, 图像从原始输入大小$H \times W \times 3$变成了更小的二维矩阵$m \times m$. 如果想要做生成, 需要结合PixelCNN完成.
VQ - GAN
VQ - GAN实际是VQ-VAE的一种变体, 都是利用VQ, 但VQ - GAN用了Transformer做自回归生成. VQ - VAE的自回归生成采用的是PixelCNN, 这种级别的模型对于自回归生成来说还是比较脆弱的. 恰好, Transformer擅长自回归离散Token序列的生成, 所以Transformer理应成为Autoregressive Manner的首选.
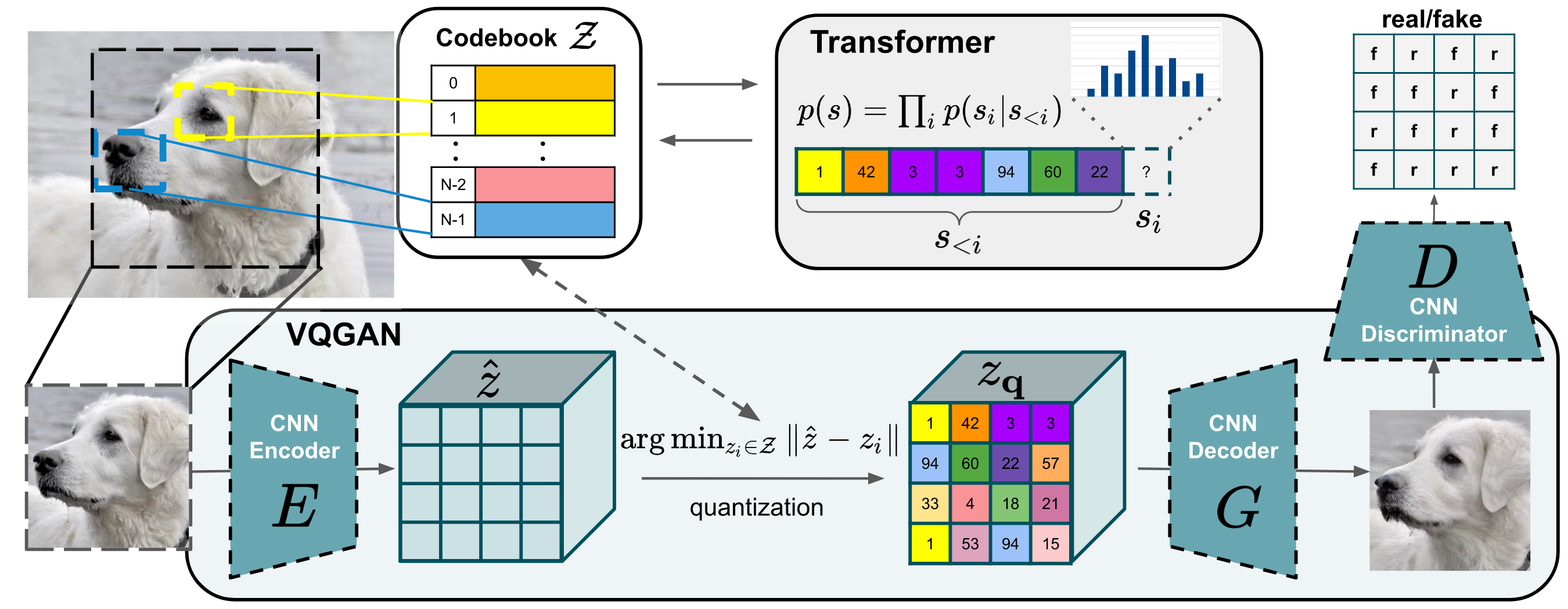
Learning an Effective Codebook of Image Constituents for Use in Transformers
与VQ - VAE类似的, VQ - GAN中生成用的主体有Encoder $E$, Decoder $G$(因为这里是GAN, 所以Decoder是生成器$G$), 和Codebook $\mathcal{Z} = \set{z_k}^{K}_{k=1} \subset \mathbb{R}^{n_z}$.
对于给定的图片$x \in \mathbb{R}^{H \times W \times 3}$, 首先用CNN的Encoder $E$ 抽取出图像$x$ 的编码表示$\hat{z} = E(x) \in \mathbb{R}^{h \times w \times n_z}$.
然后, VQ - GAN会用一个由$h \times w$ 个$n_z$ 维的Embedding组成的二维特征矩阵$z_\mathbf{q} \in \mathcal{R}^{h \times w \times n_z}$ 作为CNN Decoder $G$ 的输入.
这里的VQ的过程与VQ - VAE是一样的, 都是用最近邻替换每个Spatial Code$\hat{z}_{ij} \in \mathbb{R}^{n_z}$:
$$
z_{\mathbf{q}}=\mathbf{q}(\hat{z}):=\left(\underset{z_k \in \mathcal{Z}}{\arg \min }\left\Vert \hat{z}_{i j}-z_k\right\Vert \right) \in \mathbb{R}^{h \times w \times n_z}
$$
将$z_{\mathbf{q}}$ 作为Decoder $G$ 的输入, 重建图像$\hat{x}$:
$$
\hat{x}=G\left(z_{\mathbf{q}}\right)=G(\mathbf{q}(E(x)))
$$
与VQ - VAE同样的, 由于Decoder $G$ 和Encoder $E$ 中间的quantization存在$\text{argmin}$, 所以梯度不能从$G$ 传递到$E$, VQ - GAN也使用了STE, 与VQ - VAE形式一样的Loss $\mathcal{L}_{\text{VQ}}$如下:
$$
\mathcal{L}_{\mathrm{VQ}}(E, G, \mathcal{Z})=\Vert x-\hat{x}\Vert ^2 +\left\Vert \operatorname{sg}[E(x)]-z_{\mathbf{q}}\right\Vert _2^2+\beta\left\Vert \operatorname{sg}\left[z_{\mathbf{q}}\right]-E(x)\right\Vert _2^2
$$
虽然MSE可以从像素角度来描述图像之间的相似性, 但并不能从抽象的特征角度描述图像重构的好不好, 所以作者将L2 Loss $\Vert x-\hat{x}\Vert^2$ 替换为Perceptual Loss $\mathcal{L}_{\text{rec}}$:
$$
\mathcal{L}_{\mathrm{VQ}}(E, G, \mathcal{Z})=\mathcal{L}_{\text{rec}} +\left\Vert \operatorname{sg}[E(x)]-z_{\mathbf{q}}\right\Vert _2^2+\beta\left\Vert \operatorname{sg}\left[z_{\mathbf{q}}\right]-E(x)\right\Vert _2^2
$$
据说作者给的代码MSE和Perceptual Loss都用了.
Learning a Perceptually Rich Codebook
因为是GAN嘛, 训练GAN除了有Generator, 还需要有一个Discriminator. 作者用一个Patch - based Discriminator $D$ (其实就是PatchGAN)来评估Decoder $G$ 将每个Code生成为Patch的真假, 即对$h \times w$ 个Patch的真假都做判断:
$$
\mathcal{L}_{\mathrm{GAN}}(\{E, G, \mathcal{Z}\}, D)=[\log D(x)+\log (1-D(\hat{x}))]
$$
最终目标函数为找到最优模型参数$\mathcal{Q}^\ast = \set{E^\ast, G^\ast, \mathcal{Z}^\ast}$:
$$
\mathcal{Q}^\ast=\underset{E, G, \mathcal{Z}}{\arg \min } \max _D \mathbb{E}_{x \sim p(x)}{\left[\mathcal{L}_{\mathrm{VQ}}(E, G, \mathcal{Z})\right.} \left.+\lambda \mathcal{L}_{\mathrm{GAN}}(\{E, G, \mathcal{Z}\}, D)\right]
$$
对应的Loss就是前面说过的VQ Loss和GAN Loss两项之和.
GAN的Loss最外层是Minimize $E, G, \mathcal{Z}$, 最内层是Maximize $D$, 所以它的目标其实是在有一个具有真正判别能力的判别器$D$ 的情况下优化生成器$G$ 的参数.
其中, $\lambda$ 为自适应权重:
$$
\lambda=\frac{\nabla_{G_L}\left[\mathcal{L}_{\mathrm{rec}}\right]}{\nabla_{G_L}\left[\mathcal{L}_{\mathrm{GAN}}\right]+\delta}
$$
这个式子里的$\mathcal{L}_{\text{rec}}$ 是Perceptual Loss, $\delta$ 为1e-6, 防止分母零除.
作者在论文中没有给出$\lambda$ 的作用, 我们姑且可以认为$\lambda$ 是为了平衡$\mathcal{L}_{\text{rec}}$ 与$\mathcal{L}_{\mathrm{GAN}}$ 的影响而存在的, 保证两个Loss的作用差不多:
- 当$\mathcal{L}_{\text{rec}}$ 梯度大于$\mathcal{L}_{\mathrm{GAN}}$ 的梯度时, 说明模型生成的图像还不够好, 此时$\lambda > 1$, $\mathcal{L}_{\text{rec}}$ 影响比较大, 所以需要加强$\mathcal{L}_{\mathrm{GAN}}$ 的权重.
- 当$\mathcal{L}_{\text{rec}}$ 梯度小于$\mathcal{L}_{\mathrm{GAN}}$ 的梯度时, 说明模型生成的图像足够好, 此时$\lambda < 1$, $\mathcal{L}_{\text{rec}}$ 影响比较小, 所以需要削弱$\mathcal{L}_{\mathrm{GAN}}$ 的权重.
Learning the Composition of Images with Transformers
Latent Transformers
在通过VQ将输入图像$x$ 转化为$z_{\mathbf{q}}=\mathbf{q}(E(x))$ 后, 它等价于由Codebook $\mathcal{Z}$ 中Token下标组成的序列$s \in\{0, \ldots,|\mathcal{Z}|-1\}^{n \times w}$:
$$
s_{i j}=k \text { such that }\left(z_{\mathbf{q}}\right)_{i j}=z_k
$$
所以可以直接用Decoder - Only的Transformer对离散序列的自回归生成:
$$
\mathcal{L}_{\text {Transformer }}=\mathbb{E}_{x \sim p(x)}[-\log {\prod_i p\left(s_i \mid s_{<i}\right)}]
$$
Conditioned Synthesis
如果需要对图像合成附加上条件$c$, 只需要在Transformer生成序列前加上条件信息$c$, 接下来继续做自回归生成就好:
$$
p(s \mid c)=\prod_i p\left(s_i \mid s_{<i}, c\right)
$$
如果$c$ 只是简单的类别信息, 那么$c$ 就是一个简单的Embedding. 但如果是有约束条件$r$, 例如一个要生成图像的草图或框架, 那么$c$ 是一由一个新的Codebook和另一个专门编码条件的VQ - GAN得到的Conditional Sequence, 然后继续以Autoregressive Manner生成图像就可以了.
Generating High - Resolution Images
生成高清图像的话需要扩大每个图片对应的Code Embedding数量, 这样就会给Transformer做序列生成时候带来压力. 作者提出了一种基于Sliding window的方法, 每次生成Token的时候只关注一个局部的小窗来生成下一个Code:

只要数据集上满足近似平移不变, 或者附带空间信息, 就可以做到高清的图像生成了. 如果没有空间信息, 人为附加上一个空间信号, 依然可以用这种方法生成高清图像.
Recommended
VQ - VAE:
VQ - GAN:
VQ + Image Generation串讲:
Summary
在不同的Modality里, 都可以用VQ来做:
- CV: VQ最主要的作用是压缩图像的序列长度.
- NLP: Token Embedding的生成本身就遵循Autoregressive Manner, 本身就是离散的.
- Audio: 在语音领域中, 语音信号也需要做离散化处理, 用一个Quantizer把连续语音信号转化成离散的Token是一种常用的操作.
在以VL为主的MLLM时代, VQ因为使用Codebook能够统一离散形式的文本Token和图像生成而重新被人提起. 这种Multimodal Tokenization的方式或许能帮助MLLM更好的理解不同Modality之间的关系, 因此VQ或许能够在MLLM时代继续发挥它的光和热.
另外, Codebook中的每个Code很容易出现利用率不均, 这里抛砖引玉的给出一篇文章, 是对VQ - GAN的改进:

