发布日期: 2021-07-09

更新日期: 2022-06-24

文章字数: 2.9k

阅读时长: 11 分

Introduction: Variational Auto - Encoder

变分自动编码器(VAE, Variational Auto - Encoder)是一种基于自编码器结构的深度生成模型.

本文对VAE更深层次的数学原理没有探讨, 一般概率基础即可放心食用, 更深层次的数学原理在文末深入阅读处给出.

VAE与GAN有非常紧密的关系, GAN之后找个机会细说(先挖坑).

自编码器

本节图片全部出自Applied Deep Learning - Part 3: Autoencoders.

在介绍VAE之前, 必须要简要介绍一下自编码器(AE, Auto - Encoder).

自编码器是一种先把输入数据压缩为某种编码, 后仅通过该编码重构出原始输入的结构. 从描述来看, AE是一种无监督方法.

AE的结构非常明确, 需要有一个压缩编码的Encoder和就一个相应解码重构的Decoder:

Encoder能够将给定的输入$X$ 映射为编码$Z$, 即$Z=g(X)$, Decoder能将编码$Z$ 映射回与原输入相似的$\hat{X}$, 即$\hat{X}=f(Z)$. $Z$ 也被称为隐变量, 其维度必须是远远小于$X$ 的, 否则就达不到压缩编码的目的.

如果Decoder能仅依赖Encoder生成的编码$Z$ 尽可能好的还原输入数据, 那么就说明$Z$ 中真的存在某种能表征原始输入$X$ 的信息, 甚至$Z$ 的每一维都可能对应着某个输入数据变化的具体含义, 例如人脸的笑容, 褶皱, 皮肤颜色等属性.

对于压缩编码和解码重构的结构, 使用普通的神经网络, 只需要让神经元的个逐渐减少到编码的维度, 再由编码维度逐渐增大到原输入维度:

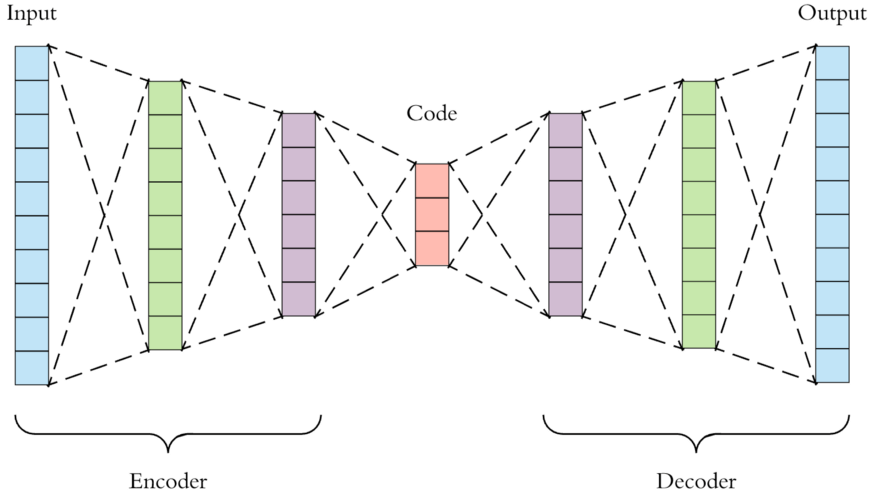
Encoder和Decoder的不一定是完全对称的, 甚至也不一定是同质的.

我们希望Auto Encoder所重构的输入$\hat{X}$ 和真正输入$X$ 的差距越小越好, 所以通常使用均方误差(MSE)来作为AE的损失函数, 即$\mathcal{L}_{MSE}=\Vert X - \hat{X} \Vert ^ 2$.

AE有一种常见的变形, 称为去噪自编码器(Denoising Auto - Encoder). 这种AE在原始输入数据的基础上添加了噪声, 然后再将其送给AE, 并要求Decoder还原出不带噪声的输入数据. 这就要求Encoder和Decoder具有更强大的能力:

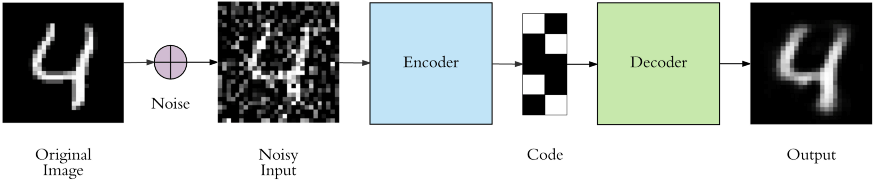
AE不是我们今天的重点, 就不再展开说了.

仔细想想, Auto Encoder虽然是可以分成Encoder和Decoder两个部分, 但实际上Encoder和Decoder是没法作为两个组件单独使用的, 它们必须配套使用.

例如我们想用单独使用Decoder做生成, 我们只能把随机生成的向量输入到Decoder中, 强行让Decoder解码出一个极少概率有用的内容, 效果一定不会很好. 因为在训练时, Decoder获得的编码全部是来自于Encoder的, 而我们直接随机采样得到的向量与Encoder压根没有关联, 让Decoder解码出有效的结果是不可能的.

变分自编码器

本节图片出自Variational autoencoders., 内容讲解参考苏神的博客.

变分自编码器(VAE, Variational Auto - Encoder)从概率的角度描述隐空间与输入样本.

隐变量 - 概率分布式

理想形态下的生成模型可以被描述为$X = g(Z)$. 由于没法直接知道$p(X)$, 我们得引入隐变量$Z$ 来求:
$$
p(X) = \sum_Z p(X\mid Z) p(Z)
$$

如果我们能把输入样本$X$ 编码得到的$Z$ 控制在我们已知的某个分布中, 那么我们就可以从隐变量的分布中采样, 解码得到生成内容$\hat{X}$, 也算不错.

在这样的想法下, 将样本的隐变量建模为概率分布, 而非像AE一样把隐变量看做是离散的值:

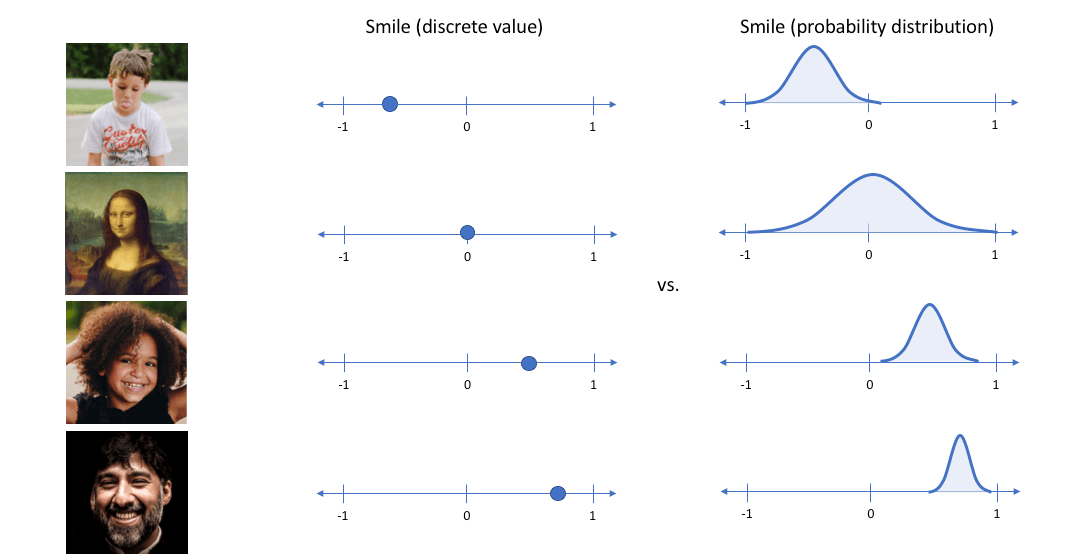
AE将样本编码为离散的点, 而VAE将样本编码为概率分布, 直接点就是给隐变量添加噪声.

那么在Decoder解码时, 从隐变量中随机采样, 得到采样后的向量作为Decoder的输入:

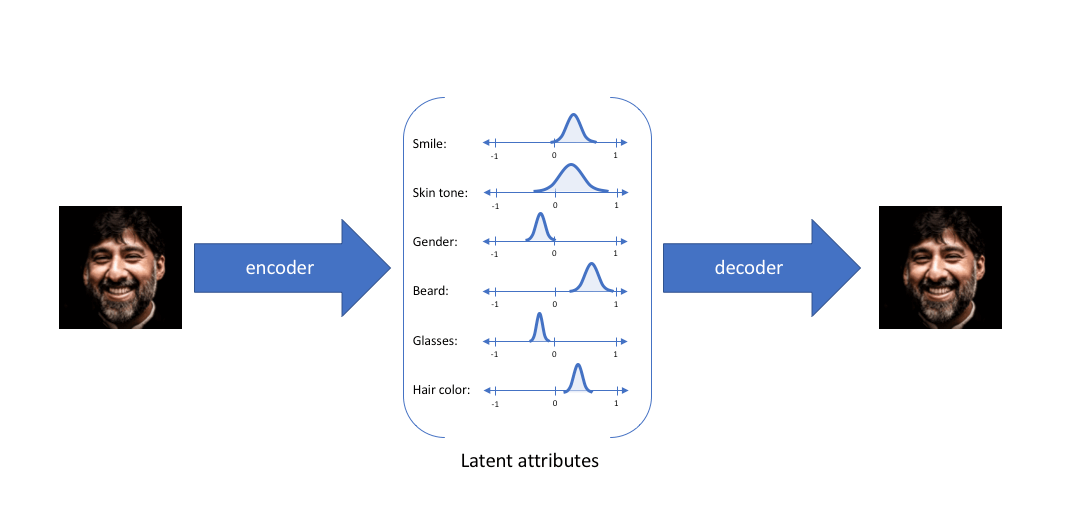
沿着这个思路, 如果假设$p(Z) \sim \mathcal{N}(\mu, \sigma^2)$, 可以从其中采样得到$Z_1, Z_2 , \dots, Z_n$, 然后由生成模型得到$\hat{X}_1 = g(Z_1),\hat{X}_2 = g(Z_2),\dots,\hat{X}_n = g(Z_n)$, 但我们根本没法度量生成的结果$\{\hat{X}_1,\hat{X}_2,\dots,\hat{X}_n\} $ 和样本数据$\{X_1,X_2,\dots,X_n\}$ 之间的差异, 因为我们压根不知道$Z_k, X_k, \hat{X}_k$ 之间的对应关系.

没有$X, \hat{X}$ 分布的表达式, 我们就没有办法通过对齐二者分布的方法来优化模型.

所以, 我们应该在给定真实样本$X_k$ 的情况下, 假设存在分布$p(Z \mid X_k) \sim \mathcal{N}(\mu, \sigma^2)$. Decoder就可以把$p(Z \mid X_k)$ 中采样得到的$Z_k$ 还原为$X_k$, 这样保证$Z_k, X_k, \hat{X}_k$ 之间可以对应.

尽管分布内采样到的隐变量的值不完全相同, 但都应该重建回相同的输出, 这也就是把样本编码为概率分布的真正含义:

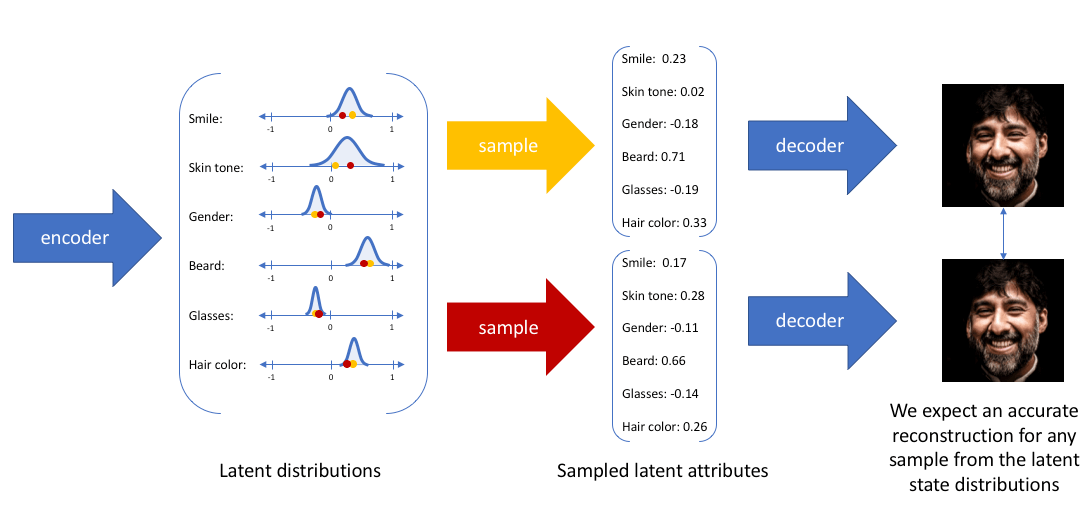
每一个样本都对应着一个自己专属的正态分布, 样本之间必定存在重合, 当采样到两个样本叠加的区域时, 解码的内容会变得介于二者之间. 按照AE中的假设, 隐变量的每维都可能有具体的含义. 若是如此, 在概率分布视角下的隐变量就可以等距采样, 通过观察控制生成的内容. 例如:

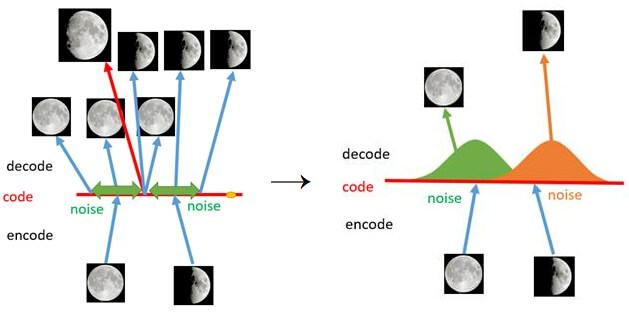
从满月到半月等距采样, 应该能观察到由满月逐渐变到半月的所有月相.

本图出自李宏毅老师课程配套Slide.

那每个分布的均值和方差要怎么求出来呢? 没什么好方法, 用神经网络来直接拟合样本对应的正态分布的均值$\mu$ 和方差$\sigma^2$ 吧:

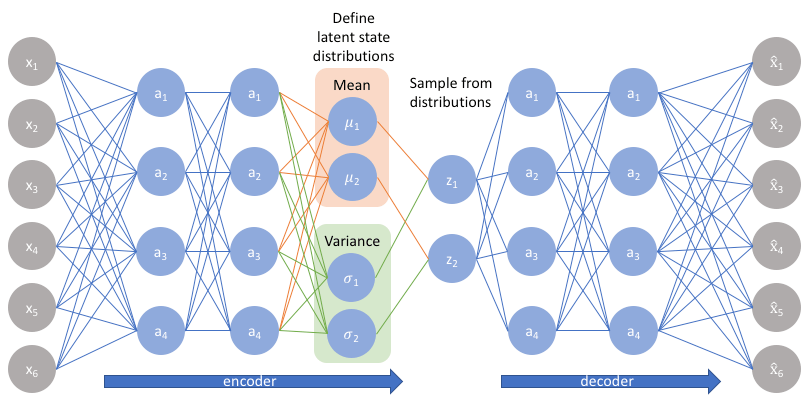
但我们实际上拟合的是$\log \sigma^2$, 因为$\sigma^2$ 非负, 想要让变为负数需要加激活函数处理, 而$\log \sigma^2$ 可以直接在不加激活函数的情况下变为负值.

KL散度 - 防止神经网络偷懒

神经网络一看拟合$\mu, \sigma^2$ 的任务, 心想: “采样得到的$Z$ 是包含噪声的, 重构起来多难啊, 我直接让方差$\sigma^2$ 学出个0来, 我学一个点的拟合肯定比学一个分布的拟合简单, 美滋滋”.

神经网络很容易过拟合, 把方差学成0, 那就坏了. 如果把样本重新映射回一个点, 那么VAE就直接退化回了AE. 所以我们还是希望$Z$ 是含有噪音的(方差不为0)的分布.

对于我们之前的假设$p(Z \mid X) \sim \mathcal{N}(\mu, \sigma^2)$ 要更严格, 不但要约束$\sigma^2 \neq 0$, 还要令方差不能太大, 也不能太小.

但如果假设$p(Z \mid X) \sim \mathcal{N}(0, I)$, 还保证了模型的生成能力:

$$
\begin{aligned}
p(Z) = & \sum_X p(Z \mid X) p(X) \\
= & \sum_x \mathcal{N}(0, I) p(X)\\
= & \mathcal{N}(0, I) \sum_X p(X) \\
= & \mathcal{N}(0, I)
\end{aligned}
$$

在该条件下$p(Z) \sim \mathcal{N}(0, I)$, 当脱离Encoder, 即不依靠输入样本$X$ 时, 我们可以直接从$\mathcal{N}(0, I)$ 中采样来生成可靠的结果.

我们直接使用KL散度来约束$p(Z \mid X)$, 令其服从标准正态分布.

KL散度(也称为相对熵)常用于度量两个分布之间的差异性, 假设$P$ 为样本真实分布, $Q$ 为模型预测的分布, 根据KL散度有:
$$
D_{\mathrm{KL}}(P \| Q)=\mathbb{E}_{\mathrm{x} \sim P}\left[\log \frac{P(x)}{Q(x)}\right]=\mathbb{E}_{\mathrm{x} \sim P}[\log P(x)-\log Q(x)]
$$
当$P, Q$ 越接近时, $D_{\mathrm{KL}}(P \| Q)$ 就越小, 当$P, Q$ 分布完全相同时, $D_{\mathrm{KL}}(P \| Q)$ 为0.
KL散度还有两个性质:
非负: KL散度是非负的.
不对称: 通常情况下, $D_{\mathrm{KL}}(P \| Q) \neq D_{\mathrm{KL}}(Q \| P)$, KL散度并不是真正意义上的距离.

求解过程如下:

$$
\begin{aligned}
&KL\Big(N(\mu,\sigma^2)\Big\Vert N(0,1)\Big)\\
=&\int \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2} \left(\log \frac{e^{-(x-\mu)^2/2\sigma^2}/\sqrt{2\pi\sigma^2}}{e^{-x^2/2}/\sqrt{2\pi}}\right)dx\\\
=&\int \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2} \log \left\{\frac{1}{\sqrt{\sigma^2}}\exp\left\{\frac{1}{2}\big[x^2-(x-\mu)^2/\sigma^2\big]\right\} \right\}dx\\\
=&\frac{1}{2}\int \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\mu)^2/2\sigma^2} \Big[-\log \sigma^2+x^2-(x-\mu)^2/\sigma^2 \Big] dx \\
=&\frac{1}{2}(-\log\sigma^2+\mu^2+\sigma^2-1)
\end{aligned}
$$

求解时, 需要最小化KL散度.

VAE常用的损失函数为:
$$
\begin{aligned}
\mathcal{L} = & \mathcal{L}_\mathrm{Recon} + \mathcal{L}_\mathrm{KL} \\
= & \mathcal{D}(\hat{X}_k,X_k)^2 + KL\Big(N(\mu,\sigma^2)\Big\Vert N(0,1)\Big)
\end{aligned}
$$
即重构损失和KL散度两部分.

梯度断裂 - 重参数

我们想要用梯度下降来优化$p(Z \mid X_k)$ 的均值$\mu$ 和方差$\sigma $, 但”采样”这个操作是不可导的, VAE利用重参数化技巧(Reparameterization Trick)使得梯度不因采样而断裂.

图片来自Variational autoencoders.

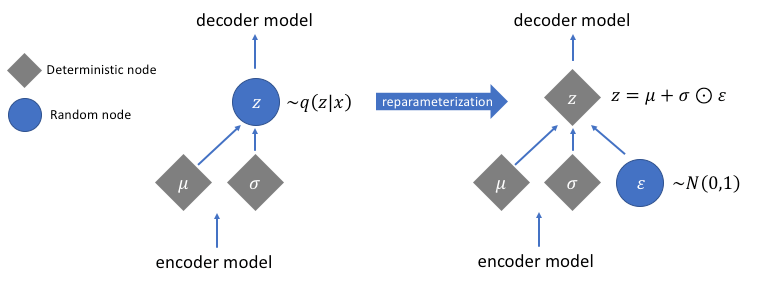
原理很简单, $Z$ 的导数可以写成:
$$
\begin{aligned}&\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(z-\mu)^2}{2\sigma^2}\right)dz \\
=& \frac{1}{\sqrt{2\pi}}\exp\left[-\frac{1}{2}\left(\frac{z-\mu}{\sigma}\right)^2\right]d\left(\frac{z-\mu}{\sigma}\right)
\end{aligned}
$$
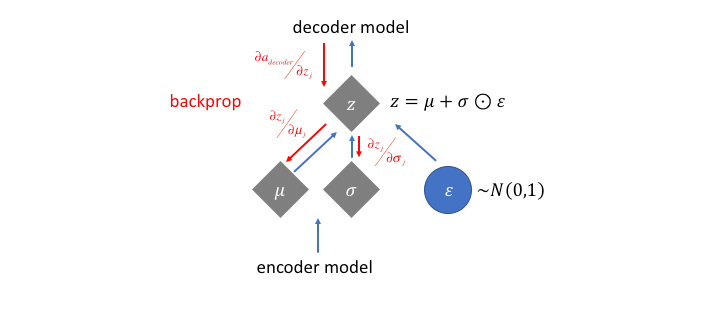
说明$(z - \mu) / \sigma^2 \sim \mathcal{N}(0, I)$, 从$\mathcal{N}(\mu, \sigma^2)$ 中采样, 就等价与从标准正态分布$\mathcal{N}(0, I)$ 中采样出一个$\epsilon$, 然后再通过$Z= \mu + \epsilon \times \sigma$ 缩放回去. 采样的导致梯度断裂的锅就丢给了$\epsilon$ 这个无关变量, 使得$\mu, \sigma^2$ 可以重新参与到梯度下降中优化: