本文前置知识:
- VAE基本原理: 详见变分自编码器入门.
Pytorch实现: VAE
本文是VAE的Pytorch版本实现, 并在末尾做了VAE的生成可视化.
本文的代码已经放到了Colab上, 打开设置GPU就可以复现(需要科学上网).
如果你不能科学上网, 应该看不到Open in Colab的图标.
Preparing
先导包:
import torch
from torch import nn
import torch.nn.functional as F
from torch import optim
from torch.utils.data import DataLoader
from torchvision import transforms
from torchvision.datasets import MNIST
import matplotlib.pyplot as pltVAE
CNN在MNIST上有过于明显的优势, 我们只采用纯DNN来做Auto Encoder.
随手搞一个网络结构出来就行:
- 输入层维度:
input_dim = 784. - 过渡层维度:
inter_dim = 256. - 隐变量维度:
latent_dim = 2, 方便后续可视化.
latent_dim = 2
input_dim = 28 * 28
inter_dim = 256
class VAE(nn.Module):
def __init__(self, input_dim=input_dim, inter_dim=inter_dim, latent_dim=latent_dim):
super(VAE, self).__init__()
elf.encoder = nn.Sequential(
nn.Linear(input_dim, inter_dim),
nn.ReLU(),
nn.Linear(inter_dim, latent_dim * 2),
)
self.decoder = nn.Sequential(
nn.Linear(latent_dim, inter_dim),
nn.ReLU(),
nn.Linear(inter_dim, input_dim),
nn.Sigmoid(),
)
def reparameterize(self, mu, logvar):
epsilon = torch.randn_like(mu)
return mu + epsilon * torch.exp(logvar / 2)
def forward(self, x):
org_size = x.size()
batch = org_size[0]
x = x.view(batch, -1)
h = self.encoder(x)
mu, logvar = h.chunk(2, dim=1)
z = self.reparameterize(mu, logvar)
recon_x = self.decoder(z).view(size=org_size)
return recon_x, mu, logvar说一点细节:
Encoder和Decoder用
nn.Sequential的形式写, 方便后续直接使用decoder.$p(Z\mid X_k)$ 的均值$\mu$ 和方差$\sigma^2$ 的形式上可以拆成两个小的DNN得出, 这里用一个DNN得出, 然后通过
torch.chunk函数将均值和方差分开, 实际上是和前者等价的.Encoder末尾千万别像网上某些例子在再接一个ReLU. 在优化过程中, 我们的隐变量$Z$ 是要逐渐趋向于$\mathcal{N}(0, I)$ 的, 如果非要加个ReLU的话, 本身假设的隐变量维度就很小, 小于0的隐变量直接就没了… Decoder在解码时直接就会因为信息不足而崩掉.
我们在这里拟合的是$\log \sigma^2$ 而不是$\sigma^2$, 所以重参数方差的表示法是
torch.exp(logvar / 2).
Loss
VAE的损失由重构损失和KL损失组成.
KL散度就不再推导了, 直接放结果:
$$
KL\Big(N(\mu,\sigma^2)\Big\Vert N(0,1)\Big)=\frac{1}{2}\Big(-\log \sigma^2+\mu^2+\sigma^2-1\Big)
$$
VAE的目标是最小化$Z$ 和$N(0, 1)$ 之间的KL散度, 代码只需要照着写就行了:
kl_loss = lambda mu, logvar: -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
recon_loss = lambda recon_x, x: F.binary_cross_entropy(recon_x, x, size_average=False)因为MNIST是黑白二值图像, 所以的Decoder就可以用Sigmoid后的值当做灰度, 重构损失直接就用BCE了, 用MSE做重构损失尚可. 但如果是三通道图像或者是灰度图像, 还是必须使用MSE做重构损失.
Training
先定义好训练的epoch和batch_size, 优化器随便选一个世界上最好的优化器Adam(lr=1e-3):
epochs = 100
batch_size = 128
transform = transforms.Compose([transforms.ToTensor()])
data_train = MNIST('MNIST_DATA/', train=True, download=False, transform=transform)
data_valid = MNIST('MNIST_DATA/', train=False, download=False, transform=transform)
train_loader = DataLoader(data_train, batch_size=batch_size, shuffle=True, num_workers=0)
test_loader = DataLoader(data_valid, batch_size=batch_size, shuffle=False, num_workers=0)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = VAE(input_dim, inter_dim, latent_dim)
model.to(device)
optimizer = optim.Adam(model.parameters(), lr=1e-3)训练的代码就不详细说了, 和一般的训练过程并无二异, 每次测试时最好把损失的两项都打印出来观察一下:
best_loss = 1e9
best_epoch = 0
valid_losses = []
train_losses = []
for epoch in range(epochs):
print(f"Epoch {epoch}")
model.train()
train_loss = 0.
train_num = len(train_loader.dataset)
for idx, (x, _) in enumerate(train_loader):
batch = x.size(0)
x = x.to(device)
recon_x, mu, logvar = model(x)
recon = recon_loss(recon_x, x)
kl = kl_loss(mu, logvar)
loss = recon + kl
train_loss += loss.item()
loss = loss / batch
optimizer.zero_grad()
loss.backward()
optimizer.step()
if idx % 100 == 0:
print(f"Training loss {loss: .3f} \t Recon {recon / batch: .3f} \t KL {kl / batch: .3f} in Step {idx}")
train_losses.append(train_loss / train_num)
valid_loss = 0.
valid_recon = 0.
valid_kl = 0.
valid_num = len(test_loader.dataset)
model.eval()
with torch.no_grad():
for idx, (x, _) in enumerate(test_loader):
x = x.to(device)
recon_x, mu, logvar = model(x)
recon = recon_loss(recon_x, x)
kl = kl_loss(mu, logvar)
loss = recon + kl
valid_loss += loss.item()
valid_kl += kl.item()
valid_recon += recon.item()
valid_losses.append(valid_loss / valid_num)
print(f"Valid loss {valid_loss / valid_num: .3f} \t Recon {valid_recon / valid_num: .3f} \t KL {valid_kl / valid_num: .3f} in epoch {epoch}")
if valid_loss < best_loss:
best_loss = valid_loss
best_epoch = epoch
torch.save(model.state_dict(), 'best_model_mnist')
print("Model saved")觉得Loss位数保留太多的可以自己设置.
下面画出训练过程中训练集和验证集上的损失曲线:
plt.plot(train_losses, label='Train')
plt.plot(valid_losses, label='Valid')
plt.legend()
plt.title('Learning Curve');训练曲线如下:
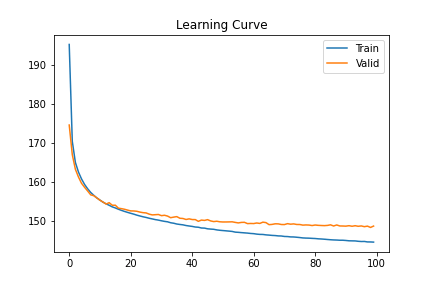
基本上Valid Loss稳定了(其实还有下降空间). 同时要保存在验证集上结果最好的模型, 因为等会还要用最好的模型做生成.
Visualization
再导俩包:
import numpy as np
from scipy.stats import normnorm可以在隐变量的区域内按照正态分布采样.
state = torch.load('best_model_mnist')
model = VAE()
model.load_state_dict(state)
n = 20
digit_size = 28
grid_x = norm.ppf(np.linspace(0.05, 0.95, n))
grid_y = norm.ppf(np.linspace(0.05, 0.95, n))
model.eval()
figure = np.zeros((digit_size * n, digit_size * n))
for i, yi in enumerate(grid_y):
for j, xi in enumerate(grid_x):
t = [xi, yi]
z_sampled = torch.FloatTensor(t)
with torch.no_grad():
decode = model.decoder(z_sampled)
digit = decode.view((digit_size, digit_size))
figure[
i * digit_size: (i + 1) * digit_size,
j * digit_size: (j + 1) * digit_size
] = digit
plt.figure(figsize=(10, 10))
plt.imshow(figure, cmap="Greys_r")
plt.xticks([])
plt.yticks([])
plt.axis('off');采样到$Z$ 后再给Decoder解码, 生成的结果如下:
 对于MNIST这样简单的数据集, 隐变量的某些区域已经能完成生成任务. 并且可以从图中观察到随着隐变量的变化对生成结果产生的影响.
对于MNIST这样简单的数据集, 隐变量的某些区域已经能完成生成任务. 并且可以从图中观察到随着隐变量的变化对生成结果产生的影响.从图中能够很明确的看到手写数字种类的过渡, 例如长的比较像的1, 9, 7, 都带圆弧的8, 3, 5, 再到6, 0. 但是VAE生成的内容有点点糊, 在MNSIT上影响不大, 但扩展到三通道数据时, 这个问题会变得更为显著.
Pokemon!
每个人都想做从零开始的宝可梦训练大师! 在李宏毅老师的课程中层提到过用VAE生成神奇宝贝的事情. 下面就来尝试下. 数据集下载点我, 原始数据大小为(3, 40, 40). 本节代码没有放到Colab上, 与在MNIST上的过程大同小异, 感兴趣可以自己尝试.
这次的VAE就该用CNN了, DNN有点力不从心.
下述代码不做过多的解读, 结果也不是太好, 大家就当看个乐子.
导包:
import os
import random
import matplotlib.pyplot as plt
import torch
import torch.nn.functional as F
from PIL import Image
from torch import nn
from torch import optim
from torch.utils.data import DataLoader, Dataset
from torchvision import transforms这次涉及到建立和读取图像数据集, 所以额外导了一些包.
然后建立图像数据集, 因为是无监督数据集, 所以比较简单:
class Pokemon(Dataset):
def __init__(self, image_paths, transform=None):
super(Pokemon, self).__init__()
self.image_paths = image_paths
if transform is not None:
self.transform = transform
def __len__(self):
return len(self.image_paths)
def __getitem__(self, item):
return self.transform(self.image_paths[item])数据集中实际上存储的是图像文件的路径, 在需要使用的时候再读出来, 我们将这一Pipeline集成在transform中.
接着定义CNN下的VAE:
latent_dim = 32
inter_dim = 128
mid_dim = (256, 2, 2)
mid_num = 1
for i in mid_dim:
mid_num *= i
class ConvVAE(nn.Module):
def __init__(self, latent=latent_dim):
super(ConvVAE, self).__init__()
self.encoder = nn.Sequential(
nn.Conv2d(3, 32, 3, 2, 1),
nn.BatchNorm2d(32),
nn.LeakyReLU(.2),
nn.Conv2d(32, 64, 3, 2, 1),
nn.BatchNorm2d(64),
nn.LeakyReLU(.2),
nn.Conv2d(64, 128, 3, 2, 1),
nn.BatchNorm2d(128),
nn.LeakyReLU(.2),
nn.Conv2d(128, 256, 4, 2, 1),
nn.BatchNorm2d(256),
nn.LeakyReLU(.2),
)
self.fc1 = nn.Linear(mid_num, inter_dim)
self.fc2 = nn.Linear(inter_dim, latent * 2)
self.fcr2 = nn.Linear(latent, inter_dim)
self.fcr1 = nn.Linear(inter_dim, mid_num)
self.decoder = nn.Sequential(
nn.ConvTranspose2d(256, 128, 4, 2),
nn.BatchNorm2d(128),
nn.LeakyReLU(.2),
nn.ConvTranspose2d(128, 64, 3, 2),
nn.BatchNorm2d(64),
nn.LeakyReLU(.2),
nn.ConvTranspose2d(64, 32, 3, 1),
nn.BatchNorm2d(32),
nn.LeakyReLU(.2),
nn.ConvTranspose2d(32, 32, 3, 1),
nn.BatchNorm2d(32),
nn.LeakyReLU(.2),
nn.ConvTranspose2d(32, 16, 3, 1),
nn.BatchNorm2d(16),
nn.LeakyReLU(.2),
nn.ConvTranspose2d(16, 3, 4, 2),
nn.Sigmoid()
)
def reparameterize(self, mu, logvar):
epsilon = torch.randn_like(mu)
return mu + epsilon * torch.exp(logvar / 2)
def forward(self, x):
batch = x.size(0)
x = self.encoder(x)
x = self.fc1(x.view(batch, -1))
h = self.fc2(x)
mu, logvar = h.chunk(2, dim=-1)
z = self.reparameterize(mu, logvar)
decode = self.fcr2(z)
decode = self.fcr1(decode)
recon_x = self.decoder(decode.view(batch, *mid_dim))
return recon_x, mu, logvar结构很随意, 主要是为了满足输入和解码后的大小相同.
定义Loss, 仍然是重构损失和KL损失:
kl_loss = lambda mu, logvar: -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
recon_loss = lambda recon_x, x: F.mse_loss(recon_x, x, size_average=False)重构损失使用MSE, 不能再使用BCE了, 因为RGB图像的数值不是二值的.
接下来是训练前的一些定义:
epochs = 2000
batch_size = 512
best_loss = 1e9
best_epoch = 0
valid_losses = []
train_losses = []
transform = transforms.Compose([
lambda x: Image.open(x).convert('RGB'),
transforms.ToTensor(),
])
root = "./pokemon"
image_paths = [os.path.join(root, x) for x in os.listdir(root)]
random.shuffle(image_paths)
train_image_paths = image_paths[: int(0.8 * len(image_paths))]
valid_image_paths = image_paths[int(0.8 * len(image_paths)): ]
pokemon_train = Pokemon(train_image_paths, transform=transform)
pokemon_valid = Pokemon(valid_image_paths, transform=transform)
train_loader = DataLoader(pokemon_train, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(pokemon_valid, batch_size=batch_size, shuffle=False)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = ConvVAE()
model.to(device)
optimizer = optim.Adam(model.parameters(), lr=1e-3)transform将图像从路径中读取出来, 并通过transforms.ToTensor转换为0, 1之间的RGB值.
然后就开始训练, 和在MNIST上的代码相同:
for epoch in range(epochs):
print(f"Epoch {epoch}")
model.train()
train_loss = 0.
train_num = len(train_loader.dataset)
for idx, x in enumerate(train_loader):
batch = x.size(0)
x = x.to(device)
recon_x, mu, logvar = model(x)
recon = recon_loss(recon_x, x)
kl = kl_loss(mu, logvar)
loss = recon + kl
train_loss += loss.item()
loss = loss / batch
optimizer.zero_grad()
loss.backward()
optimizer.step()
if idx % 100 == 0:
print(f"Training loss {loss: .3f} \t Recon {recon / batch: .3f} \t KL {kl / batch: .3f} in Step {idx}")
train_losses.append(train_loss / train_num)
valid_loss = 0.
valid_recon = 0.
valid_kl = 0.
valid_num = len(test_loader.dataset)
model.eval()
with torch.no_grad():
for idx, x in enumerate(test_loader):
x = x.to(device)
recon_x, mu, logvar = model(x)
recon = recon_loss(recon_x, x)
kl = kl_loss(mu, logvar)
loss = recon + kl
valid_loss += loss.item()
valid_kl += kl.item()
valid_recon += recon.item()
valid_losses.append(valid_loss / valid_num)
print(
f"Valid loss {valid_loss / valid_num: .3f} \t Recon {valid_recon / valid_num: .3f} \t KL {valid_kl / valid_num: .3f} in epoch {epoch}")
if valid_loss < best_loss:
best_loss = valid_loss
best_epoch = epoch
torch.save(model.state_dict(), 'best_model_pokemon')
print("Model saved")训练完VAE后, 对VAE学到的生成能力进行探索. 继续导入:
import numpy as np
from scipy.stats import norm因为这次隐变量维度latent_dim = 32, 不能再一次性的将所有维度采样看VAE的生成结果. 因此, 我打算选定一个维度和其他维度组合, 观察两两组合的维度产生的效果. 为了让结果更多变些, 我打算直接让其他隐变量也随机改变:
state = torch.load('best_model_pokemon')
model = ConvVAE()
model.load_state_dict(state)
n = 10
image_size = 40
grid_x = norm.ppf(np.linspace(0.05, 0.95, n))
grid_y = norm.ppf(np.linspace(0.05, 0.95, n))
model.eval()
selected = 21
coll = [(selected, i) for i in range(latent_dim) if i != selected]
for idx, (p, q) in enumerate(coll):
figure = np.zeros((3, image_size * n, image_size * n))
for i, yi in enumerate(grid_y):
for j, xi in enumerate(grid_x):
t = [random.random() for i in range(latent_dim)]
t[p], t[q] = xi, yi
z_sampled = torch.FloatTensor(t).unsqueeze(0)
with torch.no_grad():
decode = model.fcr1(model.fcr2(z_sampled))
decode = decode.view(1, *mid_dim)
decode = model.decoder(decode)
decode = decode.squeeze(0)
figure[:,
i * image_size: (i + 1) * image_size,
j * image_size: (j + 1) * image_size
] = decode
plt.title("X: {}, Y: {}".format(p, q))
plt.xticks([])
plt.yticks([])
plt.axis('off')
plt.imshow(figure.transpose(1, 2, 0))
plt.show()生成效果如下:

就是生成结果太糊了, 但能看出来左上角这玩意的轮廓明显像沼跃鱼没进化时候的水跃鱼:


右上角和左上角还有左下角可能生成的像个什么东西… 总体来说生成的效果不是很好, 非常糊, 看着感觉跟发育未完全的胚胎似的.
因为隐变量维数实在是太多了, 或许我们可以尝试更好点的办法, 找某一个神奇宝贝作为基准, 由编码器编码后得到一个现成的均值和方差, 然后再对某两个维度进行调整, 生成的结果会更贴近选定的神奇宝贝一些, 也就是使生成的结果更加合理一些.
只需要在生成隐变量时不再随机:
image_path = './pokemon/025MS.png'
with torch.no_grad():
base = transform(image_path).unsqueeze(0)
x = model.encoder(base)
x = x.view(1, -1)
x = model.fc1(x)
h = model.fc2(x)
mu, logvar = h.chunk(2, dim=-1)
z = model.reparameterize(mu, logvar)
z = z.squeeze(0)
for idx, (p, q) in enumerate(coll):
figure = np.zeros((3, image_size * n, image_size * n))
for i, yi in enumerate(grid_y):
for j, xi in enumerate(grid_x):
z[p], z[q] = xi, yi
z_sampled = torch.FloatTensor(z).unsqueeze(0)'
# ......下面相同的部分被我省略掉了. 我们选定皮卡丘作为基准, 生成结果如下:
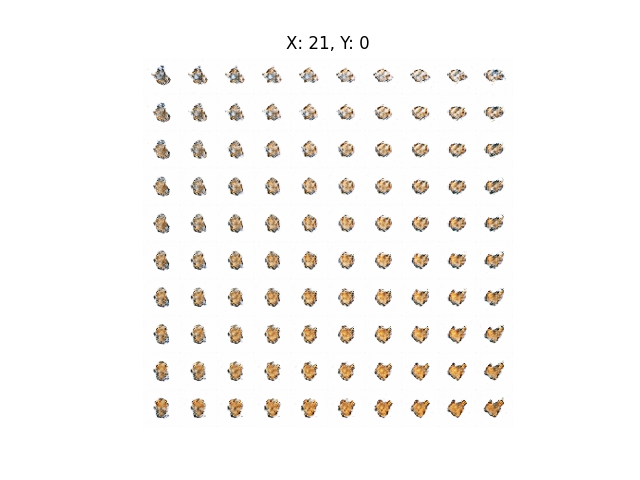

有时可以维持住皮卡丘的基本形状. 但随着某些隐变量的变化, 逐渐变得混沌, 甚至换了一个物种:

还是有点看不清, 如果裁剪图片到(3, 20, 20)效果可能会好一点, 重新搭建一种更小尺寸的VAE模型:
class ConvVAE(nn.Module):
def __init__(self, latent=latent_dim):
super(ConvVAE, self).__init__()
self.encoder = nn.Sequential(
nn.Conv2d(3, 32, 3),
nn.BatchNorm2d(32),
nn.LeakyReLU(.2),
nn.Conv2d(32, 64, 3),
nn.BatchNorm2d(64),
nn.LeakyReLU(.2),
nn.Conv2d(64, 128, 3),
nn.BatchNorm2d(128),
nn.LeakyReLU(.2),
nn.Conv2d(128, 128, 3, 2),
nn.BatchNorm2d(128),
nn.LeakyReLU(.2),
)
self.fc1 = nn.Linear(mid_num, inter_dim)
self.fc2 = nn.Linear(inter_dim, latent * 2)
self.fcr2 = nn.Linear(latent, inter_dim)
self.fcr1 = nn.Linear(inter_dim, mid_num)
self.decoder = nn.Sequential(
nn.ConvTranspose2d(128, 128, 3),
nn.BatchNorm2d(128),
nn.LeakyReLU(.2),
nn.ConvTranspose2d(128, 64, 3, stride=2),
nn.BatchNorm2d(64),
nn.LeakyReLU(.2),
nn.ConvTranspose2d(64, 32, 3),
nn.BatchNorm2d(32),
nn.LeakyReLU(.2),
nn.ConvTranspose2d(32, 16, 4),
nn.BatchNorm2d(16),
nn.LeakyReLU(.2),
nn.Conv2d(16, 3, 3),
nn.Sigmoid()
)然后向transform中添加裁剪:
transform = transforms.Compose([
lambda x: Image.open(x).convert('RGB'),
transforms.CenterCrop(20),
transforms.ToTensor(),
])将image_size设置为图像裁剪后的大小20, 其余代码全部不用动. 重新Train完模型, 我们依旧选择皮卡丘作为基准, 继续生成:

开始也能维持住皮卡丘的基本样貌, 但多了一丝混沌的气息. 随着其他隐变量的变化, 皮卡丘长得越来越像其他的生物:

继续演变, 甚至变成了右下角的某种东西:

感兴趣的可以自己Train一个模型, 自己探索一下. 结果不太好可能是我搭的模型有点太随意了…

