Knowledge Hypergraphs: Prediction Beyond Binary Relations
本文是论Knowledge Hypergraphs: Prediction Beyond Binary Relations的阅读笔记和个人理解.
Basic Idea
现有的知识图谱均以三元组的形式被存储, 即默认地将所有的关系以二元的形式表示. 但事实上, 在广为人知的FreeBase中, 有61%的关系都是非二元关系.
虽然现在有将多元关系转化为二元关系表示的方法, 但作者认为现有的KGE方法通过二元转换后做链接预测的效果都不是很好, 因为所有关系都被强假设为二元.
例如下图中描述的flies_between关系:
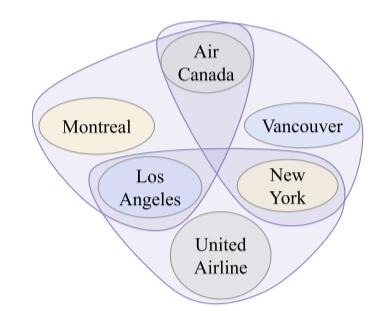
被现有的多元关系转二元关系技术分解为如下形式:
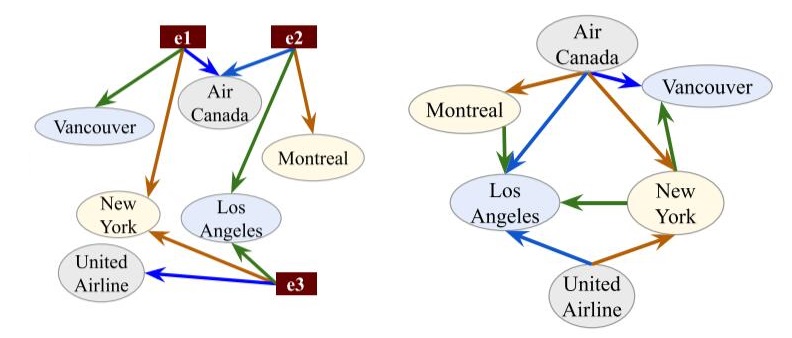
左侧转换并没有损失信息, 但添加了三种额外的实体.
右侧转换可能存在歧义, 转换后以二元关系的形式存在, Air Canada, Montreal, Los Angeles, 之间存在关系flies_between是合理的, 但单独看Air Canada, New York, Los Angeles也存在关系flies_between. 参考原图, Air Canada不可能从New York飞到Los Angeles, 但
因此, 作者希望提出基于超图的多元关系Knowledge Embedding方法.
Hypergraph
首先来介绍一下超图.
超图被描述为$H=(X, E)$, $X$ 是一个有限集合, 其中的元素被称为节点或顶点, $E$ 为$X$ 的非空子集, 被称为超边或连接.
下面展示一个例子:
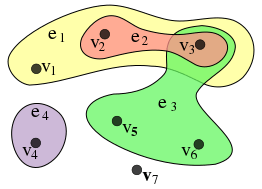
图片出自维基百科.
在该超图中, 有:
$$
\begin{aligned}
X&=\{v_1, v_2, v_3, v_4, v_5, v_6, v_7\} \\\ \\
E&=\{e_1, e_2, e_3, e_4\}\\
&=\{\{v_1, v_2, v_3\}, \{v_2, v_3\}, \{v_3, v_5, v_6\}, \{v_4\}\}
\end{aligned}
$$
对于我们所熟知的图而言, 边只能与两个顶点相连. 在超图的体系下, 边称之为超边, 能够与任意个数的顶点相连, 普通图只是在超图中的一种每条边节点数量均为2的特殊情况, 因此, 超图理论与普通图是兼容的.
而Hypergraph本身结构的高度灵活性, 对于相同的现实生活中的场景, 可能有不同的描述方法和建模方法.
Knowledge HyperGraph Completion
如何把Knowledge Graph Completion扩展到超图中?
现实世界的实体集为$\mathcal{E}$, 有限关系集为$\mathcal{R}$, 区别在于超图中的元组不再是三元组, 而是可以容纳更多实体的元组$\tau = r(e_1, e_2, \dots, e_k), r\in \mathcal{R}, e_i \in \mathcal{E}$.
在超图中, 每条超边就是一个$\tau$, $|r|$ 为关系$r$ 所对应的实体数量, 可以设置为固定的.
我们所构建的知识超图应该是真实世界元组$\tau$ 的一个子集$\tau ^ \prime \subseteq \tau$, Knowledge HyperGraph Completion的目标就是利用$\tau ^ \prime$ 找到缺失的真实知识$\tau \backslash \tau^\prime$.
HypE
作者先定义了$\odot(\cdot)$ 为向量的逐元素点乘求和(其实就是向量内积):
$$
\odot\left(\mathbf{v}_{\mathbf{1}}, \mathbf{v}_{\mathbf{2}}, \ldots, \mathbf{v}_{\mathbf{k}}\right)=\sum_{i=1}^{\ell} \mathbf{v}_{\mathbf{1}}{ }^{(i)} \mathbf{v}_{\mathbf{2}}{ }^{(i)} \ldots \mathbf{v}_{\mathbf{k}}^{(i)}
$$
$\mathbf{v}_j^{(i)}$ 为$\mathbf{v}_j$ 的第$i$ 个元素.
HSimplE
在SimplE中, 通过学习到实体$e$ 分别在头实体和尾实体的两个不同位置的嵌入$\mathbf{e}^{(1)}, \mathbf{e}^{(2)}$, 和关系及其逆关系的嵌入$\mathbf{r}^{(1)}, \mathbf{r}^{(2)}$ 来求得三元组是否为真的得分:
$$
\phi\left(r\left(e_{1}, e_{2}\right)\right)=\odot\left(\mathbf{r}^{(\mathbf{1})}, \mathbf{e}_{\mathbf{1}}^{(\mathbf{1})}, \mathbf{e}_{\mathbf{2}}^{(\mathbf{2})}\right)+\odot\left(\mathbf{r}^{(\mathbf{2})}, \mathbf{e}_{\mathbf{2}}^{(\mathbf{1})}, \mathbf{e}_{\mathbf{1}}^{(\mathbf{2})}\right)
$$
作者认为, SimplE的核心在于将三元组形式中实体可能位于任何位置的表示方式都考虑到了, 作者在这种启发下将SimplE扩展到了超图上.
在超图中, 超边能连接任意数量的顶点, 我们不可能将每个实体在每个位置上都单独学习一个Embedding, 所以我们应该用一个单独的向量来代替, 而不是像SimplE一样使用多个向量.
作者认为, 只使用单个$\mathbf{e}$ 能够被视为$\alpha$ 个不同位置出现的实体嵌入的拼接, 例如$\mathbf{e}=\operatorname{concat}(\mathbf{e}^{(\mathbf{1})} + \mathbf{e}^{(\mathbf{2})})$.
我认为只要保证同实体在不同位置上的表示足够不同, 就能使用单个$\mathbf{e}$.
作者使用了一个迂回的方法, 既然不能学习所有位置, 就简单的通过平移操作来改变不同位置上同一实体的表示. 每个实体的表示因位置不同而产生变化, 那么在元组$\tau$ 中, 打分函数为:
$$
\begin{aligned}
\phi\left(r\left(e_{i}, e_{j}, \ldots, e_{k}\right)\right) &=\odot\left(\mathbf{r}, \mathbf{e}_{\mathbf{i}}, \operatorname{shift}\left(\mathbf{e}_{\mathbf{j}},
\operatorname{len}\left(\mathbf{e}_{\mathbf{j}}\right)\cdot\frac{1} {\alpha}\right), \ldots,\right.
\left.\left.\operatorname{shift}\left(\mathbf{e}_{\mathbf{k}}, \operatorname{len}\left(\mathbf{e}_{\mathbf{k}}\right) \cdot\frac{(\alpha-1)} { \alpha}\right)\right)\right)
\end{aligned}
$$
其中$\alpha=|r|$ , $\text{shift}(\mathbf{v}, x)$ 代表将$\mathbf{v}$ 向左平移$x$ 个单位, 并将多余的部分补到右侧(参考源码).
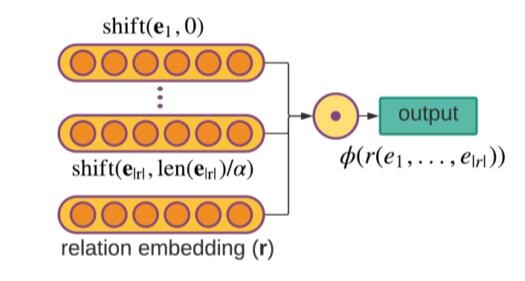
HypE
HSimplE的平移操作有点太简单了, 把HSimplE的Shift操作换成了卷积就是HypE.
对于实体$e$ 在关系$r$ 中可能存在的每个位置$i$, 都有卷积核$\omega$ 对实体的Embedding $\mathbf{e}$ 提取特征:
$$
f(\mathbf{e}, i)=\operatorname{concat}\left(\mathbf{e} \ast \omega_{\mathrm{i} 1}, \ldots, \mathbf{e} \ast \omega_{\mathrm{in}}\right) \mathrm{P}
$$
其中$P$ 为投影矩阵. $n$ 为卷积核个数, 即在位置$i$ 上有$n$ 个不同的卷积核提取特征, 再将它们拼接到一起, 最后投影回某个维度:

和HSimplE相似, 把关系嵌入, 不同位置上的不同实体嵌入在一起点乘, 作为元组得分:
$$
\phi\left(r\left(e_{1}, \ldots, e_{|r|}\right)\right)=\odot\left(\mathbf{r}, f\left(\mathbf{e}_{\mathbf{1}}, 1\right), \ldots, f\left(\mathbf{e}_{|\mathbf{r}|},|r|\right)\right)
$$
即:

作者认为, 使用位置特化的卷积核好处有二:
- 由于实体Embedding的位置信息是由卷积核额外添加进去的, 而非包含于实体Embedding本身, 所以更利于实体Embedding变得与位置无关.
- 位置和实体的分离使得HypE能作用于任意数量实体的Knowledge base, 这额外给予了HypE更多的鲁棒性, 即使遇到从未见过的实体, 也能有点用处.
Objective Function and Training
HSimplE和HypE都使用小批量梯度下降训练.
负例的生成是由TransE负例生成的思路扩展到超图而来, 对于每个元组, 生成$N|r|$ 个负例, $N$ 为负样本生成率(超参).
损失函数采用交叉熵(实际上应该是温度为1的InfoNCE, 但原文写的CE, 这里暂时尊重一下原文), 最大化正例元组的打分, 最小化负例元组的打分:
$$
\mathcal{L}(\mathbf{r}, \mathbf{e})=\sum_{x^{\prime} \in \tau_{\text {train }}^{\prime}}-\log \left(\frac{e^{\phi\left(x^{\prime}\right)}}{e^{\phi\left(x^{\prime}\right)}+\sum_{x \in T_{n e g}\left(x^{\prime}\right)} e^{\phi(x)}}\right)
$$
$x$ 为所有训练集, 验证集, 测试集元组$\tau^\prime$ 的某个元组, $\tau ^ \prime_\text{train}$ 为训练集, $T_{neg}(x^\prime)$ 为生成的负例.
Experiments
详细的参数设置请参照原论文.
Dataset
JF - 17K是前人提出的数据集, 但没有验证集, 作者随机选了20%作为验证集.
此外, 作者从FreeBase中创建了新的数据集FB - AUTO, M - FB15K. 详细的数据集创建请参考原论文附录部分. 它们的统计信息如下:
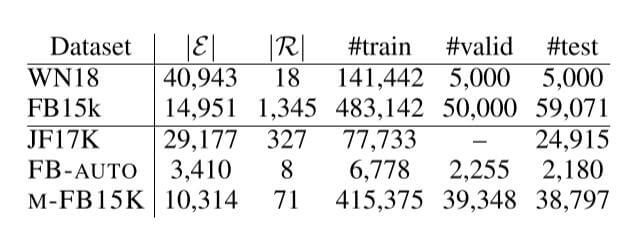
Baseline
因为在超图补全上的模型很少, 所以需要抓一些之前的方法扩展到超图情况:
- 对于处理二元关系的方法, 作者将其扩展到更多实体的情况, 如r - SimplE, m - DistMult, m - CP.
- 也有一些不用扩展的方法, 能直接处理更多实体, 如m - TransH.
Knowledge HyperGraph Completion Results
HypE在这几个超图补全数据集上结果如下:

HypE相较于其他方法有显著提升.
因为位置特化的卷积核能将实体本身的信息和位置信息解耦, 所以作者认为HypE应该具有更高的参数利用率. 作者做了MRR随Embedding Dimensionss变化的曲线, 结果如下:
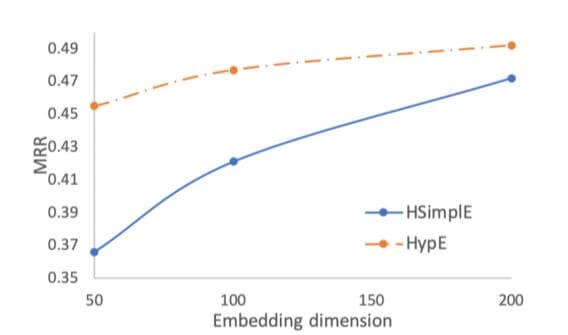
HypE在200维度以下时, 是完全优于Baseline HSimplE的.
HypE使用了位置特化的卷积核, 应该能处理更多实体出现在不同位置上的情况, 作者创建一个缺失位置的测试集, 其中的每个元组至少有一个实体在某个位置没有出现过, 这种情况更具挑战性. 与其他方法对比结果如下:
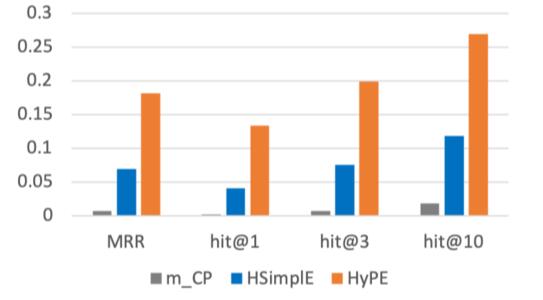
其他方法在缺失位置信息的情况下表现很差, 相较来说HypE确实能处理更多这种挑战性的情况, 也表明HypE确实受益于位置和实体信息解耦的设计.
Knowledge Graph Completion Results
在现有的三元组形式数据集WN18和FB15k上结果如下:
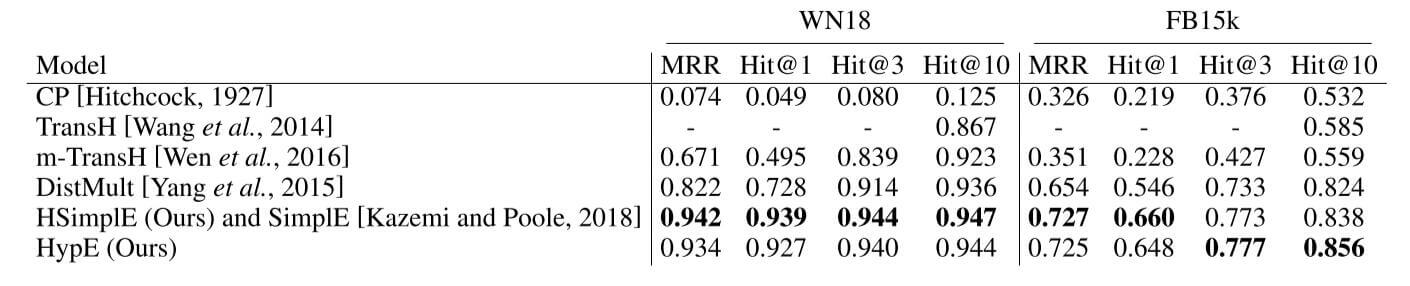
HSimplE取得了相当好的表现, HypE也与其相似.
由于这两个数据集上包含大量的逆关系导致Data Leakage存在, 使用WN18RR和FB15k-237更有说服力. 但这个实验说明面向超图的任务优化有希望提升三元组形式的数据集链接预测性能.
Ablation Study on Different Arities
作者还在JF17K上将超边设置为不同的实体数量, 结果如下:
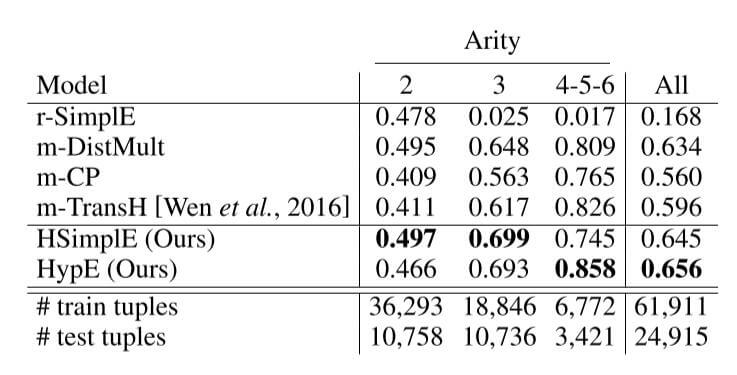
超边实体数量比较多时, HSimplE表现相较于HypE来说并不好, 超边实体数量较少时, HSimplE效果比HypE稍好. 总体上来说作者提出的两种方法效果略好.
Summary
在知识超图上的研究还比较少, 本文提出了在超图架构下的两个新数据集, 并给出了将处理三元组KGE问题迁移到超图框架下的方法.
其实与某些图游走方法的想法有一些相似之处, 显式指明多实体之间存在的关系, 而非只考虑两实体, 这些额外的附加信息可以帮助推理. 但图游走类算法更加随意, 在知识超图上的游走仅限于同关系下的实体集.
总感觉这篇论文有哪块没理解, 尤其是附录, 有机会回看.
