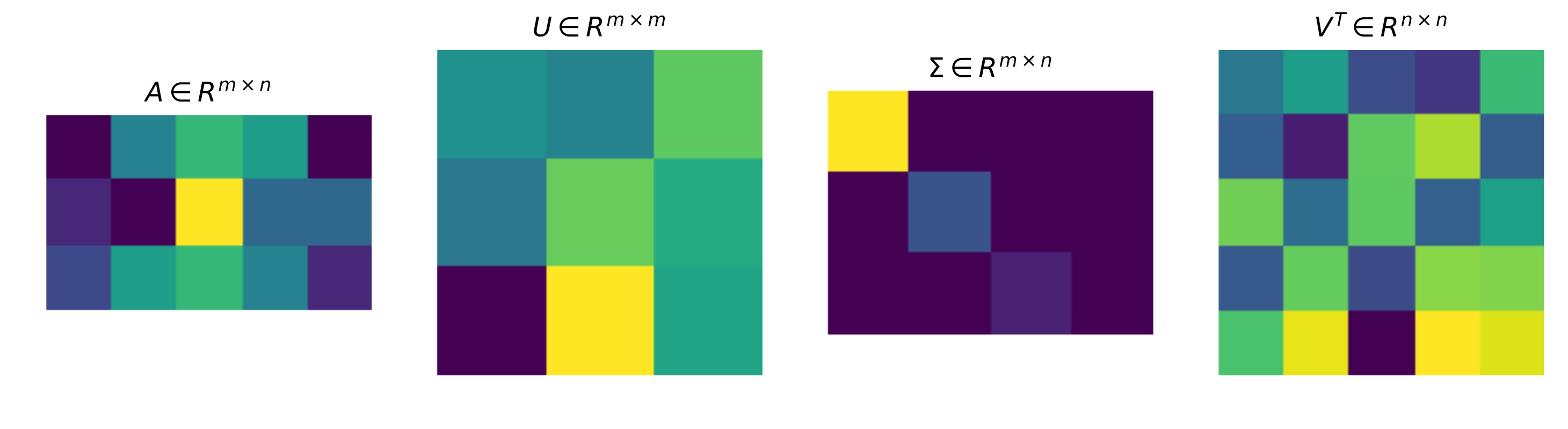
奇异值分解SVD Singular Value Decomposition

SVD(Singular Value Decomposition) 是一种基于原矩阵进行分解的特征分解手段. 主要是用小的多的数据来表示原始的数据集, 实质是对数据的过滤和去噪.

先说一下特征值分解, 对与$A_{n\times n}$ 能够以如下方式进行特征值的分解, $Q$ 为特征向量矩阵, 但这种方式仅限于方阵的分解. 当对任意大小的矩阵都生效时, 就有了SVD.
$$
A = Q\Sigma Q^T=
Q\left[
\begin{matrix}
\lambda_1 & \cdots & \cdots & \cdots\\
\cdots & \lambda_2 & \cdots & \cdots\\
\cdots & \cdots & \ddots & \cdots\\
\cdots & \cdots & \cdots & \lambda_m
\end{matrix}
\right]Q^T
$$
SVD同样也是对特征值的分解, 但是SVD不要求被分解的矩阵为方阵. 假设$A_{m\times n}$, $U_{m\times m}$, $V_{n\times n}$, $\Sigma_{m\times n}$. 其中$U$, $V$ 均为标准的正交矩阵. 它有如下性质:
$$
U^TU = I = V^TV
$$

$\Sigma$ 是对角阵, 且对角线上的每个元素都称为奇异值, 一般形式如下:
$$
\Sigma =
\left[
\begin{matrix}
\sigma_1 & 0 & 0 & 0 & 0\\
0 & \sigma_2 & 0 & 0 & 0\\
0 & 0 & \ddots & 0 & 0\\
0 & 0 & 0 & \ddots & 0
\end{matrix}
\right]_{m\times n}
$$

如果我们将$A$ 和 $A^T$ 做乘法, 就能得到满足 $U$ 大小的方阵, 就能够进行特征值分解. 所得到的的$m$ 个特征值对应的特征向量的张成就是矩阵$U$. 并将其中每个特征向量成为$A$ 的左奇异向量. 即:
$$
AA^Tu_i = \lambda_iu_i
$$
同理, 将$A^T$和$A$ 做乘法, 可以得到满足$V$ 大小的方阵. 称其为右奇异矩阵.
$$
A^TAv_i = \lambda_iv_i
$$
如何求出$\Sigma$ 呢? 由于除去它对角线上的奇异值其他位置都是0, 所以只需要求出每个奇异值.
$$
\displaylines{
A = U\Sigma V^T \Rightarrow AV = U\Sigma V^TV \Rightarrow AV = U\Sigma \\
Av_i = \sigma_i u_i \\
\sigma = \frac{Av_i}{u_i}}
$$
这样求很麻烦, 不如直接用我们已知的条件:
$$
\begin{aligned}
A &= U\Sigma V^T \\
A^T &= V\Sigma U^T \\
A^TA &= V\Sigma U^TU\Sigma V^T \\
&= V \Sigma ^2 V^T
\end{aligned}
$$
能够看到最后求出来的等式直接能得到:
$$
\sigma_i = \sqrt{\lambda_i}
$$
对于奇异值, 在奇异值矩阵中从大到小排列, 很多时候前10%甚至1%的奇异值占到了全部奇异值之和的99%. 所以我们能用最大的$k$个奇异值和对应的左右奇异向量来近似描述矩阵.
$$
A_{m\times n} = U_{m \times m} \Sigma_{m\times n}V^T_{n\times n} \approx U_{m \times k} \Sigma_{k\times k}V^T_{k\times n}
$$