集成学习 Ensemble Learning
Boosting, Bagging, Stacking都是集成学习的方式, 都是考虑用多个弱学习器通过某种方式集合在一起, 形成一个泛化性能更强的强学习器.
Boosting
Boosting是一种通过组合同质弱学习器来顺序学习产生强学习器的通用且有效的方法, 最早出现在AdaBoost, 它的启发来自于管委员会中每个成员只提供一些不成熟的判断, 但整个委员会却产生较为准确的决策. 弱学习器在一起做的决策共同做决策, 仍然可以得到一个不错的结果. Adaboost让每次迭代对每个样本都维护一个权重分布, 权重较大的误分类样本会比权重较小的误分类样本贡献更大的训练错误率. 为了获得更小的加权错误率, 弱分类器必须更多的聚焦于高权重的样本, 保证对它们准确的预测.

每次训练一个新的弱学习器, 误差为最小加权训练误差, 每一轮提高分类错误的样本权重, 降低分类正确的样本权重. 并且每次训练的目标是找到一个函数来拟合上一轮的残差(实际观察值与估计值之差). 代表算法Adaboost(Adaptive Boosting).
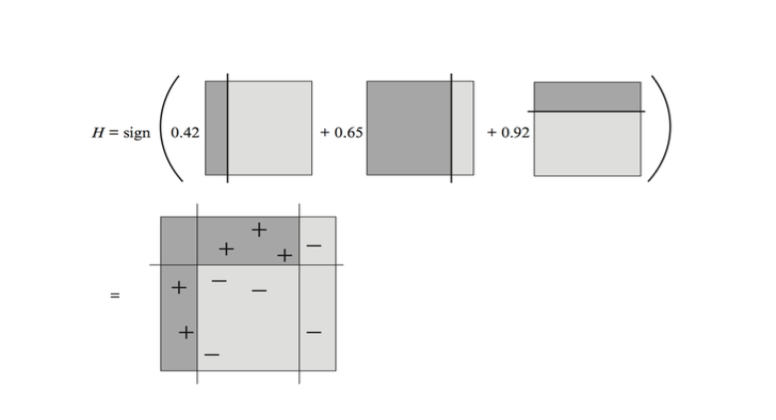
Bagging
Bagging(Bootstrap aggregating)并行训练多个同质弱学习器, 在取数据集时使用Boostrap(自助法). 自助法的意思是指在每次训练新的弱学习器时, 都从数据集中做放回抽样, 这样其他训练器在训练时也可能抽到相同的样本.
Boostrap就是一个在自身样本重采样的方法来估计真实分布的问题, 在不知道实际分布时, boostrap十分有用. 举个Boostrap的例子:
假设一下, 第一次重新捕鱼100条, 发现里面有标记的鱼12条, 记下为12%, 放回去, 再捕鱼100条, 发现标记的为9条, 记下9%, 重复重复好多次之后, 假设取置信区间95%, 你会发现, 每次捕鱼平均在10条左右有标记, 所以, 我们可以大致推测出鱼塘有1000条左右. 其实是一个很简单的类似于一个比例问题. 这也是因为提出者Efron给统计学顶级期刊投稿的时候被拒绝的理由–”太简单”. 这也就解释了, 为什么在小样本的时候, bootstrap效果较好, 你这样想, 如果我想统计大海里有多少鱼, 你标记100000条也没用啊, 因为实际数量太过庞大, 你取的样本相比于太过渺小, 最实际的就是, 你下次再捕100000的时候, 发现一条都没有标记, 这就很尴尬了.
回来说Bagging, 重复抽样和训练这个过程许多次, 就能获得很多同质的弱学习器. 最后在进行预测时采用投票机制, 所有弱分类器共同投票得出结果. 代表算法随机森林就是这样具有了很强的鲁棒性.

Bagging和Boosting的区别
人们常常把Bagging和Boosting混淆, 其实这两个种集成是完完全全不同的.
| Bagging | Boosting | |
|---|---|---|
| 样本选择 | 有放回抽样, 训练集每次都不同 | 训练集每次相同, 但在分类器中权重不同 |
| 样本权重 | 权重一致 | 不断调整, 错误率越大权重越高 |
| 预测权重 | 投票得出, 权重相等 | 错误率高的学习器比重小 |
| 并行计算 | 独立并行计算 | 只能串行, 每次新学习器需要上个学习器的结果 |
| 优化方向 | 方差, 即降低过拟合 | 偏差, 即降低欠拟合 |
- Bagging + 决策树 = 随机森林
- AdaBoost + 决策树 = 提升树
- Gradient Boosting + 决策树 = GBDT
Stacking
Stacking就比较特殊了, 前面二者都是基于样本的, 而Stacking是基于模型的组合. Stacking是在原有的模型预测结果上, 再重新训练一个模型, 就仿佛在原来的模型上进行”堆叠” 一个模型, 这样做能够从不同模型中提取出不同信息. 由于不同的特征, 可能不同类型的模型会在不同特征上有不同的预测效果, Stacking可以取其精华弃其糟粕, 舍弃它们不好的预测部分, 从而达到提升效果的目的.
对于Stacking来讲, 使用不同算法的模型可以增强效果, 在不同数据上训练得来的模型也可以增强效果.
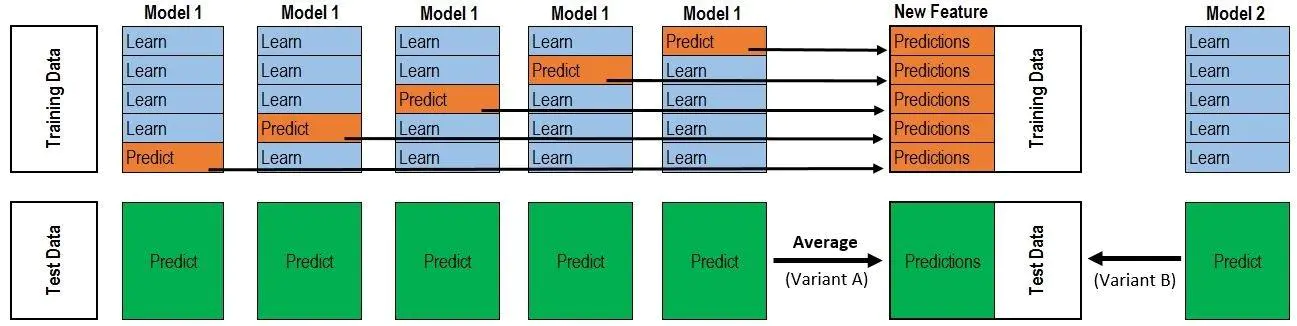
根据上图, 比如已知数据集的大小为1000, 训练时应该遵循如下流程:
- 取一个模型$\rm Model_1$, 对$\rm Model_1$做5折交叉验证, 得到5个用不同部分数据训练出的同质模型, 每次使用的训练集样本数量应该为800, 验证集样本数量为200.
- 提取每个同质模型中对验证集的预测结果(大小为200)作为堆叠的下一个模型$\rm Model_{next}$的数据集的一部分, 因为有5折交叉验证, 所以将五个$200\times 1$ 的数据拼起来得到的$1000\times 1$的数据集. 同时标签也拼接到这刚好和总共的数据集大小一致.
- 如果还有其他的模型作为第一层的模型, 那么将它们对自己验证集的结果拼接起来, 形成$1000\times n$的数据集作为下一层模型的训练数据.
- 反复执行.
理解了训练过程, 测试过程就很简单了. 假设测试集是不包含在已知数据集的独立集合, 在每次每个分类器对全部的数据进行预测, 假设是5折交叉验证产生的分类器, 则对5个分类器得到的预测结果直接取平均, 得到同样测试集大小的测试集数据, 然后递交给下一层.
如果上述文字描述还不够直观, 那么下面这个图很好的说明了Stacking的工作过程(出自【机器学习】Stacking方法详解):


