卷积神经网络 Convolutional Neural Network
卷积神经网络是一种含有空间信息的数据表示方法. 它与普通的DNN不同, 它包含了数据的位置信息, 以保证每次看到的是数据矩阵的一个区域, 而不是单纯的矩阵某一维. 卷积神经网络里所说的”卷积”并非真正意义上的卷积运算, 而是互相关运算. 下面这个是VGG16, 算早期CNN的先驱之一了. 用了很多小的卷积核, 网络也比较深(相对之前的来说).
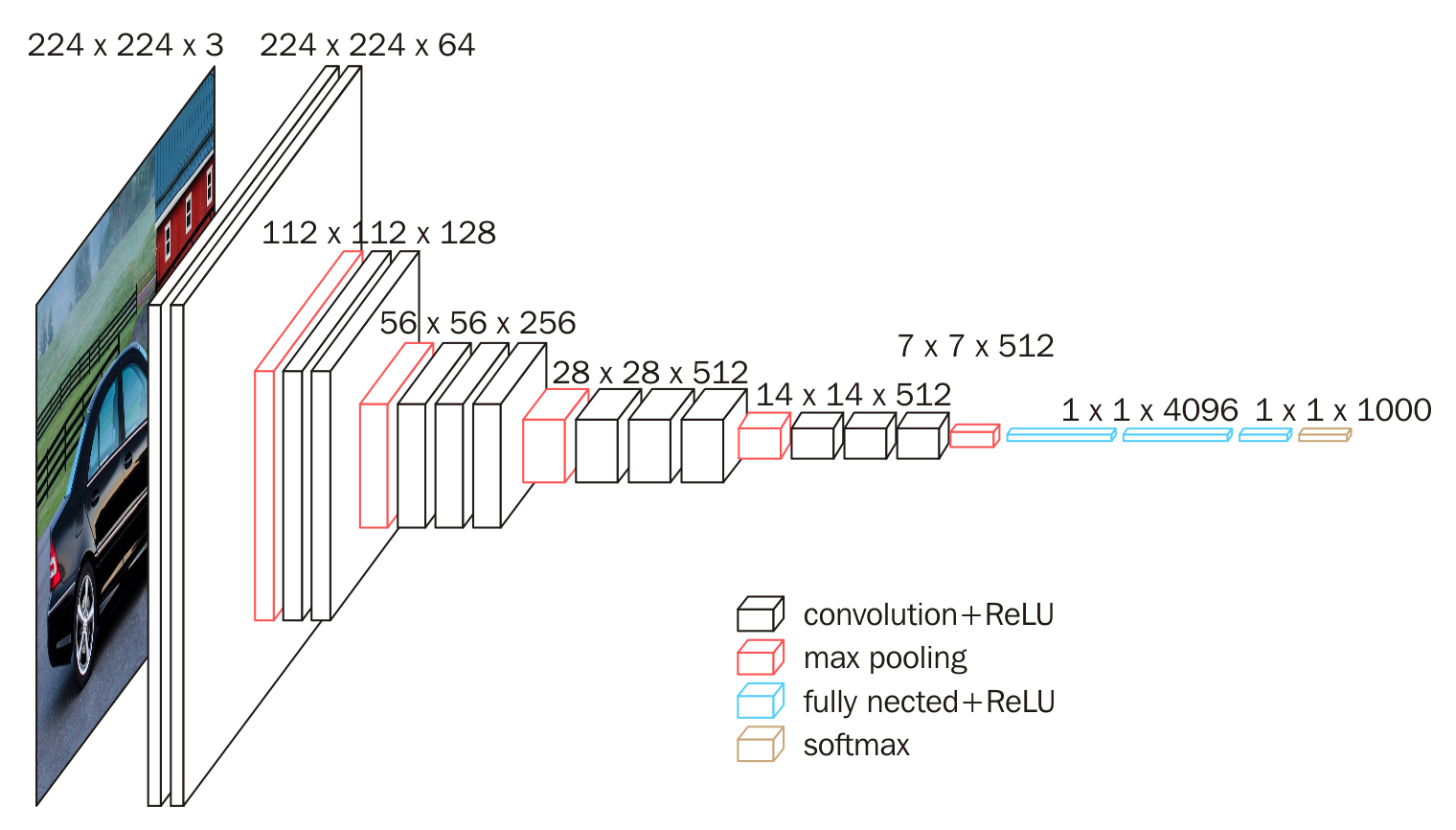
从图中能看到, 卷积神经网络就是将数据从短而粗, 变为长而细. 也就是从原始数据表征, 通过复杂的神经元连接转换为人们难以理解, 高度抽象的特征. 这类特征往往是通过多次学习得来的, 但效果也非常好.
卷积层 Convolutional Layer
每个卷积层由若干个卷积核和一个偏置$b$组成, 每一个卷积核和输入数据相互作用可以得到一张特征图. 卷积层的反向传播方式与DNN反向传播完全一致.
卷积核 Filter
以二维为例子, 卷积核(也叫滤波器)就是一个含有过滤信息的滑动窗口, 在二维平面上不断滑动, 卷积核内的权重是学习得来的, 它与原数据进行”卷积”运算(其实叫点积求和运算更合适), 就是对应位置相乘最后加到一起, 形成这个卷积核在这个位置上得到的数据, 将数据仍然以矩阵的形式拼接, 这个矩阵就称为特征图. 在卷积过程之中, 卷积核的参数不会发生改变, 这叫做权值共享. 也就是一个卷积核提取了原图不同位置的相同特征. 所以引入多个卷积核就能提取原图中的不同特征.
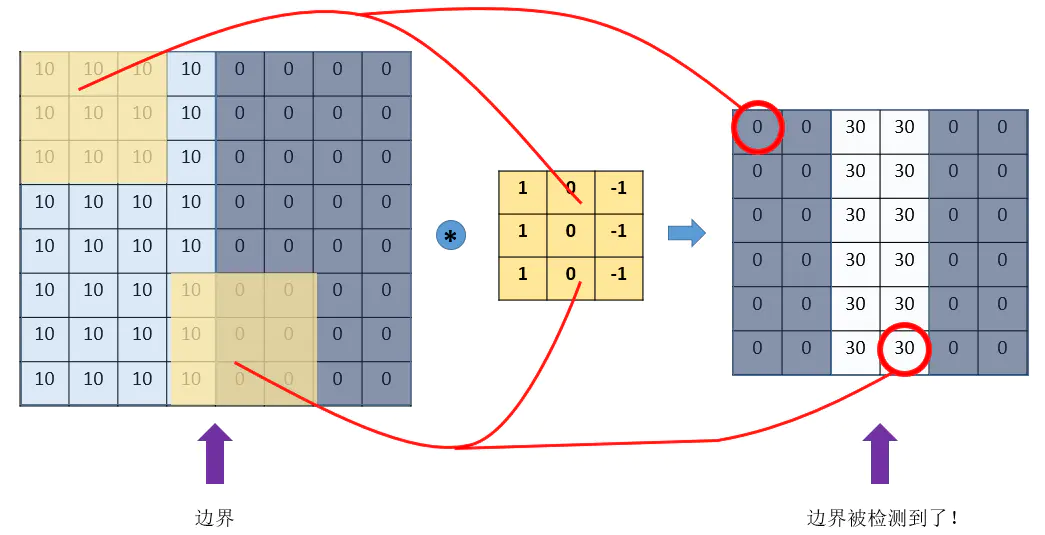
在这里左上角的元素是$[10\times 1 + 10\times 0 + 10\times(-1)]\times3=0$, 中间下方的元素是$[10\times 1+0\times0+0\times-1]\times3=10$. 如果写成一个抽象的公式, 在二维情况下:
$$
C(x, y)=\sum_{t=-\infty}^\infty\sum_{s=-\infty}^\infty F(s, t)\times G(x-s, y-t)\Delta s\Delta t
$$
每个卷积核进行运算时, 是贯穿所有维的.
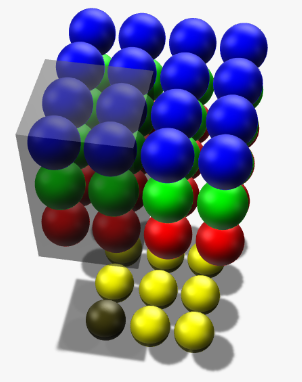
比如图中的运算, 上方的输入的RGB图像数据大小为$4\times4\times3$, 卷积核所对应的最后一维也就是深度一定会和输入数据一致, 也就是$2\times2\times3$. 所以但是深度上卷积核并不共享权重, 每层深度用的是自己的权重. 对于$R, G, B$三个通道第$i$个位置上的输入数据分别为$x_{ri}, x_{gi}, x_{bi}$, 卷积核中的对应权重有$w_{ri}, w_{gi}, w_{bi}$, 有如下形式:
$$
\begin{bmatrix}
w_{r1} & w_{r2} \\
w_{r3} & w_{r4}
\end{bmatrix},
\begin{bmatrix}
w_{g1} & w_{g2} \\
w_{g3} & w_{g4}
\end{bmatrix},
\begin{bmatrix}
w_{b1} & w_{b2} \\
w_{b3} & w_{b4}
\end{bmatrix}
$$
和深度神经网络一样, 每个卷积核都有一个权重. 那么当计算特征图的时候, 第$k$ 个卷积核对应的特征图每个位置的输出$y_k$ 其实是将深度维上的对应位置的所有结果加起来(别忘了偏置$b_k$, 因为前面卷积运算计算完以后是一个数, 而非一个矩阵, 所以$b_k$ 也是一个数).
$$
y_k = \begin{bmatrix}w_{r1} & w_{r2} &w_{r3} & w_{r4}\end{bmatrix}\cdot\begin{bmatrix}x_{r1} \\ x_{r2} \\x_{r3} \\ x_{r4}\end{bmatrix}+\begin{bmatrix}w_{g1} & w_{g2} &w_{g3} & g_{r4}\end{bmatrix}\cdot\begin{bmatrix}x_{g1} \\ x_{g2} \\x_{g3} \\ x_{g4}\end{bmatrix}+\begin{bmatrix}w_{b1} & w_{b2} &w_{b3} & w_{b4}\end{bmatrix}\cdot\begin{bmatrix}x_{b1} \\ x_{b2} \\x_{b3} \\ x_{b4}\end{bmatrix}+b_k
$$
在计算完后, 将filters的所有结果一层层的叠加起来, 就使得新的数据又拥有了深度.
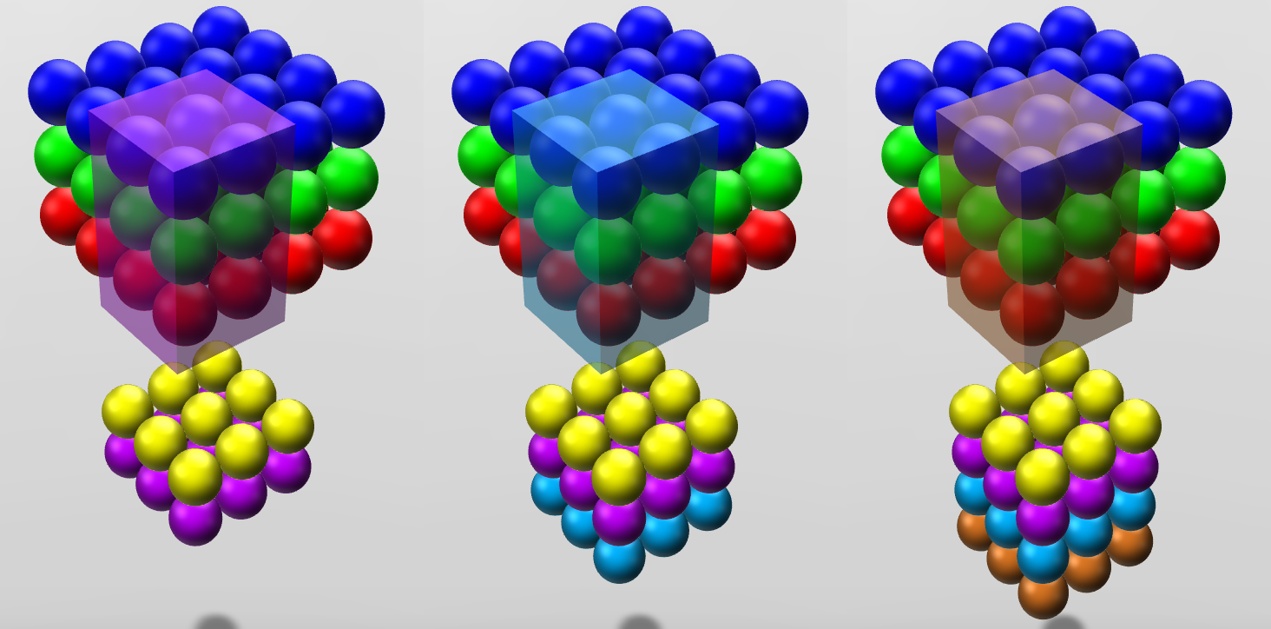
图中经过四个卷积核扫描输入空间后, 得到了四个$3\times3\times1$的输出. 也就是$3\times3\times4$的输出. 由此可见卷积层有多少卷积核, 就有多深. 我们当然不能忘记激活函数, 加上激活函数:
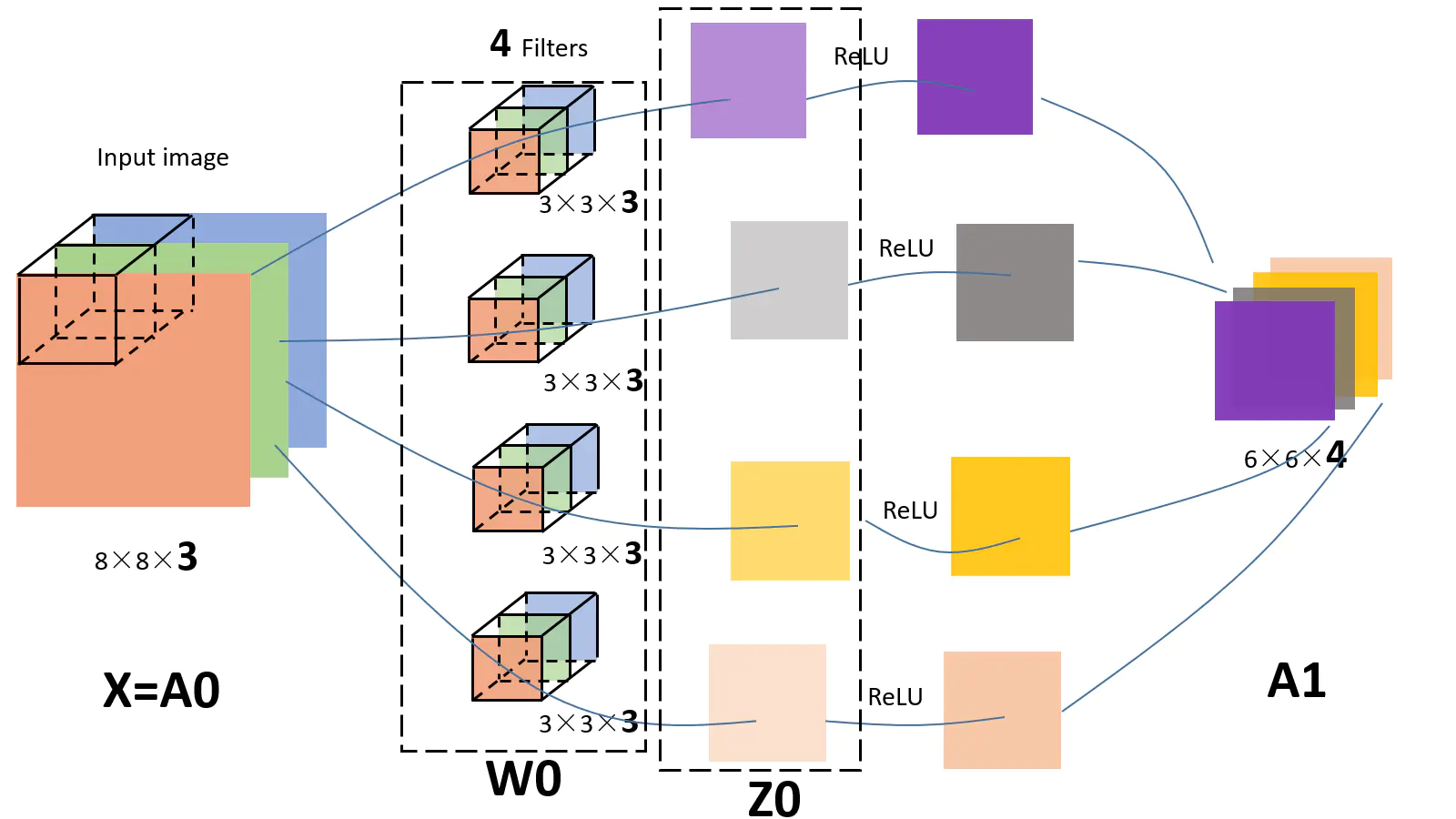
这里就有个特例, $1\times1$卷积. 它能够通过任意的卷积核数量在不改变特征图长和宽的情况下, 改变深度, 在Inception系列模型中, 大量的使用了这个技巧来控制信息.
步长 Stride
步长是每滑动一次所前进的距离, 也就是每次向前拖动多少个单位. 即$x’=x+p$.
填充 Padding
卷积一步步计算后, 会让图片越来越小. 但是我们可以在图片边缘补上一圈数据, 使得卷积能够继续运算. Tensorflow中有两种padding模式, 在Stride=1的情况下, SAME指的是在输入图片的边缘补0, 输出图像大小与原来是相同的, 并且$p=\frac{f-1}{2}$, 大小为VALID就是不补. VALID可能导致在某些情况下卷积运算的数据丢失. 输出图像为$(n-f+1)\times(n-f+1)$.
关于空间中的位置信息泄露是否来源于Padding, 这个一直都有争议.
参数计算
对于输入数据的大小$W_{in}\times H_{in}\times D_{in}$, 卷积核个数$K$, 卷积核大小$F$, 步长$S$, 填充$P$, 有输出:
$$
\displaylines{
W_{out}=H_{out}= \lfloor\frac{W_{in}-F+2P}{S}\rfloor+1 \\
D_{out}=K}
$$
该层卷积核的参数个数是(本层的卷积核体积+偏置)*本层卷积核个数:
$$
N=(F\times F\times D_{in} + 1)\times K
$$
池化层 Pooling Layer
池化层也叫下采样层, 其实也是一种滑动的操作, 池化层里没有需要训练的参数. 池化也分为最大池化和平均池化两种. 池化的步长和窗口大小相同, 这保证了每次池化时都能取到不相交的区域. 池化增大了每个元素单元对应的感受野, 更利于抽取更抽象而有效的特征, 减少了过拟合. 池化时, 池化操作发生在每个通道上, 而不是像CNN一样将各通道输入加在一起. 也就是说, 池化后的输出深度和输入深度相等.
平均池化层 AveragePooling
平均池化取的是窗口内所有元素的平均值. 平均池化在反向传播时, 将梯度平均分为$n$份, 平均分配到原来对应的位置上, 这样保持池化前后梯度之和不变.
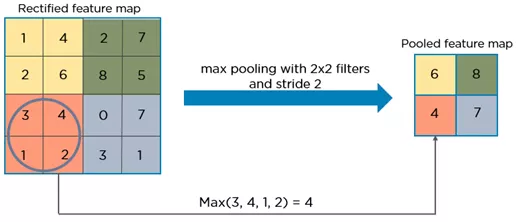
最大池化层 MaxPooling
最大池化层取的是窗口内所有元素的最大值. 有一更为极端的例子是全局最大池化层, 它将每一张特征图取最大值, 最终只得到一个值. 最大池化层在前向传播时会记录最大值的位置, 反向传播时只对对应位置的参数进行调整.
批量标准化层 Batch Normalization Layer
批量标准化能把输入直接强行拉到标准正态分布$\mathcal{N}(0, 1)$上, 并重新缩放平移, 使得激活函数输入值落在对输入相对来说敏感的区域, 由小的输入变化导致更大的梯度变化, 从而加快收敛速度. 如果不加BN, 输入分布会经常发生变化, 后续网络在学习时总会因为前面层的分布变化而变化, BN减少了层和层之间的耦合度.
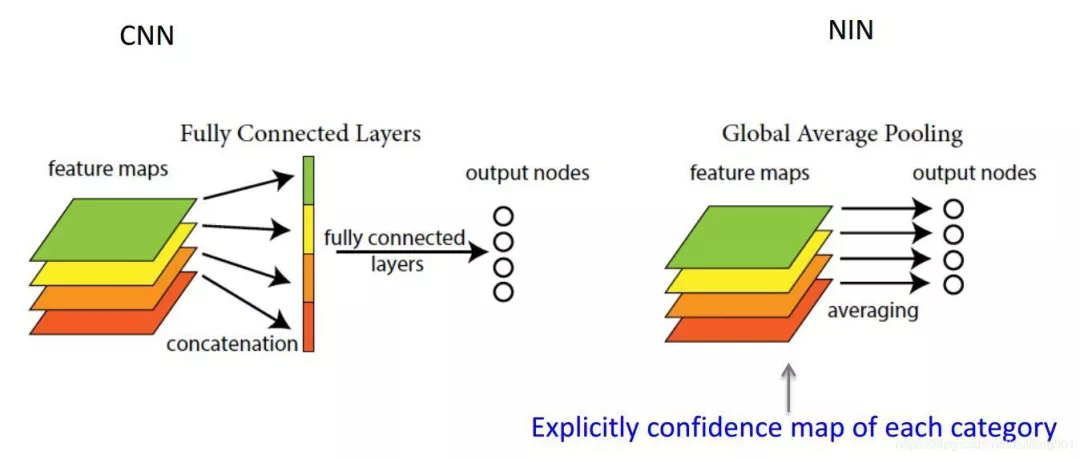
全连接层 Fully Connected Layer
FC层其实就是一层普通的神经网络, 它与上一层是全连接的. 用于分类所以激活函数为Softmax, 一般只用在最后一层或两层, 或预训练网络后添加的几层. 如果是在预训练网络后添加了几层FC进行调参, 那么这个预训练网络在做的事情也是特征抽取或特征提取, 它通过预训练的知识抽取了对事物的一般看法, 加上FC层后能够较好地完成我们指定的分类. 这种学习方式也叫作迁移学习(Transfer Learning). 但是过多的FC层会导致参数过多, 并且提高过拟合的可能性. 现在一般直接用全局最大池化层代替全连接层能够降低模型的参数, 并且表现稳定.

残差块 Residual Block
VGG在研究时候发现, 有时深度神经网络的层数越多, 起到的效果却不是很好. 这是因为在网络加深的过程中, 因为特征不断地被高度抽象, 导致最低阶时的原始特征已经被逐渐的消磨掉了. 假设已有一个最优化的18层网络结构, 当我们设计网络结构时, 假设设计了34层, 多出来的16层实际上是完全冗余的, 那么经过冗余层时的输入和输出实际上是和最优层的输入输出完全一致的. 那么实际模型训练的效果不一定能比最优化模型的效果好, 这称为退化问题. 理论上来说, 网络越深, 模型的表达能力越强. 如何在维持网络深度的情况下提升性能?
基于这个思想, 如果能通过某种方式实现低阶信息到高阶信息的直接传递, 应该可以在很深的神经网络的情况下, 达到很好的效果. 这种跳跃式的做法也可以形象的叫Shortcut connection, 一条捷径. 可以看到下述两个图中的信息传递都是跨层的. 我们把下述结构称为残差块:
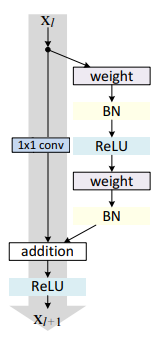
残差网络就是由一系列的残差块组成的. 残差块分为直接映射部分$h(x_l)$和残差部分$\mathcal{F}(x_l, W_l)$. 一般情况下在卷积神经网络中, 很有可能输入$x_l$和输出$x_{l+1}$的特征图尺寸不同, 这时候就必须要用$1\times 1$卷积核进行升维和降维, $h(x)$描述的就是这个升维和降维的过程. 映射中有多重方式, 但根据数学证明和事实证明直接映射是最好的选择, 效果最好.

它的数学表达:
$$
x_{l+1} = h(x_l) + \mathcal{F}(x_l,W_l)
$$
在上图中, 两层权重都是冗余的, 那么神经网络最终拟合的结果应该是函数$H(x)=x$这个恒等映射, 因为非线性映射导致直接学习恒等映射函数十分困难, 网络学习的肯定是不恒等映射. 如果将网络设计为$H(x)=F(x)+x$, 从而转化为学习一个残差函数$F(x)=H(x)-x$, 当$F(x)=0$时, 就能得到恒等映射函数, 对残差的拟合肯定更容易. 也就是说, 对于冗余层, 模型最差程度也能学习到和原来一样的结果.
除了解决了网络的退化问题, 还解决了梯度消失和梯度爆炸. 即使上图中的$\mathcal{F}(x)$的部分为0, 也仍然可以由直接加过来的$\mathcal x$. 进行良性的梯度传播, 而不至于因为连乘而导致梯度消失或爆炸.
点这里看ResNet论文和恒等映射起到作用的分析.

