评估指标 Metrics
混淆矩阵 Confusion Matrix
对于简单的二分类情况, 混淆矩阵就是如下形式:
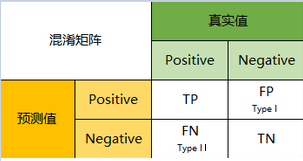
混淆矩阵把数据和模型预测情况分为四类:
真实值是positive, 模型认为是positive的数量(True Positive=TP)
真实值是positive, 模型认为是negative的数量(False Negative=FN):这就是统计学上的第二类错误(Type II Error).
真实值是negative, 模型认为是positive的数量(False Positive=FP):这就是统计学上的第一类错误(Type I Error).
真实值是negative, 模型认为是negative的数量(True Negative=TN).
一级指标
一级指标就是对于混淆矩阵来说的, 那肯定是处于对角线上的数字越大越好, 越大说明分类正确的越多. 因此混淆矩阵也常用热图进行绘制, 能够一眼看出分类情况.
二级指标
但是,混淆矩阵里面统计的是个数,有时候面对大量的数据,光凭算个数,很难衡量模型的优劣。因此混淆矩阵在基本的统计结果上又延伸了如下4个指标,我称他们是二级指标(通过最底层指标加减乘除得到的):
- 准确率(Accuracy) - 针对分类正确
- 精确率(Precision) - 所有阳性中分类正确的
- 灵敏度(Sensitivity) - 就是召回率(Recall), 也叫查全率.
- 特异度(Specificity)
| 指标 | 公式 | 含义 |
|---|---|---|
| 准确率 | $Accuracy= \frac{TP+TN}{TP+TN+FP+FN}$ | 所有分类正确的样本占样本总数的百分比. |
| 精度 | $Precision=\frac{TP}{TP+FP}$ | 所有预测阳性的样本中真实为阳性的百分比. |
| 召回率 | $Recall=\frac{TP}{TP+FN}$ | 所有真实阳性的结果中预测为阳性的百分比. |
| 特异度 | $Specificity=\frac{TN}{TN+FP}$ | 所有真实阴性的结果中预测为阴性的百分比. |
三级指标
三级指标主要是$F_1\ score$ 和 $F_\beta \ score$.
$$
F_1 \ score = 2 \cdot \frac{Precision \cdot Recall} {Precision + Recall}
$$
即$F_1 \ score$ 是 $Precision$ 和 $Recall$ 的调和平均数. 将这个情况扩展到一般情况, 称之为$F_\beta \ score$.
$$
F_\beta \ score = (1+N^2) \cdot \frac{Precision \cdot Recall}{N^2\cdot Precision + Recall} = \frac{Precision \cdot Recall}{\frac{N^2}{1+N^2}\cdot Precision + \frac{1}{1+N^2}Recall}
$$
$\beta$ 的取值范围是$[0, +\infty)$, 有以下特殊情况:
- ${\lim\limits_{N \to 0}}F_\beta \ score= Precision$
- $\beta = 1, F_\beta = F_1\ score$
- ${\lim\limits_{N \to +\infty}}F_\beta \ score= Recall$
- 能够从不同的$\beta$ 值看出, 如果$\beta$ 值越小, $Precision$ 越重要, 反之$\beta$ 值越大, $Recall$ 越重要.
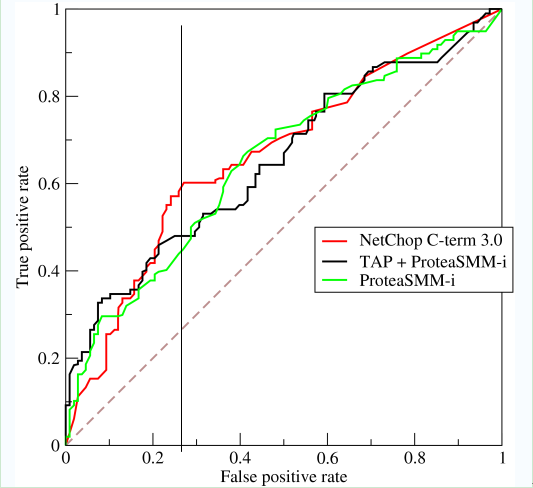
ROC曲线
ROC(Receiver Operating Characteristic) 受试者特性曲线. 纵坐标是true positive rate(TPR), 指的是所有实际为阳性的样本中被正确判定为阳性的比例. 横坐标是false positive rate(FPR), 指的是所有实际为阴性的样本中被错误判定为阳性的比例.
$$
\displaylines{
TPR = \frac{TP}{TP+FN} \\
FPR = \frac{FP}{FP+TN}
}
$$
曲线下方的面积成为AUC(Area Under roc Curve), 值通常在0.5到1之间, 认为面积越大的模型越好. 小于0.5的补救方法就是按照模型说的反着做.