Distilling the Knowledge in a Neural Network
本文是论文Distilling the Knowledge in a Neural Network的阅读笔记和个人理解.
Basic Idea
现有机器学习中, 任何算法都可以用Ensemble的方法来提升性能, 但这样做会花费昂贵的计算资源, 并且不利于部署到真实场景中.
作者尝试提出一种把大模型知识尽可能的压缩进单个小模型的方法.
Distillation
人们希望得到的模型并不是在单一的数据集上拟合完美, 而是要求模型具有强大的泛化能力. 在某个问题的某个具体数据及上, 通常训练出的模型与真实问题会存在偏差, 存在一点点过拟合.
那么对于一个有能力的大模型, 就有希望直接利用大模型的知识, 训练一个具有更强泛化能力的小模型, 让小模型直接学习大模型的泛化能力.
从泛化能力的角度来考虑, 知识蒸馏非常像一种正则化手段.
训练时经常所采用的标签是独热编码, Softmax会刻意放大Logits之间的差距. 这使得模型输出的类别概率在某一类是非常大的(文中也称为Hard Target), 其他类别的概率都非常小.
但不同类别之间的相对概率仍然很重要, 例如猫的图片可能与狗有一定相似, 它一定比和苹果的相似性要低. 这种类别概率差异仍然可能存在着一些隐含的知识, 但它会被Softmax所抹除掉, 所以需要一些手段把这种知识传授给小模型.
一种可以尝试的方法是把大模型(Teacher)的预测结果和大模型的知识作为小模型(Student)的Target, 即将处理过后的大模型Logits作为Label或Label的一部分训练小模型.
既然是Softmax抹除了不同类别之间的差异, 那么可以对Softmax改动, 弱化其对隐含知识的影响.
假设神经网络在没有经过Softmax前的Logits记为$z_i$, 我们可以添加”温度“$T$ 来弱化影响, 记结果为$q_i$:
$$
q_{i}=\frac{\exp \left(z_{i}\right)}{\sum_{j} \exp \left(z_{j}\right)} \quad \rightarrow \quad q_{i}=\frac{\exp \left(z_{i} / T\right)}{\sum_{j} \exp \left(z_{j} / T\right)}
$$
$T=1$ 时, 就是正常的Softmax. 当$T > 1$ 时, 原来的Softmax将变得更加软化, 不同类别之间的差距, 不再显得类别间的差距那么绝对. Teacher中的不同类别之间的暗含知识得到一定保留. 因为标签变得软化了, 所以熵更大, 也保存了更多的信息.
如果这个式子不够直观体现出它的作用, 我做出了不同$T$ 对Target $q_i$ 的影响变化曲线图:
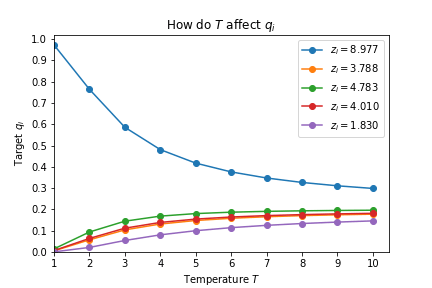
随着$T$ 的增大, 生成的Soft Target之间的差距会越来越小, 变得Softer.
Student将使用Hard Target和Soft Target共同训练自己, Teacher软化后的知识将作为损失函数的一部分调节Student的参数:
$$
\mathcal{L} = \mathcal{L}_{hard} + \lambda \mathcal{L}_{soft}
$$
$\lambda$ 为超参, 用于调节Teacher Soft Target的影响占比. 具体来说, Student应以常温$T=1$ 用Hard Target训练自己, 即损失的第一项. 同时, Teacher和Student的蒸馏时应对Softmax加以高温$T$, 即损失的第二项, 蒸馏过程的示意图如下:
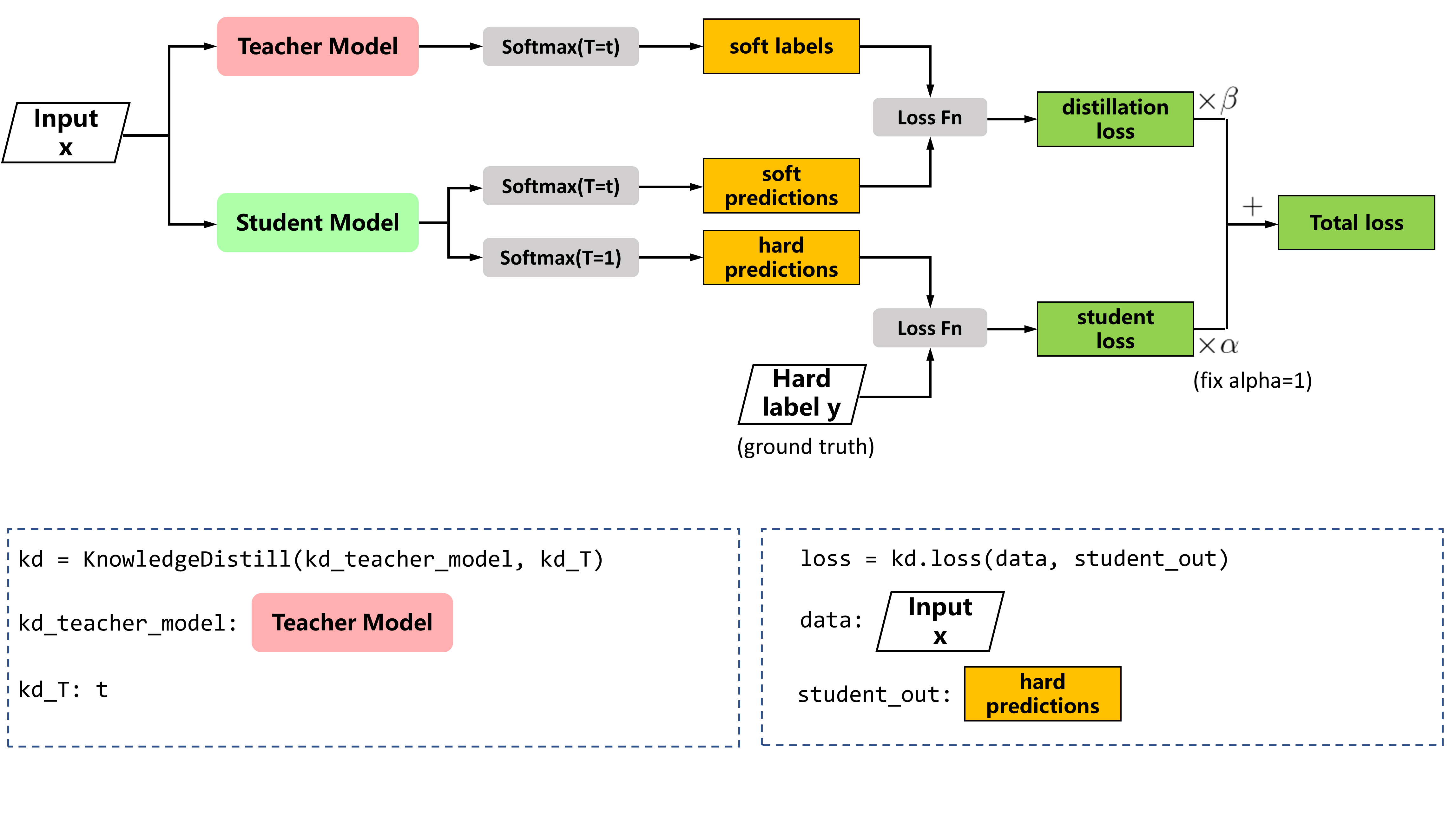
在训练时, 必须保证Teacher和Student的温度一致, 当训练完成后, Student预测不再使用$T$, 或者说训练完成后的推断设置$T=1$.
同时, 由于温度$T$ 的影响, 梯度均缩小了$T^2$ 倍(详见下一小节最后), 所以在设置$\lambda$ 时, 需要让其尽可能大一些, 或者乘$T^2$ 倍, 才能保证两种损失的贡献度相同.
Matching Logits is a Special Case of Distillation
作者下面证明了直接让Student学Teacher的Logits只是蒸馏的一种特殊情况.
下面涉及到更详细的推导过程在末尾引文连接已附上.
假设我们处理的问题所采用的损失函数是交叉熵$C$, 梯度为$\frac{\partial C}{\partial z_i}$, Teacher模型的Logits为$v_i$, 以及其对应的概率为$p_i$, 则有:
$$
\frac{\partial C}{\partial z_{i}}=\frac{1}{T}\left(q_{i}-p_{i}\right)=\frac{1}{T}\left(\frac{e^{z_{i} / T}}{\sum_{j} e^{z_{j} / T}}-\frac{e^{v_{i} / T}}{\sum_{j} e^{v_{j} / T}}\right)
$$
当$T$ 相较于Logits充分大的时候, 可以使用泰勒展开, 有$e^{x/T}\approx1+x/T$:
$$
\frac{\partial C}{\partial z_{i}} \approx \frac{1}{T}\left(\frac{1+z_{i} / T}{N+\sum_{j} z_{j} / T}-\frac{1+v_{i} / T}{N+\sum_{j} v_{j} / T}\right)
$$
当对Logits做了零均值假设后, 有$\sum_jz_j=\sum_jv_j=0$, 结合上式有:
$$
\frac{\partial C}{\partial z_{i}} \approx \frac{1}{N T^{2}}\left(z_{i}-v_{i}\right)
$$
因此, 在较高的温度$T$ 设置下, 蒸馏等价于最小化$\frac{1}{2}(z_i - v_i)^2$, 也就是直接把Teacher和Student的Logits匹配, 所以匹配Logits是一种蒸馏的特殊情况.
当温度较低时, 对负样本的关注就比较少, 可能滤去关键信息, 但实际上这有利有弊. 有些负样本的Logits应该是非常小的负值, 这种极小的负值在高温时的作用会被放大, 作为强大的噪声影响Student. 在低温时, 这种噪声将被滤去.
所以温度的选取一般依赖于经验, 不要太高也不要太低.
分母上有$T^2$, 所以在知识蒸馏时, $\mathcal{L}_{soft}$ 的影响被缩小了$T^2$, 所以需要在设置损失项时平衡回来.
Experiments
MNIST
作者将知识蒸馏应用于小规模数据集MNIST, Teacher训练了一个两隐层的DNN并使用Dropout和Weight Constraints, Student网络也是两隐层的DNN但神经元个数比Teacher少, 不使用正则化手段.
作者尝试了几种不同的小模型设置, 在合适的温度下取得了与Teacher相近的表现.
Speech Recognition
语音识别中, 当时比较流行的做法是用HMM, 并按照如下目标优化模型参数$\theta$:
$$
\boldsymbol{\theta}=\arg \max _{\boldsymbol{\theta}^{\prime}} P\left(h_{t} \mid \mathbf{s}_{t} ; \boldsymbol{\theta}^{\prime}\right)
$$
其中$\mathbf{s_t}$ 为$t$ 时刻的结果, $h_t$ 为$t$ 时刻的HMM隐态.
结果如下:
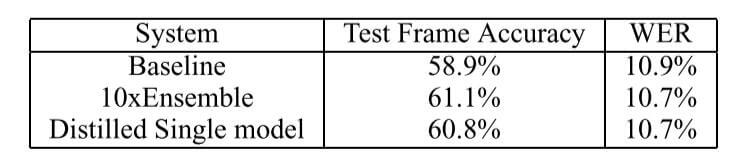
蒸馏一个小模型出来后的结果比单独Train一个大模型的效果要好.
JFT
JFT是一个比前面二者大得多的图像分类数据集, 这个数据集有1亿张图片, 15000个类别.
作者训练了一个通用模型和若干个专家模型, 作为没有使用知识蒸馏时的Baseline.
对若干种通用模型经常易混淆的类做一个聚类(也有可能有些类不被归纳进专家模型, 这就需要通用模型自己处理), 记为$S^m$, 作为多个JFT的子集, 将不同子集的数据交给不同的专家模型$m$ 预测, 下面是作者展示出的子集示例:

对于输入的图片$\mathbf{x}$, 得到分类结果需要两步:
- 粗分: 对于每个测试数据, 由通用模型得到$n$ 个最有可能的类别, 记这些类为$k$.
- 细分: 按照$k$, $S^m$ 的非空交集找到相应的专家模型$A_k$ , 让专家模型进行预测.
专家模型极易过拟合. 为了防止过拟合, 专家模型所采用的一半数据来自指定类别, 剩下一半来自全数据集, 其他类别被全部设置为一个单独的”Dustbin”类.
然后最小化所有类别的概率分布$\mathbf{q}$ 和通用模型, 专家模型得到的概率分布的KL散度.
KL散度(也称为相对熵)常用于度量两个分布之间的差异性, 假设$P$ 为样本真实分布, $Q$ 为模型预测的分布, 根据KL散度有:
$$
D_{\mathrm{KL}}(P \| Q)=\mathbb{E}_{\mathrm{x} \sim P}\left[\log \frac{P(x)}{Q(x)}\right]=\mathbb{E}_{\mathrm{x} \sim P}[\log P(x)-\log Q(x)]
$$
当$P, Q$ 越接近时, $D_{\mathrm{KL}}(P \| Q)$ 就越小, 当$P, Q$ 分布完全相同时, $D_{\mathrm{KL}}(P \| Q)$ 为0.KL散度还有两个性质:
- 非负: KL散度是非负的.
- 不对称: 通常情况下, $D_{\mathrm{KL}}(P \| Q) \neq D_{\mathrm{KL}}(Q \| P)$, KL散度并不是真正意义上的距离.
记通用模型得到的概率分布为$\mathbf{p}^g$, 专家模型得到的概率分布为$\mathbf{p}^m$, 总体分布$\mathbf{q}$ 和模型预测得到概率分布的KL散度计算方式如下:
$$
K L\left(\mathbf{p}^{g}, \mathbf{q}\right)+\sum_{m \in A_{k}} K L\left(\mathbf{p}^{m}, \mathbf{q}\right)
$$
总体来说, 最好的结果如下:

当时JFT的Baseline是CNN.
逐渐增大专家模型的数量, 结果如下:
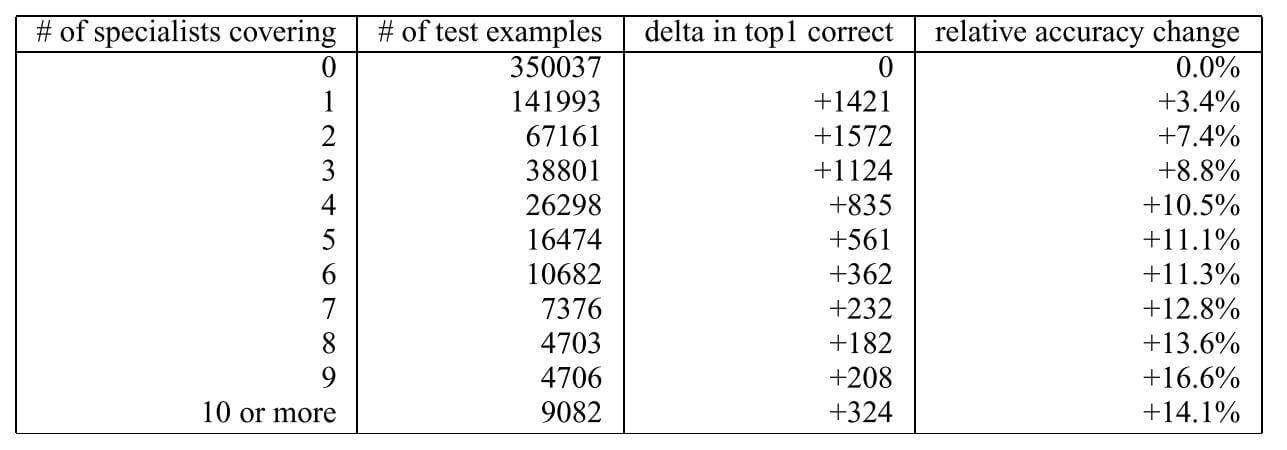
随专家数量提升, 相对提升逐渐增大.
前面说过, 专家模型极易过拟合, 如果使用3%的数据的Hard Target训练专家模型, 它更有可能过拟合, 并且在附加早停的情况下非常早就停止了.
但如果使用知识蒸馏, 把Hard Target用Soft Target代替, 仅用3%的数据训练专家模型, 不但不会很早早停, 而且还能保留专家模型的泛化能力, 效果如下:

使用Soft Target效果要好于同样使用3%的数据的Baseline的训练效果, 并且与使用全部数据的Baseline效果相近.
Recommended
- 论文原文: Distilling the Knowledge in a Neural Network
- 比较全面的文章: 【经典简读】知识蒸馏(Knowledge Distillation) 经典之作
- BERT相关:深度神经网络模型蒸馏Distillation
- 很详细的视频(需翻墙): Hinton:distilling knowledge in a neural network
- 数学推导(推荐看看): Distilling the Knowledge in a Neural Network 理论推导
Summary
知识蒸馏是一种将大模型的隐含知识通过某种手段提取出来, 提炼传授给小模型的模型压缩方法.
该论文发表自2014年, 当时深度学习的模型还没有发展到像现在这样的超大规模, Hinton能提出这种具有工程意义并且值得挖掘的新方向相当有远见.
蒸馏为何有效, 人们还没有彻底摸清其中的作用原理.
甚至单个模型的自蒸馏也是有效的… 这点非常诡异, 为什么模型单单依靠样本本身却无法达到自蒸馏后的效果? 样本之间隐含的差异居然需要自己产生的产物重新喂给自己才能吸收(反刍)?
读完本论文后, 自然会产生进一步的想法. 直接把Logits蒸给小模型效果如何? 能蒸Logits为什么不直接蒸Feature呢? 要是蒸Feature也不够直接的话把参数蒸给小模型是不是也可以? 这些想法确实都可以, 或多或少都有效果.

