损失函数 Loss function
损失函数是用来度量模型当前预测状况与损失目标的差距的函数.
均方误差 MSE
也称为平方损失, L2损失, 均方误差(Mean Squared error). 有时候人们也直接将其开根号称为RMSE, 这样能更好的反映出模型和真实值之间的差异, 以至于不像MSE看起来的那么大. 有时候分母上多挂个2是为了求导方便.
$$
MSE = \frac{\sum\limits_{i=1}^n(y_i-\hat{y_i})^2}{n}
$$
平均绝对值误差 MAE
平均绝对值误差(Mean Absolute Error) 也称之为L1损失, 是另一种损失函数, 它表示预测值的平均误差幅度而不考虑误差的方向.
$$
MAE = \frac{\sum \limits_{i=1}^n \left| y_i-\hat{y_i}\right|}{n}
$$
当训练数据中含有较多的异常值时MAE更为有效. 当我们对所有观测值进行处理时, 如果利用MSE进行优化则我们会得到所有观测的均值, 而使用MAE则能得到所有观测的中值. 与均值相比, 中值对于异常值的鲁棒性更好, 这就意味着平均绝对误差对于异常值有着比均方误差更好的鲁棒性. 但是MAE它的梯度在极值点处会有很大的跃变, 所以不利于梯度下降相关算法. MSE却能很好的收敛.
R2 score
$R^2\ score$ 也称为决定系数, 越大越好, 解决了不同量纲下模型的效果好坏.
$$
R^2 \ score = 1 - \frac{\sum \limits_{i=1}^n (y_i-\hat{y_i})^2}{\sum \limits_{i=1}^n (y_i-\bar{y_i})^2} = 1 - \frac{\sum \limits_{i=1}^n (y_i-\hat{y_i})^2 / n}{\sum \limits_{i=1}^n (y_i-\bar{y_i})^2/ n} = 1 - \frac{MSE}{Var}
$$
第二项的分子代表我们实际作出的回归曲线和真实值之间的均方误差, 分母代表了在所有样本中取平均所获得的均方误差, 回归曲线越好, 那么二者之间的比值就越小, $R^2\ score$也就越趋近于1.
交叉熵 Cross Entropy
其实大多数情况下, 在分类问题中使用的损失函数是交叉熵. 很明显上述几种损失函数对于一个分类问题来说, 都不是好的损失函数. 而交叉熵从信息的角度, 从概率入手, 很好的衡量模型的损失. 熵本身就是系统混乱度的度量, 熵越大, 则代表信息的不确定性越大. 在这里, 熵越大, 则代表模型预测的结果越差, 也就是损失值越大. 因为伴随着概率, 所以二分类交叉熵经常伴随sigmoid, 多分类伴随softmax, 这两个函数能将神经网络的输出映射到概率范围内.
二分类交叉熵
假设$y_i$是预测样本$i$的实际概率(或者说标签), $p_i$是第$i$个样本的类别预测概率, 则有:
$$
Entropy = -\sum^m_{i=1}\left[y_i\log{(1-p_i)} + (1-y_i)\log {p_i}\right]
$$
加入负号是为了保证熵为正, 能够让它的规律符合损失函数定义.
多分类交叉熵
多分类就是将二分类扩展到一般情况. 共有$m$个类, $n$个样本, $y_{ij}$是第$i$个样本对应第$j$个类别的标签, $p_{ij}$是第$i$个样本对应第$j$个类别的预测概率.
$$
Entropy = -\sum^n_{i=1}\sum^m_{j=1}y_{ij}\log {p_{ij}}
$$
正则化 Regularization
正则化也可以看做是损失函数的惩罚项. 正则化是对模型优化方向加以限制, 在损失函数后面添加的项. 这样在计算损失函数时, 也会将人为优化的方向考虑进去. 如果模型没有朝着人们想要的方向发展, 会导致损失很高, 模型则不会向着该方向更新. 对于原来的损失函数$E(w; X, y)$ 和仅与权重相关的正则项$\Omega(w)$, 正则项超参数$\alpha$, 新的损失函数$E_r(w; X, y)$:
$$
E_r(w; X, y)=E(w; X, y) + \alpha\Omega(w)
$$
L1正则化 L1 Regularization
使用L1正则化的模型也叫作Lasso回归模型. L1正则化是将模型权重的个向量绝对值之和加到一起. 这样模型自动的将不重要的特征系数变小, 逐渐趋于0. 因此L1正则化可以产生稀疏权值矩阵, 即产生一个稀疏模型, 用于特征选择.
$$
\Omega(w)=\sum_i^W|w_i|
$$
相比于后面提到的L2正则化来说, L1具有更好的鲁棒性, 当出现异常值时, 异常值不会被放大. 但L1因为含有绝对值, 非常难以计算.
L1正则化为什么易于产生稀疏解?
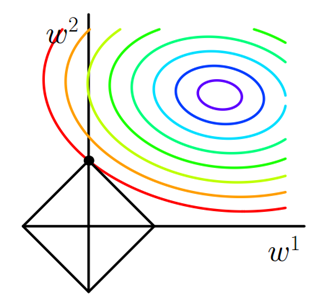
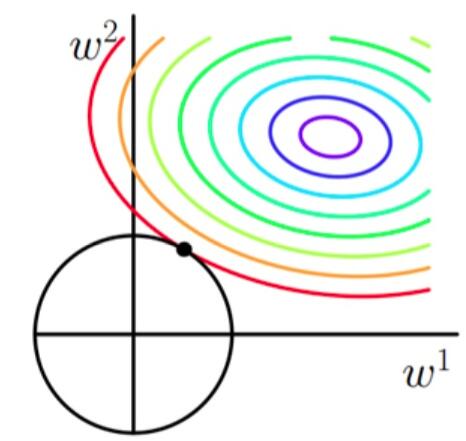
在寻找最优解时, L1正则由于是权重的绝对值, 做出的图像如图中的正方形所示, 更容易在某方向权重为0时找到解, 所以能够将整个权重矩阵稀疏化.而且L1的导数因带有绝对值而容易发生突变, 所以在0处时取到极小值的几率很大. 或者说L1因为涉及绝对值, 如果想最小化惩罚, 就是让对应的$w_i$取0.
L2正则化 L2 Regularization
使用L2正则化的模型也叫作Ridge回归模型(岭回归模型). L2具有更均匀的输出. 也非常便于计算.
$$
\Omega(w)=\sum_i^Ww_i^2
$$
当模型权重过多, 或者某个权重向量值过大时, 都会得到严厉的惩罚. 但是因为L2是权重的平方, 因此当模型遇到异常值时, 对权重进行大幅度调整, 这个误差会被放大.